二分+ST表+递推,Cf 1237D - Balanced Playlist
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
Problem - 1237D - Codeforces
二、解题报告
1、思路分析
case3提示我们一件事情:如果存在某个位置永远不停止,那么所有位置都满足永远不停止
很容易证明
随着下标右移,区间最大值不会变大,那么后面2倍大于旧的最大值的数的二倍仍然大于新的最大值
那么对于每个位置我们要找到第一个满足a[i] < max / 2的 i
我们可以st表预处理出区间最大值最小值
然后对于递推求解ans
对于i,我们二分查找找到第一个大于a[i]的j,同样二分查找找到第一个a[k] < a[i]的k
如果k < j,那么显然答案就是j - i
否则, ans[i] = k - i + ans[k % N]
我们建立了递推关系,一共N个状态,每个状态O(log)转移,总体时间复杂度就是O(NlogN)
2、复杂度
时间复杂度: O(NlogN)空间复杂度:O(NlogN)
3、代码详解
#include <bits/stdc++.h>
using i64 = long long;
using i128 = __int128;
using PII = std::pair<int, int>;std::ostream& operator<< (std::ostream& out, i128 x) {std::string s;while (x) s += ((x % 10) ^ 48), x /= 10;std::reverse(s.begin(), s.end());return out << s;
}template<class T, int M>
struct ST {T n;std::vector<T> nums;std::vector<T> log2;std::vector<std::array<T, M>> f0, f1;ST (T _n, std::vector<T>& _nums): n(_n), nums(_nums), log2(_n + 1), f0(_n), f1(_n) {log2[2] = 1;for (int i = 3; i <= n; i ++ ) log2[i] = log2[i >> 1] + 1;for (int i = 0; i < n; i ++ ) f0[i][0] = f1[i][0] = nums[i];for (int j = 1; j < M; j ++ )for (int i = 0; i < n && i + (1 << (j - 1)) < n; i ++ )f0[i][j] = std::max(f0[i][j - 1], f0[i + (1 << (j - 1))][j - 1]), f1[i][j] = std::min(f1[i][j - 1], f1[i + (1 << (j - 1))][j - 1]);}std::array<T, 2> query(int l, int r) {int k = log2[r - l + 1];return { std::max(f0[l][k], f0[r - (1 << k) + 1][k]), std::min(f1[l][k], f1[r - (1 << k) + 1][k]) };}
};void solve() {int N;std::cin >> N;std::vector<int> a(N * 2);for (int i = 0; i < N; i ++ ) std::cin >> a[i], a[i + N] = a[i];ST<int, 18> st(N * 2, a);if (st.query(0, N - 1)[0] <= st.query(0, N - 1)[1] * 2LL) {for (int i = 0; i < N; i ++ ) std::cout << -1 << " \n"[i == N - 1];return;}std::vector<int> ans(N, -1);auto findmi = [&](int l, int r) -> int {int x = a[l - 1];while (l < r) {int mid = l + r >> 1;auto [ma, mi] = st.query(l, mid);if (mi * 2LL < x) r = mid;else l = mid + 1;}return l;};auto findma = [&](int l, int r) -> int {int x = a[l - 1];while (l < r) {int mid = l + r >> 1;auto [ma, mi] = st.query(l, mid);if (ma > x) r = mid;else l = mid + 1;} return l;};auto dfs = [&](auto&& self, int x) -> int {if (~ans[x]) return ans[x];int lt = findmi(x + 1, x + N), gt = findma(x + 1, x + N);if (lt < gt) return ans[x] = lt - x;return ans[x] = gt - x + self(self, gt % N);};for (int i = 0; i < N; i ++ ) std::cout << dfs(dfs, i) << " \n"[i == N - 1];
} int main(int argc, char** argv) {std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);int _ = 1;// std::cin >> _;while (_ --)solve();return 0;
}相关文章:

二分+ST表+递推,Cf 1237D - Balanced Playlist
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 Problem - 1237D - Codeforces 二、解题报告 1、思路分析 case3提示我们一件事情:如果存在某个位置永远不停止,那么所有位置都满足永远不停止 很容易证明 随着下标右移,…...

被裁员不可怕,可怕的是你只会写代码!
“听说隔壁部门又要裁员了,人心惶惶的……” “是啊,这年头,工作真是越来越难了,谁知道下一个会不会是自己呢?” 这两天,公司里弥漫着一股紧张的气氛,裁员的消息,就像是一场突如其来…...

服务器之间的时间如何保证一致
服务器之间的时间一致性主要通过以下几种方法和技术来保证: NTP(Network Time Protocol)同步:这是最常见的时钟同步方法。NTP协议允许服务器从一个或多个时间服务器(称为NTP服务器)获取精确的时间信息&…...
算法体系-20 第二十节暴力递归到动态规划
前言 动态规划模型从尝试暴力递归到傻缓存到动态规划 四种模型和体系班两种模型一共六种模型 0.1 从左往右模型 0.2 范围讨论模型范围尝试模型 (这种模型特别在乎讨论开头如何如何 结尾如何如何) 玩家博弈问题,玩家玩纸牌只能那左或者右 0.3 …...
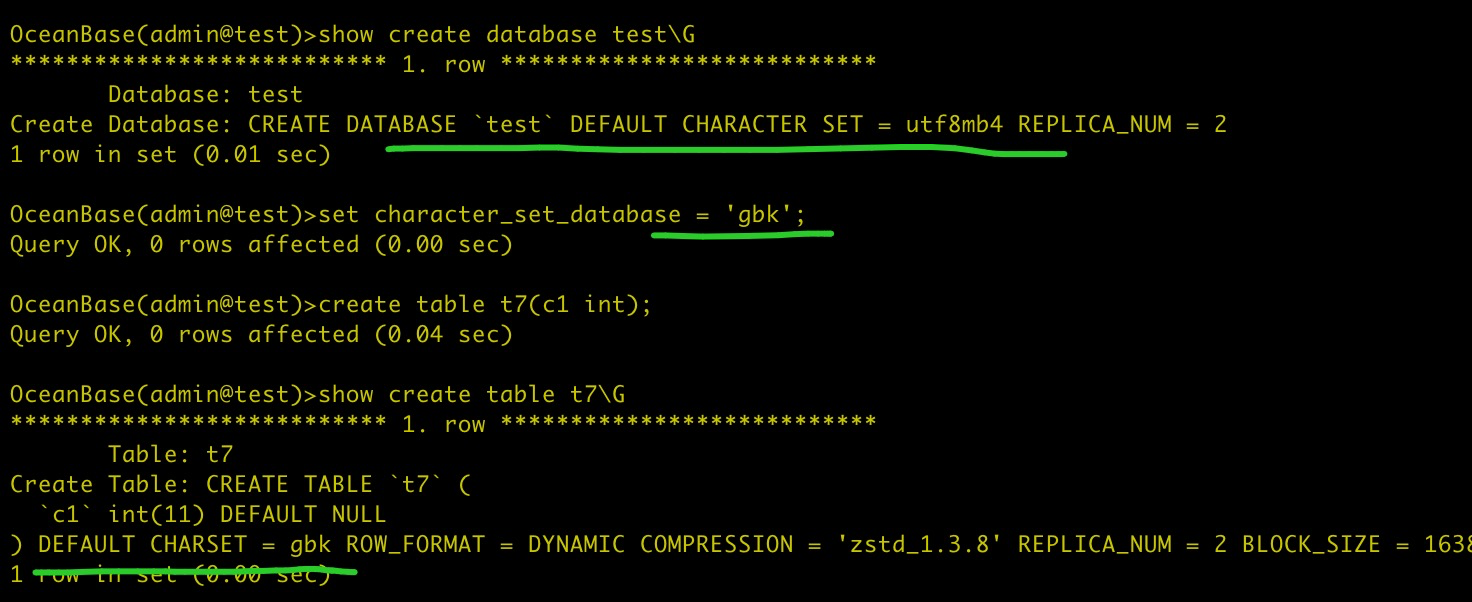
字符集相关变量理解
建表 创建一个新表,想让他的字符集是 gbk,怎么弄? 尝试1: 失败!原因: set names gbk; 等价于:set character_set_client gbk; set character_set_connection gbk; set character_set_results gbk;尝…...

618哪些数码产品比较好?2024超高人气产品推荐!
随着6.18大促的脚步渐近,你是否已经按捺不住内心的激动,想要在网络购物的海洋中畅游,尽情享受购物的狂欢?然而,面对繁多的商品和各式各样的优惠活动,你是否感到了一丝迷茫?作为一位经验丰富的网…...

基础-01-计算机网络概论
一. 计算机网络的发展与分类 1.计算机网络的形成与发展 计算机网络:计算机技术与通信技术的结合 ICTITCT 2.计算机网络标准阶段 3.计算机网络分类1:通信子网和资源子网 通信子网:通信节点(集线器、交换机、路由器等)和通信链路(电话线、同轴电缆、无线电线路、卫…...
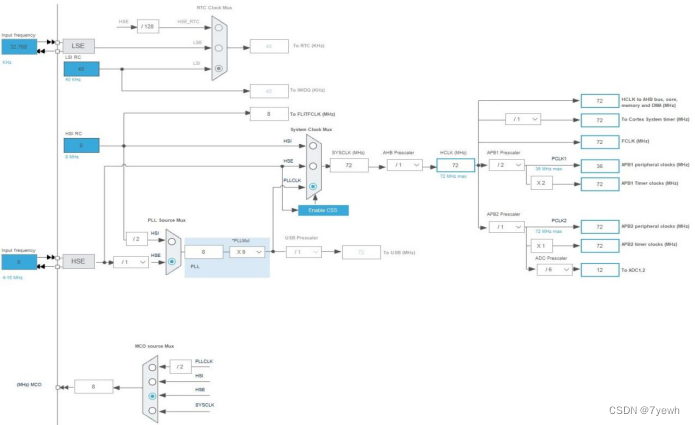
STM32学习笔记(一)--时钟树详解
(1)时钟概述;时钟是具有周期性的脉冲信号,最常用的是占空比50%的方波。(时钟相当于单片机的脉搏;STM32本身非常复杂,外设非常的多,为了保持低功耗工作,STM32 的主控默认不…...
JAVA小知识16:JAVA常用的API
一、Math 方法名说明public static int abs(int a)获取参数绝对值public static double ceil(double a)向上取整public static double floor(double a)向下取整public static int round(float a)四舍五入public static int max(int a,int b)获取两个int值中的较大值public s…...

PaddleDetection快速体验quick_start
1 快速体验 # 设置显卡 export CUDA_VISIBLE_DEVICES0# 用PP-YOLO算法在COCO数据集上预训练模型预测一张图片 python tools/infer.py -c configs/ppyolo/ppyolo_r50vd_dcn_1x_coco.yml -o use_gputrue weightshttps://paddledet.bj.bcebos.com/models/ppyolo_r50vd_dcn_1x_coc…...

《Foundation CSS 参考手册》
《Foundation CSS 参考手册》 引言 Foundation 是一个强大的前端框架,它为开发者提供了一系列的CSS工具和组件,以便快速构建响应式、移动优先的网站。本参考手册旨在为那些希望深入了解和使用Foundation CSS的开发者提供一个全面的指南。 基础知识 1…...

方法递归-结合案例阶乘问题、求和问题和猴子吃桃问题
方法递归 递归是一种算法 在程序设计语言中广泛应用. 从形式上来说:方法调用自身的形式称为方法递归(recursion). 递归的形式: 直接递归:方法调用自己。间接递归:方法调用其他方法,其他方法…...
有一个主域名跟多个二级子域名时该怎么申请SSL证书?
当您拥有主域名以及多个子域名时,选择合适的SSL证书类型对于确保网站的安全性至关重要。以下是三种SSL证书类型的简要介绍: 单域名SSL证书: 功能:只能绑定单个域名,无论是主域名还是子域名。 适用场景:仅…...

LabVIEW伺服电机可应用在哪些领域
LabVIEW与伺服电机的结合,得益于LabVIEW强大的图形编程能力和伺服电机的高精度、高响应速度,广泛应用于多个领域。以下是一些主要应用领域: 1. 工业自动化 数控机床控制 LabVIEW用于控制伺服电机在数控机床中的运动,实现高精度的…...

nvidia 显卡 没有正确安装或配置 OpenGL 库
看到这个错误可能意味着你的系统没有正确安装或配置 OpenGL 库。以下是一些步骤来解决这个问题: 1. 安装必要的软件包 确保你已经安装了必要的软件包,包括 mesa-utils 和 nvidia-driver。 安装 mesa-utils sudo apt update sudo apt install mesa-ut…...
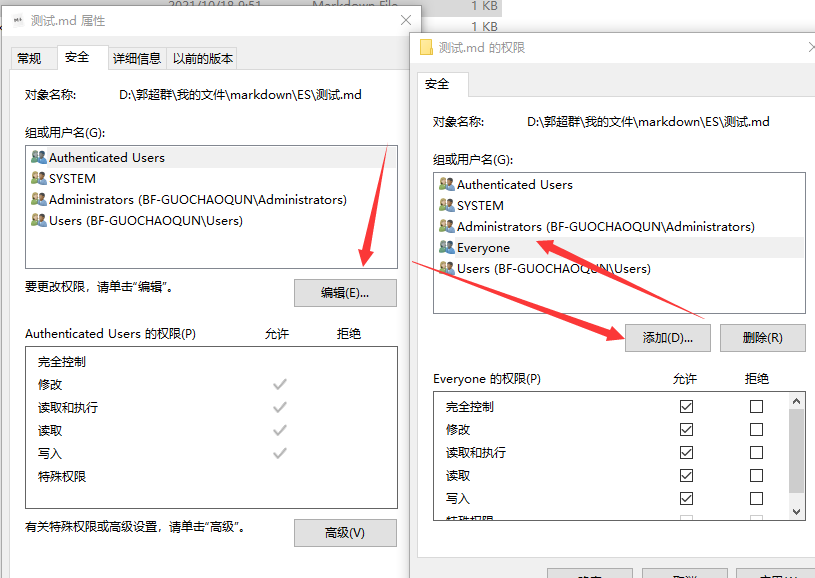
将自己md文件发布到自己的博客园实现文件的持久化存储
上传markdown文件到博客园 目录 【0】需求原因【1】功能【2】环境【最佳实践测试】 (1)查看 Typora 设置(2)配置 pycnblog 配置文件 config.yaml(3)运行 pycnblog 中的文件 cnblog_markdown.cmd࿰…...
)
uni-app的生命周期(应用,页面生命周期)
1. uni-app的生命周期(应用,页面生命周期) 1.1. 应用生命周期 1.1.1. 定义在app.vue中 生命周期函数名说明onLaunch当uni-app 初始化完成时触发(全局只触发一次)onShow当 uni-app 启动,或从后台进入前台…...

响应式企业网站建站系统源码 模版丰富+一站式建站 全开源可二次开发 带源码包+搭建部署教程
系统概述 在数字化转型的浪潮中,企业官网作为品牌展示、产品推广及客户服务的重要窗口,其建设质量直接影响着企业的线上形象与市场竞争力。响应式企业网站建站系统源码的出现,为企业提供了一种高效、灵活且成本可控的建站解决方案。 代码示…...

如何解除内存卡的写保护并格式化为exFAT文件系统
最近有客户提问内存卡提示写保护,且无法格式化为exFAT格式的问题,可能是由于多种原因引起的。以下是一些可能的解决方法: 1. 检查物理写保护开关 一些SD卡和MicroSD卡适配器上有一个小的物理开关,可以启用或禁用写保护。确保这个…...

【 EI会议 | 西南大学主办 | 往届均已实现检索】第三届神经形态计算国际会议(ICNC 2024)
第三届神经形态计算国际会议(ICNC 2024) 2024 3rd International Conference on Neuromorphic Computing (ICNC 2024) 一、重要信息 大会官网:www.ic-nc.org(点击投稿/参会/了解会议详情) 会议时间:2024年12月13-15…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...


