机器学习——集成学习和梯度提升决策树
集成学习
不同的算法都可以对解决同一个问题,但是可能准确率不同,集成学习就是不同算法按照某种组合来解决问题,使得准确率提升。
那怎么组合算法呢?
自举聚合算法**(bagging)**
顾名思义是 自举+聚合
自举是指的是自举采样,保证随机性,允许重复的又放回抽样,每次抽与原样本大小相同的样本出来,如果进行B次。则有B个数据集,然后独立的训练出模型 f(x),求得平均值
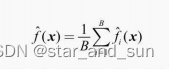
对于低偏差、高方差模型的稳定性有较大提升
随机森林
bagging算法的改进版就是随机森林

from tqdm import tqdm
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.model_selection import train_test_split# 创建随机数据集
X, y = make_classification(n_samples=1000, # 数据集大小n_features=16, # 特征数,即数据维度n_informative=5, # 有效特征个数n_redundant=2, # 冗余特征个数,为有效特征的随机线性组合n_classes=2, # 类别数flip_y=0.1, # 类别随机的样本个数,该值越大,分类越困难random_state=0 # 随机种子
)print(X.shape)
#%%
class RandomForest():def __init__(self, n_trees=10, max_features='sqrt'):# max_features是DTC的参数,表示结点分裂时随机采样的特征个数# sqrt代表取全部特征的平方根,None代表取全部特征,log2代表取全部特征的对数self.n_trees = n_treesself.oob_score = 0self.trees = [DTC(max_features=max_features)for _ in range(n_trees)]# 用X和y训练模型def fit(self, X, y):n_samples, n_features = X.shapeself.n_classes = np.unique(y).shape[0] # 集成模型的预测,累加单个模型预测的分类概率,再取较大值作为最终分类ensemble = np.zeros((n_samples, self.n_classes))for tree in self.trees:# 自举采样,该采样允许重复idx = np.random.randint(0, n_samples, n_samples)# 没有被采到的样本unsampled_mask = np.bincount(idx, minlength=n_samples) == 0unsampled_idx = np.arange(n_samples)[unsampled_mask]# 训练当前决策树tree.fit(X[idx], y[idx])# 累加决策树对OOB样本的预测ensemble[unsampled_idx] += tree.predict_proba(X[unsampled_idx])# 计算OOB分数,由于是分类任务,我们用正确率来衡量self.oob_score = np.mean(y == np.argmax(ensemble, axis=1))# 预测类别def predict(self, X):proba = self.predict_proba(X)return np.argmax(proba, axis=1)def predict_proba(self, X):# 取所有决策树预测概率的平均ensemble = np.mean([tree.predict_proba(X)for tree in self.trees], axis=0)return ensemble# 计算正确率def score(self, X, y):return np.mean(y == self.predict(X))
#%%
# 算法测试与可视化
num_trees = np.arange(1, 101, 5)
np.random.seed(0)
plt.figure()# bagging算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:for n_tree in pbar:rf = RandomForest(n_trees=n_tree, max_features=None)rf.fit(X, y)train_score.append(rf.score(X, y))oob_score.append(rf.oob_score)pbar.set_postfix({'n_tree': n_tree, 'train_score': train_score[-1], 'oob_score': oob_score[-1]})
plt.plot(num_trees, train_score, color='blue', label='bagging_train_score')
plt.plot(num_trees, oob_score, color='blue', linestyle='-.', label='bagging_oob_score')# 随机森林算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:for n_tree in pbar:rf = RandomForest(n_trees=n_tree, max_features='sqrt')rf.fit(X, y)train_score.append(rf.score(X, y))oob_score.append(rf.oob_score)pbar.set_postfix({'n_tree': n_tree, 'train_score': train_score[-1], 'oob_score': oob_score[-1]})
plt.plot(num_trees, train_score, color='red', linestyle='--', label='random_forest_train_score')
plt.plot(num_trees, oob_score, color='red', linestyle=':', label='random_forest_oob_score')plt.ylabel('Score')
plt.xlabel('Number of trees')
plt.legend()
plt.show()
提升算法
提升算法是另一种集成学习的框架,思路是利用当前模型的偏差来调整训练数据的权重

适应提升


from sklearn.ensemble import AdaBoostClassifier
# 初始化stump
stump = DTC(max_depth=1, min_samples_leaf=1, random_state=0)# 弱分类器个数
M = np.arange(1, 101, 5)
bg_score = []
rf_score = []
dsc_ada_score = []
real_ada_score = []
plt.figure()with tqdm(M) as pbar:for m in pbar:# bagging算法bc = BaggingClassifier(estimator=stump, n_estimators=m, random_state=0)bc.fit(X_train, y_train)bg_score.append(bc.score(X_test, y_test))# 随机森林算法rfc = RandomForestClassifier(n_estimators=m, max_depth=1, min_samples_leaf=1, random_state=0)rfc.fit(X_train, y_train)rf_score.append(rfc.score(X_test, y_test))# 离散 AdaBoost,SAMME是分步加性模型(stepwise additive model)的缩写dsc_adaboost = AdaBoostClassifier(estimator=stump, n_estimators=m, algorithm='SAMME', random_state=0)dsc_adaboost.fit(X_train, y_train)dsc_ada_score.append(dsc_adaboost.score(X_test, y_test))# 实 AdaBoost,SAMME.R表示弱分类器输出实数real_adaboost = AdaBoostClassifier(estimator=stump, n_estimators=m, algorithm='SAMME.R', random_state=0)real_adaboost.fit(X_train, y_train)real_ada_score.append(real_adaboost.score(X_test, y_test))# 绘图
plt.plot(M, bg_score, color='blue', label='Bagging')
plt.plot(M, rf_score, color='red', ls='--', label='Random Forest')
plt.plot(M, dsc_ada_score, color='green', ls='-.', label='Discrete AdaBoost')
plt.plot(M, real_ada_score, color='purple', ls=':', label='Real AdaBoost')
plt.xlabel('Number of trees')
plt.ylabel('Test score')
plt.legend()
plt.tight_layout()
plt.savefig('output_26_1.png')
plt.savefig('output_26_1.pdf')
plt.show()
#%%
GBDT算法
GBDT算法中应用广泛的是XGBoost,其在损失函数中添加与决策树复杂度相关的正则化约束,防止单个弱学习发生过拟合现象。
# 安装并导入xgboost库
!pip install xgboost
import xgboost as xgb
from sklearn.datasets import make_friedman1
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor, RandomForestRegressor, \StackingRegressor, AdaBoostRegressor# 生成回归数据集
reg_X, reg_y = make_friedman1(n_samples=2000, # 样本数目n_features=100, # 特征数目noise=0.5, # 噪声的标准差random_state=0 # 随机种子
)# 划分训练集与测试集
reg_X_train, reg_X_test, reg_y_train, reg_y_test = \train_test_split(reg_X, reg_y, test_size=0.2, random_state=0)
#%%
def rmse(regressor):# 计算regressor在测试集上的RMSEy_pred = regressor.predict(reg_X_test)return np.sqrt(np.mean((y_pred - reg_y_test) ** 2))# XGBoost回归树
xgbr = xgb.XGBRegressor(n_estimators=100, # 弱分类器数目max_depth=1, # 决策树最大深度learning_rate=0.5, # 学习率gamma=0.0, # 对决策树叶结点数目的惩罚系数,当弱分类器为stump时不起作用reg_lambda=0.1, # L2正则化系数subsample=0.5, # 与随机森林类似,表示采样特征的比例objective='reg:squarederror', # MSE损失函数eval_metric='rmse', # 用RMSE作为评价指标random_state=0 # 随机种子
)xgbr.fit(reg_X_train, reg_y_train)
print(f'XGBoost:{rmse(xgbr):.3f}')# KNN回归
knnr = KNeighborsRegressor(n_neighbors=5).fit(reg_X_train, reg_y_train)
print(f'KNN:{rmse(knnr):.3f}')# 线性回归
lnr = LinearRegression().fit(reg_X_train, reg_y_train)
print(f'线性回归:{rmse(lnr):.3f}')# bagging
stump_reg = DecisionTreeRegressor(max_depth=1, min_samples_leaf=1, random_state=0)
bcr = BaggingRegressor(estimator=stump_reg, n_estimators=100, random_state=0)
bcr.fit(reg_X_train, reg_y_train)
print(f'Bagging:{rmse(bcr):.3f}')# 随机森林
rfr = RandomForestRegressor(n_estimators=100, max_depth=1, max_features='sqrt', random_state=0)
rfr.fit(reg_X_train, reg_y_train)
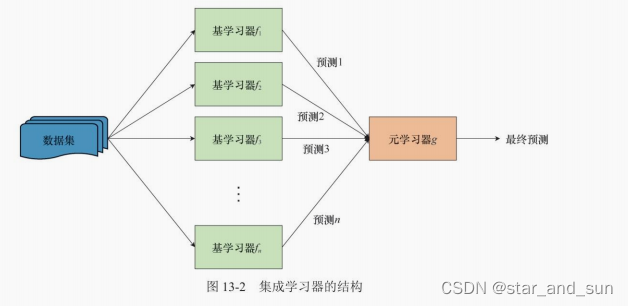
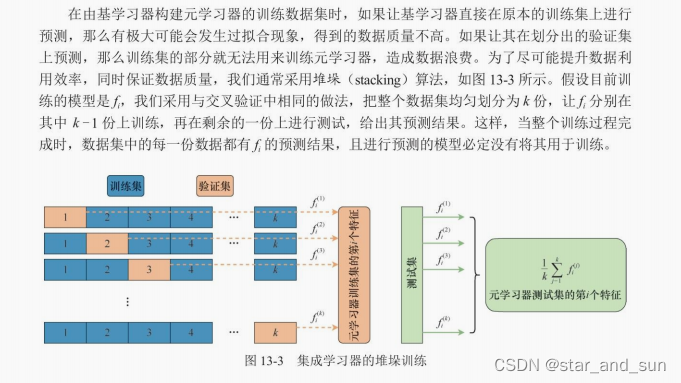
print(f'随机森林:{rmse(rfr):.3f}')# 堆垛,默认元学习器为带L2正则化约束的线性回归
stkr = StackingRegressor(estimators=[('knn', knnr), ('ln', lnr), ('rf', rfr)
])
stkr.fit(reg_X_train, reg_y_train)
print(f'Stacking:{rmse(stkr):.3f}')# 带有输入特征的堆垛
stkr_pt = StackingRegressor(estimators=[('knn', knnr), ('ln', lnr), ('rf', rfr)
], passthrough=True)
stkr_pt.fit(reg_X_train, reg_y_train)
print(f'带输入特征的Stacking:{rmse(stkr_pt):.3f}')# AdaBoost,回归型AdaBoost只有连续型,没有离散型
abr = AdaBoostRegressor(estimator=stump_reg, n_estimators=100, learning_rate=1.5, loss='square', random_state=0)
abr.fit(reg_X_train, reg_y_train)相关文章:

机器学习——集成学习和梯度提升决策树
集成学习 不同的算法都可以对解决同一个问题,但是可能准确率不同,集成学习就是不同算法按照某种组合来解决问题,使得准确率提升。 那怎么组合算法呢? 自举聚合算法**(bagging)** 顾名思义是 自举聚合 自举…...
MYSQL 查看SQL执行计划
一、explain explain select id,db,user,host,command,time,state,info from information_schema.processlist order by time desc; id: 查询的标记,可以查看不同查询的执行顺序。 select_type: 查询的类型,如SIMPLE、SUBQUERY、PRIMARY等。 table: …...
系统架构之系统安全能力的MPAM)
ARM-V9 RME(Realm Management Extension)系统架构之系统安全能力的MPAM
安全之安全(security)博客目录导读 关于RME的MPAM变化的完整定义见在《Arm Architecture Reference Manual Supplement, Memory System Resource Partitioning and Monitoring (MPAM), for A-profile architecture》中详细说明。 实现RME的处理元件(PE)能够生成一个2位的MPAM_…...

cuda 架构设置
import torch torch.cuda.get_device_capability(0) 添加cmake options: -DCMAKE_CUDA_ARCHITECTURES86 -DCMAKE_CUDA_COMPILER/usr/local/cuda-11.8/bin/nvcc cmake工程出现“CMAKE_CUDA_ARCHITECTURES must be non-empty if set.“的解决方法_failed to detec…...

基于 Vue 3 封装一个 ECharts 图表组件
在前端开发中,数据可视化是展示数据的重要方式之一。ECharts 是一个强大的开源可视化库,能够帮助我们轻松地创建各种图表。本文将介绍如何在 Vue 3 项目中使用 ECharts 封装一个图表组件。 代码 <template><div ref"chartRef" styl…...
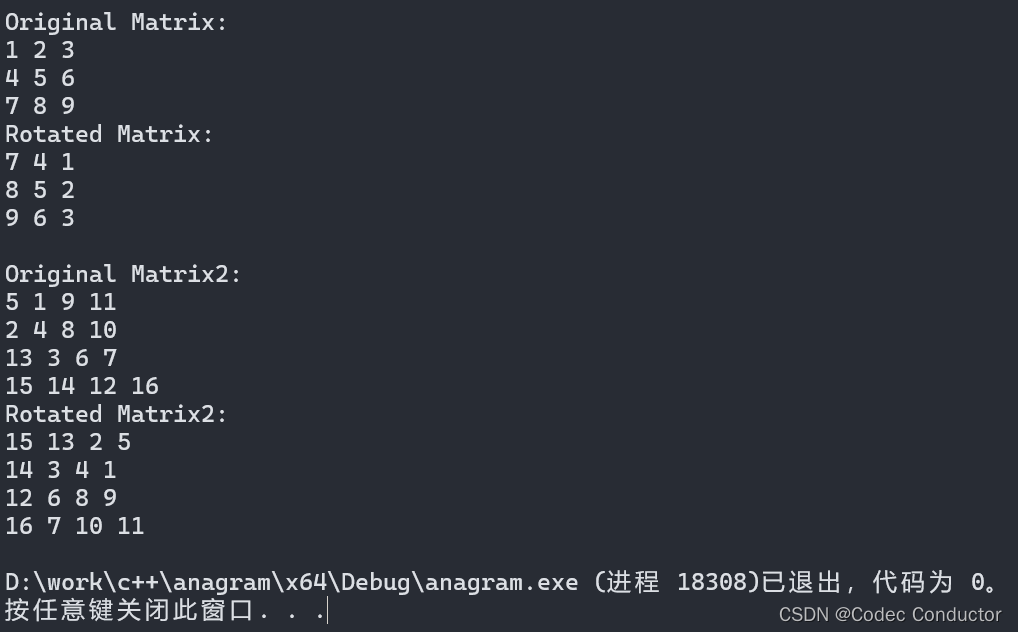
LeetCode 算法: 旋转图像c++
原题链接🔗: 旋转图像 难度:中等⭐️⭐️ 题目 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图…...

Java Android 静态内部类 以及优雅实现单例模式/避免handler内存泄漏
前言 Java 中的静态内部类(Static Nested Class)是定义在另一个类里面的一个静态类。它和普通的内部类有些区别,主要是静态内部类不需要依赖于外部类的实例就可以被创建和访问。这种类的特性使得它非常适合用来作为辅助类,用于支持外部类的功能。 特点以及使用场景 静态内…...

Flink协调器Coordinator及自定义Operator
Flink协调器Coordinator及自定义Operator 最近的项目开发过程中,使用到了Flink中的协调器以及自定义算子相关的内容,本篇文章主要介绍Flink中的协调器是什么,如何用,以及协调器与算子间的交互。 协调器Coordinator Flink中的协调…...

C调用C++中的类
文章目录 测试代码 测试代码 在C语言中调用C类,需要遵循几个步骤: 在C代码中,确保C类的函数是extern “C”,这样可以防止名称修饰(name mangling)。 使用头文件声明C类的公共接口,并且为这个…...
NFTScan 正式上线 Sei NFTScan 浏览器和 NFT API 数据服务
2024 年 6 月 12 号,NFTScan 团队正式对外发布了 Sei NFTScan 浏览器,将为 Sei 生态的 NFT 开发者和用户提供简洁高效的 NFT 数据搜索查询服务。NFTScan 作为全球领先的 NFT 数据基础设施服务商,Sei 是继 Bitcoin、Ethereum、BNBChain、Polyg…...

2024年高考:计算机相关专业前景分析与选择建议
2024年高考结束,面对计算机专业是否仍具有吸引力的讨论,本文将从行业趋势、就业市场、个人兴趣与能力、专业选择建议等多个角度进行深入分析,以帮助考生和家长做出明智的决策。 文章目录 一、行业趋势与就业市场1. 计算机行业的发展与变革2. …...
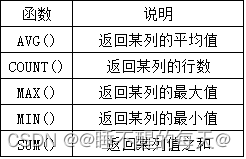
SQL聚合函数---汇总数据
此篇文章内容均来自与mysql必知必会教材,后期有衍生会继续更新、补充知识体系结构 文章目录 SQL聚集函数表:AGV()count()根据需求可以进行组合处理 max()min()max()、min()、avg()组…...

webpack5新特性
webpack5新特性 持久化缓存资源模块moduleIds & chunkIds的优化更智能的tree shakingnodeJs的polyfill脚本被移除支持生成e6/es2015的代码SplitChunk和模块大小Module Federation 持久化缓存 缓存生成的webpack模块和chunk,来改善构建速度cache 会在开发模式被设置成 ty…...

java单体服务自定义锁名称工具类
需求: 操作员能够对自己权限下的用户数据进行数据填充,但是不同操作员之间可能会有重复的用户数据,为了避免操作员覆盖数据或者重复操作数据,应该在操作用户数据时加锁,要求加的这一把锁必须是细粒度的锁,…...
)
整理好了!2024年最常见 20 道并发编程面试题(四)
上一篇地址:整理好了!2024年最常见 20 道并发编程面试题(三)-CSDN博客 七、请解释什么是条件变量(Condition Variable)以及它的用途。 条件变量是一种同步机制,用于在多线程编程中协调线程间的…...

持续交付一
一、 你的项目依赖的 jQuery 版本是 1.0.0 ,Bootstrap 依赖的版本是 1.1.0,而 Chosen 依赖的版本是 1.2.0,看上去都是小版本不一致,一开始并没有发现任何问题,但是如果到后期发现不兼容,可能就为时已晚了。…...

基于 Python 解析 XML 文件并将数据存储到 MongoDB 数据库
1. 问题背景 在软件开发中,我们经常需要处理各种格式的数据。XML 是一种常用的数据交换格式,它可以存储和传输结构化数据。很多网站会提供 XML 格式的数据接口,以便其他系统可以方便地获取数据。 我们有这样一个需求:我们需要从…...

Interview preparation--案例加密后数据的模糊查询
加密数据的模糊查询实现方案 我们知道加密后的数据对模糊查询不是很友好,本篇就针对加密数据模糊查询这个问题来展开讲一讲实现的思路,希望对大家有所启发。为了数据安全我们在开发过程中经常会对重要的数据进行加密存储,常见的有࿱…...

一个简单的R语言数据分析案例
在R语言中,数据分析可以涵盖广泛的领域,包括描述性统计、探索性数据分析、假设检验、数据可视化、机器学习等。以下是一个简单的R语言数据分析案例,该案例将涵盖数据导入、数据清洗、描述性统计、数据可视化以及一个简单的预测模型。 案例&a…...
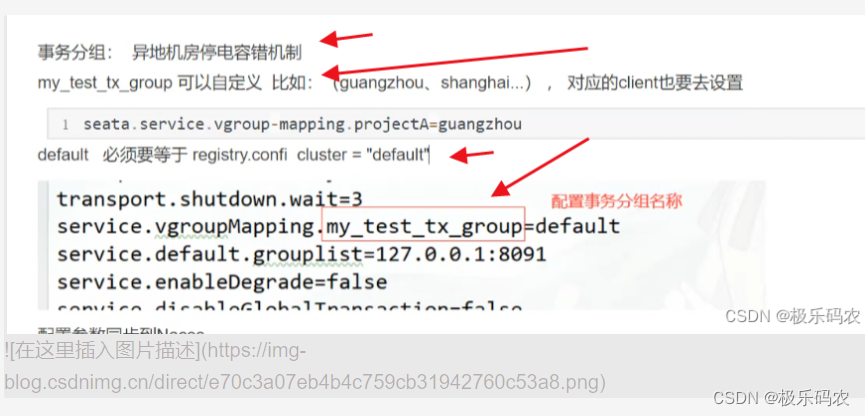
springCloudAlibaba之分布式事务组件---seata
Seata Sea学习分布式事务Seata二阶段提交协议AT模式TCC模式 Seata服务搭建Seata Server(事务协调者TC)环境搭建seata服务搭建-db数据源seata服务搭建-nacos启动seata服务 分布式事务代码搭建-client端搭建接入微服务应用 Sea学习 事务:事务是…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
