【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】线性分类模型损失函数对比
本节均以二分类问题为例进行展开,统一定义类别标签 y ∈ { + 1 , − 1 } y\in\{+1,-1\} y∈{+1,−1},则分类正确时 y f ( x ; w ) > 0 yf(x;w)>0 yf(x;w)>0,且值越大越正确;错误时 y f ( x ; w ) < 0 yf(x;w)<0 yf(x;w)<0,且值越小越错误。不同损失函数间的损失随 y f ( x ; w ) yf(x;w) yf(x;w)变化如下图所示:
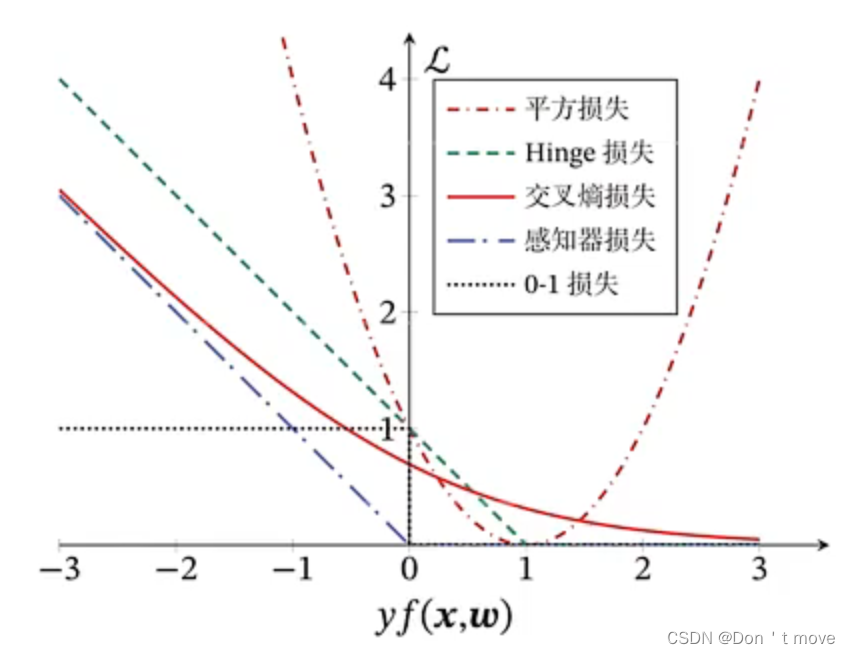
平方损失
L = ( y − f ( x ; w ) ) 2 = y 2 − 2 y f ( x ; w ) + f 2 ( x ; w ) = 1 − 2 y f ( x ; w ) + y 2 f 2 ( x ; w ) = ( 1 − y f ( x ; w ) ) 2 \begin{aligned} \mathcal{L} &=(y-f(x;w))^2 \\ &=y^2-2yf(x;w)+f^2(x;w) \\ &=1-2yf(x;w)+y^2f^2(x;w) \\ &=(1-yf(x;w))^2 \end{aligned} L=(y−f(x;w))2=y2−2yf(x;w)+f2(x;w)=1−2yf(x;w)+y2f2(x;w)=(1−yf(x;w))2
对于平方损失来说,当 y f ( x ; w ) < 1 yf(x;w)<1 yf(x;w)<1时,损失函数单调递减,此时如果用梯度下降进行优化,最终会收敛于点1。但当 y f ( x ; w ) > 1 yf(x;w)>1 yf(x;w)>1时,损失函数单调递减,同样在进行优化时还是会收敛于1,但事实上 y f ( x ; w ) yf(x;w) yf(x;w)越大说明分类越正确。因此可以说,平方损失不适合做分类任务。
Logistic回归的损失函数(交叉熵损失)
L = − I ( y = 1 ) log σ ( f ( x ; w ) ) − I ( y = − 1 ) log ( 1 − σ ( f ( x ; w ) ) ) = − I ( y = 1 ) log σ ( f ( x ; w ) ) − I ( y = − 1 ) log ( σ ( − f ( x ; w ) ) ) = − log σ ( y f ( x ; w ) ) = log σ − 1 ( y f ( x ; w ) ) = log ( 1 + exp ( − y f ( x ; w ) ) ) \begin{aligned} \mathcal{L} &=-I(y=1)\log\sigma(f(x;w))-I(y=-1)\log(1-\sigma(f(x;w)))\\ &=-I(y=1)\log\sigma(f(x;w))-I(y=-1)\log(\sigma(-f(x;w)))\\ &=-\log\sigma(yf(x;w))\\ &=\log\sigma^{-1}(yf(x;w))\\ &=\log(1+\exp(-yf(x;w))) \end{aligned} L=−I(y=1)logσ(f(x;w))−I(y=−1)log(1−σ(f(x;w)))=−I(y=1)logσ(f(x;w))−I(y=−1)log(σ(−f(x;w)))=−logσ(yf(x;w))=logσ−1(yf(x;w))=log(1+exp(−yf(x;w)))
对于函数 σ ( x ) \sigma(x) σ(x),可证 1 − σ ( x ) = σ ( − x ) 1-\sigma(x)=\sigma(-x) 1−σ(x)=σ(−x),且 I I I是指示函数,
I ( y = 1 ) = 1 y = 1 = { 1 y = 1 0 y = − 1 I(y=1)=\mathbb{1}_{y=1}=\left\{\begin{aligned} &1&y=1\\\\ &0&y=-1 \end{aligned}\right. I(y=1)=1y=1=⎩ ⎨ ⎧10y=1y=−1
I ( y = − 1 ) = 1 y = − 1 = { 1 y = − 1 0 y = 1 I(y=-1)=\mathbb{1}_{y=-1}=\left\{\begin{aligned} &1&y=-1\\\\ &0&y=1 \end{aligned}\right. I(y=−1)=1y=−1=⎩ ⎨ ⎧10y=−1y=1
由图像可知,随着 y f ( x ; w ) yf(x;w) yf(x;w)的增大,函数损失逐渐减小最终趋于0。这样虽然满足了 y f ( x ; w ) yf(x;w) yf(x;w)越大分类效果越好的条件,但其实这是没必要的,因为当损失大于0时就可以完成分类任务。因此虽然说交叉熵损失可以满足分类要求,但造成了一些不必要的计算,仍然具有改进空间。
感知器的损失函数
L = max ( 0 , − y f ( x ; w ) ) \mathcal{L}=\max(0,-yf(x;w)) L=max(0,−yf(x;w))
感知器损失解决了交叉熵损失的问题。感知器损失是专门为分类而设计的损失函数,其结果与真实效果基本一致。
软间隔支持向量机的损失函数(Hinge损失)
L = max ( 0 , 1 − y f ( x ; w ) ) \mathcal{L}=\max(0,1-yf(x;w)) L=max(0,1−yf(x;w))
Hinge损失与感知器损失在几何上的不同仅仅在于Hinge损失在感知器损失的基础上向右平移了一个单位,这就导致了Hinge损失对距离分界面较近的样本( y f ( x ; w ) yf(x;w) yf(x;w)落在0到1之间)造成一定的惩罚。
结论
从模型健壮性角度来讲,选择支持向量机(Hinge损失)来解决一般分类问题的效果更好
各线性分类模型对比如下表所示

XOR问题
感知器和支持向量机虽然在线性可分问题上表现良好,但其无法解决非线性可分问题,例如XOR(异或)问题。
假设空间中有两个变量 ( x 1 , x 2 ) (x_1,x_2) (x1,x2),对两个变量分别取与、或、异或逻辑运算,结果如下图所示。

对于与运算和或运算产生的结果来说,总能找到一个分界面来把两类分开,也就是说这两个结果产生的数据集是线性可分的;但异或运算的结果无法直接找到一个分界面,也就是说它的结果数据是非线性可分的。XOR这类非线性可分问题是无法通过线性分类器来解决的。
要解决这类问题,可以借助使用”基函数“的广义线性模型,也就是把线性模型过一个基函数,让线性模型变为非线性的,也就是将 f ( x ) = w T x f(x)=w^Tx f(x)=wTx变成 f ( ϕ ( x ) ) = w T ϕ ( x ) f(\phi(x))=w^T\phi(x) f(ϕ(x))=wTϕ(x),这样就实现了将非线性可分的数据集映射到另一个空间中,映射的数据集在这个空间中是线性可分的。
以下图为例,
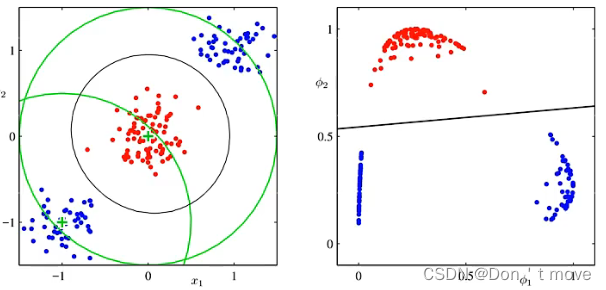
左图表示原来的数据集,可见该数据集是非线性可分的。但它有一个很明显的特征,对于这个数据集来说,可以找到一个中心点,计算样本到中心点的距离,使得中心点某个范围内的为一类,范围外的为另一类,这样就可以构建出一个特征函数,将原本非线性可分的数据集映射到线性可分的数据集上。(上面这个图是按照坐标(-1,-1)附近那个绿色中心点建立的,得到的结果就如右图所示)
相关文章:

【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】线性分类模型损失函数对比
本节均以二分类问题为例进行展开,统一定义类别标签 y ∈ { 1 , − 1 } y\in\{1,-1\} y∈{1,−1},则分类正确时 y f ( x ; w ) > 0 yf(x;w)>0 yf(x;w)>0,且值越大越正确;错误时 y f ( x ; w ) < 0 yf(x;w)<0 yf(x;…...

数组(C语言)(详细过程!!!)
目录 数组的概念 一维数组 sizeof计算数组元素个数 二维数组 C99中的变⻓数组 数组的概念 数组是⼀组相同类型元素的集合。 数组分为⼀维数组和多维数组,多维数组⼀般比较多见的是二维数组。 从这个概念中我们就可以发现2个有价值的信息:(1)数…...

视频生成模型 Dream Machine 开放试用;微软将停止 Copilot GPTs丨 RTE 开发者日报 Vol.224
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE(Real-Time Engagement) 领域内「有话题的 新闻 」、「有态度的 观点 」、「有意思的 数据 」、「有思考的 文…...
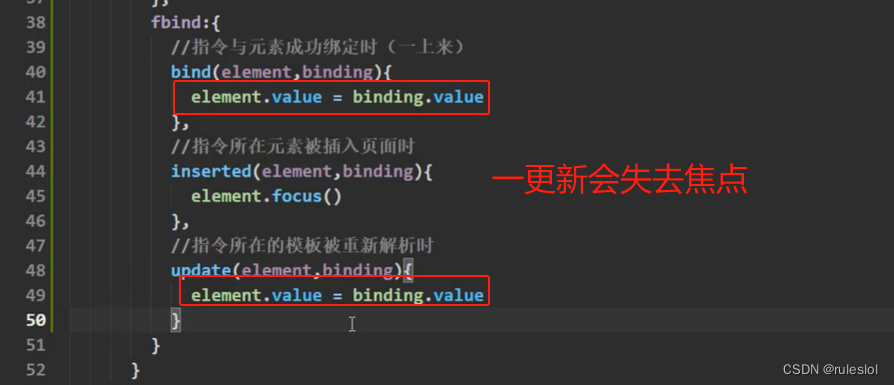
Vue30-自定义指令:对象式
一、需求:创建fbind指定 要用js代码实现自动获取焦点的功能! 二、实现 2-1、步骤一:绑定元素 2-2、步骤二:input元素获取焦点 此时,页面初始化的时候,input元素并没有获取焦点,点击按钮&…...

2024/06/13--代码随想录算法(贪心)3/6|134.加油站、135.分发糖果、860.柠檬水找零、406.根据身高重建队列
134.加油站 力扣链接 class Solution:def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:curSum 0 # 当前累计的剩余油量totalSum 0 # 总剩余油量start 0 # 起始位置for i in range(len(gas)):curSum gas[i] - cost[i]totalSum gas[i] - co…...

机器学习的分类
机器学习分类 机器学习是人工智能的一个分支,它使计算机系统能够从数据中学习并做出决策或预测。机器学习(Machine Learning)是一种基于数据驱动的方法,旨在通过自动化的统计模型和算法从数据中学习和提取模式,以进…...
【Linux】进程控制3——进程程序替换
一,前言 创建子进程的目的之一就是为了代劳父进程执行父进程的部分代码,也就是说本质上来说父子进程都是执行的同一个代码段的数据,在子进程修改数据的时候进行写时拷贝修改数据段的部分数据。 但是还有一个目的——将子进程在运行时指向一个…...
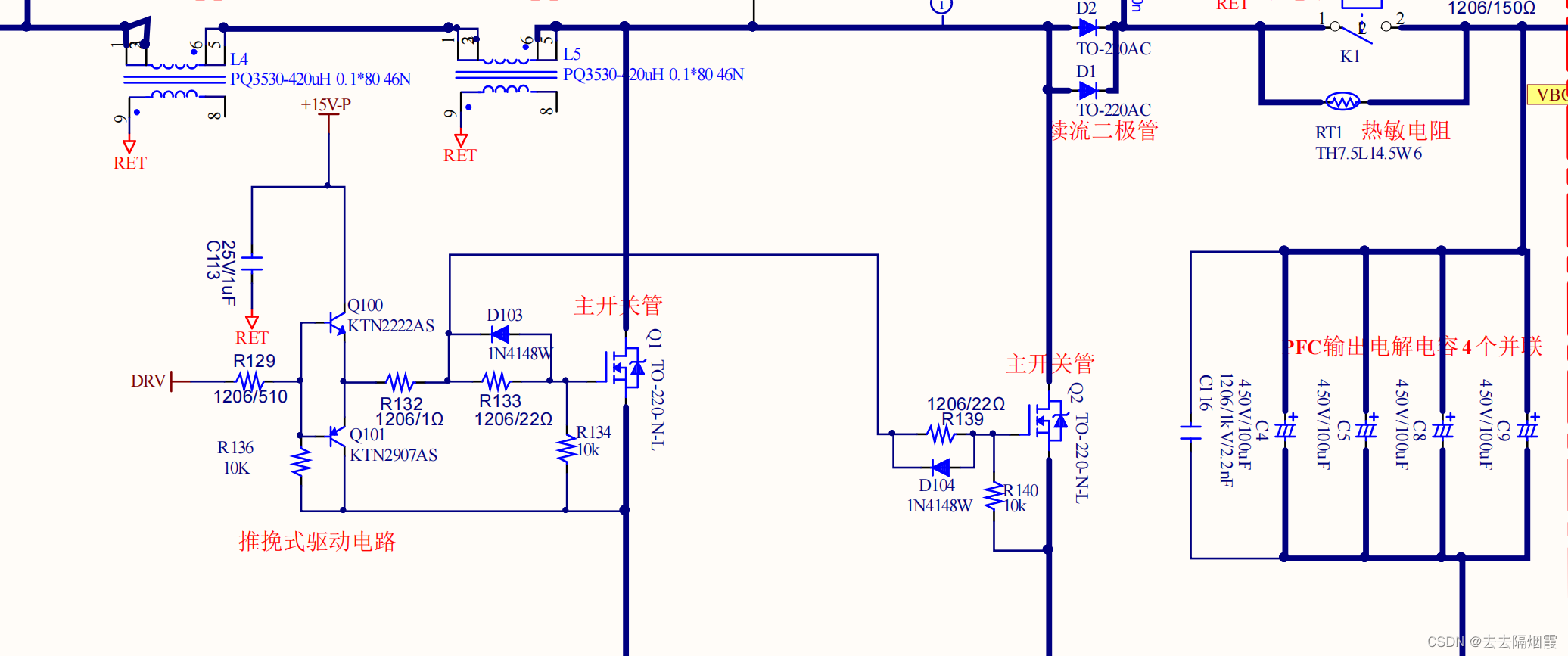
PFC旁路二极管、继电器驱动电路以及PFC主功率
R001和R002以及R003三个电阻作用是限放X电容上的电 整流桥串联两个BJ1和BJ2 电容C3:给整流桥储能,给后续llc供电 PFC工作是正弦波上叠加高频电流 PFC功率部分 2个PFC电感(选择两个磁芯骨架小,有利于散热)、2个续流二极管&…...
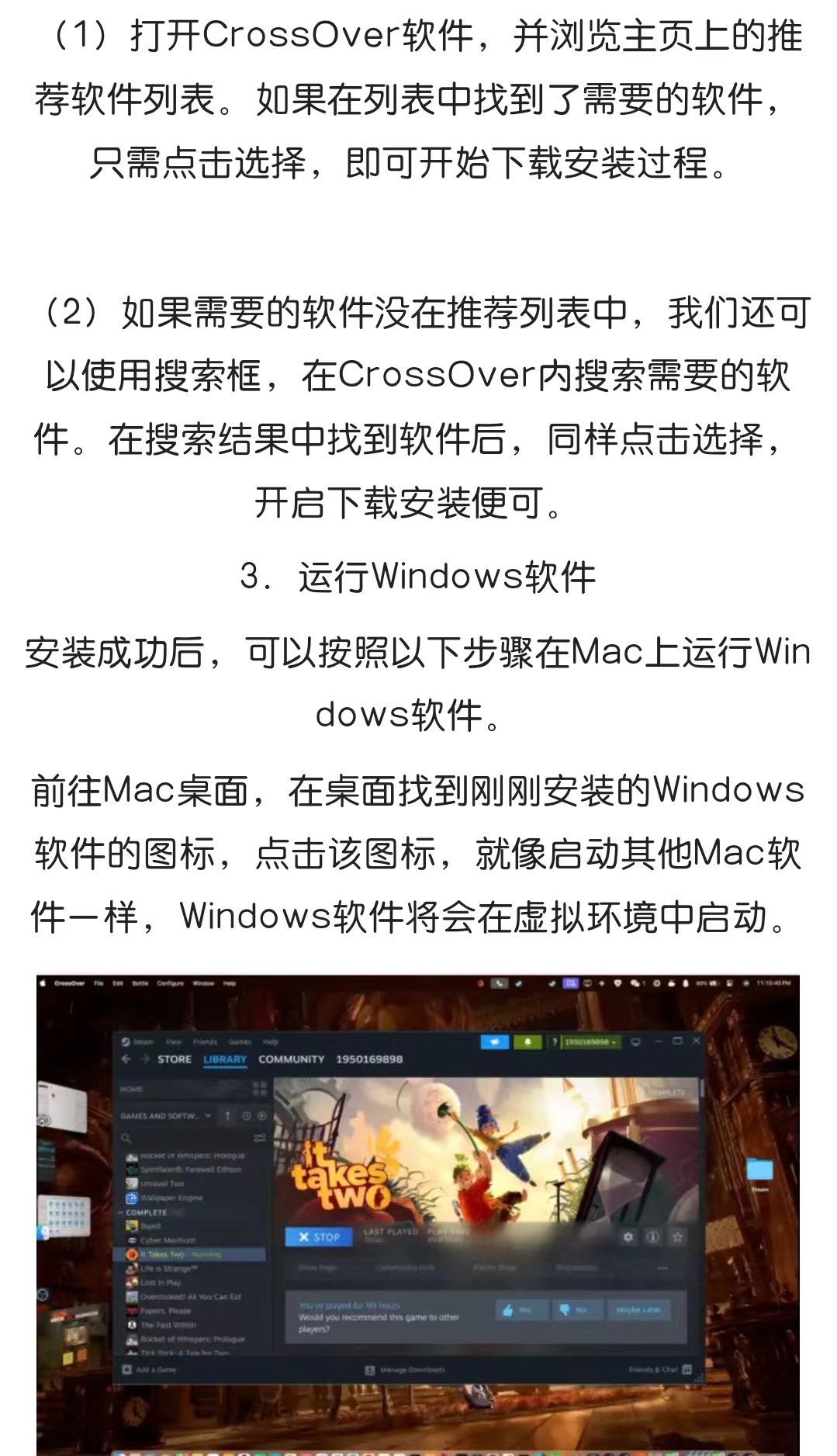
CrossOver 2024软件下载-CrossOver 2024详细安装教程
Crossover软件是一款可以在Mac、Linux和Chromebook上运行Windows程序的软件。 它是一款商业软件,由CodeWeavers公司开发,Crossover不是一个虚拟机或模拟器,它使用Wine技术来将Windows程序直接转换成可以在其他操作系统上运行的程序࿰…...

Spark MLlib机器学习
前言 随着大数据时代的到来,数据处理和分析的需求急剧增加,传统的数据处理工具已经难以满足海量数据的分析需求。Apache Spark作为一种快速、通用的集群计算系统,迅速成为了大数据处理的首选工具。而在Spark中,MLlib(…...
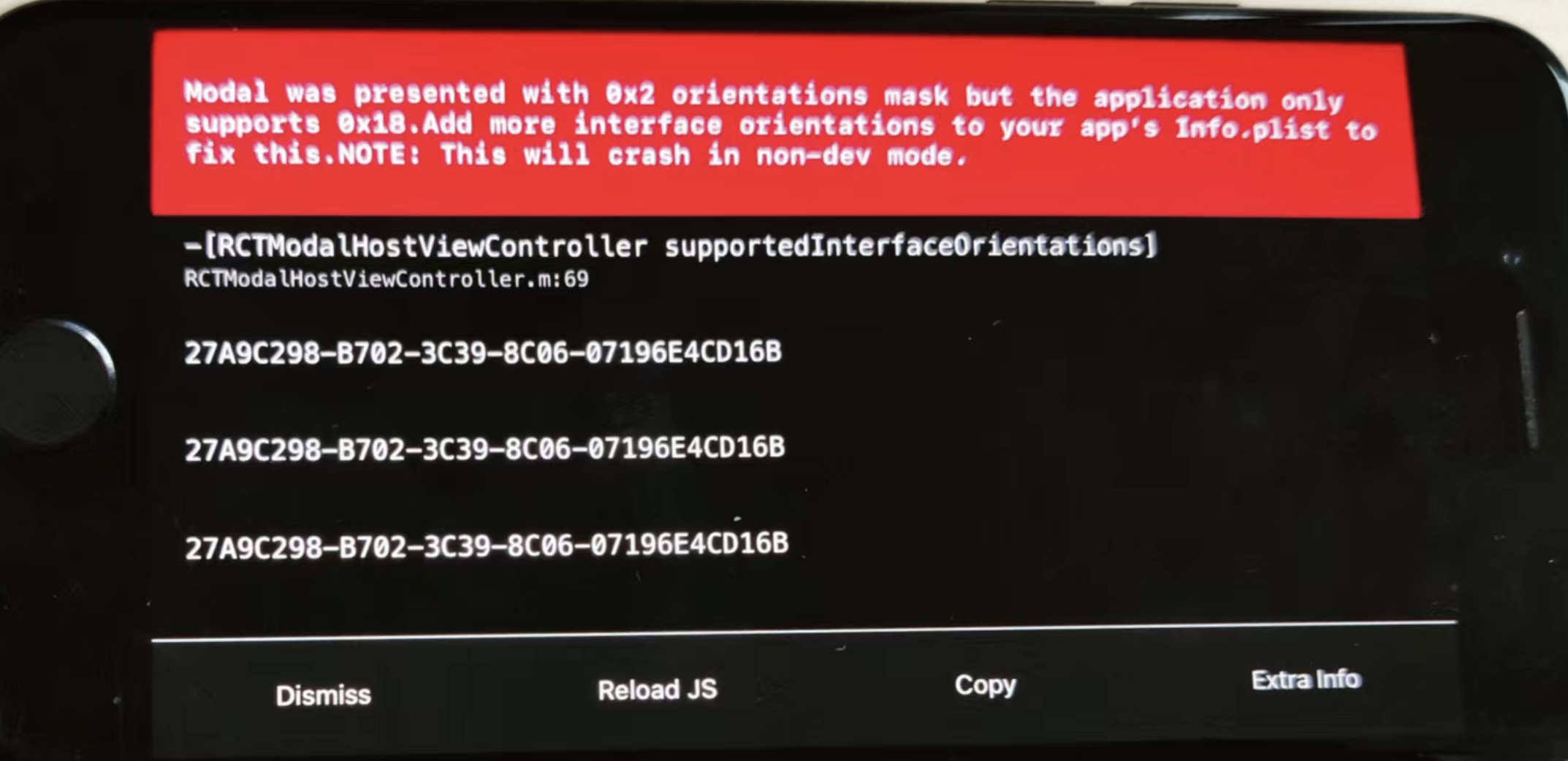
React Native将 ipad 端软件设置为横屏显示后关闭 Modal 弹窗报错
问题: 将 ipad 端软件设置为横屏显示后,关闭 Modal 弹窗报错。 Modal was presented with 0x2 orientations mask but the application only supports 0x18.Add more interface orientations to your apps Info.plist to fix this.NOTE: This will cras…...

JavaEE大作业之班级通讯录系统(前端HTML+后端JavaEE实现)PS:也可选网络留言板、图书借阅系统、寝室管理系统
背景: 题目要求: 题目一:班级通讯录【我们选这个】 实现一个B/S结构的电子通讯录,其中的每条记录至少包含学号、姓名、性别、班级、手机号、QQ号、微信号,需要实现如下功能: (1)…...
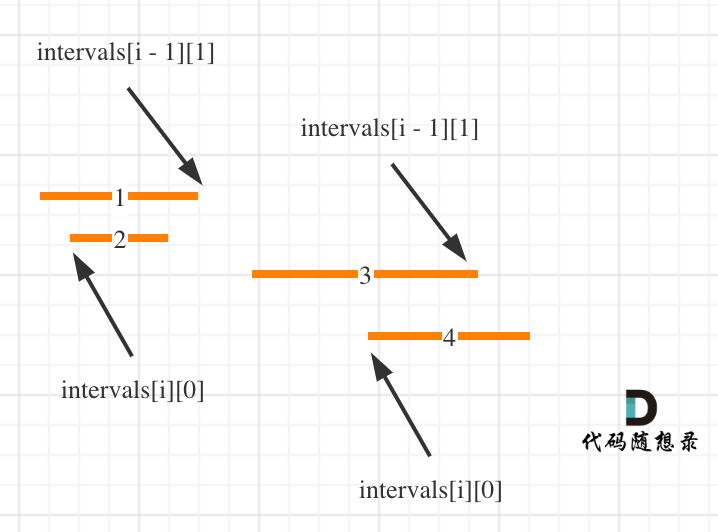
代码随想录算法训练营第37天|● 56.合并区间● 738.单调递增的数字
合并区间 56. 合并区间 - 力扣(LeetCode) 按照左边界从小到大排序之后,如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]的左边界 < intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴…...

SQL Server中的CTE和临时表优化
在SQL Server中,优化查询性能是数据库管理的核心任务之一。使用公用表表达式(CTE)和临时表是两种重要的技术手段。本文将深入探讨CTE如何简化代码,以及临时表如何优化查询性能。通过实例和详尽解释,我们将展示这两种技…...

CCRC信息安全服务资质认证是什么
什么是CCRC认证? CCRC 全称 China Cybersecurity Review Technology and Certification Center。CCRC认证是指中国网络安全审查技术与认证中心进行的信息安全服务资质认证。简称信息安全服务资质认证。 CCRC,即中国网络安全审查技术与认证中心࿰…...
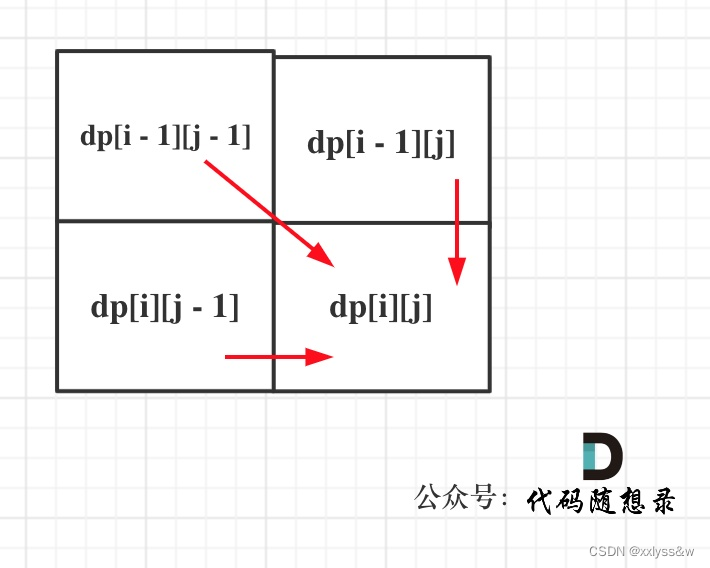
第五十一天 | 1143.最长公共子序列
题目:1143.最长公共子序列718.最长重复子数组的区别是,子序列不要求连续,子数组要求连续。这一差异体现在dp数组含义和递推公式中,本题是子序列,那就要考虑上nums1[i - 1] ! nums2[j - 1]的情况。 本道题与 1.dp数组…...

未来的5-10年,哪些行业可能会被AI代替?
在未来的5-10年,多个行业可能会受到AI技术的影响,其中一些工作可能会被AI所代替。以下是对可能被AI替代的行业及工作的一些概述: 客户服务与代表:随着AI技术的发展,特别是自动话术对话和语音生成技术的进步࿰…...

据报道,FTC 和 DOJ 对微软、OpenAI 和 Nvidia 展开反垄断调查
据《纽约时报》报道,联邦贸易委员会 (FTC) 和司法部 (DOJ) 同意分担调查微软、OpenAI 和 Nvidia 潜在反垄断违规行为的职责。 美国司法部将牵头对英伟达进行调查,而联邦贸易委员会将调查 OpenAI 与其最大投资者微软之间的交易。 喜好儿网 今年 1 月&a…...

人工智能发展历程和工具搭建学习
目录 人工智能的三次浪潮 开发环境介绍 Anaconda Anaconda的下载和安装 下载说明 安装指导 模块介绍 使用Anaconda Navigator Home界面介绍 Environment界面介绍 使用Jupter Notebook 打开Jupter Notebook 配置默认目录 新建文件 两种输入模式 Conda 虚拟环境 添…...

Dijkstra算法的原理
Dijkstra算法的原理可以清晰地分为以下几个步骤和要点: 初始化: 引入一个辅助数组D,其中D[i]表示从起始点(源点)到顶点i的当前已知最短距离。如果起始点与顶点i之间没有直接连接,则D[i]被初始化为无穷大&a…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
