动态规划编译距离
583. 两个字符串的删除操作
方法:dp
状态表示:以i-1和j-1为结尾的字符串world1和world2,抵达相同的字符串所需的最少操作数
属性:最小值
状态计算:world1[i-1]和world2[j-1]相同dp[i][j] = dp[i-1][j-1];
world1[i-1]和world2[j-1]不相同,删去world1:dp[i-1][j] + 1,就变为以i-2和j-1为结尾的字符串world1和world2,抵达相同的字符串所需的最少操作数;同理删除world2:dp[i][j-1] + 1;同时删除world1和world2:dp[i-1][j-1] + 2;
细心的话可以发现dp[i-1][j] + 1 = dp[i-1][j-1] = dp[i][j-1] + 1
所以递推公式dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1)
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size(), m = word2.size();vector<vector<int>> dp(n + 1, vector<int> (m + 1, 0));for (int i = 0; i <= n; ++i) dp[i][0] = i;for (int i = 0; i <= m; ++i) dp[0][i] = i;for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j) {if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];else dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);}return dp[n][m];}
};$时间复杂度O(n*m),空间复杂度O(n*m);
方法2:dp
状态表示:以i-1和j-1为结尾的字符串world1和world2,最大的相同子序列的集合为dp[i][j]
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size(), m = word2.size();vector<vector<int>> dp(n + 1, vector<int> (m + 1, 0));for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j) {if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}return n + m - dp[n][m] * 2;}
};$时间复杂度O(n*m),空间复杂度O(n*m);
72. 编辑距离
方法:dp
简单说一下增加和删除的效果是一样的所以就统一删除了
替换就是在dp[i-1][j-1]的基础上加一个操作
其他的都差不多
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size(), m = word2.size();vector<vector<int>> dp(n + 1, vector<int> (m + 1, 0));for (int i = 0; i <= n; ++i) dp[i][0] = i;for (int i = 0; i <= m; ++i) dp[0][i] = i;for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j) {if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];else dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;}return dp[n][m];}
};$时间复杂度O(n*m),空间复杂度O(n*m);
相关文章:

动态规划编译距离
583. 两个字符串的删除操作方法:dp状态表示:以i-1和j-1为结尾的字符串world1和world2,抵达相同的字符串所需的最少操作数属性:最小值状态计算:world1[i-1]和world2[j-1]相同dp[i][j] dp[i-1][j-1];world1[i-1]和world…...

Netty 教程 – 解码器详解
TCP以流的方式进行数据传输,上层的应用为了对消息进行区分,往往采用如下方式 固定消息长度,累计读取到长度和定长LEN的报文后,就认为读取到了个完整的消息,然后将计数器位置重置在读取下一个报文内容将回车换行符作为…...
Allegro如何自动添加测试点操作指导
Allegro如何自动添加测试点操作指导 在做PCB设计的时候,在一些应用场合下需要给PCB上的网络添加测试点,如下图 测试点除了可以手动逐个添加之外,Allegro还支持自动添加测试点,具体操作如下 点击Manufacture点击Testprep...
【CSS】CSS 背景设置 ③ ( 背景位置-长度值设置 | 背景位置-长度值方位值同时设置 )
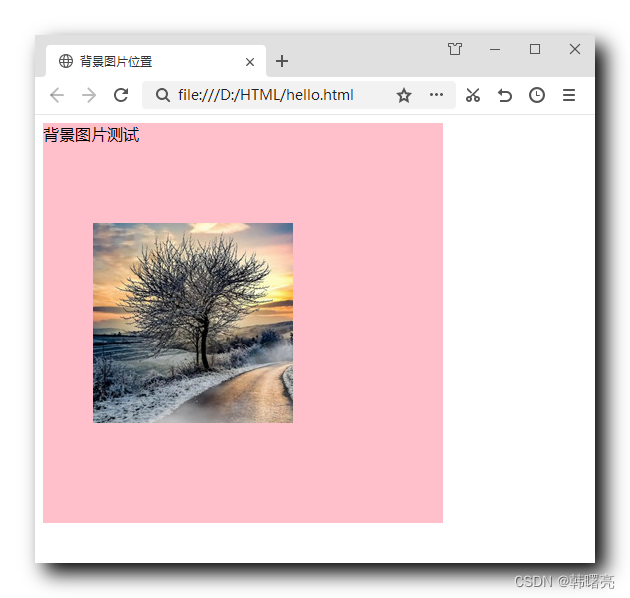
文章目录一、背景位置-长度值设置二、背景位置-长度值方位值同时设置三、完整代码示例一、背景位置-长度值设置 长度值设置 效果展示 : 设置背景位置为具体值 10px 50px : 粉色区域是盒子的区域 , 图片背景位于盒子位置 x 轴方向 10 像素 , y 轴方向 50 像素 ; 在水平方向上 ,…...

AbTest —— 不同场景下的应用模式
文章目录不同人群眼中的 AbTestAbTest 不同的功能倚重用户关联性弱,经典场景为 Feed - 部门组织形式大多非垂直业务用户关联性强,经典场景为 垂类/工具类APP;部门组织形式大多为垂直业务康为定律-组织决定产品形态不同应用模式下服务构建开机…...
fast-api 一款快速将spring的bean发布成接口并生产对应swagger文档调试的轻量级工具
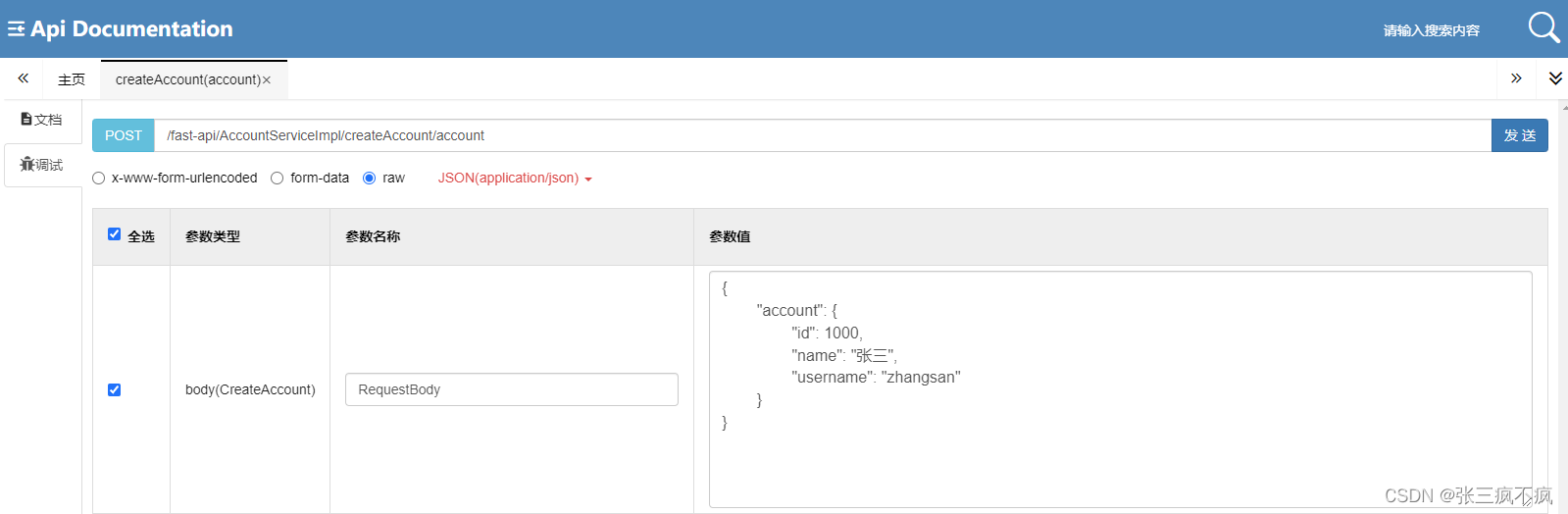
fast-api简介背景开发痛点:分析需求实战fast-api快速上手1. 引入依赖2. FastApiMapping标记service对象3. swagger2/knife4j 在线测试进阶使用开启调试模式支持指定类或包目录发布如何关闭fast-api自定义fast-api的前缀写在最后简介 fast-api 一款快速将spring的bean(service)发…...

以公益之名 让人类发现数学之美
目录 1.品牌理念高举高打 2.创新赛制 赋能品牌 3.全球化的品牌传播 9月26日,2022阿里巴巴全球数学竞赛获奖名单公布,4座金杯分别由平均年龄25岁,来自美国麻省理工学院、美国布朗大学、北京大学在读数学博士斩获。77位获奖者中00后超五成引热…...

JUC并发编程之HashMap(jdk1.7版本)-底层源码探究
目录 JUC并发编程之HashMap(jdk1.7版本)-底层源码探究 HashMap底层源码 - jdk1.7 基本概念 -采取层层递进,问答式 存储Key-Value的结构 常量和成员变量 构造方法 put方法 inflateTable方法 hash方法 indexFor方法 addEntry方法 resize方法 createEntry…...

QT Q_OBJECT 和 signals/slots
Q_OBJECT宏展开 #define Q_OBJECT \ public: \QT_WARNING_PUSH \Q_OBJECT_NO_OVERRIDE_WARNING \static const QMetaObject staticMetaObject; \virtual const QMetaObject *metaObject() const; \virtual void *qt_metacast(const char *); \virtual int qt_metacall(QMetaOb…...
APM新添加UAVCAN设备
简介 UAVCAN是一种轻量级协议,旨在通过CAN总线在航空航天和机器人应用中实现可靠通信。要实现通信,最基本需要data_type_ id, signature、数据结构、设备程序初始化。 添加设备数据结构文件(.uavcan格式) 1.在以下路径添加设备数据结构文件,根据设备类…...

【C++】string类基本用法
文章目录string类基本用法1. 为什么要学习string类?1.1 C语言中的字符串2. 标准库中的string类2.1 string类2.2 string类的常用接口说明小试牛刀1. 仅仅反转字母2. 字符串中第一个唯一字符3. 字符串中最后一个单词的长度string类基本用法 1. 为什么要学习string类&…...

KDZD耐电压高压击穿强度测试仪
一、技术参数 01、输入电压: 交流 220 V。 02、输出电压: 交流 0--50KV ; 直流 0—50kv 。 03、电器容量:3KVA。 04、高压分级:0—50KV,(全程可调)。 05、升压速率:0.1KV/s-…...

数组和指针面试题的补充(细的抠jio)
生命是一条艰险的峡谷,只有勇敢的人才能通过。 ——米歇潘 说明:用的vs都是x86的环境,也就是32位平台。 建议:对于难题来说,一定要配合画图来解决问题。 第一题: #include<stdio.h> int…...
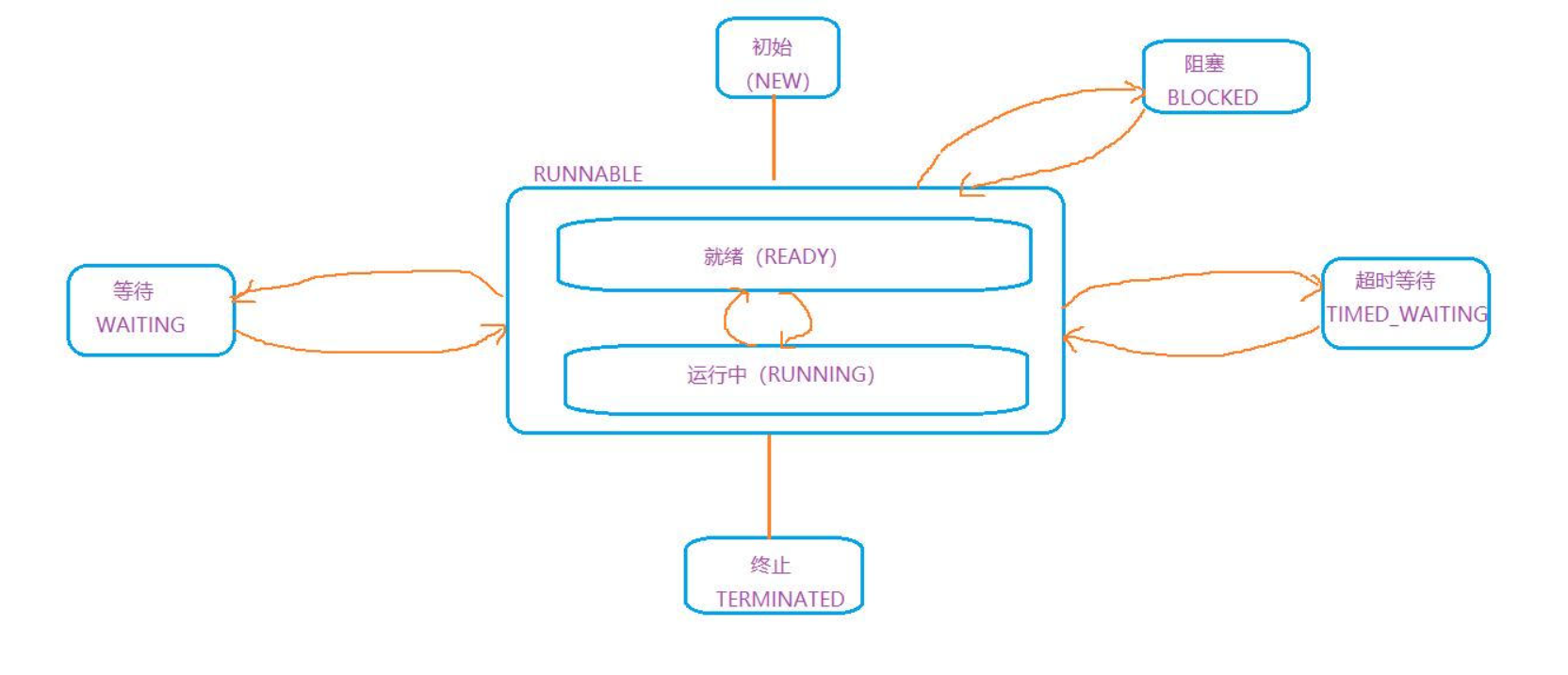
Java多线程基础
文章目录Java多线程基础一、什么是进程与线程?二、线程和进程的区别【重点】三、线程的创建方式【重点】1. 继承Thread类2. 实现Runnable接口3. lambda 表达式四、Thread的常见属性线程中断自己定义一个标志位Thread类提供的静态方法线程的状态Java多线程基础 一、…...
爆品分析第5期 | 一条视频带货3700+,这款斋月不锈钢厨具套装火了!
俗话说民以食为天,吃在任何一种文化中都占据重要的位置,要做出一道美味佳肴,除了食材、烹饪者的自身厨艺之外,还少不了一口好锅。新冠疫情以来,全世界范围内的封闭让很多人养成了居家做饭的习惯,不仅为厨具…...

团队管理的七个要点
要掌握团队管理的要点和做好团队管理工作,不是一件容易的事,但也远非想象中那么难。首先,我个人比较推荐所有团队管理者都能阅读下《经理人参阅:团队管理》(注意该书仅可其官网获得)这本佳作。相信会为你带…...
Go语言容器之map、list和nil
一、map map和C中map一样,里面存放的是key-value键值对在Go中map是引用类型,声明语法:var map变量名 map[key的类型]value的类型package mainimport "fmt"func main() {var mp map[string]intmpls : map[string]int{"one&quo…...

软件测试的案例分析 - 闰年1
(这是关于博客质量分的测试 https://www.csdn.net/qc) 我们谈了不少测试的名词, 软件是人写的, 测试计划和测试用例也是人写的, 人总会犯错误。错误发生之后, 总有人问: 为什么这个bug 没有测出来啊?! 我们看看一类简单的bug是如何发生的,以及如何预防…...
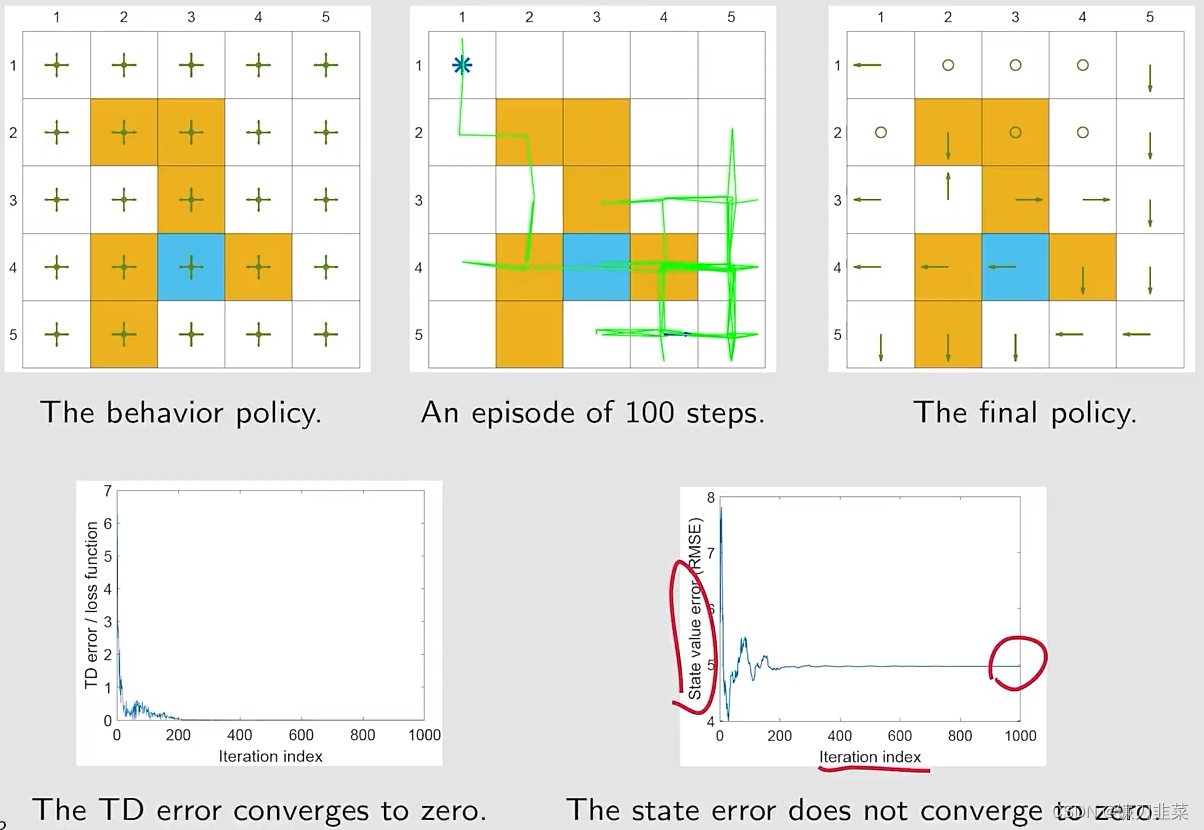
【强化学习】强化学习数学基础:值函数近似
值函数近似Value Function ApproximationMotivating examples: curve fittingAlgorithm for state value estimationObjective functionOptimization algorithmsSelection of function approximatorsIllustrative examplesSummary of the storyTheoretical analysisSarsa with …...
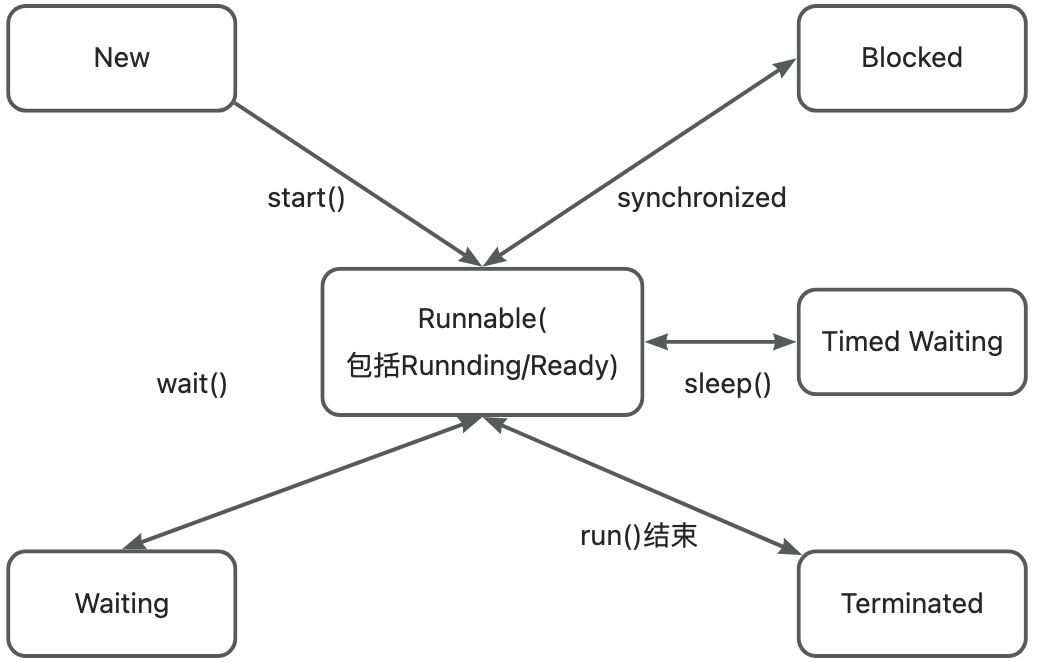
JVM系列——Java与线程,介绍线程原理和操作系统的关系
并发不一定要依赖多线程(如PHP中很常见的多进程并发)。 但是在Java里面谈论并发,基本上都与线程脱不开关系。因此我们讲一下从Java线程在虚拟机中的实现。 线程的实现 线程是比进程更轻量级的调度执行单位。 线程的引入,可以把一个进程的资源分配和执行调…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
