三极管的厄利效应(early effect)
詹姆斯·M·厄利(James M. Early)发现的现象,厄利效应(英语:Early effect),又译厄尔利效应,也称基区宽度调制效应,是指当双极性晶体管(BJT)的集电极-射极电压VCE改变,基极-集电极耗尽宽度WB-C(耗尽区大小)也会跟着改变。此变化称为厄利效应,由詹姆斯·M·厄利(James M. Early)所发现。
现象
图1中的有效中性基区为绿色,基区相邻的耗尽区为画有阴影的淡绿色,中性发射区和集电区为深蓝色,集电区相邻的耗尽区为画有阴影的淡蓝色。从图1中可以看到,若集电极-基极反向偏置增大,则基区相邻的耗尽区越宽,中性基区越窄。

在反向偏置电压的作用下,集电区相邻的耗尽区也会变宽,宽度超过基区相邻的耗尽区,因为集电区掺杂低。中性区和耗尽区的宽度的和要保持不变,因为二者符合电中和原理。集电区变窄不会产生非常大的影响,因为其宽度远大于基区。发射极-基极结不会发生变化,因为电压不变。
基区变窄对于电流的影响有以下两方面:
由于基区变得更窄,电子与空穴复合的可能性更小。若穿过基区的电荷梯度增加,那么注入基区的少子电流会增加。若集电区电压升高,以上因素都会使集电区或晶体管的输出电流增大,如概述图所示的BJT输出特性曲线。特性曲线中电压较大时的切线进行反向外推,其延长线与电压轴相交,在电压轴上截得的负截距称为厄利电压(Early voltage),记为VA。

从厄利效应可以看出,如果BJT的基区宽度发生变化,会导致更大的反向偏置电压在集电极-基极接面,会增加集电极-基极耗尽区宽度,减少基区宽度。总的来说,增加集电极电压(VC),集电极电流(IC)也会跟着上升。
大信号模型
在正向有源区中,厄利效应使集电区电流IC和正向共射极电流放大系数βF发生了改变,通常二者满足下列关系:

其中VCE是集电极-发射极电压VT是热电压kT / qVA是厄利电压(一般为15 V-150 V,对于小型设备会更小)βF0是零偏压时的正向共射极电流放大系数

某些模型把集电极电流校正系数建立在集电极-基极电压VCB(基区宽度调制)而不是集电极-发射极电压VCE的基础上。利用VCB建模在物理上似乎更为合理,因为从厄利效应的物理原因上来看,集电极-基极耗尽层的变宽取决于VCB的变化。计算机模型例如SPICE中所用的模型都使用集电极-基极电压VCB。
小信号模型
在小信号电路模型(如混合π模型)中,厄利效应可以被定义为满足如下关系的电阻:

可看出上式与晶体管的集电极-发射极PN结有关,因此这一电阻定义可解释简单电流镜或有源负载共射极放大器的有限输出电阻。
若与SPICE中保持一致,使用VCB来表示电阻,则上式变为:

对于MOSFET,输出电阻在Shichman-Hodges模型(在非常陈旧的技术中是精确模型)中被定义为:

其中VDS = 漏源极电压,ID = 漏极电流,λ = 沟道长度调制系数,通常与沟道长度L 成反比。由于MOSFET也有类似的双极性,MOSFET中也会使用“厄利效应”这一术语来描述类似的现象。

相关文章:

三极管的厄利效应(early effect)
詹姆斯M厄利(James M. Early)发现的现象,厄利效应(英语:Early effect),又译厄尔利效应,也称基区宽度调制效应,是指当双极性晶体管(BJT)的集电极-射极电压VCE改…...

Maven: 编码GBK的不可映射字符不能编译
使用mvn compile命令,出现错误: 编码GBK的不可映射字符不能编译。这是因为代码或注释中存在中文引起的,一般在ide中会自动处理编译时的字符集,就不会碰到这个错误。这个错误是在生成代码后,其中自动加上了中 文注释,手…...
《web应用技术》第十一次课后作业
1、验证过滤器进行权限验证的原理。 Filter过滤器:javaweb三大组件(Servlet,Filter,Listener)之一;过滤器可以把对资源的请求拦截下来,从而实现一些特殊功能;过滤器一般完成一些通用操作,比如登录校验等。 执行对应的…...

flutter中实现首行缩进两端对齐
刚开始进行搜索,发现很多都是让在每段开始的时候采用空格进行填充,但是采用这种形式之后,不知道为何首行直接溢出了,最后采用下面方法进行实现的。 RichText(text: TextSpan(children: [WidgetSpan(child: Container(width: 20, …...

Vitis HLS 学习笔记--Vitis Accelerated Libraries介绍
目录 1. 简介 2. 库的文件结构 3. 分类介绍 3.1 blas 3.2 codec 3.3 data_analytics 3.4 data_compression 3.5 data_mover 3.6 database 3.7 dsp 3.8 graph 3.9 hpc 3.10 motor_control 3.11 quantitative_finance 3.12 security 3.13 solver 3.14 utils 3…...

Vue3-滑动到最右验证功能
1、思路 1、在登录页面需要启动向右滑块验证 2、效果图 3、文章地址:滑动验证码的实现-vue-simple-verify 2、成分分析 1、由三块构成,分别是底部条、拖动条、拖动移动部分 2、底部条:整体容器,包括背景、边框和文字…...

深入理解MyBatis XML配置文件
MyBatis是一款优秀的持久层框架,简化了数据库操作的复杂性,提高了开发效率。在MyBatis中,XML配置文件扮演了重要角色,用于配置数据源、事务管理、SQL映射等内容。本文将详细介绍MyBatis的XML配置文件,帮助读者更好地理…...

006 CentOS 7.9 elasticsearch7.10.0安装及配置
文章目录 一、安装Elasticsearch 7.10.0二、安装Logstash 7.10.0三、配置防火墙和网络访问可能出现的错误配置 Elasticsearch官方网址: https://www.elastic.co Elasticsearch中文官网地址:https://www.elastic.co/cn/products/elasticsearch https://…...
蚂蚁分类信息系统二开仿么么街货源客模板微商货源网源码(带手机版)
源码介绍 网站采用蚂蚁分类信息系统二次开发,模板仿么么街货源客模板,微商货源网定制版。 模板设计风格简洁,分类信息采用列表形式发布,这种设计方式非常符合度娘 SEO 规则。收录效果是杠杠的。 这个网站风格目前是用来做货源推…...

综合数据分析及可视化实战
【实验目的】 1、掌握数据分析常用的几种扩展库: numpy、pandas、matplotlib。 2、理解数据分析的几种方法,即描述性数据分析,探索性数据分析 和验证性数据分析。 3、理解数据分析的基本步骤:数据准备、数据导入、数据预处理、数 据分析和数据可视化…...

N32G45XVL-STB之移植LVGL(8.4.0)
目录 概述 1 系统软硬件 1.1 软件版本信息 1.2 ST7796-LCD 1.3 MCU IO与LCD PIN对应关系 2 认识LVGL 2.1 LVGL官网 2.2 下载V8.4.0 3 移植LVGL 3.1 硬件驱动实现 3.2 添加LVGL库文件 3.3 移植和硬件相关的代码 3.3.1 驱动接口相关文件介绍 3.3.2 重新接口函数 3…...
SwaggerSpy:一款针对SwaggerHub的自动化OSINT安全工具
关于SwaggerSpy SwaggerSpy是一款针对SwaggerHub的自动化公开资源情报(OSINT)安全工具,该工具专为网络安全研究人员设计,旨在简化广大红队研究人员从SwaggerHub上收集已归档API信息的过程,而这些OSINT信息可以为安全人…...
Python酷库之旅-比翼双飞情侣库(05)
目录 一、xlrd库的由来 二、xlrd库优缺点 1、优点 1-1、支持多种Excel文件格式 1-2、高效性 1-3、开源性 1-4、简单易用 1-5、良好的兼容性 2、缺点 2-1、对.xlsx格式支持有限 2-2、功能相对单一 2-3、更新和维护频率低 2-4、依赖外部资源 三、xlrd库的版本说明 …...

numpy数组transpose方法的基本原理
背景:记录一下numpy数组维度顺序操作 一、具体示例 transpose方法用于交换数组的轴,改变数组的维度顺序。方法的参数是一个代表新轴顺序的元组。 假设你有一个三维数组,其形状是 (a, b, c),即有 a 个块,每个块中有 b…...
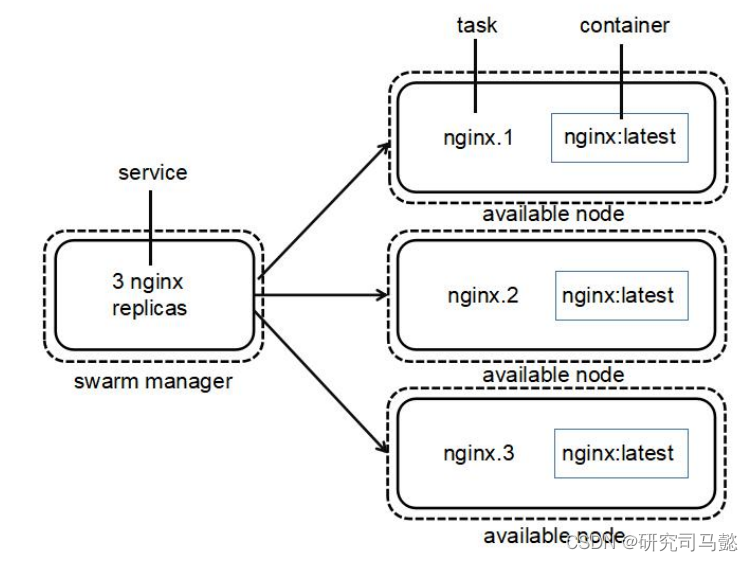
Docker Swarm集群部署管理
Docker Swarm集群管理 文章目录 Docker Swarm集群管理资源列表基础环境一、安装Docker二、部署Docker Swarm集群2.1、创建Docker Swarm集群2.2、添加Worker节点到Swarm集群2.3、查看Swarm集群中Node节点的详细状态信息 三、Docker Swarm管理3.1、案例概述3.2、Docker Swarm中的…...
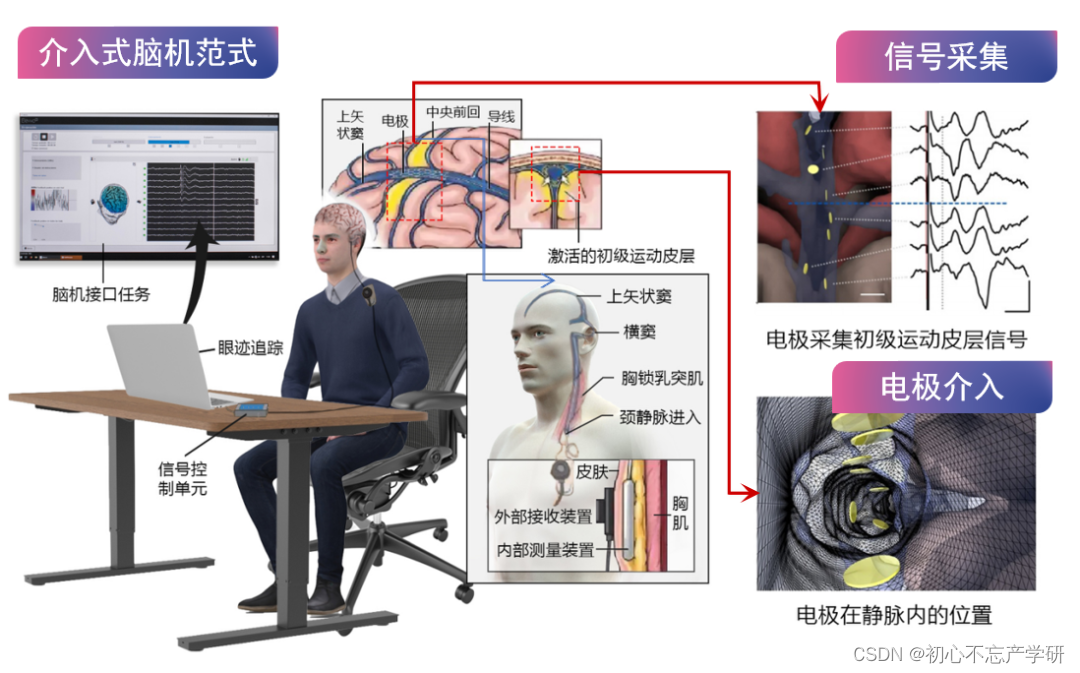
碎片化知识如何被系统性地吸收?
一、方法论 碎片化知识指的是通过各种渠道快速获取的零散信息和知识点,这些信息由于其不完整性和孤立性,不易于记忆和应用。为了系统性地吸收碎片化知识,可以采用以下策略: 1. **构建知识框架**: - 在开始吸收之前&am…...

安鸾学院靶场——安全基础
文章目录 1、Burp抓包2、指纹识别3、压缩包解密4、Nginx整数溢出漏洞5、PHP代码基础6、linux基础命令7、Mysql数据库基础8、目录扫描9、端口扫描10、docker容器基础11、文件类型 1、Burp抓包 抓取http://47.100.220.113:8007/的返回包,可以拿到包含flag的txt文件。…...

ChatGPT:自然语言处理的新纪元与OpenAI的深度融合
随着人工智能技术的蓬勃发展,自然语言处理(NLP)领域取得了显著的进步。OpenAI作为这一领域的领军者,以其卓越的技术实力和创新能力,不断推动着NLP领域向前发展。其中ChatGPT作为OpenAI的重要成果更是在全球范围内引起了…...

AI引领项目管理新时代:效率与智能并驾齐驱
在数字化浪潮的推动下,项目管理领域正迎来一场由AI技术引领的革新。从自动化任务执行到智能决策支持,AI技术的应用正让项目管理变得更加高效、精准和智能化。本文将探讨项目管理人员及其实施团队如何运用AI技术,以及这些技术如何助力项目管理…...
)
AUTOSAR汽车电子嵌入式编程精讲300篇-电池管理系统中 CAN 通信模块的设计与应用(中)
目录 2.3 BMS 中 CAN 通信模块软硬件设计 2.3.1 CAN 通信模块硬件电路设计 2.3.2 CAN 通信模块软件设计 2.3.2.1 CAN 底层程序设计 2.3.2.2 CAN 底层初始化 2.3.2.3 CAN 底层接收 3.3.1.3 CAN 底层发送 2.4 通信协议的实现 2.4.1 整车通信协议的实现 2.4.2 充电机通信协议的实现…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
