当前位置： 首页 > news >正文

idea 新建一个 JSP（JavaServer Pages）项目

news 2026/2/8 14:28:29

  1. 环境设置：

    • 确保你的开发环境中已经安装了 Java 开发工具包（JDK）和一个 Java Web 开发的集成开发环境（IDE），比如 Eclipse、IntelliJ IDEA 或者 NetBeans。
    • 你还需要一个 Web 服务器，比如 Apache Tomcat。

  2. 创建项目：

    • 在你选择的 IDE 中创建一个新的 Java Web 项目。
    • 选择 JSP 作为你的 Web 技术。

  3. 项目结构：

    • 通常，JSP 项目会有一个 Web 内容目录（Web Content），其中包含 JSP 文件、HTML 文件、CSS 文件、JavaScript 文件等。通常情况下，JSP 文件会放在名为 “WEB-INF” 的目录下，以保护它们不被直接访问。
    • 创建一个 JSP 文件来开始你的项目。可以先编写一些简单的代码，比如输出 “Hello World”，以确保一切都设置正确。

  4. Servlets 和 JavaBean（可选）：

    • 在复杂的 JSP 项目中，你可能需要使用 Servlets 处理业务逻辑，以及 JavaBean 来管理数据。
    • Servlets 是 Java 类，可以接收来自客户端的请求并生成响应。你可以在 Servlet 中处理表单提交、数据库操作等。
    • JavaBean 是用于在应用程序中管理数据的 Java 类。在 JSP 中，你可以使用 JavaBean 来存储和检索数据，然后在页面上显示它们。

  5. 前端设计：

    • 设计并开发你的前端界面，可以使用 HTML、CSS、JavaScript 等技术。
    • 在 JSP 文件中嵌入 HTML 和其他前端代码，以呈现动态内容。

  6. 部署和测试：

    • 在你的开发环境中部署项目，并进行测试。确保所有功能都按预期工作。
    • 如果一切顺利，你可以将项目部署到生产环境中，让用户访问你的应用。

  7. 维护和扩展：

    • 定期更新你的项目，添加新功能，修复 bug，并确保它与最新的技术和安全标准保持一致。

相关文章：

idea 新建一个 JSP（JavaServer Pages）项目

环境设置： 确保你的开发环境中已经安装了 Java 开发工具包（JDK）和一个 Java Web 开发的集成开发环境（IDE），比如 Eclipse、IntelliJ IDEA 或者 NetBeans。你还需要一个 Web 服务器，比如 Apache T…...

编程日记 2024/6/14 10:30:33

【名词解释】Unity中的表格布局组件及其使用示例

Unity中的表格布局组件通常指的是GridLayoutGroup，这是一个在Unity的UI系统中用来布局子对象的组件。它可以帮助开发者将UI元素按照网格的形式进行排列，非常适合创建表格、网格视图等布局。 名词解释： GridLayoutGroup：Unity UI…...

编程日记 2024/6/14 10:29:32

判断当前设备为移动端自适应 平板和pc端为375移动端样式

在libs的setRem.js中： let html document.querySelector("html"); function setRem() {let ui_w 375;let cl_w document.documentElement.clientWidth || document.body.clientWidth;cl_w > 750 ? cl_w 375 : "";html.style.fontSize …...

编程日记 2024/6/14 10:28:31

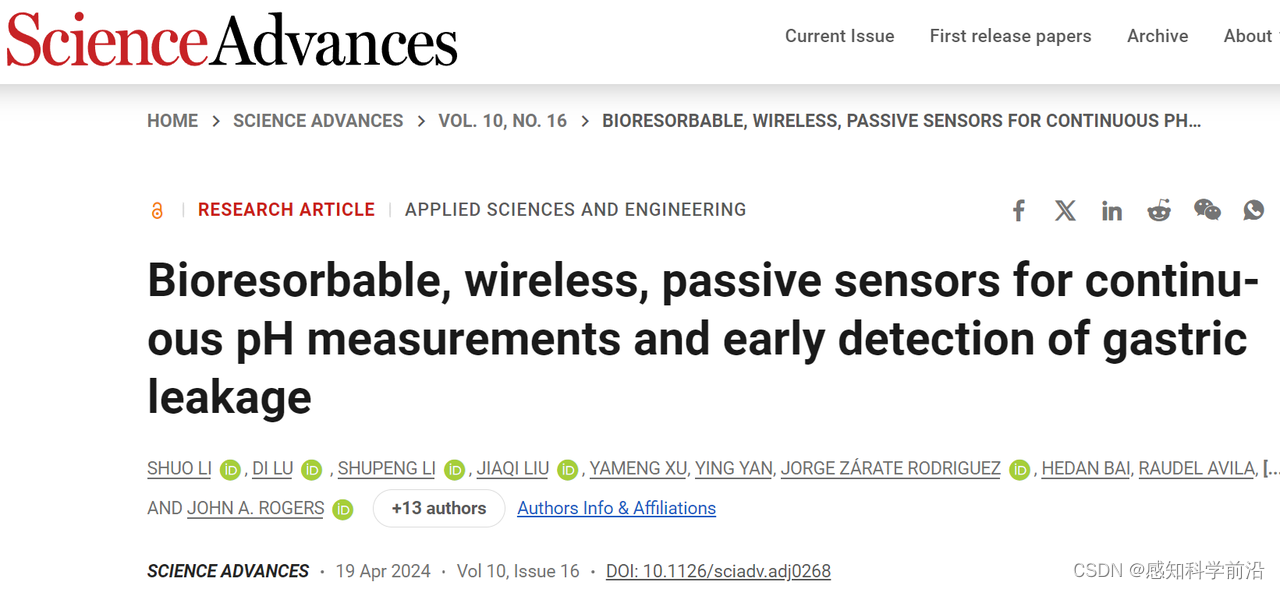
Science Advances|用于胃部pH监测和早期胃漏检测的生物可吸收无线无源柔性传感器（健康监测/柔性传感/柔性电子）

2024年4月19日，美国西北大学 John A. Rogers和中国科学技术大学吕頔(Di Lu)团队，在《Science Advances》上发布了一篇题为“Bioresorbable, wireless, passive sensors for continuous pH measurements and early detection of gastric leakage”的论文。论文内容如下： 一、…...

编程日记 2024/6/14 10:27:30

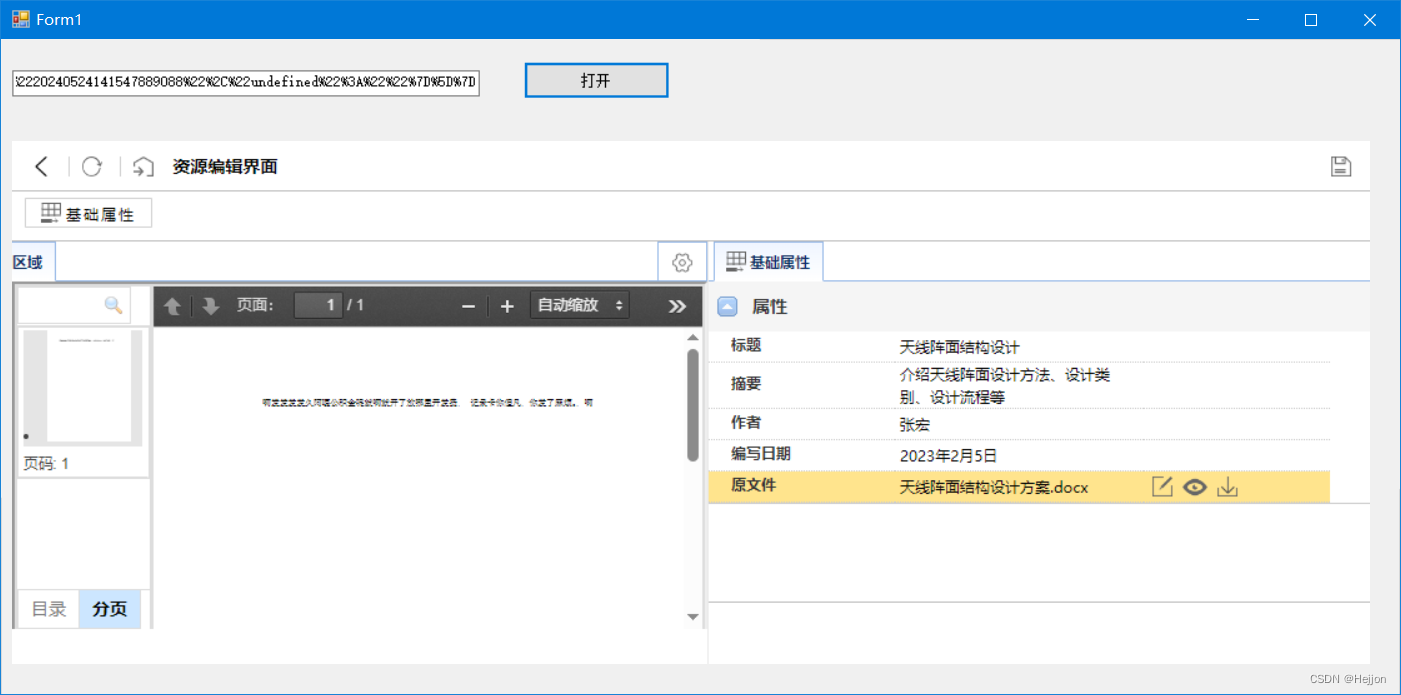
C# 使用 webview2 嵌入网页

需求：C#客户端程序, 窗口里嵌入一个web网页，可通过URL跳转的那种。并且，需要将登录的身份验证信息（token）设置到请求头里。 核心代码如下： // 打开按钮的点击事件 private void openBtn_Click(object sen…...

编程日记 2024/6/14 10:24:26

公司面试题总结（五）

25.谈一谈箭头函数与普通函数的区别，箭头函数主要解决什么问题？ 箭头函数与普通函数的区别： ⚫ 语法简洁性： ◼ 箭头函数使用>符号定义，省略了 function 关键字，使得语法更为紧凑。 ◼ 对于单行函…...

编程日记 2024/6/14 10:23:25

Flutter笔记：关于WebView插件的用法（上）

Flutter笔记 关于WebView插件的用法（上） - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite：http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:htt…...

编程日记 2024/6/14 10:21:22

计算机毕业设计Python+Django农产品推荐系统 农产品爬虫 农产品商城 农产品大数据 农产品数据分析可视化 PySpark Hadoop Hive

课题研究的意义，国内外研究现状、水平和发展趋势 研究意义21世纪是一个信息爆炸的时代，人们在日常生活中可接触到的信息量非常之巨大。推荐系统逐步发展，其中又以个性化推荐系统最为瞩目。个性化推荐系统的核心在于个性化推荐算法&#xff0c…...

编程日记 2024/6/14 10:20:20

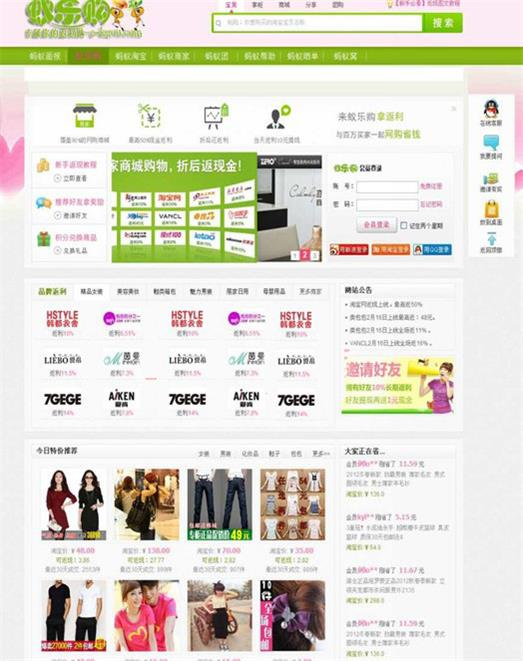
phpcms仿蚁乐购淘宝客网站模板

phpcms仿蚁乐购网站模板，淘宝客行业模板免费下载，该模板网站很容易吸引访客点击，提升ip流量和pv是非常有利的。本套模板采用现在非常流行的全屏自适应布局设计，且栏目列表以简洁，非常时尚大气。页面根据分辨率大小而自…...

编程日记 2024/6/14 10:19:19

leetcode695 岛屿的最大面积

题目 给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。 岛屿的面积是岛上值…...

编程日记 2024/6/14 10:17:16

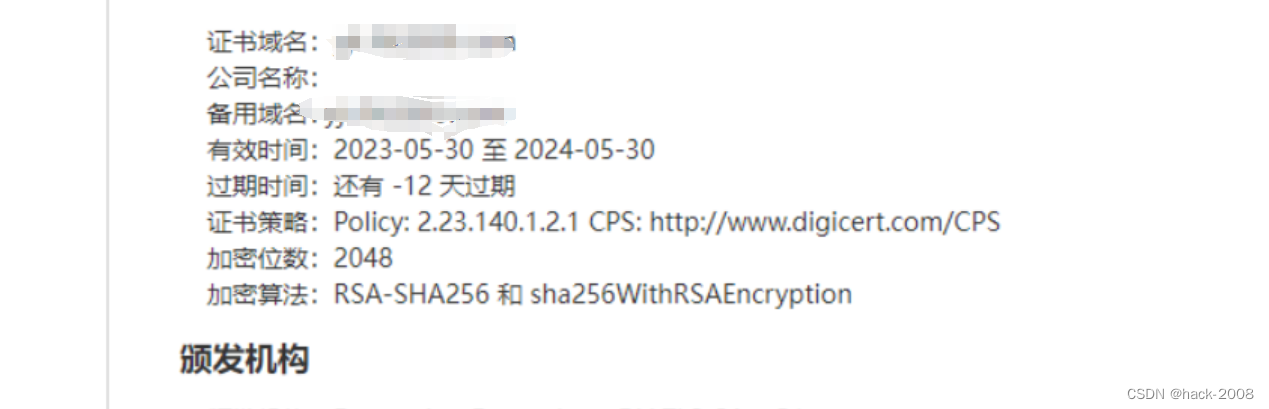
小程序无法调用服务端问题排查

1、问题描述 突然有一天线上的小程序不能登录，经查小程序无法调用。经查无法小程序页面无法调用后台服务。 2、排查过程 由于无法登录小程序发布服务器，无法测试小程序前端服务器到服务端网络，并且小程序无法看到日志。所以就得从服务端和网…...

编程日记 2024/6/14 10:15:14

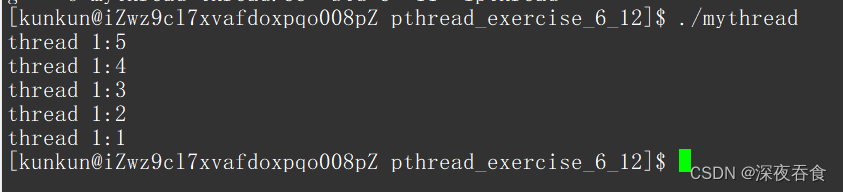
Linux：多线程的操作

多线程操作 进程与线程线程的创建 create_pthread创建线程池给线程传入对象的指针 线程等待 pthread_join退出线程 pthread_exit线程等待参数 retval 与 线程退出参数 retval 线程中断 pthread_cancel获取线程编号 pthread_self线程分离 pthread_detach 进程与线程 进程是资源…...

编程日记 2024/6/14 10:11:08

kunpeng的aarch64架构cpu、openeuler系统、昇腾服务器适配文档转换功能（doc转docx、ppt转pptx）

一、安装flatpak sudo yum install flatpak flatpak remote-add --if-not-exists flathub https://flathub.org/repo/flathub.flatpakrepo二、安装libreoffice flatpak install flathub org.libreoffice.LibreOffice三、使用 对于使用 flatpak 安装的 LibreOffice,不需要手…...

编程日记 2024/6/14 10:10:06

unity 打包PC安装包中常见文件的功能

目录 前言 一、打包好的文件 二、常用文件 1.文件夹XXX_Data 2.文件夹MonoBleedingEdge 3.文件夹XXX_Data内部 三、文件的应用 1.如果你替换了一个图片 2.如果你新增了或减少了图片和资源 3.场景中有变动 4.resources代码加载的资源改了 5.如果你代码替换了 四、作…...

编程日记 2024/6/14 10:09:05

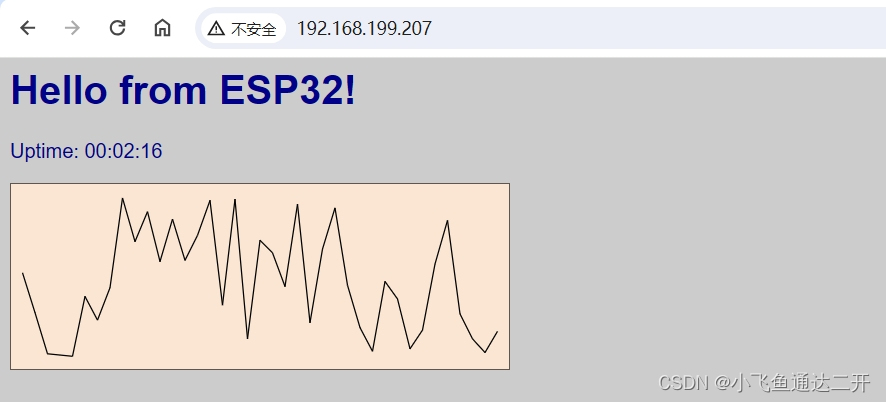
【Ardiuno】实验使用ESP32单片机实现高级web服务器暂时动态图表功能（图文）

接下来&#xff0c;我们继续实验示例代码中的Wifi“高级web服务器”&#xff0c;配置相关的无线密码后&#xff0c;开始实验 #include <WiFi.h> #include <WiFiClient.h> #include <WebServer.h> #include <ESPmDNS.h>const char *ssid "XIAOFE…...

编程日记 2024/6/14 10:07:01

深入浅出服务网格（Service Mesh）：现代微服务架构的护航者

什么是服务网格&#xff1f; 服务网格是一种专用于处理微服务间通信的基础设施层&#xff0c;通常以轻量级代理&#xff08;sidecar&#xff09;的形式部署在每个服务实例旁边。它主要负责以下几项任务&#xff1a; 服务发现&#xff1a;自动检测和注册服务实例&#xff0c;使…...

编程日记 2024/6/14 10:06:00

node调试

vscode安装插件&#xff1a;JavaScript Debugger (Nightly) 点击后生成一个launch.json文件 打断点&#xff0c;并发送一个请求来执行代码到断点处 按右上的向下箭头&#xff0c;进入源码&#xff0c;进行查看&#xff0c;左边查看变量等值...

编程日记 2024/6/14 10:03:57

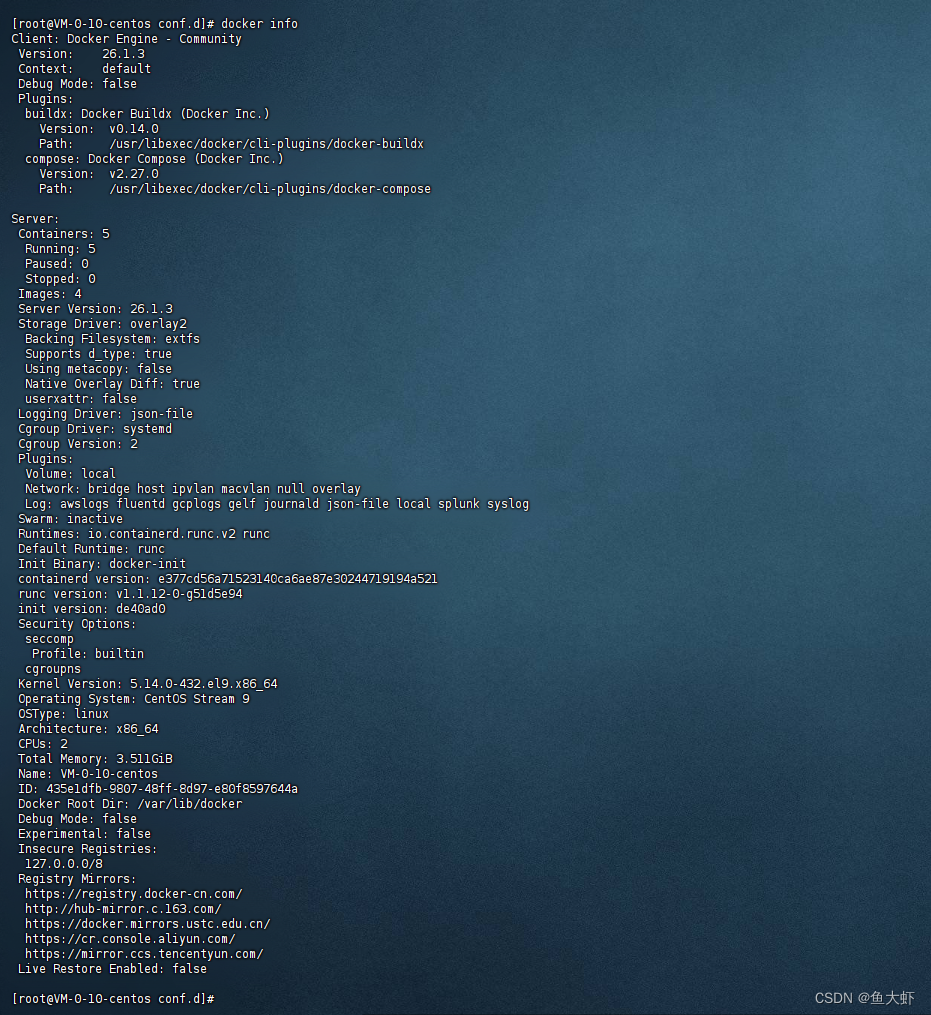
docker拉取镜像失败超时的解决方法,docker配置国内镜像源

更换国内源 创建或修改 /etc/docker/daemon.json 文件 安装docker后一般只有 /etc/docker 这个目录 下面并没有 daemon.json 文件 我们直接创建 &#xff1a; vim /etc/docker/daemon.json {"registry-mirrors" : ["https://registry.docker-cn.com"…...

编程日记 2024/6/14 10:00:54

建造气膜结构体育馆需要注意的事项—轻空间

气膜结构体育馆以其快速建造、低成本、灵活性高等优势&#xff0c;越来越受到各类运动场所的青睐。气膜结构利用空气压力支撑膜材&#xff0c;从而形成自持结构&#xff0c;无需传统的钢筋混凝土框架。这类建筑适用于各种气候条件&#xff0c;且可根据需要快速搭建和拆卸。然而…...

编程日记 2024/6/14 9:58:48

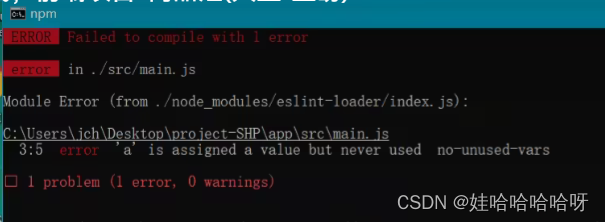
使用脚手架创建vue2项目（关闭eslint语法检查 、运行项目时自动打开网址、src文件夹简写方法）

使用脚手架创建vue2项目会默认安装的插件&#xff08;eslint) 这个插件是检查语法的。 假设我们在main.js中定义了一个变量&#xff0c;没有使用 eslint 就会检测出错误 &#xff08;事实是我们并没有写错而是eslint 给我们判断是错的&#xff0c;所以这样会很麻烦&#xff…...

编程日记 2024/6/14 9:57:45

Vim 调用外部命令学习笔记

Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

编程新知 2025/11/16 8:24:16

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

ES6从入门到精通：前言

ES6简介 ES6&#xff08;ECMAScript 2015&#xff09;是JavaScript语言的重大更新&#xff0c;引入了许多新特性&#xff0c;包括语法糖、新数据类型、模块化支持等&#xff0c;显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var&#xf…...

编程新知 2025/8/18 16:42:44

ESP32读取DHT11温湿度数据

芯片&#xff1a;ESP32 环境&#xff1a;Arduino 一、安装DHT11传感器库 红框的库&#xff0c;别安装错了 二、代码 注意&#xff0c;DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

编程新知 2026/1/30 8:46:45

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

HTML前端开发：JavaScript 常用事件详解

作为前端开发的核心&#xff0c;JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例&#xff1a; 1. onclick - 点击事件 当元素被单击时触发&#xff08;左键点击&#xff09; button.onclick function() {alert("按钮被点击了&#xff01;&…...

编程新知 2025/11/10 10:45:11

九天毕昇深度学习平台 | 如何安装库？

pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子&#xff1a; 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

编程新知 2026/1/31 2:13:57

让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中&#xff0c;损失函数的选择对模型性能具有决定性影响。均方误差&#xff08;MSE&#xff09;作为经典的损失函数&#xff0c;在处理干净数据时表现优异&#xff0c;但在面对包含异常值的噪声数据时&#xff0c;其对大误差的二次惩罚机制往往导致模型参数…...

编程新知 2026/1/28 2:18:46

Docker 本地安装 mysql 数据库

Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker &#xff1b;并安装。 基础操作不再赘述。 打开 macOS 终端&#xff0c;开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

编程新知 2026/2/6 21:43:26