【数据结构(邓俊辉)学习笔记】图03——拓扑排序
文章目录
- 0. 概述
- 1. 零入度算法
- 1. 1 拓扑排序
- 1. 2 算法
- 2. 零出度算法
- 2.1 算法
- 2.2 实现
- 2.3. 复杂度
0. 概述
学习下拓扑排序
1. 零入度算法
1. 1 拓扑排序
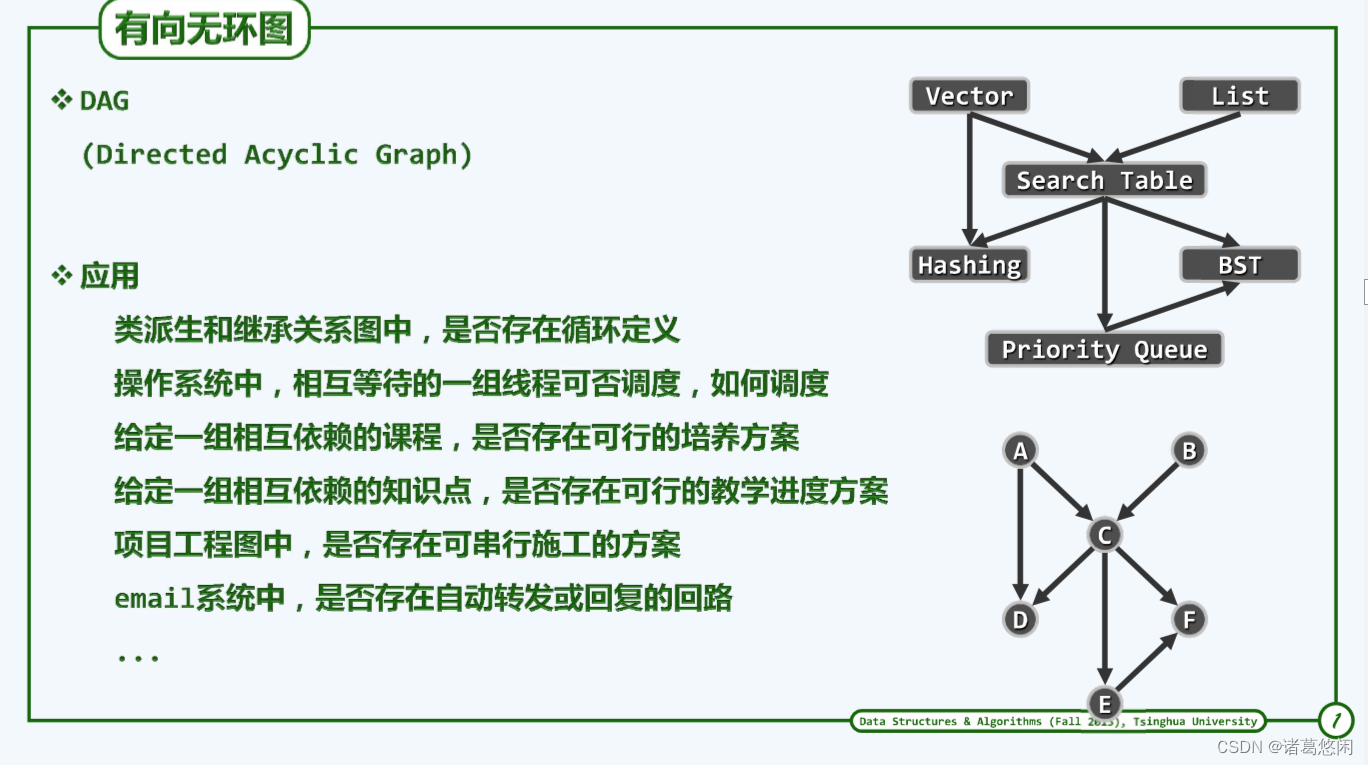
首先理解下拓扑排序
其实老师经常干这事,如编讲义,将已经知道的知识点串起来变成讲课序列。那怎么串起来呢?将知识点列出,将它们之间的相互关系描述下。要讲priority queue那上一讲需要讲什么内容,要讲hashing需要讲哪些内容,需要罗列出来。但是讲课不可能像分支一样平行一分为二裂开,最终都会变成下面这样平坦的线性序列。

(续)一个好的安排是什么呢?每当讲到一个知识点时,它所依赖的知识点都应该在此前依然讲过,这样就会变成一个线性序列。将原来图中所有的点整理成这样一个线性次序,前面点与后面点的边次序都是前指向后,没有后指向前,这就是对原图的拓扑排序。
1. 2 算法
- 如果真有这么一个图,怎么排呢?

因为这个图有依赖关系,所以是不折不扣的有向图,但有意思的是这里不能有环,如果有环路就有问题。

首先需要找到零入度的点——无任何依赖,在dag图中必然有这么一个点,由于DAG子图亦为DAG,于是可以利用减而治之思想,将这个零入度的点抹掉,接着找下一个零入度点。
- 那么这个算法如何实现?

图中已经有零入度的点A或B,任取一个,这里取A,放入队列中,等价将A点及其边从图中删除。由于DAG的子图亦是DAG,所以还会有零入度的点,将B点放入队列中,然后依次类推,当所有的点都放入队列后,队列中的节点顺序就是拓扑排序。
但这个方法并不好,实现起来比较麻烦,需要每次去找那个零入度的点,而且删除点及其边的时候还要更新相应信息,可能会对图产生伤害,那怎么做呢?看下下面的零出度算法
2. 零出度算法
2.1 算法
说服下自己,DAG既有零入度点也有零出度点,这个很重要,为什么这么讲,因为之前的DFS(深度优先搜索)可以帮我们实现这个方法。
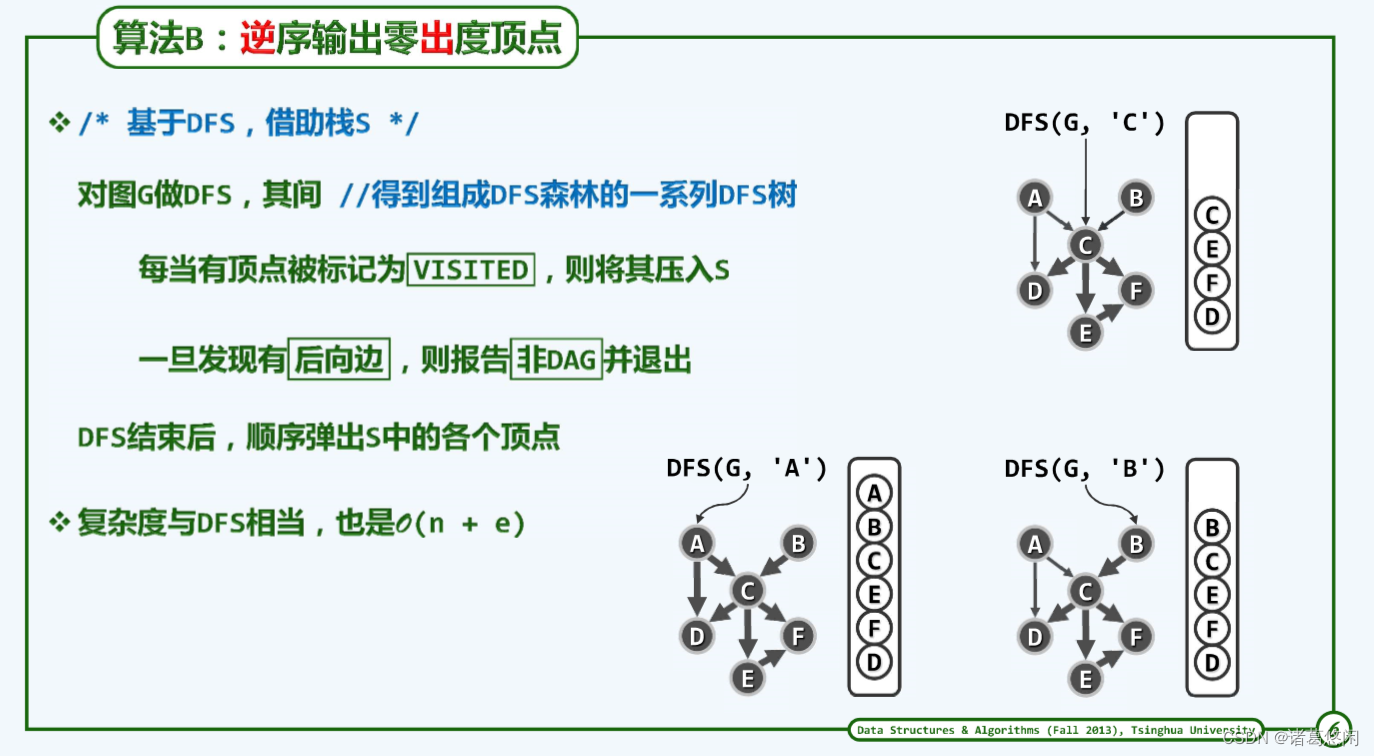
这样要做的事就比较简单,不需要零入度算法那这样改改度数等等。之前已经造出DFS算法,这样就可以搭DFS便车实现零出度算法。
如何实现呢?
2.2 实现

这里引入一个栈,排序结果将以逆序打印出来。随便找一个点,这里首先访问顶点V,将顶点V状态初始值设置为DISCOVERED,接着枚举V的所有邻居,视u的状态,分别处理,后续会做分析。访问所有邻居后,将顶点V的状态设置为VISITED,然后顶点V入栈。
接着还有顶点V的邻居处理方法还未做交代,怎么处理呢?

- 若顶点U的状态为UNDISCOVERED,更新顶点U的父亲为V,边的状态为TREE,作递归调用,从顶点u处深入。
- 顶点U的状态为DISCOVERED,一旦发现后向边,即图非DAG图,无拓扑排序,则退出而不再深入。
- 顶点U的状态为VISITED,更新下顶点状态。
2.3. 复杂度
这里仅额外引入的栈,规模不超过顶点总数O(n)。总体而言,空间复杂度与基本的深度优先搜索算法同样,仍为O(n + e)。该算法的递归跟踪过程与标准DFS搜索完全一致,且各递归实例自身的执行时间依然保持为O(1),故总体运行时间仍为O(n + e)。
相关文章:

【数据结构(邓俊辉)学习笔记】图03——拓扑排序
文章目录 0. 概述1. 零入度算法1. 1 拓扑排序1. 2 算法 2. 零出度算法2.1 算法2.2 实现2.3. 复杂度 0. 概述 学习下拓扑排序 1. 零入度算法 1. 1 拓扑排序 首先理解下拓扑排序 其实老师经常干这事,如编讲义,将已经知道的知识点串起来变成讲课序列。那…...

C#参数使用场景简要说明
C#参数使用场景简要说明 1、传值参数 方法、类成员的初始化 2、输出参数 方法返回值不能满足,需要多个返回值时; 3、引用参数 方法需要修改变量需带回原变量时; 4、具名参数 代码可读性高,参数可交换位置 5、方法扩展(…...

线性代数|机器学习-P10最小二乘法的四种方案
文章目录 1. 概述2. SVD奇异值分解3. 最小二乘法方程解4. 最小二乘法图像解释5. Gram-Schmidt 1. 概述 当我们需要根据一堆数据点去拟合出一条近似的直线的时候,就会用到 最小二乘法 .根据矩阵A的情况,有如下四种方法 在r n m 时,SVD奇异…...
【Android面试八股文】你能描述一下JVM中的类加载过程吗?
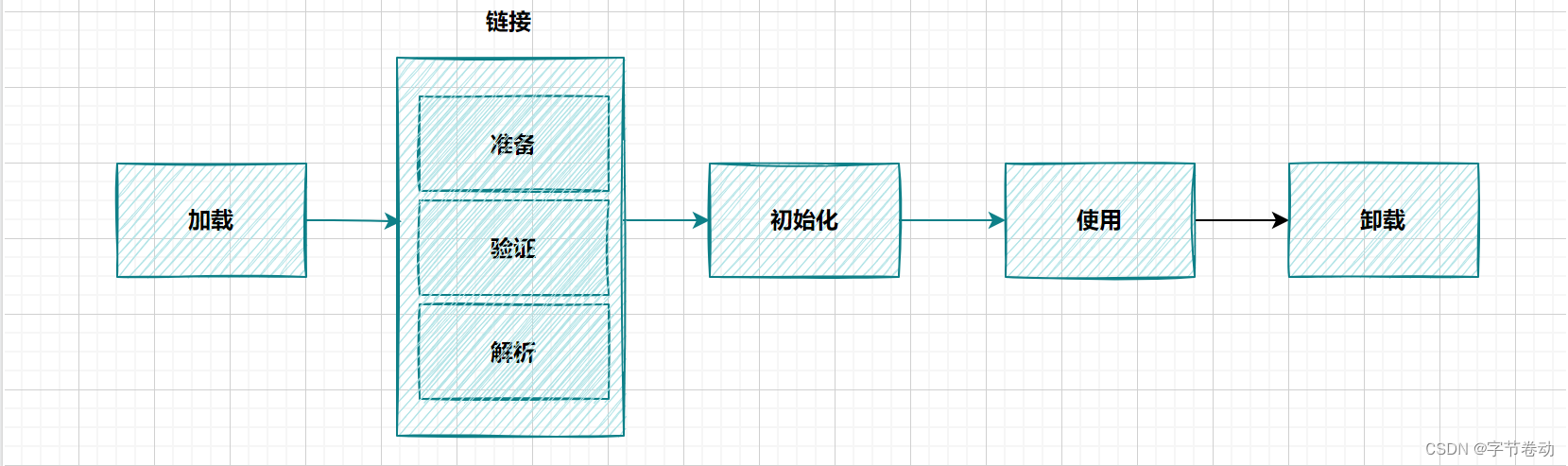
文章目录 一、Java类的生命周期二、JVM类加载过程1. 加载(Loading)2. 链接(Linking)a. 验证(Verification)b. 准备(Preparation)b.1 准备阶段的初始值b.2 用户定义的初值b.3 常量的初始化c. 解析(Resolution)3. 初始化(Initialization)3.1 什么是 `<clinit>`…...
MYSQL八、MYSQL的SQL优化
一、SQL优化 sql优化是指:通过对sql语句和数据库结构的调整,来提高数据库查询、插入、更新和删除等操作的性能和效率。 1、插入数据优化 要一次性往数据库表中插入多条记录: insert into tb_test values(1,tom); insert into tb_tes…...

鸿蒙轻内核M核源码分析系列二一 02 文件系统LittleFS
1、LFS文件系统结构体介绍 会分2部分来介绍结构体部分,先介绍LittleFS文件系统的结构体,然后介绍LiteOS-M内核中提供的和LittleFS相关的一些结构体。 1.1 LittleFS的枚举结构体 在openharmony/third_party/littlefs/lfs.h头文件中定义LittleFS的枚举、…...

【ARMv8/ARMv9 硬件加速系列 3 -- SVE 指令语法及编译参数详细介绍】
文章目录 SVE 汇编语法SVE 单通道谓词SVE 测试代码 SVE 软件和库支持SVE 编译参数配置-marcharmv8-alseprofilememtagsve2-aessve2-bitpermcryptosve2sve2-sha3sve2-sm4 SVE 汇编语法 在介绍 SVE 汇编指令语法之前,先介绍下如何判断自己所使用的芯片是否实现了SVE功…...

Java版+ SaaS应用+接口技术RESTful API 技术开发的智慧医院HIS系统源码 专注医院管理系统研发 支持二开
Java版 SaaS应用接口技术RESTful API WebSocket WebService技术开发的智慧医院HIS系统源码 专注医院管理系统研发 支持二开 医院住院管理系统(Hospital Information System简称HIS)是一门医学、信息、管理、计算机等多种学科为一体的边缘科学ÿ…...

工业机器人远程运维,增强智慧工厂运营管理
1、需求背景 随着工业自动化技术的普及和工业机器人应用的增加,制造业对于生产线稳定性和效率的要求不断提高。然而,传统的现场监控方式存在着地理位置限制、实时监控难度大以及诊断能力有限等问题,迫切需要一种更具灵活性和效率的监控方式。…...

理解Python的元类
1.type()函数 type 函数是一个内置函数,用来获取一个对象的类型。它可以接受一个参数,返回这个参数的数据类型。type也可以用来创建类,type就是元类 x333 list["ab"] tuple (1, "a", True, 3.14) dict {name: Alice,…...

web前端黑马下载:探索学习资源的海洋
web前端黑马下载:探索学习资源的海洋 在数字化时代,Web前端技术日益成为互联网行业的核心驱动力。为了跟上这一趋势,众多学习者纷纷投身于Web前端的学习之中。而在这个过程中,“黑马”作为一个备受瞩目的品牌,其Web前…...

最新版jd-gui下载
对于java开发的工程师来说,jd-gui应该是经常会用到的工具了 官网的jd-gui目前只支持到JAVA13,更新版本JAVA编译出来的JAR包就反编译不出来了 此版本支持到了JAVA23 如果需要win以外的其他版本,可以查看我的其他上传 如果不想花积分&#…...
FPGA时钟--->(001)时钟介绍)
(051)FPGA时钟--->(001)时钟介绍
(001)时钟介绍 1 目录 (a)FPGA简介 (b)Verilog简介 (c)时钟简介 (d)时钟介绍 (e)结束 1 FPGA简介 (a)FPGA(Field Programmable Gate Array)是在PAL (可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电…...

Java程序员英语单词通关:
Java程序员英语单词通关: abstract - 抽象的 boolean - 布尔值 break - 打断 byte - 字节 case - 情况,实例 catch - 捕获 char - 字符 class - 类 continue - 继续 default - 默认,通常 do - 做,运行 double - 双精度…...

数据库开发-Mysql03
目录 1. 多表查询 1.1 概述 1.1.1 数据准备 1.1.2 介绍 1.1.3 分类 1.2 内连接 1.3 外连接 1.4 子查询 1.4.1 介绍 1.4.2 标量子查询 1.4.3 列子查询 1.4.4 行子查询 1.4.5 表子查询 1.5 案例 2. 事务 2.1 介绍 2.2 操作 2.3 四大特性 3. 索引 3.1 介绍 3…...
)
0-1 背包问题(动态规划 查询背包元素)
描述 给定n种物品和一个背包,物品i的重量是Wi,其价值为Vi,问如何选择装入背包的物品,使得装入背包的物品的总价值最大? 在选择装入背包的物品时,对每种物品i只能有两种选择,装入或者不装入…...

elasticsearch快照生成与恢复
Elasticsearch快照生成与恢复的场景主要涉及到数据的备份与恢复需求。当需要对Elasticsearch集群中的数据进行备份,或者在数据丢失、损坏等情况下需要恢复数据时,就可以使用快照功能。 快照生成的方法通常包括以下步骤: 1、创建一个快照仓库…...
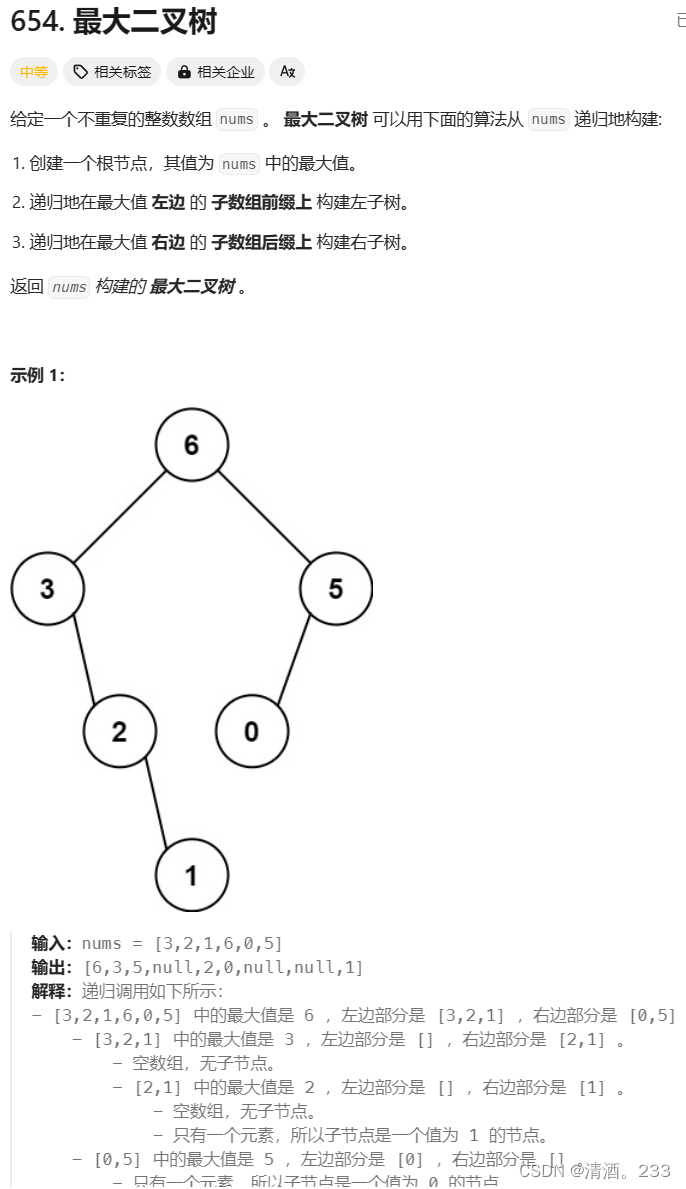
178.二叉树:最大二叉树(力扣)
代码解决 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* Tre…...
跨境电商中的IP隔离是什么?怎么做?
一、IP地址隔离的概念和原理 当我们谈论 IP 地址隔离时,我们实际上是在讨论一种网络安全策略,旨在通过技术手段将网络划分为不同的区域或子网,每个区域或子网都有自己独特的 IP 地址范围。这种划分使网络管理员可以更精细地控制哪些设备或用…...
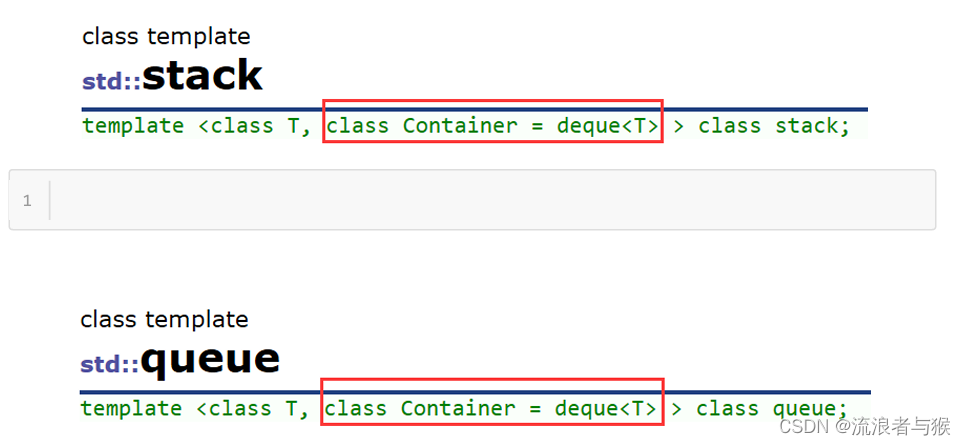
【C++】stack、queue和deque的使用
💗个人主页💗 ⭐个人专栏——C学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 导读 一、stack 1. stack介绍 2. stack使用 二、queue 1. queue介绍 2. queue使用 三、deque 1. deque介绍 2. deque的…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
