了解统计学中不同类型的分布
目录
一、说明
二、均匀分布:
三、机器学习和数据科学中的均匀分布示例:
3.1 对数正态分布:
3.2 机器学习和数据科学中的对数正态分布示例:
四、 帕累托分布
4.1 什么是幂律?
4.2 机器学习和数据科学中的帕累托分布示例:
4.3 伯努利分布:
4.4 机器学习和数据科学中的伯努利分布示例:
4.5. 二项分布:
4.6 机器学习和数据科学中的二项分布示例:
五、概率分布变换:
5.1. 统计假设
5.2. 提高算法性能
5.3. 稳定方差
5.4. 减少偏斜
5.5 实现常态的常见转换
一、说明
统计学是理解数据的有力工具,其核心在于分布的概念。统计学中的分布有助于我们理解数据的分布方式,为各种数据集的概率和行为提供重要的见解。从熟悉的钟形曲线的正态分布到其他偏斜和重尾模式,本博客旨在解开不同类型的分布,清楚地了解它们在统计分析中的特征、应用和意义。

二、均匀分布:
均匀分布是一种概率分布,其中所有结果在给定范围内的可能性相同。这意味着,如果要从此范围中选择一个随机值,则任何值都与任何其他值一样可能。例如,从一篮子苹果中随机选择的苹果的重量在 100 到 200 克之间,将遵循连续的均匀分布。
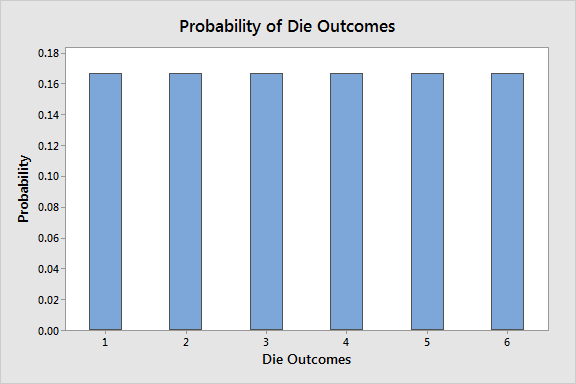
骰子结果的离散均匀分布
连续均匀分布的概率密度函数为:

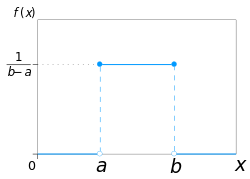
均匀分布的CDF由下式给出:
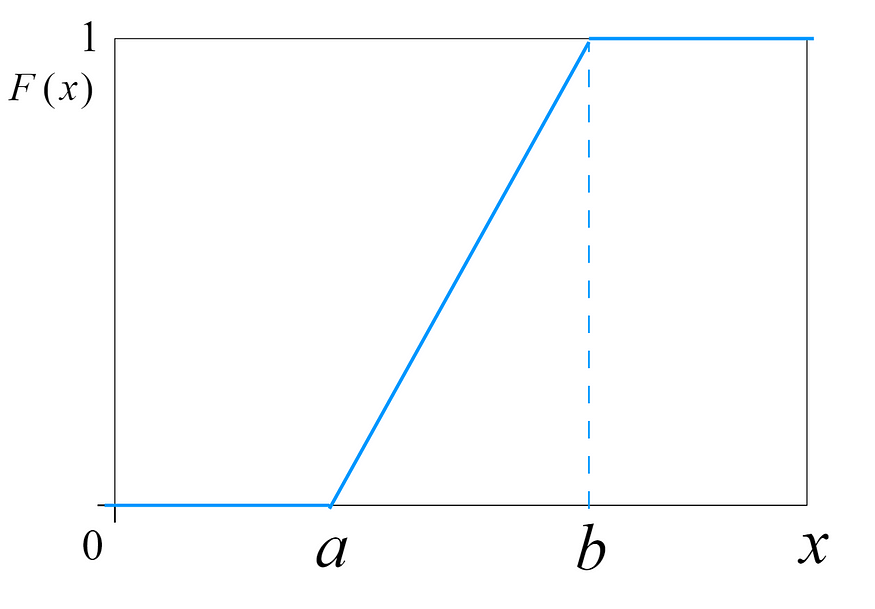
均匀分布图中不存在偏度。
三、机器学习和数据科学中的均匀分布示例:
- 随机初始化:在许多机器学习算法中,例如神经网络和 k 均值聚类,参数的初始值可能会对最终结果产生重大影响。均匀分布通常用于随机初始化参数,因为它可以确保范围内的所有值都具有相等的选择
概率。 - 采样:均匀分布也可用于采样。例如,如果数据集中每个类的样本数相等,则可以使用均匀分布随机选择代表所有类的数据子集。
- 数据增强:在某些情况下,您可能希望通过生成与原始数据相似的新示例来人为地增加数据集的大小。均匀分布可用于生成原始数据指定范围内的新数据点。
- 超参数优化:均匀分布也可用于超参数优化,在超参数优化中,您需要为机器学习模型搜索超参数的最佳组合。通过为每个超参数定义均匀的先验分布,可以从分布中采样以探索超参数空间。
3.1 对数正态分布:
在概率论和统计学中,对数正态分布是对数呈正态分布的随机变量的重尾连续概率分布,即,如果取每个值的自然对数并绘制此分布,则得到正态分布。 对数正态的PDF方程由下式给出:

这种分布是右偏的,因为它倾向于在右侧产生更长的尾部,这意味着大多数数据点集中在左侧,少数较大的值延伸到右侧。

对数正态的概率分布

对数正态的累积分布
3.2 机器学习和数据科学中的对数正态分布示例:
- 在 Internet 论坛中发布的评论长度遵循对数正态分布。
- 用户在在线文章(笑话、新闻等)上的停留时间遵循对数正态分布。
- 国际象棋比赛的长度往往遵循对数正态分布。
在经济学中,有证据表明 97%-99% 的人口的收入是按对数正态分布的。
四、 帕累托分布
帕累托分布是一种概率分布,通常用于模拟财富、收入和其他表现出类似幂律行为的量的分布。
4.1 什么是幂律?
在数学中,幂律是两个变量之间的函数关系,其中一个变量与另一个变量的幂成正比。具体来说,如果 y 和 x 是幂律相关的两个变量,则关系可以写为:
y = k * x^a
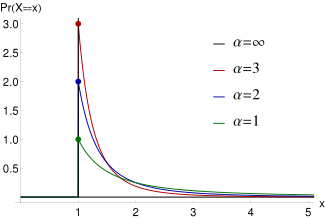
帕累托分布的概率分布

维尔弗雷多·帕累托(Vilfredo Pareto)最初使用这种分布来描述个人之间的财富分配,因为它似乎很好地表明了任何社会财富的很大一部分由该社会中较小比例的人拥有的方式。他还用它来描述收入分配。这个想法有时更简单地表达为帕累托原则或“80-20规则”,即20%的人口控制着80%的财富。
4.2 机器学习和数据科学中的帕累托分布示例:
- 人类住区的规模(少数城市,/村庄)。
- 使用 TCP 协议的 Internet 流量的文件大小分布(许多较小的文件,少数较大的文件)
4.3 伯努利分布:
伯努利分布是一种对二元结果进行建模的概率分布,其中结果可以是成功(由值 1 表示)或失败(由值 0 表示)。伯努利分布的特征是单个参数,即成功概率,用 p 表示。

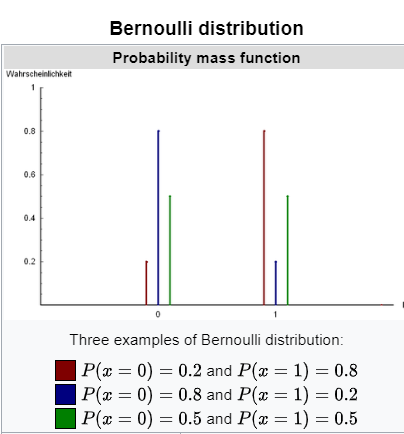
4.4 机器学习和数据科学中的伯努利分布示例:
伯努利分布通常用于机器学习中,用于对二元结果进行建模,例如客户是否会购买,电子邮件是否为垃圾邮件,或者患者是否患有某种疾病。
4.5. 二项分布:
二项分布是一种概率分布,它描述了在固定数量的独立伯努利试验中的成功次数,该试验具有两种可能的结果(通常称为“成功”和“失败”),其中每个试验的成功概率是恒定的。二项分布由两个参数表征:试验次数 n 和成功概率 p。

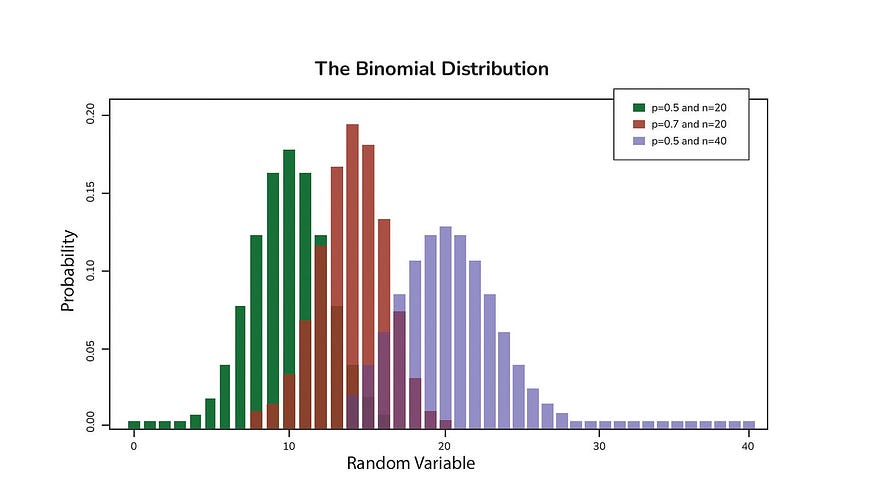
4.6 机器学习和数据科学中的二项分布示例:
- 模型精度:在测试预测电子邮件是否为垃圾邮件的机器学习模型时,可能会运行它 100 次。每次,您都会检查它是否正确(成功)或不正确(失败)。二项分布可帮助您了解在给定一定准确率的情况下,模型可能正确预测的次数为 100 次。
- A/B 测试:在 A/B 测试中,您可以比较某些内容的两个版本(例如网站或广告),看看哪个版本效果更好。通过二项分布,您可以根据一定的成功概率来估计一个版本更成功的频率,例如获得更多点击或转化。
五、概率分布变换:
在分布方面,变换是指将数学函数应用于数据以改变其底层分布的过程。分布描述了数据如何分布在一系列值中,转换用于实现各种目标,包括修改分布的形状、比例或分布。
当您需要使用假定正态分布的算法时,变换在统计学和机器学习中可能至关重要。许多统计方法和机器学习算法在数据遵循正态分布时表现最佳,这要归功于对称性、定义的均值和标准差以及一致的分布等特性。
以下是应用转换使数据更正态分布的一些原因:
5.1. 统计假设
统计检验(如 t 检验、方差分析和许多回归模型)假定基础数据或残差(误差)呈正态分布。当数据不符合此假设时,结果可能会有偏见或具有误导性。转换有助于确保数据符合这些假设。
5.2. 提高算法性能
机器学习算法,特别是线性回归和逻辑回归,在数据或残差呈正态分布时可能表现更好。这是因为这些算法所依据的假设与正态性密切相关。通过转换使数据分布更均匀,可以提高算法的预测准确性并减少偏差。
5.3. 稳定方差
当数据具有不稳定的方差(异方差)时,可能会导致建模错误,并降低期望一致方差的算法的有效性。转换有助于稳定方差,使其在不同范围的数据中更加恒定。
5.4. 减少偏斜
有偏差的数据可能导致不准确的结论,并使结果的解释复杂化。期望对称数据的算法在偏斜输入时可能表现不佳。对数转换等转换可以减少偏度,使数据更接近正态分布。
5.5 实现常态的常见转换
以下是一些用于使数据更正态分布的常见转换:
- 日志转换:通过采用自然对数来转换数据,从而减少正偏度。对于具有指数增长或长右尾的数据很有用。
我在泰坦尼克号数据集上详细应用了日志转换。你可以从这里学习代码和概念!
- 平方根变换:通过取平方根来转换数据以减少偏度,通常用于计数数据或方差随均值增加的数据。
- Box-Cox 变换:一种灵活的电源转换,可以将一系列非正态数据转换为更正态分布。它需要非负数据,并确定最佳功率变换参数 (λ) 以实现正态性。它可以在数学上表示为:

学习代码,你可以从这里学习代码和概念!
- 相互转化:涉及采用倒数 (1/x) 来转换数据,从而减少正偏度。
希望这篇博客能加深你对统计学中不同概率分布的理解。如果您发现此内容的价值,请考虑关注我以获取更有见地的帖子。谢谢!感谢您花时间阅读本文。
相关文章:

了解统计学中不同类型的分布
目录 一、说明 二、均匀分布: 三、机器学习和数据科学中的均匀分布示例: 3.1 对数正态分布: 3.2 机器学习和数据科学中的对数正态分布示例: 四、 帕累托分布 4.1 什么是幂律? 4.2 机器学习和数据科学中的帕累托分布示例…...

k8s-CCE创建工作负载变量引用
CCE创建工作负载变量引用 背景,看到cce创建负载时会生成变量,如下。在skywaking-agent的使用,想要调用cce负载变量生成service_name。 -Dskywalking.agent.authentication里含有敏感信息需要写到配置项。简单粗糙的都写到配置项好像不合适。…...

后端主流框架--Spring02
前言:上篇关于Spring的文章介绍了一些Spring的基本知识,此篇文章主要分享一下如何配置Spring环境,如何注入等。 Spring项目构建 导入Spring相关JAR包 <dependency><groupId>org.springframework</groupId><artifactId>spring…...

[数据集][目标检测]减速带检测数据集VOC+YOLO格式5400张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):5400 标注数量(xml文件个数):5400 标注数量(txt文件个数):5400 标注…...

分析Linux操作指令及使用场景与频率分析 持续更新
本篇主要针对在日常工作与学习中使用较多的linux指令的使用方法以及使用频次进行分析与讲解,旨在能够更好的掌握这些必备的技能。 linux指令非常的多,如果要记住所有的指令使用方法是非常困难的且要花费很长的时间,很多人习惯离开使用去通篇…...
)
Redis 字符串(String)
Redis 字符串(String) 介绍 Redis是一种开源的、高性能的键值数据库,它支持多种类型的数据结构,其中字符串(String)是Redis中最基本的数据类型之一。字符串类型可以存储任何形式的字符串,包括文本、序列化的对象或二进制数据。在Redis中,字符串类型的最大容量为512MB。 …...

第一篇:容器化的未来:从Docker的革命到云原生架构
容器化的未来:从Docker的革命到云原生架构 1. 引言 在当今快速演进的技术领域,容器化技术已经成为云计算和微服务架构的重要组成部分。该技术以其高效的资源利用率、快速的部署能力和卓越的隔离性能,彻底改变了软件开发和部署的方式。容器化…...
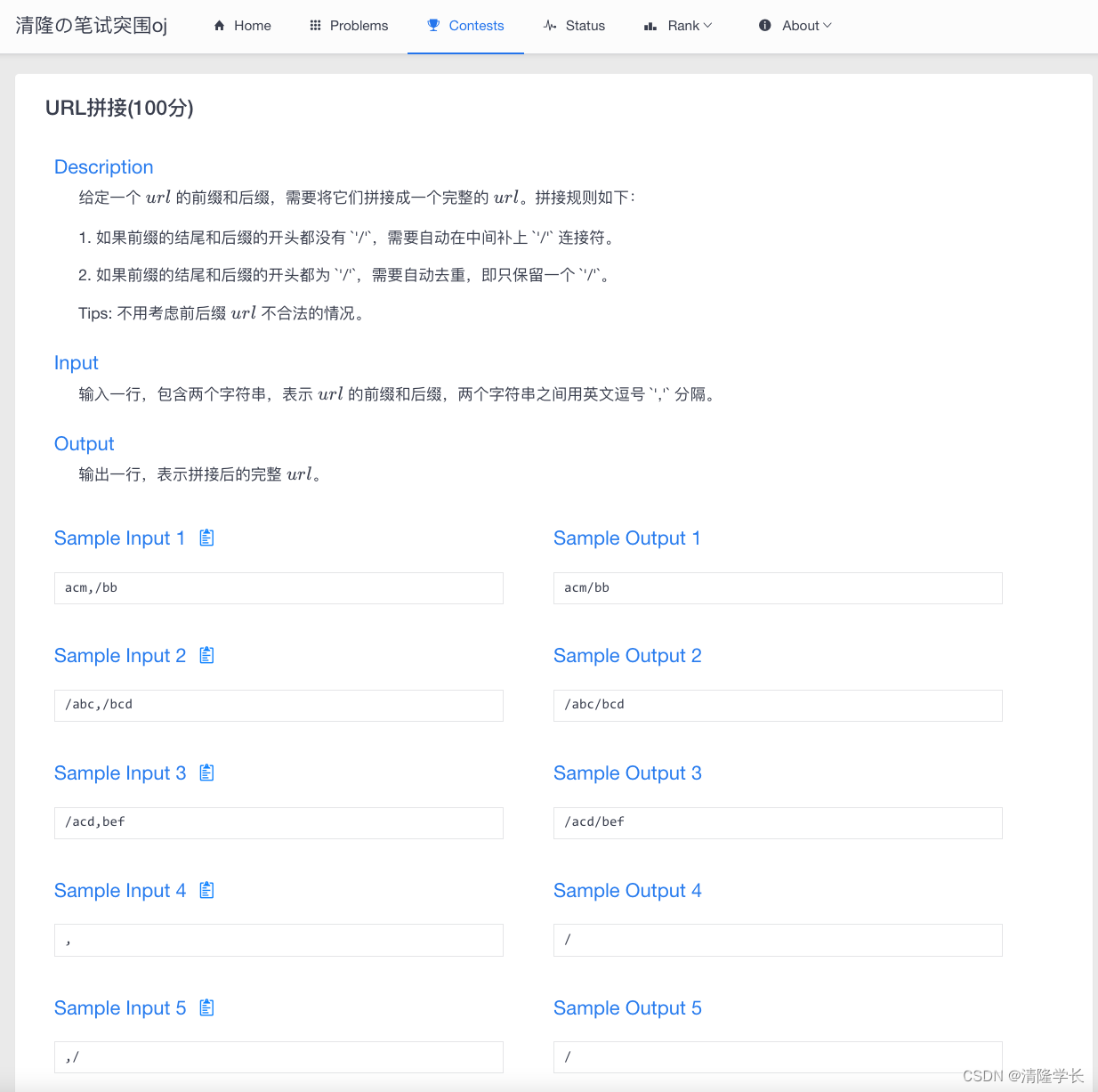
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] URL拼接(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 URL拼接(100分) 🌍 评测功能需要订阅专栏后私信联系清隆解…...

反射,枚举以及lambda表达式
【本节目标】 1. 掌握反射 2. 掌握枚举 3. 掌握lambda表达式使用 反射 1 定义 Java的反射(reflection)机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法;对于任意一个对象,都能够调…...

DNS域名解析----分离解析、多域名解析、父域与子域
1 理论部分 1.1 分离解析 DNS的分离解析,是指根据不同的客户端提供不同的域名解析记录。来自不同地址的客户机请求解析同一域名时,为其提供不同的解析结果。也就是内外网客户请求访问相同的域名时,能解析出不同的IP地址,实现负载…...

Spring底层架构核心概念解析
BeanDefinition BeanDefinition表示Bean定义,BeanDefinition中存在很多属性用来描述一个Bean的特点.比如: beanClass:表示Bean类型scope:表示Bean作用域,单例/原型等lazyInit:表示Bean是否懒加载initMethodName:表示Bean初始化时要执行的方法destoryMethodName:表示Bean销毁时…...

C++ 44 之 指针运算符的重载
#include <iostream> #include <string> using namespace std;class Students04{ public:int m_age;Students04(int age){this->m_age age;}void showAge(){cout << "年龄是: " << this->m_age << endl;}~Students0…...

onlyoffice在线预览加载优化
背景: 使用容器部署onlyoffice到linux服务器,使用内网访问速度还可以接受,但是如果放到外网路径访问起来,速度就会很慢,甚至加载失败; 优化方案: 预览的过程排除网络因素,可以发现打…...

依赖自动装配
黑马程序员SSM框架 文章目录 1、依赖自动装配2、依赖自动装配的特征 1、依赖自动装配 IoC容器根据bean所依赖的资源在容器中自动查找并注入到bean中的过程称为自动装配自动装配方式 按类型(常用)按名称按构造方法不启用自动装配 配置中使用bean标签auto…...
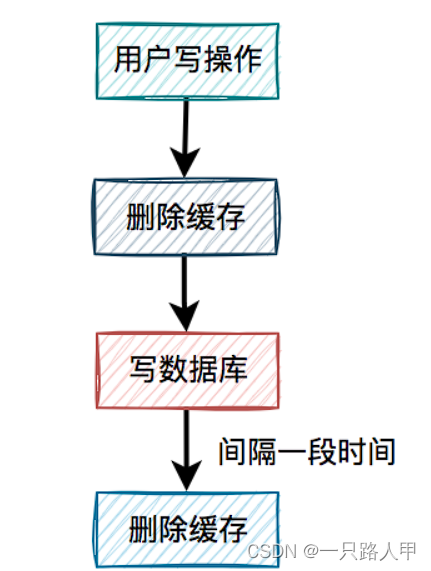
mysql和redis的双写一致性问题
一,使用方案 在使用redis作为缓存的场景下,我们一般使用流程如下 二,更新数据场景 我们此时修改个某条数据,如何保证mysql数据库和redis缓存中的数据一致呢? 按照常规思路有四种办法,1.先更新mysql数据&a…...
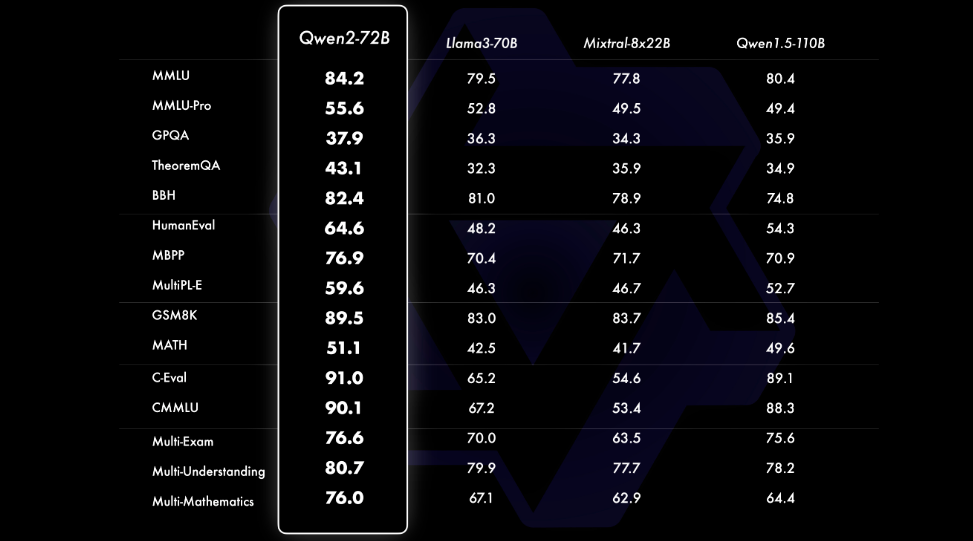
Qwen2——阿里巴巴最新的多语言模型挑战 Llama 3 等 SOTA
引言 经过几个月的期待, 阿里巴巴 Qwen 团队终于发布了 Qwen2 – 他们强大的语言模型系列的下一代发展。 Qwen2 代表了一次重大飞跃,拥有尖端的进步,有可能将其定位为 Meta 著名的最佳替代品 骆驼3 模型。在本次技术深入探讨中,我…...

等级考试3-2021年3月题
作业: #include <iostream> using namespace std; int chonghe(int,int,int,int); int main(){int a[1000],b[1000];int n,ma0;cin>>n;for(int i0;i<n;i){cin>>a[i]>>b[i];}for(int i0;i<n;i){for(int ji1;j<n;j){mamax(ma,chongh…...

Web前端开发PPT:深入探索与实战应用
Web前端开发PPT:深入探索与实战应用 在数字化时代,Web前端开发已成为构建丰富、交互性强的网页应用的关键环节。本次分享旨在通过PPT的形式,带领大家深入探索Web前端开发的精髓,并分享一些实战应用的经验。接下来,我们…...

liunx常见指令
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 二、安装环境 1.租借服务器 2.下载安装 XShell 3.使用xshll登录服务器 三、Linux基础命令 一、文件和命令 编辑1、cd 命令 2、pwd 命令 3、ls 命令 4、cp 命令 …...

vscode设置成中文界面
在Visual Studio Code(VSCode)中设置中文界面,你可以采用以下几种方法,以下是详细步骤: 方法一:通过设置菜单设置中文 打开VSCode:首先,确保你已经打开了VSCode软件。进入设置&…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
