期权无风险套利(Risk-Free Arbitrage)举例以及期权无套利定价公式
期权市场的无风险套利
中文版
期权市场中的套利实例
为了清楚地说明,让我们通过一个现实的例子来展示套利。
期权市场中的套利实例
假设市场上有以下价格:
- 标的股票价格:100美元
- 欧式看涨期权(行权价100美元,3个月到期):8美元
- 欧式看跌期权(行权价100美元,3个月到期):5美元
- 无风险利率:2%(年化)
我们使用一个经典的套利策略,称为“转换套利”:
转换套利策略
转换套利涉及买入标的股票、买入看跌期权并卖出看涨期权。如果期权与标的股票之间存在定价错误,此策略可以锁定无风险利润。
逐步过程:
-
买入标的股票:
- 以100美元购买1股XYZ公司股票。
-
买入欧式看跌期权:
- 以5美元购买一个行权价为100美元的看跌期权。
-
卖出欧式看涨期权:
- 以8美元卖出一个行权价为100美元的看涨期权。
总初始投资:
- 购买股票:100美元
- 购买看跌期权:5美元
- 卖出看涨期权:-8美元(你收到8美元)
总初始投资 = 100美元(股票) + 5美元(看跌期权) - 8美元(看涨期权) = 97美元
到期时的收益:
无论股票价格在到期时是多少,你的头寸都是对冲的:
-
如果股票价格高于100美元(例如110美元):
- 看跌期权作废。
- 看涨期权被执行,你以100美元卖出股票。
- 你收到100美元。
-
如果股票价格低于100美元(例如90美元):
- 看跌期权被执行,你以100美元卖出股票。
- 看涨期权作废。
- 你收到100美元。
在这两种情况下,你到期时都得到100美元。
利润计算:
- 到期时收到的总金额:100美元
- 总初始投资:97美元
利润 = 100美元 - 97美元 = 3美元
这是由于期权相对于标的股票的初始定价错误而获得的无风险利润3美元。
无套利例子
在一个无套利市场中,不会存在这样的差异。看涨期权和看跌期权的价格会与股票价格和无风险利率对齐,以便上述策略不会产生无风险利润。
无套利条件下的期权定价实际例子
在无套利条件下,期权的价格应该符合以下无套利定价公式:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
其中:
- ( C ) 是看涨期权的价格
- ( P ) 是看跌期权的价格
- ( S ) 是股票价格
- ( K ) 是行权价
- ( r ) 是无风险利率
- ( t ) 是到期时间
实例说明
假设以下市场条件:
- 标的股票价格(S):100美元
- 行权价(K):100美元
- 无风险利率(r):2%(年化)
- 到期时间(t):3个月(即0.25年)
我们需要验证期权价格是否满足无套利条件。假设当前市场价格:
- 看涨期权价格(C):8美元
- 看跌期权价格(P):4.5美元
现在,我们将这些数值代入无套利定价公式来验证:
计算无套利定价公式
首先计算右边的表达式 ( K × e − r t K \times e^{-rt} K×e−rt ):
K × e − r t = 100 × e − 0.02 × 0.25 K \times e^{-rt} = 100 \times e^{-0.02 \times 0.25} K×e−rt=100×e−0.02×0.25
计算 ( e − 0.02 × 0.25 e^{-0.02 \times 0.25} e−0.02×0.25 ):
e − 0.005 ≈ 0.995 e^{-0.005} \approx 0.995 e−0.005≈0.995
因此:
100 × 0.995 = 99.5 100 \times 0.995 = 99.5 100×0.995=99.5
代入公式:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
左边是:
8 - 4.5 = 3.5
右边是:
100 - 99.5 = 0.5
显然,这里不满足无套利条件。
调整后的无套利定价
为了满足无套利条件,我们需要调整看跌期权的价格,使公式成立:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
即:
8 − P = 100 − 99.5 8 - P = 100 - 99.5 8−P=100−99.5
8 − P = 0.5 8 - P = 0.5 8−P=0.5
P = 8 − 0.5 = 7.5 P = 8 - 0.5 = 7.5 P=8−0.5=7.5
所以,在无套利条件下,看跌期权的价格应为7.5美元。
总结
- 看涨期权价格(C):8美元
- 看跌期权价格(P):7.5美元
在这个调整后的例子中:
8 − 7.5 = 100 − 99.5 8 - 7.5 = 100 - 99.5 8−7.5=100−99.5
0.5 = 0.5 0.5 = 0.5 0.5=0.5
这满足了无套利条件。因此,市场在这种情况下没有套利机会,所有期权价格是合理的。
结合前面的无风险套利实例
前面的套利例子中,通过构建保护性看跌和备兑看涨策略,我们发现期权价格存在偏差,导致无风险利润。现在,我们通过无套利条件调整了看跌期权的价格,使其符合市场有效性,从而消除了套利机会。
这个例子说明了在无套利市场中,期权价格如何通过无套利定价公式保持一致,以防止套利机会。
英文版
Example of Arbitrage in the Options Market
To illustrate more clearly, let’s go through a more realistic example of arbitrage.
Example of Arbitrage in the Options Market
Assume the following market prices:
- Underlying stock price: $100
- European call option (strike price $100, 3 months to expiry): $8
- European put option (strike price $100, 3 months to expiry): $5
- Risk-free interest rate: 2% (annualized)
We will use a classic arbitrage strategy known as a “conversion arbitrage.”
Conversion Arbitrage Strategy
Conversion arbitrage involves buying the underlying stock, buying a put option, and selling a call option. If there is a pricing discrepancy between the options and the underlying stock, this strategy can lock in a risk-free profit.
Step-by-Step Process:
-
Buy the underlying stock:
- Purchase 1 share of XYZ company stock at $100.
-
Buy a European put option:
- Purchase a put option with a strike price of $100 for $5.
-
Sell a European call option:
- Sell a call option with a strike price of $100 for $8.
Total Initial Investment:
- Purchase of stock: $100
- Purchase of put option: $5
- Sale of call option: -$8 (you receive $8)
Total initial investment = $100 (stock) + $5 (put option) - $8 (call option) = $97
Payoff at Expiration:
Regardless of the stock price at expiration, your positions are hedged:
-
If the stock price is above $100 (e.g., $110):
- The put option expires worthless.
- The call option is exercised, and you sell the stock at $100.
- You receive $100.
-
If the stock price is below $100 (e.g., $90):
- The put option is exercised, and you sell the stock at $100.
- The call option expires worthless.
- You receive $100.
In both cases, you receive $100 at expiration.
Profit Calculation:
- Total amount received at expiration: $100
- Total initial investment: $97
Profit = $100 - $97 = $3
This $3 risk-free profit is due to the initial mispricing of the options relative to the stock.
Example of No-Arbitrage
In a no-arbitrage market, such discrepancies would not exist. The prices of call and put options would align with the stock price and the risk-free interest rate, preventing such risk-free profits from being made.
Example of No-Arbitrage Pricing in the Options Market
In a no-arbitrage market, option prices should satisfy the following no-arbitrage pricing formula:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
where:
- ( C ) is the price of the call option
- ( P ) is the price of the put option
- ( S ) is the stock price
- ( K ) is the strike price
- ( r ) is the risk-free interest rate
- ( t ) is the time to expiration
Example Illustration
Assume the following market conditions:
- Stock price (S): $100
- Strike price (K): $100
- Risk-free interest rate ( r): 2% (annualized)
- Time to expiration (t): 3 months (or 0.25 years)
We need to verify if the option prices meet the no-arbitrage condition. Assume the current market prices are:
- Call option price ( C): $8
- Put option price ( P): $4.5
Let’s plug these values into the no-arbitrage pricing formula to verify:
Calculating the No-Arbitrage Pricing Formula
First, calculate the right side of the equation ( K × e − r t K \times e^{-rt} K×e−rt ):
K × e − r t = 100 × e − 0.02 × 0.25 K \times e^{-rt} = 100 \times e^{-0.02 \times 0.25} K×e−rt=100×e−0.02×0.25
Calculate ( e − 0.02 × 0.25 e^{-0.02 \times 0.25} e−0.02×0.25 ):
e − 0.005 ≈ 0.995 e^{-0.005} \approx 0.995 e−0.005≈0.995
Thus:
100 × 0.995 = 99.5 100 \times 0.995 = 99.5 100×0.995=99.5
Substitute into the formula:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
Left side:
8 − 4.5 = 3.5 8 - 4.5 = 3.5 8−4.5=3.5
Right side:
100 − 99.5 = 0.5 100 - 99.5 = 0.5 100−99.5=0.5
Clearly, this does not satisfy the no-arbitrage condition.
Adjusted No-Arbitrage Pricing
To satisfy the no-arbitrage condition, we need to adjust the put option price so that the formula holds:
C − P = S − K × e − r t C - P = S - K \times e^{-rt} C−P=S−K×e−rt
So:
8 − P = 100 − 99.5 8 - P = 100 - 99.5 8−P=100−99.5
8 − P = 0.5 8 - P = 0.5 8−P=0.5
P = 8 − 0.5 = 7.5 P = 8 - 0.5 = 7.5 P=8−0.5=7.5
Therefore, under the no-arbitrage condition, the put option price should be $7.5.
Summary
- Call option price ( C): $8
- Put option price ( P): $7.5
In this adjusted example:
8 − 7.5 = 100 − 99.5 8 - 7.5 = 100 - 99.5 8−7.5=100−99.5
0.5 = 0.5 0.5 = 0.5 0.5=0.5
This satisfies the no-arbitrage condition. Thus, the market in this case has no arbitrage opportunities, and all option prices are fair.
Relating to the Previous Risk-Free Arbitrage Example
In the previous arbitrage example, we identified a pricing discrepancy through the protective put and covered call strategy, leading to a risk-free profit. Now, by adjusting the put option price to meet the no-arbitrage condition, we ensure market efficiency and eliminate the arbitrage opportunity.
This example illustrates how option prices, in a no-arbitrage market, are aligned by the no-arbitrage pricing formula to prevent arbitrage opportunities.
后记
2024年6月16日于上海。基于GPT4o模型。
相关文章:
举例以及期权无套利定价公式)
期权无风险套利(Risk-Free Arbitrage)举例以及期权无套利定价公式
期权市场的无风险套利 中文版 期权市场中的套利实例 为了清楚地说明,让我们通过一个现实的例子来展示套利。 期权市场中的套利实例 假设市场上有以下价格: 标的股票价格:100美元欧式看涨期权(行权价100美元,3个月…...
)
Java基础知识巩固自测(上)
前言 该文章适用于已初步了解Java基础知识的入门学习者,便于快速回顾知识点,查漏补缺。 内容包括:Java面向对象相关知识、SQL基础语法 复习建议技巧 实用3W思维法(What、Why、How) 1. What(什么&#x…...
通过 Python+Nacos实现微服务,细解微服务架构
shigen坚持更新文章的博客写手,擅长Java、python、vue、shell等编程语言和各种应用程序、脚本的开发。记录成长,分享认知,留住感动。 个人IP:shigen 背景 一直以来的想法比较多,然后就用Python编写各种代码脚本。很多…...

如何使用new和delete操作符进行动态内存分配和释放?
在C中,new 和 delete 操作符用于在堆(heap)上动态地分配和释放内存。这是管理内存的一种重要方式,特别是在需要创建可变数量或生命周期与程序执行流程不一致的对象时。 使用 new 进行动态内存分配 当你使用 new 操作符时&#x…...

【SCAU数据挖掘】数据挖掘期末总复习题库选择题及解析
1.将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?( C ) A.频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 解析:数据预处理是数据分析和数据挖掘的重要步骤之一,包括数据清洗、集成、变换、规约(如维度规约、数值规约)等。这…...
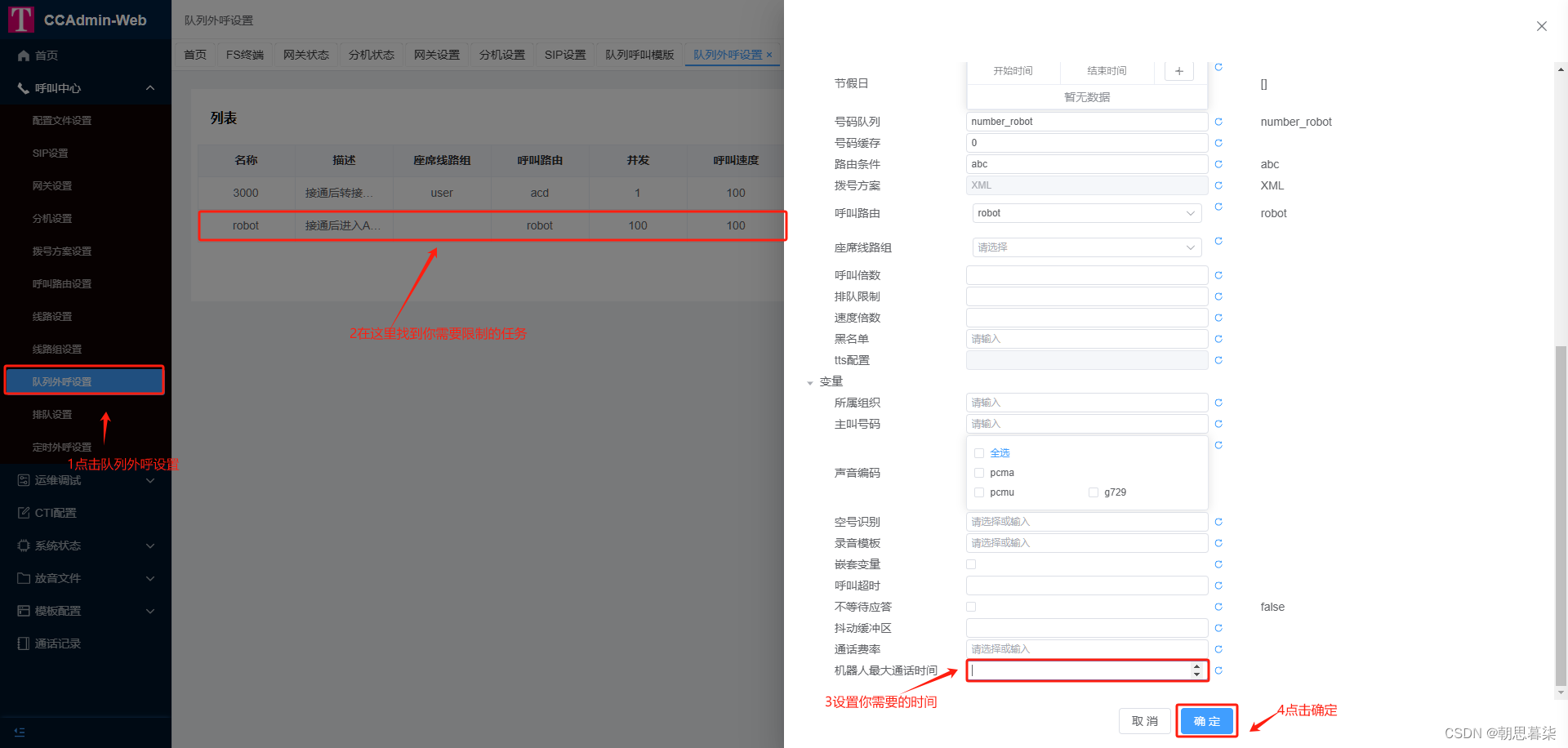
顶顶通呼叫中心中间件-限制最大通话时间(mod_cti基于FreeSWITCH)
顶顶通呼叫中心中间件-限制最大通话时间(mod_cti基于FreeSWITCH) 一、最大通话时间 1、配置拨号方案 1、点击拨号方案 ->2、在框中输入通话最大时长->3、点击添加->4、根据图中配置->5、勾选continue。修改拨号方案需要等待一分钟即可生效 action"sched…...

深度学习:使用argparse 模块
在深度学习中,结合 Bash 脚本和 argparse 模块,可以实现高效的任务自动化和参数管理。Bash 脚本可以用来调度任务和管理环境,而 argparse 模块可以用来解析命令行参数,控制深度学习模型的训练和评估过程。 1.argparse 模块 argp…...

unity text根据文本内容自动设置高度
我们经常会遇到需要根据文字数量动态修改文本框高度的需求,我们可以使用文本的行数*每行的高度来计算文本框的高度,伪代码如下: int oneLineHight 50;// 每行的像素高度 private void ResetTextHight(string str) {//设置文字内容ShowText.…...

ARM 汇编 C语言 for循环
在使用 Keil 编译基于 STM32F103 的 C 语言程序时,生成的汇编代码会有一些不同。STM32F103 是基于 ARM Cortex-M3 内核的微控制器,因为汇编语言是 ARM 汇编,而不是 x86 汇编。 示例 C 代码 假设我们有如下的简单 C 语言 for 循环代码&#x…...
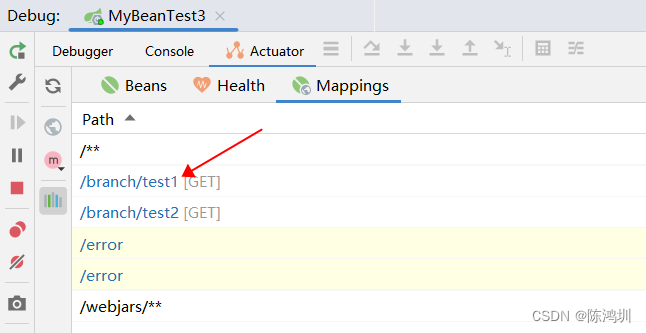
java:【@ComponentScan】和【@SpringBootApplication】扫包范围的冲突
# 代码结构如下: 注意【com.chz.myBean.branch】和【com.chz.myBean.main】这两个包是没有生重叠的。 主程序【MyBeanTest1、MyBeanTest2、MyBeanTest3】这两个类是在包【com.chz.myBean.main】下 # 示例代码 【pom.xml】 <dependency><groupId>org.…...
本学期嵌入式期末考试的综合项目,我是这么出题的
时间过得真快,临近期末,又到了老师出卷的时候。作为《嵌入式开发及应用》这门课的主讲教师,今年给学生出的题目有一点点难度,最后的综合项目要求如下所示,各位学生朋友和教师同行可以评论一下难度如何,单片…...
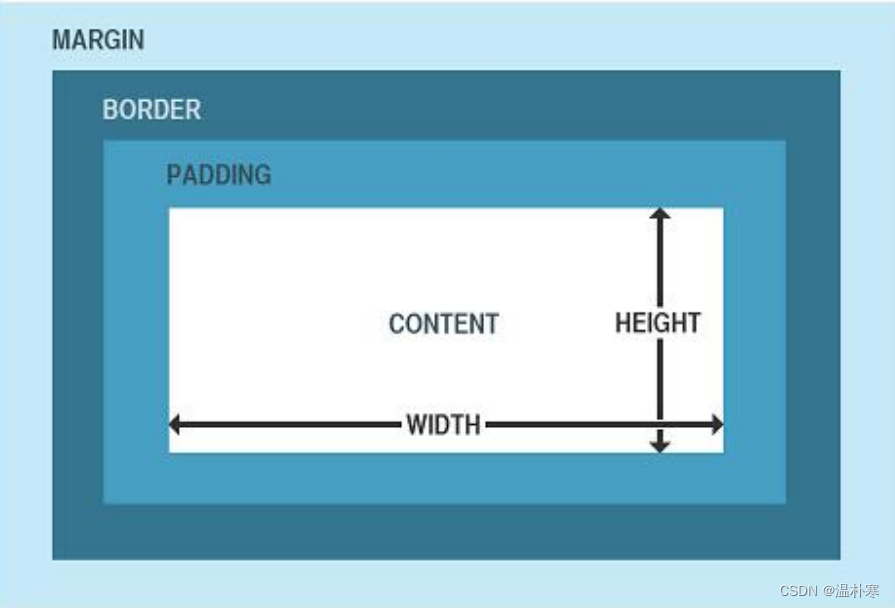
CSS概述
CSS是一种样式表语言,用于为HTML文档控制外观,定义布局。例如, CSS涉及字体、颜色、边距、高度、宽度、背景图像、高级定位等方面 。 ● 可将页面的内容与表现形式分离,页面内容存放在HTML文档中,而用 于定义表现形式…...
Tensorflow-GPU工具包了解和详细安装方法
目录 基础知识信息了解 显卡算力 CUDA兼容 Tensorflow gpu安装 CUDA/cuDNN匹配和下载 查看Conda driver的版本 下载CUDA工具包 查看对应cuDNN版本 下载cuDNN加速库 CUDA/cuDNN安装 CUDA安装方法 cuDNN加速库安装 配置CUDA/cuDNN环境变量 配置环境变量 核验是否安…...
【python】OpenCV GUI——Trackbar(14.2)
学习来自 OpenCV基础(12)OpenCV GUI中的鼠标和滑动条 文章目录 GUI 滑条介绍cv2.createTrackbar 介绍牛刀小试 GUI 滑条介绍 GUI滑动条是一种直观且快速的调节控件,主要用于改变一个数值或相对值。以下是关于GUI滑动条的详细介绍:…...

Qt自定义日志输出
Qt自定义日志输出 简略版: #include <QApplication> #include <QDebug> #include <QDateTime> #include <QFileInfo> // 将日志类型转换为字符串 QString typeToString(QtMsgType type) {switch (type) {case QtDebugMsg: return "D…...
[C++] vector list 等容器的迭代器失效问题
标题:[C] 容器的迭代器失效问题 水墨不写bug 正文开始: 什么是迭代器? 迭代器是STL提供的六大组件之一,它允许我们访问容器(如vector、list、set等)中的元素,同时提供一个遍历容器的方法。然而…...

Java——变量作用域和生命周期
一、作用域 1、作用域简介 在Java中,作用域(Scope)指的是变量、方法和类在代码中的可见性和生命周期。理解作用域有助于编写更清晰、更高效的代码。 2、作用域 块作用域(Block Scope): 块作用域是指在…...
WPF界面设计
1、使用C#-WPF实现抽屉效果-炫酷漂亮的侧边栏导航菜单-SplitViewMD主题重绘原生控件的美观效果-提供源码Demo下载 码源地址:https://download.csdn.net/download/Prince999999/89424685 2、使用C#-WPF实现抽屉效果-菜单导航功能实现,常规的管理系统应该…...

【C#】使用JavaScriptSerializer序列化对象
在C#开发语言编程中,通常使用系统内置的JavaScriptSerializer类来序列化对象,以便将其转换为JSON格式的文本存储与后台服务通信, 在这里将为大家详细介绍一下这个过程。 文章目录 反序列化序列化忽略属性 假设处理的数据中有一个对象类, 如下 public cl…...

HTML静态网页成品作业(HTML+CSS)—— 明星吴磊介绍网页(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有5个页面。 二、作品演示 三、代…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
