c++_0基础_讲解7 练习
这一讲我为大家准备了几道题目,大家试着独自做一下(可能来自不同网站)
整数大小比较 - 洛谷
题目描述
输入两个整数,比较它们的大小。若 x>yx>y ,输出 > ;若 x=yx=y ,输出 = ;若 x<yx<y,输出 < 。
输入格式
一行,包含两个整数 xx 和 yy ,中间用单个空格隔开。 0≤x<232,−231≤y<2310≤x<232,−231≤y<231 。
输出格式
一个字符。若 x>yx>y,输出 > ;若 x=yx=y ,输出 = ;若 x<yx<y ,输出 < ;
输入输出样例
输入 #1复制
1000 100
输出 #1复制
>
首先我们看到数据范围,x 的大小有可能超过 int 的范围,所以我们要使用 long long 来存储。代码如下:#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int main() {long long x, y;cin >> x >> y;if (x > y) {cout <<">";}if (x == y) {cout <<"=";}if (x < y) {cout <<"<";}return 0;
}三角形判断 - 洛谷
题目描述
给定三个正整数,分别表示三条线段的长度,判断这三条线段能否构成一个三角形。
输入格式
输入共一行,包含三个正整数,分别表示三条线段的长度,数与数之间以一个空格分开。(三条边的长度均不超过 1000010000)
输出格式
如果能构成三角形,则输出 1 ,否则输出 0。
输入输出样例
输入 #1复制
1 1 1
输出 #1复制
1
输入 #2复制
1 1 3
输出 #2复制
0
说明/提示
构成三角形的条件:
任意两边长度之和大于第三条边的长度。
根据小学数学的知识可知,任意两边之和大于第三边,即可形成三角形,我们在程序中判断一下即可。
#include<bits/stdc++.h>
using namespace std;
int main() {int a,b,c;cin>>a>>b>>c;int mx=max(a,max(b,c));int sum=a+b+c;sum-=mx;if(sum>mx){cout<<1;}else cout<<0;
}[语言月赛 202405] 最大的和 - 洛谷
题目描述
小 S 喜欢连在一起的数字,如果这些数字的和很大就更好了。
所以她现在要给你一个 n 行 n 列的网格 AA,第 i行第 j列上填有一个整数 Ai,j。
接下来你可以在 A上任取一行、一列或一条与任意对角线平行且只经过网格交叉点的直线(注意,不是线段),满足经过至少一个数字,且经过的数字之和最大。
如果对上面的表述有疑惑,请参考样例解释辅助理解。
你需要告诉小 S 这个最大的数字之和。
输入格式
输入共 n+1 行。
第一行,一个正整数 n,表示方阵的行数、列数。
接下来 n行,每行 n=n 个用空格隔开的整数,其中第 i行第 j个整数表示 Ai,j。
输出格式
输出一行一个整数,表示最大的数字之和。
输入输出样例
输入 #1复制
3 1 1 1 2 2 2 3 3 3
输出 #1复制
9
输入 #2复制
3 -1 1 2 4 0 3 1 9 2
输出 #2复制
13
输入 #3复制
3 -1 -1 -1 -1 -1 -1 -1 -1 -1
输出 #3复制
-1
输入 #4复制
3 -100 -10 -100 -10 99999 -10 -100 -10 -100
输出 #4复制
99979
说明/提示
样例 1 解释
对于样例 11,不难看出第 33 行数字之和最大,有 3+3+3=93+3+3=9。
样例 2 解释
对于样例 22,数字之和最大的,满足条件的线如下所示:
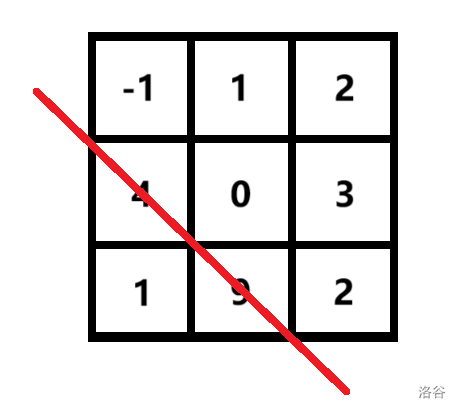
此时有 4+9=134+9=13。
注意,因为要求与对角线平行的直线只能经过网格交点,所以并不能出现同时取 4,1,94,1,9 或同时取 4,1,9,24,1,9,2 这样的情况。
样例 33 解释
取某条只经过一个 −1−1 的直线即为最大。注意,不可以一个数字都不选。
样例 44 解释
显然,取斜着的线一定不优,只能选择中间那一行或一列,答案是 −10+99999−10=99979−10+99999−10=99979。
数据范围
对于前 30%30% 的数据,保证 A1,1A1,1 或 An,nAn,n 的值为网格中唯一的非负整数。
对于另 20%20% 的数据,保证每一行数字相同,且最后一行中的数字之和为最大值。
对于另 20%20% 的数据,保证每一行数字相同,网格中不存在负数。
对于 100%100% 的数据,保证 1≤n≤2×103,−105≤Ai,j≤1051≤n≤2×103,−105≤Ai,j≤105。
题目大意
给定一个 n×nn×n 的方阵,请你取一行,一列,或者与对角线平行的一条只经过格点的直线,满足经过的数字和最大。
题目分析
首先,开一个二维数组 a 来存储方阵上的数字:
int a[2005][2005];
然后开两个变量 ans 和 res。 ans 代表最终答案,初始要赋值成一个很小的负数(比如 −1018−1018);res 代表一个临时变量,用来统计某一行、某一列或某一斜线上的数字和。注意数据范围,要使用 long long 类型:
long long res, ans = -1e18;
接下来考虑求出答案。取一行、一列的情况是好写的。对于取一行的情况,我们可以循环枚举每一行,然后分别算出每一行的数字和,用数字和去更新答案。写法如下:
for(int i = 1; i <= n; i++) {res = 0;for(int j = 1; j <= n; j++)res += a[i][j];ans = max(ans, res);
}
取一列的情况同理,枚举列即可:
for(int i = 1; i <= n; i++) {res = 0;for(int j = 1; j <= n; j++)res += a[j][i];ans = max(ans, res);
}
接下来考虑如何求与对角线平行的情况。这里我们首先需要了解一个知识点:
- 考虑从左上到右下的对角线。对于任意一条与这个对角线平行的直线,其经过的所有格子的行数与列数之差一定相同。
我们这里画图来解释一下。
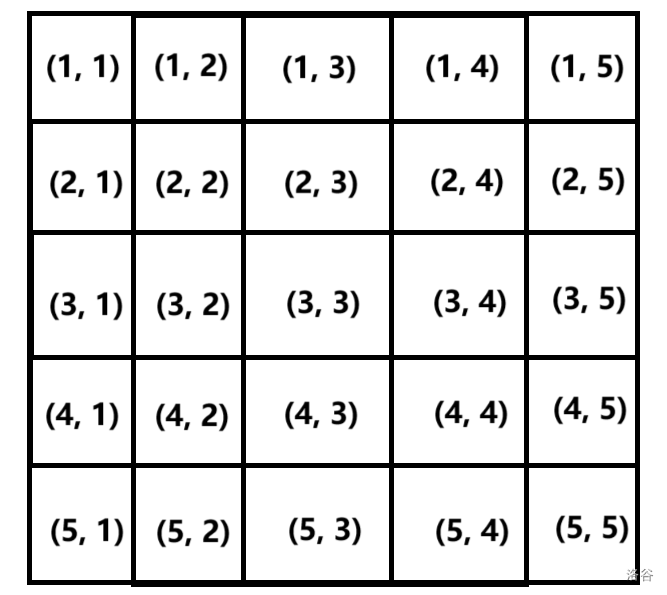
首先,这是一个 5×55×5 的方阵。我们随便取一条从左上到右下的满足条件的斜线:
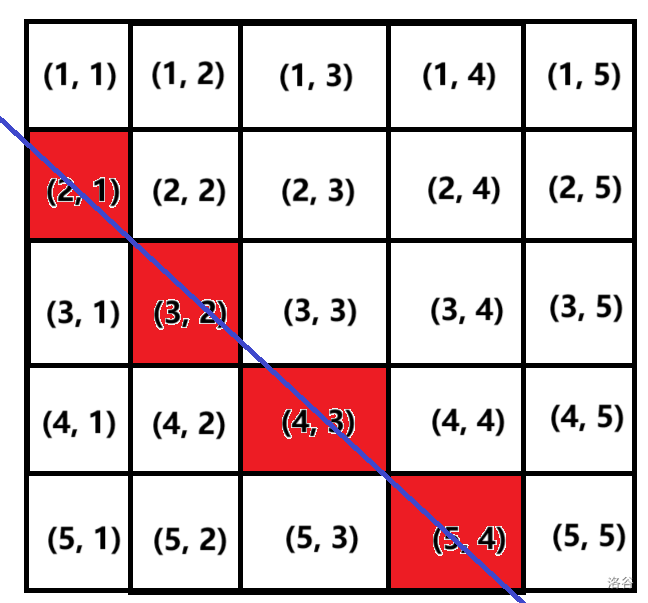
不难发现,(2,1),(3,2),(4,3),(5,4)(2,1),(3,2),(4,3),(5,4) 都满足行数 −− 列数 =1=1。大家也可以试试其它斜线,可以发现都满足上面的规律。
- 考虑从右上到左下的对角线。对于任意一条与这个对角线平行的直线,其经过的所有格子的行数与列数之和一定相同。
我们同样画图来解释一下。
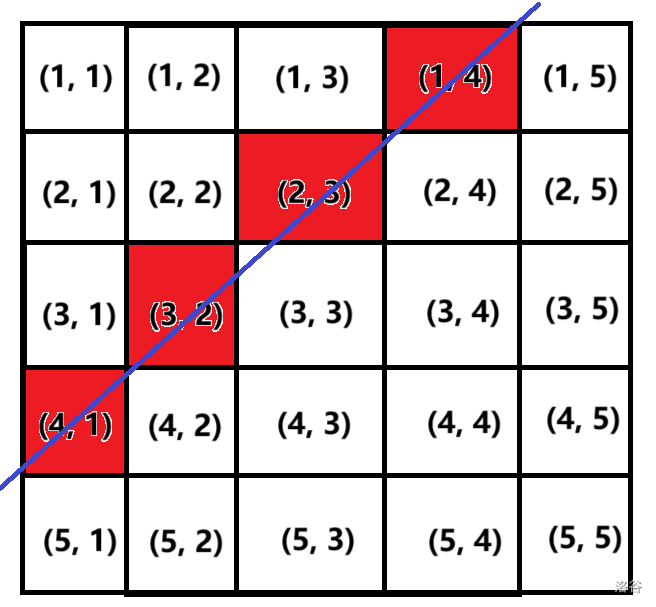
不难发现,(1,4),(2,3),(3,2),(4,1)(1,4),(2,3),(3,2),(4,1) 都满足行数 ++ 列数 =5=5。大家也可以试试其它斜线,可以发现都满足上面的规律。
因此,对于从左上到右下的斜线,我们可以选择枚举行数与列数的差,这样就相当于枚举了这条斜线。然后将斜线上的数字都加起来,去更新答案:
//这里 i 代表正在枚举的行数与列数的差(左上到右下)
//行和列的最小值都是 1,最大值都是 n,所以这个差值最小就是 1-n,最大是 n-1
for(int i = 1-n; i <= n-1; i++) {res = 0;//然后枚举这条线上所有格子的行数 j//那么此时列数就等于 j-ifor(int j = 1; j <= n; j++)//这里 j-i 还要判断范围,是因为要保证这个格子不能出界if(1 <= j-i && j-i <= n) res += a[j][j-i];ans = max(ans, res);
}
从右上到左下的斜线也类似:
//这里 i 代表正在枚举的行数与列数的和(右上到左下)
//行和列的最小值都是 1,最大值都是 n,所以这个和值最小就是 2,最大是 n+n
for(int i = 2; i <= n+n; i++) {res = 0;//然后枚举这条线上所有格子的行数 j//那么此时列数就等于 i-jfor(int j = 1; j <= n; j++)//这里 i-j 还要判断范围,是因为要保证这个格子不能出界if(1 <= i-j && i-j <= n) res += a[j][i-j];ans = max(ans, res);
}
最后输出答案即可:
cout << ans << '\n';相关文章:

c++_0基础_讲解7 练习
这一讲我为大家准备了几道题目,大家试着独自做一下(可能来自不同网站) 整数大小比较 - 洛谷 题目描述 输入两个整数,比较它们的大小。若 x>yx>y ,输出 > ;若 xyxy ,输出 ÿ…...

docker一些常用命令以及镜像构建完后部署到K8s上
docker一些常用命令以及镜像构建完后部署到K8s上 1.创建文件夹2.删除文件3.复制现有文件内容到新建文件4.打开某个文件5.查看文件列表6.解压文件(tar格式)7.解压镜像8.查看镜像9.删除镜像10.查看容器11.删除容器12.停止运行容器13.构建镜像14.启动容器15…...

在typora中利用正则表达式,批量处理图片
一,png格式 在 Typora 中批量将 HTML 图片标签转换为简化的 Markdown 图片链接,且忽略 alt 和 style 属性,可以按照以下步骤操作: 打开 Typora 并加载你的文档。按下 Ctrl H(在 Windows/Linux 上)或 Cmd…...

构建LangChain应用程序的示例代码:33、如何在LangChain框架中使用HumanInputChatModel来模拟人工输入的聊天模型教程
除了HumanInputLLM,LangChain还提供了一个伪聊天模型类,可以用于测试、调试或教育目的。这允许您模拟对聊天模型的调用,并模拟如果人类接收到这些消息会如何响应。 在这篇笔记中,我们将介绍如何使用这个模型。 我们首先在代理中…...

虚拟机使用桥接模式网络配置
1、获取本机的网络详细信息 windowr 输入cmd 使用ipconfig -all 一样即可 在自己的虚拟机中设置网络 虚拟机中的ip ---------192.168.36.*,不要跟自己的本机ip冲突 网关-----------192.168.36.254 一样即可 dns -----------一样即可,我多写了几个&am…...

韩顺平0基础学java——第24天
p484-508 System类 常见方法 System.arrycopy(src,0,dest,1,2); 表示从scr的第0个位置拷贝2个,放到目标数组索引为1的地方。 BigInteger和BigDecimal类 保存大整数和高精度浮点数 BigInte…...

leecode N皇后
深度优先遍历,然后回溯 思考得到的技巧: 1.先思考怎么用学过的数据结构解题 2.回溯不只需要知道最后一步,还需要知道之前所走的每一步 3. 棋盘的生成,.join([]),可以变列表为字符串 看题解得到的技巧: 1.妙啊…...
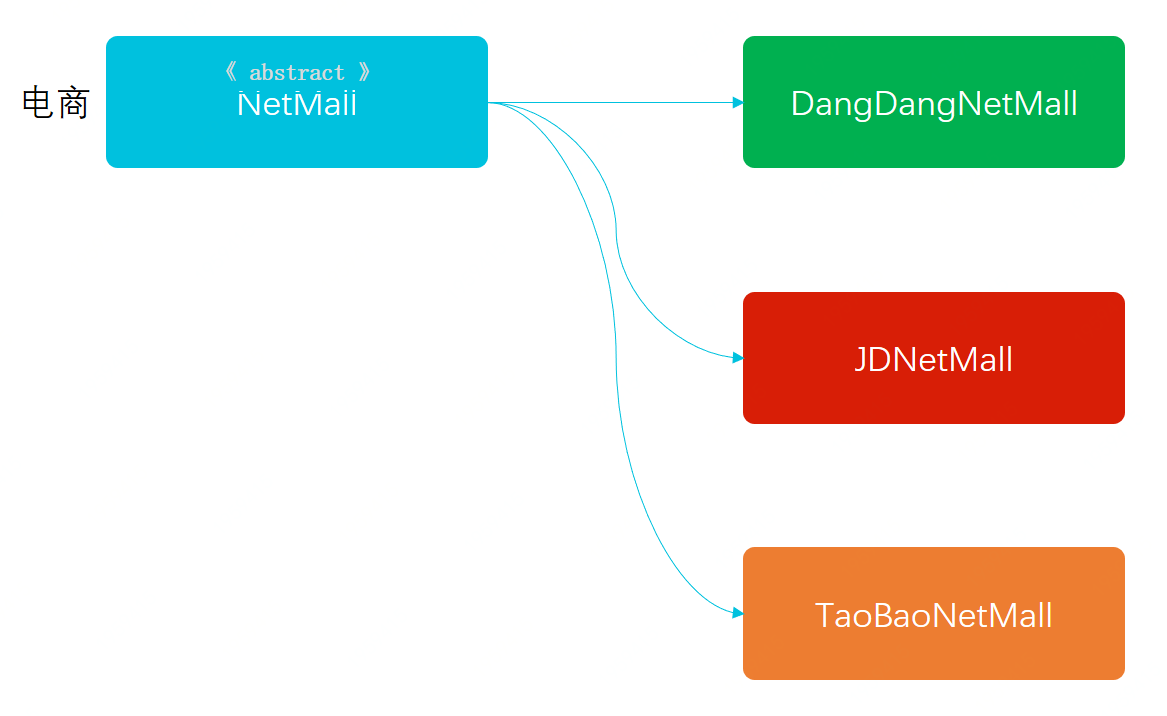
2024050802-重学 Java 设计模式《实战模板模式》
重学 Java 设计模式:实战模版模式「模拟爬虫各类电商商品,生成营销推广海报场景」 一、前言 黎明前的坚守,的住吗? 有人举过这样一个例子,先给你张北大的录取通知书,但要求你每天5点起床,12点…...
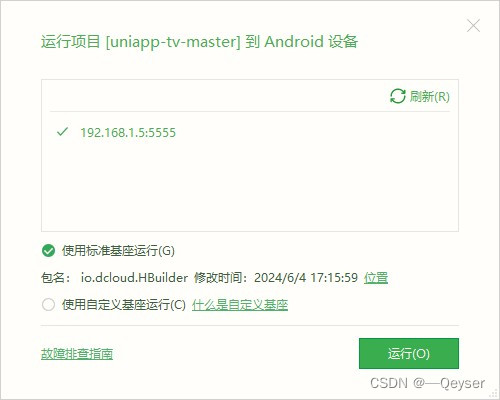
UNIAPP-ADB无线调试
ADB下载 SDK 平台工具版本说明 | Android Studio | Android Developers (google.cn) 环境变量配置 ADB版本查看 adb version 手机使用数据线连接到电脑 手机需要授权adb调试(开发人员选项里面) CMD输入命令 adb tcpip 5555 到了这一步你手机已经启动了adb服务了&…...
【stm32-新建工程】
stm32-新建工程 ■ 下载相关STM32Cube官方固件包(F1,F4,F7,H7)■ 1. ST官方搜索STM32Cube■ 2. 搜索 STM32Cube■ 3. 点击获取软件■ 4. 选择对应的版本下载■ 5. 输入账号信息■ 6. 出现下载弹框,等待下载…...

写点什么吧,作为STM32系列的开篇……
自从本科毕业后,就再也没碰过单片机…… 自从研究生毕业后,就再也没碰过硬件…… 自以为以前单片机玩的熟得很,特别是ATMEGA系列的AVR单片机,由于老师的推荐,本科时花了好多精力在这个系列单片机上面…… 本科时STM…...

代码随想录算法训练营第十天| 232.用栈实现队列|225. 用队列实现栈|20. 有效的括号|1047. 删除字符串中的所有相邻重复项
232.用栈实现队列 文档讲解:代码随想录 视频讲解:栈的基本操作! | LeetCode:232.用栈实现队列_哔哩哔哩_bilibili 知道要用两个栈实现,具体咋做忘了。队列的特性是先进先出,栈是先进后出,入队操…...
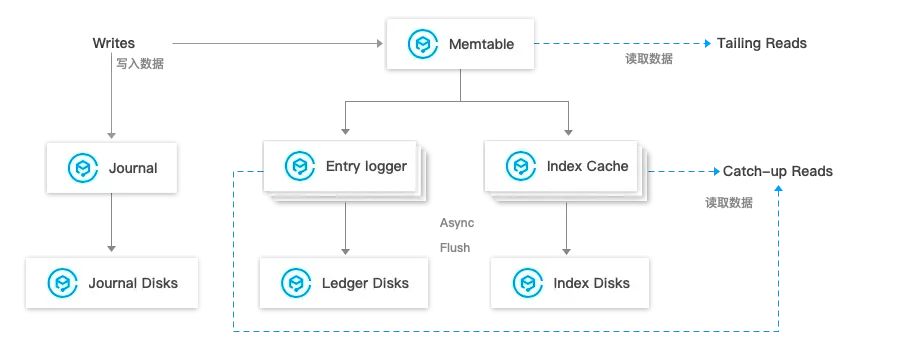
Pulsar 社区周报 | No.2024-06-07 | Apache Pulsar 新分支 3.3 版本发布
“ 各位热爱 Pulsar 的小伙伴们,Pulsar 社区周报更新啦!这里将记录 Pulsar 社区每周的重要更新,每周发布。 ” 本期主题:Apache Pulsar 新分支 3.3 版本发布 Apache Pulsar 新分支 3.3 版本发布:Apache Pulsar 3.3.0[1…...
Go源码--sync库(3):sync.Pool(2)
回收 回收其实就是将 pool.local 置为空 可以让垃圾回收器回收 我们来看下 源码 func init() {// 将 poolCleanup 注册到 gc开始前的准备工作处理器中在 STW时执行runtime_registerPoolCleanup(poolCleanup) }这里注册了清理程序到GC前准备工作 也就是发生GC前需要执行这段代…...
Go如何在本地引用以及发布并引用自定义工具包
如何引用本地自定义工具包 我们首先要准备两个项目,分别为需要引入的工具包和当前项目。 myutils、myproject1. myutils为我们的项目1-工具包 package mypakgeimport "strings"func IsContains(s string) bool {if strings.Contains(s, "a")…...

使用了代理IP怎么还会被封?代理IP到底有没有效果
代理IP作为一种网络工具,被广泛应用于各种场景,例如网络爬虫、海外购物、规避地区限制等。然而,很多用户在使用代理IP的过程中却发现自己的账号被封禁,这让他们不禁产生疑问:使用了代理IP怎么还会被封?代理…...

在WSL2的Ubuntu中安装和使用Docker/Podman
在WSL2的Ubuntu中安装和使用Docker/Podman 0. 目的 当网络环境良好(例如在公司,能直接访问Google等)时, Docker/Podman 安装和使用不是问题。 当网络环境不佳(例如在家里),要把 WSL2 的 Ubun…...

【WEEK16】Learning Objectives and Summaries【Spring Boot】【English Version】
Learning Objectives: Learning SpringBoot Learning Content: Reference video tutorials【狂神说Java】SpringBoot最新教程IDEA版通俗易懂Dubbo and Zookeeper Integration Learning time and outputs: Week16 TUE~FRI 2024.6.11【WEEK16】 【DAY2】Dubbo和Zookeeper集成第…...

AI大模型会让搜索引擎成为历史吗?
AI大模型会让搜索引擎成为历史吗? 随着人工智能技术的不断发展,AI大模型已经在许多领域展现出了强大的能力。从自然语言处理到图像识别,AI大模型的应用越来越广泛。在这种背景下,有人开始提出一个问题:AI大模型是否可…...

SpringSecurity6从入门到实战之SpringSecurity6自定义认证规则
SpringSecurity6从入门到实战之SpringSecurity6自定义认证规则 Spring Security 中默认所有的 http 请求都需要先认证通过后,才能访问。那么, 如何指定不需要认证就可以直接访问的资源呢?比如 用户的登录页面和注册页面,都是不需要…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
