37. CF-Weights Distributing
链接
这是一个比较经典的题目。容易想到求出两段路径重合的部分,然后贪心的放权值。那么跑三次最短路,枚举重合部分的端点即可。
正解没什么好说的。这题有趣的地方在于,如果数据比较弱,可能会把一些错误做法放过去。
一种错误做法是:只求 aaa 点和 ccc 点的单源最短路,然后在枚举端点的时候,认为端点一定在 a,ba,ba,b 或者 b,cb,cb,c 之间的最短路径上。这个结论是错误的,可以构造出这样的反例:
7 8 1 4 6
1 2 3 4 100 100 100 100
1 2
2 3
3 4
3 5
5 6
3 7
1 7
6 7
这里的答案显然是 131313,而错误做法可能会得到 111111111。
这种构造的依据是最短路并不是唯一的。然而,即便最短路是唯一的,上面的做法依然不正确。不妨设 a,ba,ba,b 与 b,cb,cb,c 两条最短路径共用了从点 mmm 到点 bbb 的路径,mmm 到 a,b,ca,b,ca,b,c 三个点的距离分别为 100,10,100100,10,100100,10,100,而在这两条路径外面有一个点 nnn,它到三个点的距离分别为 90,30,9090,30,9090,30,90,那么这个 nnn 点在上面的做法中是不会被遍历到的,但只需设计好权值,就可以使最优解经过这个点。
下面是正解的代码,最短路用 BFS 实现更好。
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
using ll = long long;
const int maxn = 2e5 + 5;
const ll inf = 1e18;
vector<int> g[maxn];
void solve() {int n, m, A, B, C;cin >> n >> m >> A >> B >> C;vector<ll> w(m);for (auto& i : w) cin >> i;for (int i = 1, u, v; i <= m; ++i) {cin >> u >> v;g[u].pb(v);g[v].pb(u);}sort(w.begin(), w.end());vector<int> disA(n + 1, 0x3f3f3f3f);vector<int> disB(n + 1, 0x3f3f3f3f);vector<int> disC(n + 1, 0x3f3f3f3f);vector<int> p(n + 1);function<void(int, vector<int>&)> dijkstra = [&](int s, vector<int>& d) {vector<int> vis(n + 1, 0);struct node {int id, dis;bool operator < (const node& rhs) const {return (dis == rhs.dis ? id > rhs.id : dis > rhs.dis);}};priority_queue<node> q;d[s] = 0;q.push({ s, 0 });while (!q.empty()) {auto [cur, cost] = q.top();q.pop();if (vis[cur]) continue;vis[cur] = 1;d[cur] = cost;for (auto to : g[cur]) {if (vis[to]) continue;if (d[to] > d[cur] + 1) {d[to] = d[cur] + 1;q.push({ to, d[to] });p[to] = cur;}}}};vector<ll> pre(m + 1, 0);for (int i = 1; i <= m; ++i) {pre[i] = pre[i - 1] + w[i - 1];}dijkstra(A, disA);dijkstra(B, disB);dijkstra(C, disC);ll ans = inf;for (int i = 1; i <= n; ++i) {int da = disA[i], db = disB[i], dc = disC[i];if (da + db + dc > m) continue;ans = min(ans, pre[db] + pre[da + db + dc]);}cout << ans << endl;for (int i = 1; i <= n; ++i) {g[i].clear();}
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int T = 1;cin >> T;while (T--) {solve();}return 0;
}
相关文章:

37. CF-Weights Distributing
链接 这是一个比较经典的题目。容易想到求出两段路径重合的部分,然后贪心的放权值。那么跑三次最短路,枚举重合部分的端点即可。 正解没什么好说的。这题有趣的地方在于,如果数据比较弱,可能会把一些错误做法放过去。 一种错误…...

百丽时尚×优维科技×道客战略启动「云原生一体化项目」
3月7日,由百丽时尚集团(以下简称:百丽时尚)联合优维科技、道客共同举办的「云原生一体化项目启动会」在深圳百丽国际大厦圆满落幕,项目合作三方齐聚一堂,就云原生一体化建设战略方案达成合作共识࿰…...
小诺开源技术
小诺开源技术 文章目录小诺开源技术前言页面演示介绍文档学习建议登录地址下载地址前言 近期接触了小诺开源技术的一个前端框架,底层是蚂蚁框架,感觉很好用,不过需要稍微学习并适应一下,推荐给大家,本篇仅用于学习&am…...

AidLux AI应用案例悬赏选题 | 纺织品表面瑕疵检测
AidLux AI 应用案例悬赏征集活动 AidLux AI 应用案例悬赏征集活动是AidLux推出的AI应用案例项目合作模式,悬赏选题将会持续更新。目前上新的选题涉及泛边缘、机器人、工业检测、车载等领域,内容涵盖智慧零售、智慧社区、智慧交通、智慧农业、智能家居等…...
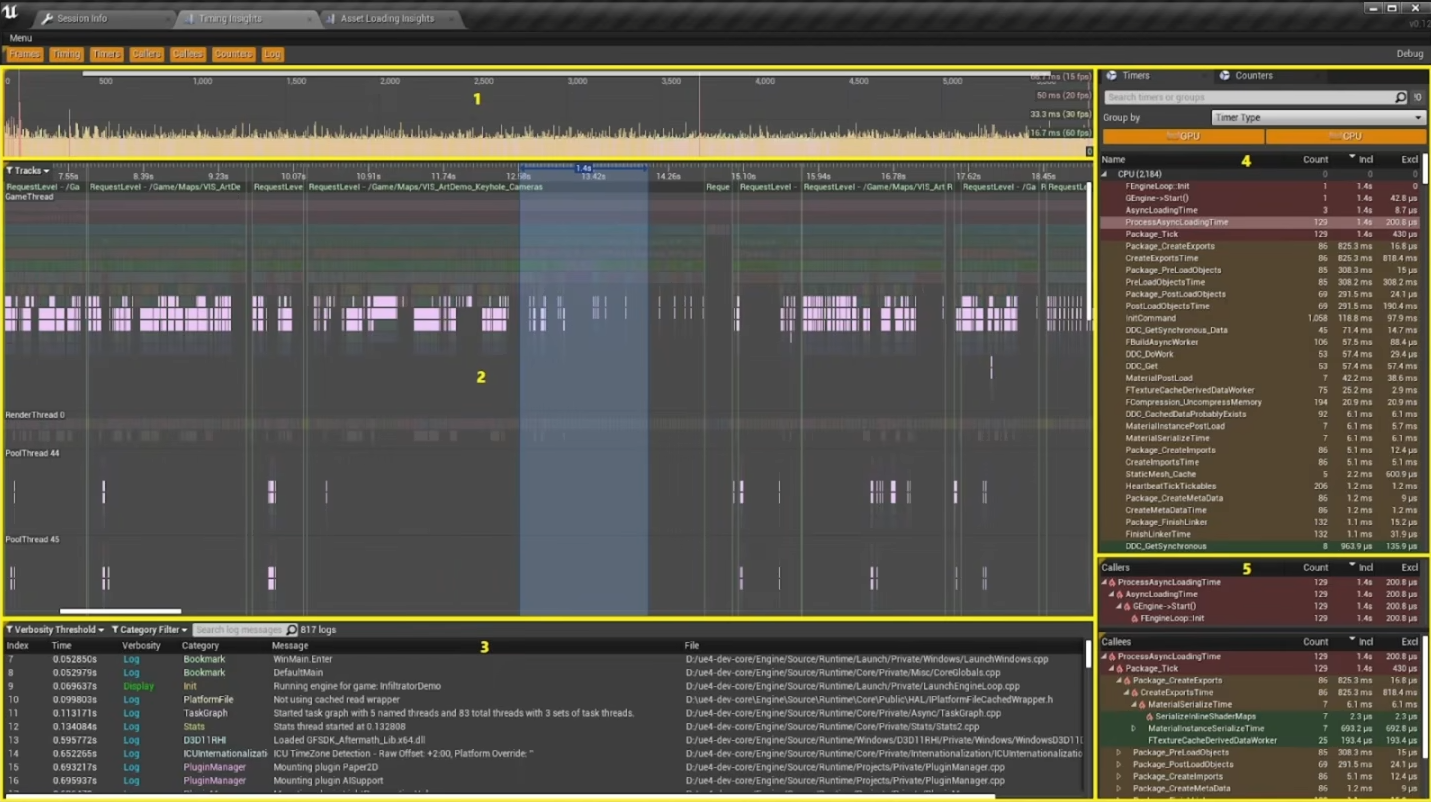
UE官方教程笔记02-实时渲染基础下
对官方教程视频[官方培训]02-实时渲染基础下 | 陈拓 Epic的笔记没听懂的地方就瞎写反射实时渲染中反射是一个非常有挑战的特性UE中有多种不同的方案,各有各的优势和缺点反射捕获屏幕空间反射平面反射LumenRT Reflection反射捕获在指定位置捕获一张Cube Map需要预计算…...

grep命令——在文件中搜索指定的文本模式
grep是英文词组“global search regular expression and print out the line”的缩写,意思是全局搜索正则表达式,并将结果输出。 通常将grep命令与正则表达式搭配使用,命令选项作为搜索过程中的补充或对输出结果的筛选,命令模式十…...
:90子集II、491递增子序列、46全排列)
数据结构刷题(二十二):90子集II、491递增子序列、46全排列
1.子集II题目链接思路:这是一道标准的组合问题数组排序去重。依然是使用回溯。注意:去重代码只需要判断同一树层上是否有重复,同组合总和II(https://blog.csdn.net/xiaomingming99/article/details/129396344)解法&…...
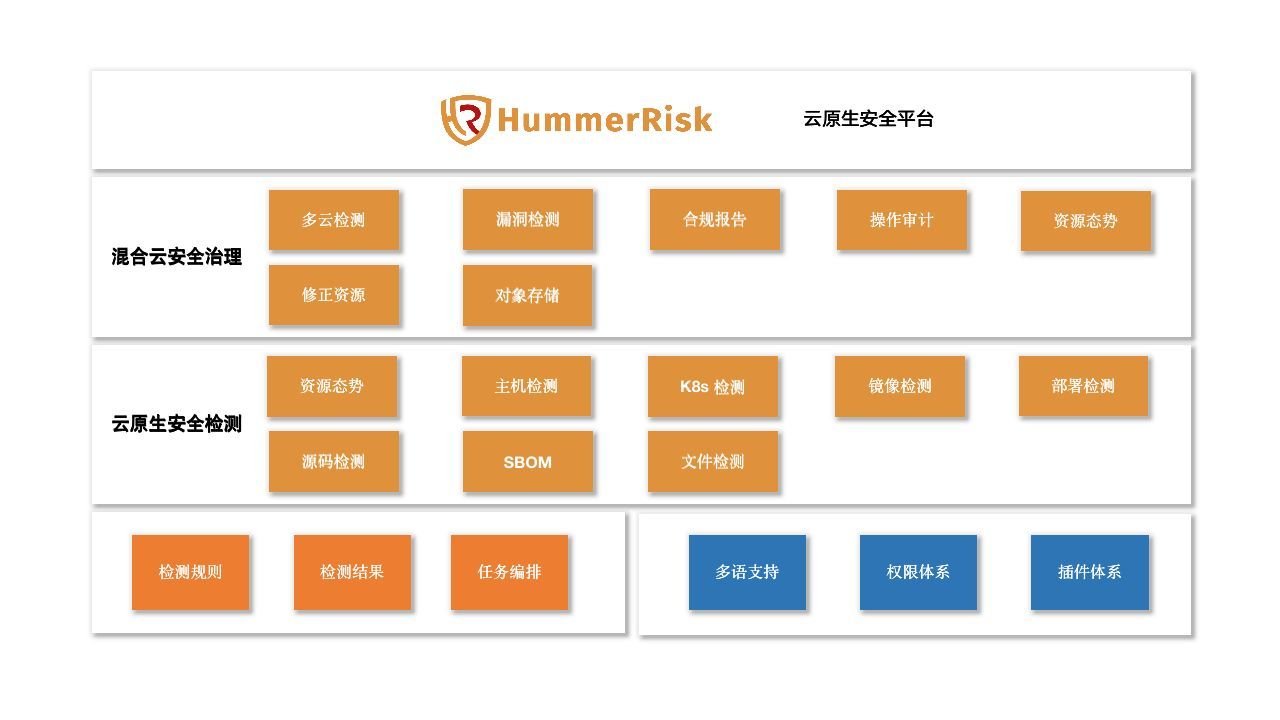
AI+人类,实现高效网络安全
导语 聊天机器人和生成式人工智能(如 ChatGPT)突然成为主流让很多人感到担忧。很多人开始担忧,人工智能取代人的时代已经到来。 幸运的是,事实并非如此。 更有可能的情况是,人类将与 AI 合作创建工作角色的混合模型。…...

牛客小白月赛68【A-E】
文章目录A.Tokitsukaze and New Operation【模拟】B.Tokitsukaze and Order Food Delivery【模拟、特判】C.Tokitsukaze and Average of Substring【暴力、前缀】D.Tokitsukaze and Development Task【记忆化搜索】E.Tokitsukaze and Colorful Chessboard【预处理,二…...

WIFI P2P架构
WI-FI P2P定义架构3个组件组织结构技术标准P2P DiscoveryDevice Discovery(扫描)流程p2p probe 管理帧Group Formation(组网)GO Negotiation(GON)流程P2P Public Action管理帧Provision Discoveryÿ…...

架构师之中台思维_系统发展之路_结果和抽象之间平衡的艺术
父文章 如何成为一名架构师,架构师成长之路_golang架构师成长之路_个人渣记录仅为自己搜索用的博客-CSDN博客 任何系统的发展都是如此. 1. 业务增长 2. 烟囱增长 _ 结果优先 _ 太快去抽象抽象不好 3. 太多的烟囱, 3.1 抽象复用为平台 3.2 面对更多新的业务,提供不同的枚举值…...

23届非科班选手秋招转码指南
1.秋招情况介绍 1.1自我介绍 我是一名23届非科班转码选手,本硕均就读于某211院校机械专业,秋招共计拿下12份offer,包括大疆创新、海康威视、联发科技、理想汽车、中电28、阳光电源等各行业、各种性质企业的意向。主要的投递岗位为嵌入式软件…...

《传感器技术》考试学习笔记
文章目录一、选择题二、简答题1.什么是传感器?传感器的共性是哪些?2.差动变气隙式传感器电感传感器的灵敏度推导过程是什么(推导公式)?与单极性进行比较它们的优缺点是哪些?3.霍尔传感器如何进行微位移测量…...
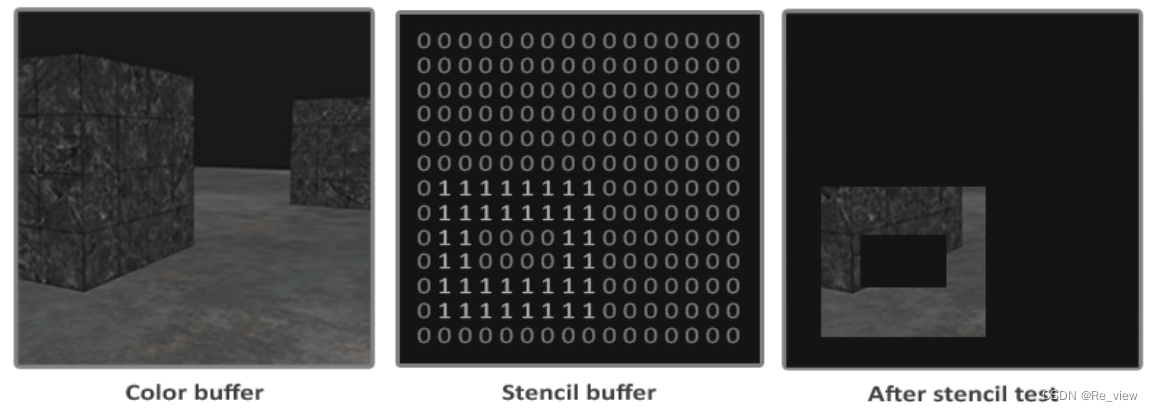
第十五章 opengl之高级OpenGL(模板测试)
OpenGL模板测试模板函数物体轮廓模板测试 当片段着色器处理完一个片段后,模板测试就会开始执行。类似于深度测试,模板测试也可能会丢弃片段。被保留的片段会进入深度测试,可能会丢弃更多的片段。 模板测试是根据模板缓冲来进行的。一个模板缓…...
【C语言蓝桥杯每日一题】—— 单词分析
【C语言蓝桥杯每日一题】—— 单词分析😎前言🙌单词分析🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者…...

Web2:Tomcat
二.Web2:Tomcat 1.Tomcat的配置 2.Tomcat的工作方式 3.Tomcat服务器的虚拟映射 4.Tomcat部署到IDEA中使用 二.Web2:Tomcat 1.Tomcat的配置 ①安装下载Tomcat 配置好JAVA_HOME启动时保证端口号8080不被占用 ②下载后的目录结构 bin 启动或关闭to…...

C++语法规则2(C++面向对象)
继承 面向对象程序设计中最重要的一个概念是继承。继承允许我们依据另一个类来定义一个类,这使得创建和维护一个应用程序变得更容易。这样做,也达到了重用代码功能和提高执行效率的效果。 当创建一个类时,您不需要重新编写新的数据成员和成…...
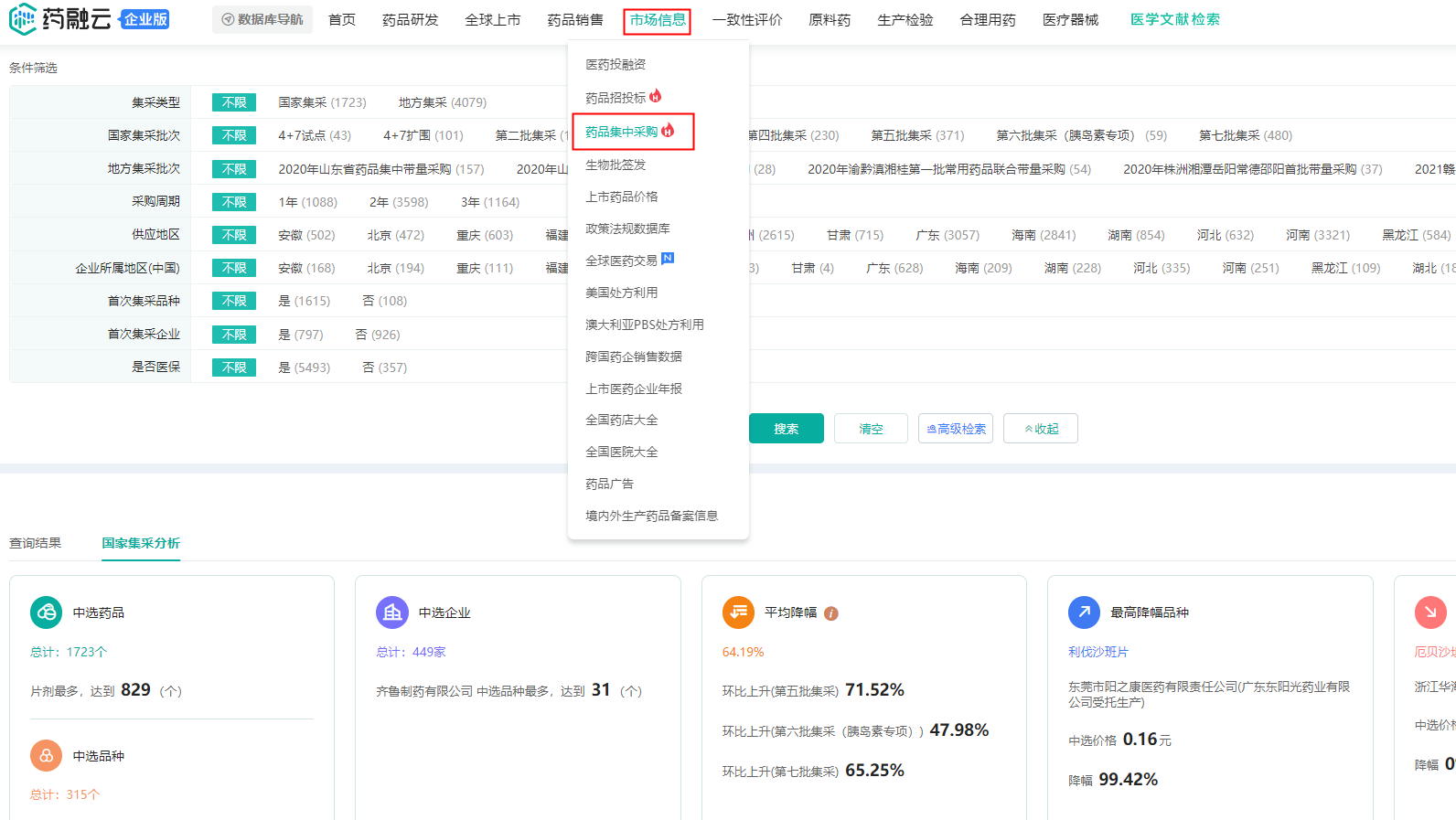
第八批国家药品集中采购-(附药品集采目录明细下载)
2023年3月2日,‘国家组织药品联合采购办公室’发出了《全国药品集中采购文件》,宣告了第八批国家组织药品集中采购工作正式开展,其公告中还包含三个附表分别为‘采购品种目录’、‘各地区首年约定采购量’、‘各采购品种首年约定采购量’&…...
政府工作报告连提9年科技创新 企业研发如何“又快又好”
今年的政府工作报告, “科技创新” 这一描述连续出现7次,这也是自2015年开始, “科技创新” 这一概念在全国“两会”政府工作报告中连续九年被提到。政府工作报告指出,科技政策要聚焦自立自强,完善新型举国体制&#x…...
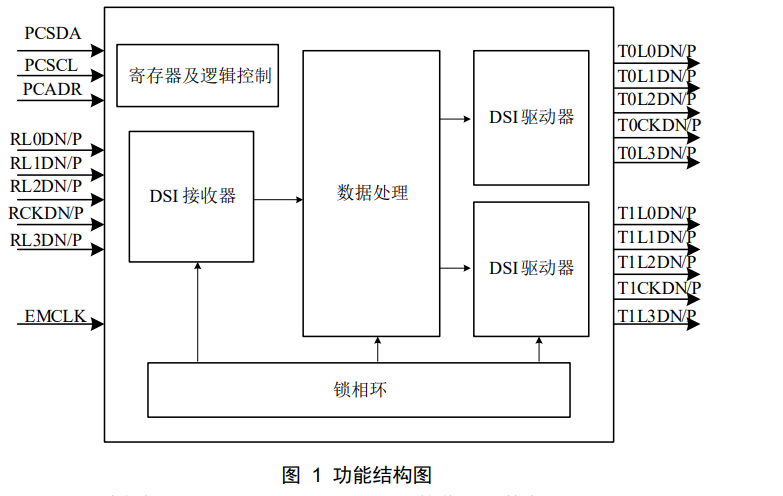
GM8773C 是一款 1:2 DSI 桥接芯片,可实现 4 路进 8 路出转换器功能、视频分离器功能。
GM8773C 是一款 1:2 DSI 桥接芯片,可实现 4 路进 8 路出转换器功能、视频分离器功能。芯片内集成了一个 4 路单一链路的 MIPI DSI 接收器和 8 路双链路 MIPI DSI 发送器。 接 收 器 每 路 可 以 支 持 到 2.0Gbps/lane , 可 以 最 高 支 持 到…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
