【LeetCode 动态规划】买卖股票的最佳时机问题合集
文章目录
- 1. 买卖股票的最佳时机含冷冻期
1. 买卖股票的最佳时机含冷冻期
题目链接🔗

- 🍎题目思路:


- 🍎题目代码:
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n + 1, vector(3, 0));dp[0][0] = 0, dp[0][1] = -prices[0], dp[0][2] = 0;for (int i = 1; i < n; i ++){// 第 i 天结束后处于冷冻期dp[i][0] = dp[i - 1][1] + prices[i];// 处于 买入dp[i][1] = max(dp[i - 1][2] - prices[i], dp[i - 1][1]);// 处于 可交易dp[i][2] = max(dp[i - 1][0], dp[i - 1][2]);}return max(dp[n - 1][0], dp[n - 1][2]);}
};

相关文章:

【LeetCode 动态规划】买卖股票的最佳时机问题合集
文章目录 1. 买卖股票的最佳时机含冷冻期 1. 买卖股票的最佳时机含冷冻期 题目链接🔗 🍎题目思路: 🍎题目代码: class Solution { public:int maxProfit(vector<int>& prices) {int n prices.size();ve…...
)
python学习:语法(2)
目录 对象的布尔值 分支结构 双分支结构 多分支结构 嵌套if的使用 条件表达式 Pass语句 range()函数的使用 流程控制语句 对象的布尔值 Python一切皆对象,所有对象都有一个布尔值,通过内置函数bool()获取对象的布尔值 这些…...
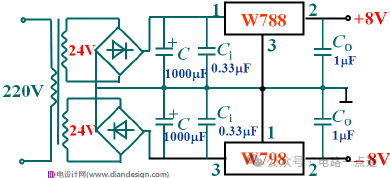
经典电源电路基础(变压-整流-滤波-稳压)
1.电源电路的功能和组成 电子电路中的电源一般是低压直流电,先把220v交流电变换成低压直流电,再用整流电路变成脉动的直流电,最后用滤波电路滤除掉脉动直流中的交流成分后才能得到直流电。有的电子设备对电源的质量要求很高,所以…...
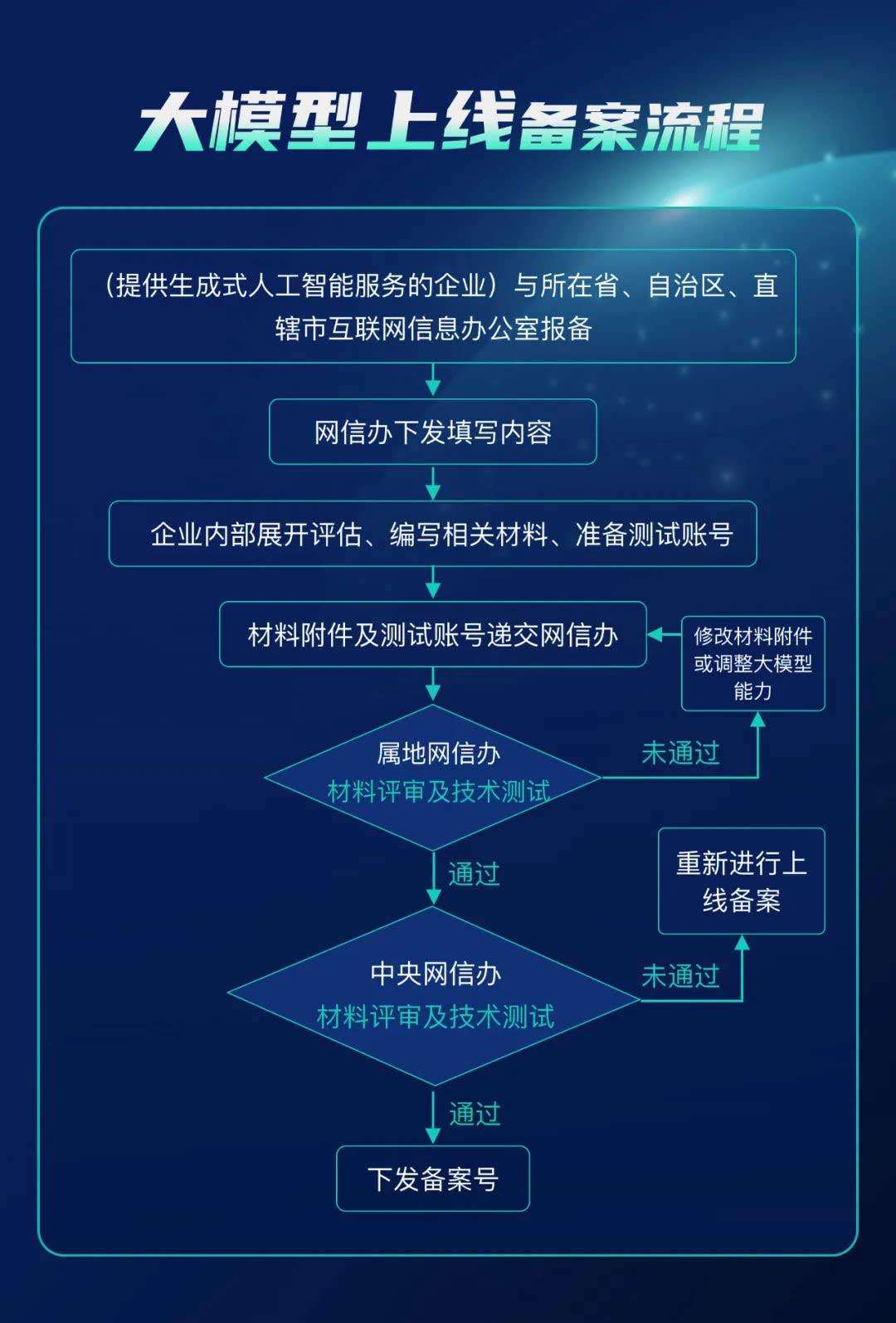
生成式人工智能备案办理指南,深度解析大模型备案全流程
早在2023年年初,国家互联网信息办公室、工业和信息化部、公安部针对深度合成服务制定的《互联网信息服务深度合成管理规定》(“《深度合成管理规定》”)顺利施行,其明确了深度合成服务相关方的义务与主体责任,强化了对…...

1527. 患某种疾病的患者
1527. 患某种疾病的患者 题目链接:1527. 患某种疾病的患者 代码如下: # Write your MySQL query statement below select patient_id,patient_name,conditions from Patients where conditions like "DIAB1%" or conditions like "% DI…...
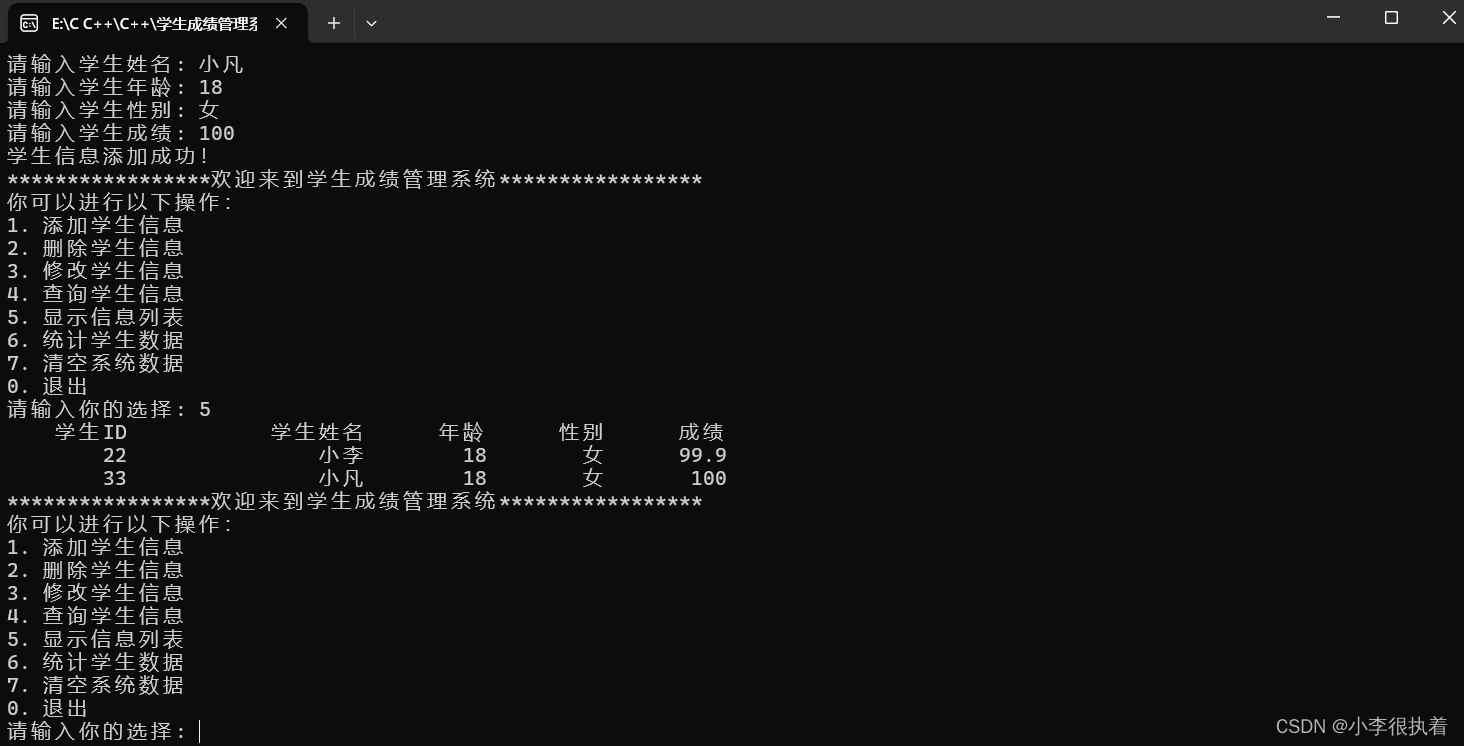
【C/C++】【学生成绩管理系统】深度剖析
可接各类C/C管理系统课设 目录 实现功能 部分1:系统设置和主菜单 1. 引入头文件 2. 定义结构体 3. 函数声明 4. 主函数 部分2:添加学生信息 部分3:删除学生信息 部分4:修改学生信息 部分5:查询学生信息 部分…...

C++作业第四天
#include <iostream> using namespace std; class Per { private: string name; int age; int *high; double *weight; public: //构造函数 Per() { cout << "Per的无参构造" << endl; } Per(str…...

设计模式之工厂方法模式(Factory Method Pattern)
目录 1.1、前言1.2、工厂方法模式简介1.2.1、工厂方法模式的主要特点1.2.2、工厂方法模式的主要结构1.2.3、使用工厂方法模式的好处 1.3、SpringBoot中那些场景使用了工厂方法模式1.4、日常工作中那些业务场景可以使用工厂方法模式1.5、工厂方法模式实战(以某商场一…...

API接口设计的18条规范
API接口设计的18条规范 签名 目的:防止数据被篡改 实现方法: 接口请求方将请求参数、时间戳和密钥拼接成一个字符串使用MD5等hash算法生成签名sign在请求参数或请求头中增加sign参数,传递给API接口API接口网关服务验证传递的sign值&#…...

adb简单使用命令
1. 查看当前连接的设备 adb devices 2. 文件路径 adb install apk 注意文件路径中不能有中文 3. adb shell ps Toplogcatlogcat可以结合greplogcat *:w 显示警告级别以上de 4. adb uninstall 软件名 1.软件名如何查看? 使用命令adb shell pm list packages会…...

构建 deno/fresh 的 docker 镜像
众所周知, 最近 docker 镜像的使用又出现了新的困难. 但是不怕, 窝们可以使用曲线救国的方法: 自己制作容器镜像 ! 下面以 deno/fresh 举栗, 部署一个简单的应用. 目录 1 创建 deno/fresh 项目2 构建 docker 镜像3 部署和测试4 总结与展望 1 创建 deno/fresh 项目 执行命令…...

数据库 | 数据库设计的步骤
1.需求分析 调查机构情况与熟悉业务活动,明确用户的需求,确定系统的边界,生成数据字典和用户需求规格说明书 2.概念结构设计 将从需求分析中得到的用户需求抽象为概念模型,设计E-R模型 3.逻辑结构设计 将E-R图转换为和DBMS相…...

改进YOLO系列 | CVPR 2021 | Involution:超越convolution和self-attention的神经网络算子
Involution:超越卷积和自注意力的新型神经网络算子(中文综述) 简介 Involuton是CVPR 2021上提出的新型神经网络算子,旨在超越卷积和自注意力,提供更高效、更具表达力的特征提取能力。 Involution原理 Involution的…...

落地速度与效果之争,通用VS垂直,我的观点和预测。
标题:AI大模型战场:通用VS垂直,谁将领跑落地新纪元? 摘要:随着人工智能技术的飞速发展,大模型的应用场景日益广泛。在这场竞赛中,通用大模型和垂直大模型各有优势,落地速度和可能性也…...

【Android面试八股文】在Android中,出现ClassNotFound的有可能的原因是什么?
在Android环境下类未找到的可能原因 在Android环境下,类未找到的可能原因包括但不限于以下几点: 类路径问题:Android应用使用的类通常存储在APK文件中。如果类所在的APK文件没有被正确加载,或者应用的类路径配置有误,就会导致类未找到的错误。 多DEX文件加载问题:在一些…...

模板引擎与 XSS 防御
在 View 层,可以解决 XSS 问题。在本书的“跨站脚本攻击”一章中,阐述了“输入检查” 与“输出编码”这两种方法在 XSS 防御效果上的差异。XSS 攻击是在用户的浏览器上执行的, 其形成过程则是在服务器端页面渲染时,注入了恶意的 H…...

vue3轮播图怎么做
先看效果 实现代码 <n-carouseleffect"card"dot-type"line"draggable:autoplay"!isHovered":current-index"currentIndex"prev-slide-style"transform: translateX(-150%) translateZ(-450px);opacity:1"next-slide-st…...
ubuntu中安装docker并换源
使用 Ubuntu 的仓库安装 Docker sudo apt update现在,你可以使用以下命令在 Ubuntu 中安装 Docker 以及 Docker Compose: sudo apt install docker.io docker-composeDocker 包被命名为 docker.io,因为在 Docker 出现之前就已经存在一个名为…...

HTML静态网页成品作业(HTML+CSS)—— 环保主题介绍网页(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有5个页面。 二、作品演示 三、代…...

深入了解RSA加密算法
目录 前言 一、什么是RSA? 二、RSA加密的基本概念 1.非对称加密 2.密钥生成 3.加密和解密 三、RSA加密的工作原理 四、RSA的应用场景 五、RSA加密解密的实现 六、RSA算法的局限性及改进措施 前言 在当今的数字化时代,信息的安全性成为了人们关注…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
