代码随想录算法训练营Day41|背包问题、分割等和子集
背包问题
二维
46. 携带研究材料(第六期模拟笔试) (kamacoder.com)
dp数组有两维,横轴表示背包重量j(0-j),纵轴表示不同物品(0-i),dp[i][j]即表示从下标为[0-i]的物品里任意取,对于重量为j的背包,最大的价值是多少。dp[i][j]的对物品i来说只有2种情况,物品i未放入或者放入,如果物品i未放入,由dp[i-1][j]可以推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i-1][j](当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)(参考代码随想录 (programmercarl.com))放物品时,
dp[i][j] =dp[i-1][j-weight[i]]+value[i],即当未放入i时,且重量为j-weight[i]的dp值加上i的价值。
即dp[i][j]的最终推导公式为:dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
考虑到dp[i][j]的含义,则dp[i][0]意味着背包重量为0的价值,理应全为0,dp[i][0]的值初始化全部为0,此外当i为0时,若j<weight[0]时,dp[i][j]的值应该为0,因为背包容量比编号为0的物品重量要小,而当j>=weight[0]时,dp[0][j]的值应该是value[0],因为背包容量足够放编号为0的物品(注意这里是0-1背包问题,只有放入和取出两种操作,所以这里dp[0][j]只为values[0]而不是values[0]的倍数)
由于dp的递推公式dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]),当前dp[i][j]仅与之前的元素有关,其他地方无需初始化。
vector<vector<int>>dp(weight.size(),vector<int>(bagweight + 1, 0));
for(int j = weight[0]; j <= bagweight; j++){dp[0][j] = value[0];
}之后是确定遍历顺序,对物品和背包的遍历都是可行的。
以遍历物品为例,当j<weight[i]时,无法将物品i放入,则dp[i][j] = dp[i-1][j],否则为上述的dp公式。
for(int i = 1; i < weight.size();i++){for(int j = 0; j <= bagweight; j ++){if(j < weight[i])dp[i][j] = dp[i-1][j];elsedp[i][j] = max(dp[i][j-1],dp[i-1][j-weight[i]]+value[i]);}
}遍历背包的话
for(int j = 0; j <= bagweight; j++){for(int i = 0; i < weight.size(); i++){if(j < weight[i])dp[i][j] = dp[i-1][j];elsedp[i][j] = max(dp[i-1][j],dp[i-1][j-value[i]] + value[i]);}
}只是变更一下顺序,其他一样(对本题是这样的)。
之后就是返回dp数组的最大值即可。
代码随想录的代码如下:
//二维dp数组实现
#include <bits/stdc++.h>
using namespace std;int n, bagweight;// bagweight代表行李箱空间
void solve() {vector<int> weight(n, 0); // 存储每件物品所占空间vector<int> value(n, 0); // 存储每件物品价值for(int i = 0; i < n; ++i) {cin >> weight[i];}for(int j = 0; j < n; ++j) {cin >> value[j];}// dp数组, dp[i][j]代表行李箱空间为j的情况下,从下标为[0, i]的物品里面任意取,能达到的最大价值vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化, 因为需要用到dp[i - 1]的值// j < weight[0]已在上方被初始化为0// j >= weight[0]的值就初始化为value[0]for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}for(int i = 1; i < weight.size(); i++) { // 遍历科研物品for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量// 如果装不下这个物品,那么就继承dp[i - 1][j]的值if (j < weight[i]) dp[i][j] = dp[i - 1][j];// 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值// 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}int main() {while(cin >> n >> bagweight) {solve();}return 0;算法使用两层嵌套循环来补全dp数组,外层执行weight.size()次,即n次,内层执行了bagweight+1次,定为m次,时间复杂度为O(n*m),空间复杂度使用了二维数组,O(n*m)。
一维
滚动数组,不太理解,周末看看。
代码随想录 (programmercarl.com)
// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;int main() {// 读取 M 和 Nint M, N;cin >> M >> N;vector<int> costs(M);vector<int> values(M);for (int i = 0; i < M; i++) {cin >> costs[i];}for (int j = 0; j < M; j++) {cin >> values[j];}// 创建一个动态规划数组dp,初始值为0vector<int> dp(N + 1, 0);// 外层循环遍历每个类型的研究材料for (int i = 0; i < M; ++i) {// 内层循环从 N 空间逐渐减少到当前研究材料所占空间for (int j = N; j >= costs[i]; --j) {// 考虑当前研究材料选择和不选择的情况,选择最大值dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);}}// 输出dp[N],即在给定 N 行李空间可以携带的研究材料最大价值cout << dp[N] << endl;return 0;
}分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
本来想着直接排序然后依次加入最小的数,然后发现果然有错[1,1,2,2]。
以[1,5,11,5]这个题例为例,可以抽象为 一个背包容量为11,剩余元素(只能使用1次)是否能装满这个容量为11的背包。0-1背包问题。
DP数组含义,容量为j的最大价值为dp[j],当dp[target] == target时,表示能装满(此处的target为数组sum的一半,因为两个子集和要相等),即能实现分割等和子集。
背包容量从0到10001,因为数字总和不超过20000,则target<=10000,dp数组长度到达10001就够了。
dp[j] = max(dp[j],dp[j - nums[i]]+ nums[i]);
对dp的初始化,由于nums数组全为正整数,可以全部初始化为0,(若存在负数,则应初始化为INT_MIN)。
遍历顺序物品遍历在外,背包遍历在内层,且内层倒序遍历。参考代码随想录 (programmercarl.com)
最后需考虑,当dp[target] == target时,返回true,否则为false。
此外,若sum%2 == 1,则表明sum为奇数,不存在两个相等的子数组和,return false。剪枝。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0; for(auto x:nums){sum += x; // 计算数组元素的总和}// 如果总和是奇数,那么不能平分,直接返回falseif(sum%2 == 1)return false;// 计算目标和,即每个子集应该达到的和const int target = sum/2;// 初始化动态规划数组dp,大小为10001,初值都为0// dp[j]表示是否能够从前i个数字中选取一些数字,使得这些数字的和为jvector<int>dp(10001, 0);// 遍历数组中的每个数字for(int i = 0; i < nums.size();i++){// 从大到小遍历目标和及其以下的值for(int j = target; j >= nums[i]; j--){// 更新dp[j],选取或不选取当前数字,取两种情况的最大值dp[j] = max(dp[j],dp[j - nums[i]] +nums[i]);}}// 如果dp[target]等于target,说明可以找到和为target的子集,返回trueif(dp[target] == target)return true;return false;}
};
算法的时间复杂度为O(n^2),空间复杂度为O(n)。
相关文章:

代码随想录算法训练营Day41|背包问题、分割等和子集
背包问题 二维 46. 携带研究材料(第六期模拟笔试) (kamacoder.com) dp数组有两维,横轴表示背包重量j(0-j),纵轴表示不同物品(0-i),dp[i][j]即表示从下标为[0-i]的物品…...

oracle SCHEDULER
从Oracle 10g开始,推荐使用DBMS_SCHEDULER包,因为它提供了更强大的功能和灵活性,包括更复杂的调度规则、依赖管理和事件驱动等 1. 用法 DBMS_SCHEDULER.CREATE_JOB (job_name IN VARCHAR2,job_type IN VARCHAR2,job_action IN VARCHAR2,…...

实现虚拟机的难点
一、背景 目前的虚拟机有很多,例如VMWare、VitrualBox、QEMU、JVM、Python虚拟机等等。 二、虚拟机的作用 在一台已有的计算机中,忽略实际操作系统种类和硬件的型号,用一些接口库来搭建一台用户想要的,虚拟的程序运行环境。 例如…...
JAVA-线程
先上图,有点长,比较碎,有xmind文件......,详细内容均在图片里介绍了,提供了PDF文件 1.线程简介 进程是操作系统中正在执行的不同的应用程序,例如:我们可以同时打开Word和记事本 线程是一个应用…...

代码随想录——电话号码的字母组合(Leetcode17)
题目链接 回溯 class Solution {List<String> res new ArrayList<String>();StringBuilder str new StringBuilder();HashMap<String, String> Sites new HashMap<String, String>();public List<String> letterCombinations(String digit…...

多款可观测产品全面升级丨阿里云云原生 5 月产品月报
云原生月度动态 云原生是企业数字创新的最短路径。 《阿里云云原生每月动态》,从趋势热点、产品新功能、服务客户、开源与开发者动态等方面,为企业提供数字化的路径与指南。 趋势热点 🥇 阿里云云原生产品负责人李国强:推进可…...

python实践笔记(三): 异常处理和文件操作
1. 写在前面 最近在重构之前的后端代码,借着这个机会又重新补充了关于python的一些知识, 学习到了一些高效编写代码的方法和心得,比如构建大项目来讲,要明确捕捉异常机制的重要性, 学会使用try...except..finally&…...

Excel VLOOKUP 使用记录
Excel VLOOKUP 使用记录 VLOOKUP简单使用 VLOOKUP(lookup_value,table_array,col_index_num,[range-lookup]) 下面是excel对VLOOKUP 的解释 lookup_value(查找值):要匹配查找的值 table_array(数据表)࿱…...
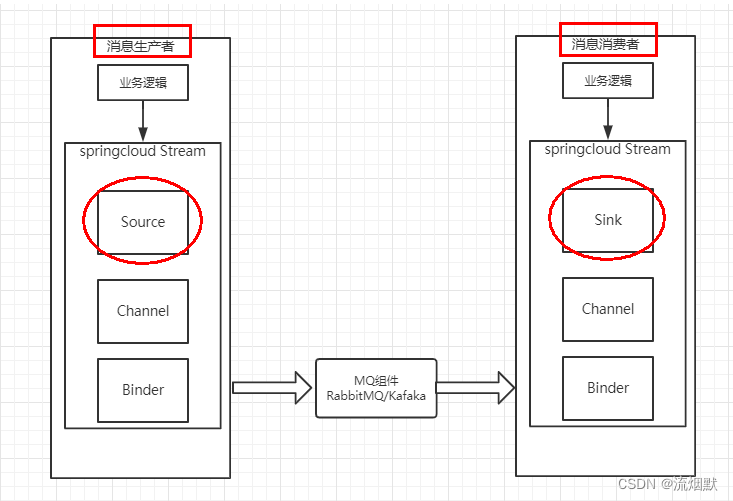
Spring Cloud Stream 消息驱动基础入门与实践总结
Spring Cloud Stream是用于构建与共享消息传递系统连接的高度可伸缩的事件驱动微服务框架,该框架提供了一个灵活的编程模型,它建立在已经建立和熟悉的Spring熟语和最佳实践上,包括支持持久化的发布/订阅、消费组以及消息分区这三个核心概念。…...

你好rust
第一次安装rust,记录一下笔记。 几年前就听说过rust,自己一直是个c爱好者,所以比较抵触rust,早年还有什么rust向上突破群。一直比较抵触,直到这几年rust已经渐渐深入到linux内核、云原生可观测以及zend社区当中&#x…...
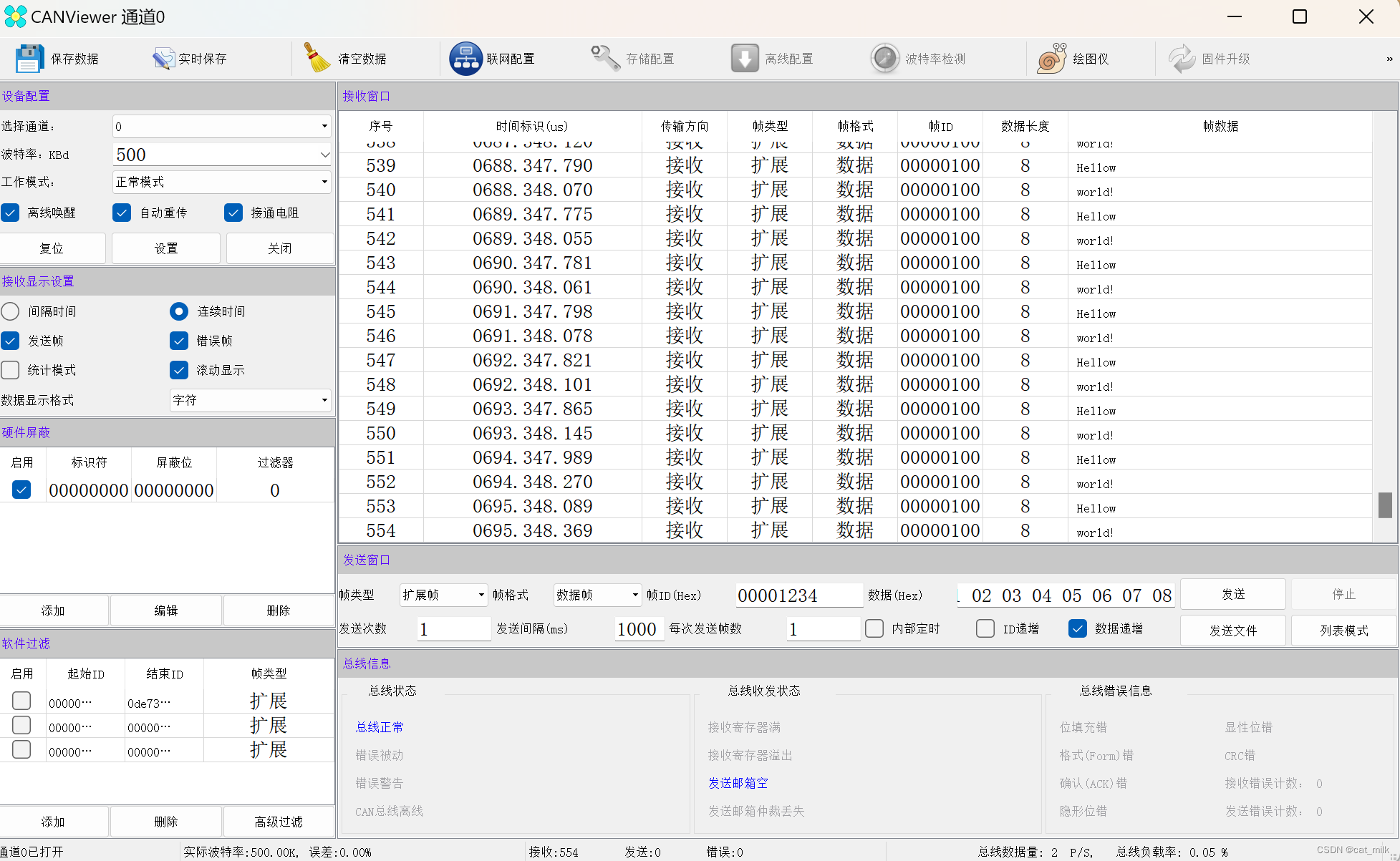
STM32 printf 重定向到CAN
最近在调试一款电机驱动板 使用的是CAN总线而且板子上只有一个CAN 想移植Easylogger到上面试试easylogger的效果,先实现pritnf的重定向功能来打印输出 只需要添加以下代码即可实现 代码 #include <stdarg.h> uint8_t FDCAN_UserTxBuffer[512]; void FDCAN_p…...
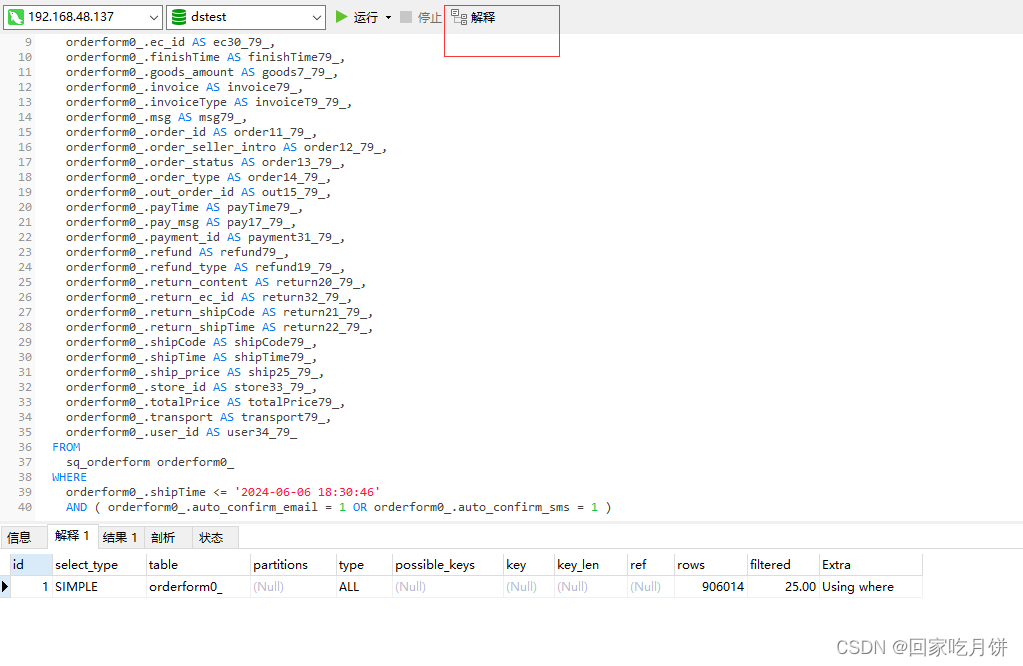
jmeter性能优化之mysql监控sql慢查询语句分析
接上次博客:基础配置 多用户登录并退出jmx文件:百度网盘 提取码:0000 一、练习jmeter脚本检测mysql慢查询 随意找一个脚本(多用户登录并退出),并发数设置300、500后分别查看mysql监控平台 启动后查看,主要查看mysql…...

海南聚广众达电子商务咨询有限公司引领行业变革
在数字化浪潮席卷全球的今天,电商行业正以前所未有的速度发展。海南聚广众达电子商务咨询有限公司,凭借其在抖音电商领域的深厚积累和不断创新,正逐步成为行业的佼佼者。这家以专注、专业、专注为核心理念的公司,不仅为客户提供全…...
Unity API学习之资源的动态加载
资源的动态加载 在实际游戏开发的更新换代中,随着开发的软件不断更新,我们在脚本中需要拖拽赋值的变量会变空,而要想重新拖拽又太花费时间,因此我们就需要用到Resources.Load<文件类型>("文件名")函数来在一开始…...

C++算法——回溯
回溯算法 实现思想 先看一个实例: //暴力枚举的算法 int n 5; for (int a 1; i < n; i) {for (int b 1; b < n; b){for (int c 1; c < n; c){for (int d 1; d < n; d){for (int e 1; e < n; e){//判断 abcde 是否互补相同if (a ! b &&a…...

java的深拷贝和浅拷贝
总结: 深拷贝:无论是基本类型还是引用类型都会创建新的实例。 浅拷贝:对于基本类型就是复制其值,对于引用类型则是复制了指向这些数据类型的内存地址。 浅拷贝(Shallow Copy) 浅拷贝是指在创建新对象时&am…...

AI产品经理,应掌握哪些技术?
美国的麻省理工学院(Massachusetts Institute of Technology)专门负责科技成果转化商用的部门研究表明: 每一块钱的科研投入,需要100块钱与之配套的投资(人、财、物),才能把思想转化为产品&…...

同三维T80004EHL-W-4K30 4K HDMI编码器,支持WEBRTC协议
输入:1路HDMI1路3.5音频,1路HDMI环出1路3.5音频解嵌输出 4K30超高清,支持U盘/移动硬盘/TF卡录制,支持WEBRTC协议,超低延时,支持3个点外网访问 1个主流1个副流输出,可定制选配POE供电模块,WEBR…...

Hi3861 OpenHarmony嵌入式应用入门--点灯
本篇实现对gpio的控制,通过控制输出进行gpio的点灯操作。 硬件 我们来操作IO2,控制绿色的灯。 软件 GPIO API API名称 说明 hi_u32 hi_gpio_deinit(hi_void); GPIO模块初始化 hi_u32 hi_io_set_pull(hi_io_name id, hi_io_pull val); 设置某个IO…...
SaaS案例分享:成功构建销售渠道的实战经验
面对SaaS产品推广的难题,你是否曾感到迷茫,不知如何选择有效的销售渠道?Shopify独立站联盟营销或许能为你提供新的思路。Shopify作为领先的电商解决方案提供商,其独立站功能为众多商家提供了强大的在线销售平台。而联盟营销&#…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
