Score Matching(得分匹配)
Score Matching(得分匹配)是一种统计学习方法,用于估计概率密度函数的梯度(即得分函数),而无需知道密度函数的归一化常数。这种方法由Hyvärinen在2005年提出,主要用于无监督学习,特别是在密度估计和生成模型中。
基本原理
在概率论中,得分函数(Score Function)是概率密度函数关于其参数的梯度。对于一个随机变量 x x x 的概率密度函数 p ( x ) p(x) p(x),其得分函数 ∇ x log p ( x ) \nabla_x \log p(x) ∇xlogp(x) 定义为:
score ( x ) = ∇ x log p ( x ) \text{score}(x) = \nabla_x \log p(x) score(x)=∇xlogp(x)
得分匹配的目标是学习一个模型 q ( x ; θ ) q(x; \theta) q(x;θ),使得模型得分函数 ∇ x log q ( x ; θ ) \nabla_x \log q(x; \theta) ∇xlogq(x;θ) 与真实分布 p ( x ) p(x) p(x) 的得分函数尽可能接近。
得分匹配的损失函数
得分匹配的损失函数定义为模型得分函数与真实得分函数之间的期望差异,通常通过以下形式表示:
L ( θ ) = E x ∼ p ( x ) [ 1 2 ∥ ∇ x log q ( x ; θ ) − ∇ x log p ( x ) ∥ 2 ] L(\theta) = \mathbb{E}_{x \sim p(x)} \left[ \frac{1}{2} \|\nabla_x \log q(x; \theta) - \nabla_x \log p(x)\|^2 \right] L(θ)=Ex∼p(x)[21∥∇xlogq(x;θ)−∇xlogp(x)∥2]
由于我们通常无法直接计算 p ( x ) p(x) p(x) 的得分函数,Hyvärinen提出了一种技巧,通过积分变换,可以将上述损失函数转化为一个无需知道 p ( x ) p(x) p(x) 的表达式:
L ( θ ) = E x ∼ p ( x ) [ 1 2 ∥ ∇ x log q ( x ; θ ) ∥ 2 + ∇ x 2 log q ( x ; θ ) ] L(\theta) = \mathbb{E}_{x \sim p(x)} \left[ \frac{1}{2} \|\nabla_x \log q(x; \theta)\|^2 + \nabla_x^2 \log q(x; \theta) \right] L(θ)=Ex∼p(x)[21∥∇xlogq(x;θ)∥2+∇x2logq(x;θ)]
这意味着我们只需要知道模型 q ( x ; θ ) q(x; \theta) q(x;θ) 的得分函数和二阶导数,就可以计算损失函数。
应用
得分匹配方法在以下领域有广泛应用:
- 密度估计:通过学习一个模型来近似未知的数据分布,无需知道分布的归一化常数。
- 生成模型:在生成模型中,得分匹配可以用于训练模型,使其能够生成与训练数据相似的样本。
- 自编码器:得分匹配可以用于训练自编码器,通过最小化重构误差和正则化项来学习数据的低维表示。
- 深度学习:在深度学习中,得分匹配可以用于训练深度神经网络,特别是当目标分布难以直接建模时。
优点与局限性
优点:
- 无需知道概率密度函数的归一化常数。
- 损失函数易于计算,只需要模型的一阶和二阶导数。
局限性:
- 对于高维数据,计算二阶导数可能非常复杂和计算密集。
- 得分匹配可能对异常值敏感,因为损失函数直接依赖于得分函数。
得分匹配是一种强大的工具,特别是在处理复杂分布和生成模型时。然而,它也需要仔细的实现和参数调整,以确保有效性和稳定性。
举例
让我们通过一个简单的例子来说明得分匹配方法的应用。假设我们有一组来自未知分布的一维数据点,我们的目标是估计这个分布的密度函数。在这个例子中,我们将使用一个简单的模型,如高斯分布,来近似这个未知分布。
步骤1:数据收集
假设我们有一组一维数据点 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn,这些数据点是从某个未知的一维分布中抽取的。
步骤2:模型选择
我们选择一个高斯分布作为我们的模型 q ( x ; θ ) q(x; \theta) q(x;θ),其中 θ = ( μ , σ 2 ) \theta = (\mu, \sigma^2) θ=(μ,σ2) 是模型的参数,表示均值和方差。高斯分布的概率密度函数为:
q ( x ; θ ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) q(x; \theta) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) q(x;θ)=2πσ21exp(−2σ2(x−μ)2)
步骤3:得分函数计算
对于高斯分布,得分函数(即概率密度函数的对数梯度)为:
∇ x log q ( x ; θ ) = x − μ σ 2 \nabla_x \log q(x; \theta) = \frac{x - \mu}{\sigma^2} ∇xlogq(x;θ)=σ2x−μ
步骤4:得分匹配损失函数
得分匹配的损失函数为:
L ( θ ) = E x ∼ p ( x ) [ 1 2 ∥ ∇ x log q ( x ; θ ) ∥ 2 + ∇ x 2 log q ( x ; θ ) ] L(\theta) = \mathbb{E}_{x \sim p(x)} \left[ \frac{1}{2} \|\nabla_x \log q(x; \theta)\|^2 + \nabla_x^2 \log q(x; \theta) \right] L(θ)=Ex∼p(x)[21∥∇xlogq(x;θ)∥2+∇x2logq(x;θ)]
对于高斯分布,这个损失函数可以简化为:
L ( θ ) = E x ∼ p ( x ) [ ( x − μ ) 2 σ 4 + 1 σ 2 ] L(\theta) = \mathbb{E}_{x \sim p(x)} \left[ \frac{(x - \mu)^2}{\sigma^4} + \frac{1}{\sigma^2} \right] L(θ)=Ex∼p(x)[σ4(x−μ)2+σ21]
步骤5:参数估计
我们使用数据点 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn 来估计损失函数 L ( θ ) L(\theta) L(θ) 的期望值。由于我们不知道真实的分布 p ( x ) p(x) p(x),我们使用经验分布来近似期望:
L ( θ ) ≈ 1 n ∑ i = 1 n [ ( x i − μ ) 2 σ 4 + 1 σ 2 ] L(\theta) \approx \frac{1}{n} \sum_{i=1}^n \left[ \frac{(x_i - \mu)^2}{\sigma^4} + \frac{1}{\sigma^2} \right] L(θ)≈n1∑i=1n[σ4(xi−μ)2+σ21]
然后,我们通过最小化这个损失函数来估计参数 θ \theta θ:
θ ^ = arg min θ L ( θ ) \hat{\theta} = \arg\min_{\theta} L(\theta) θ^=argminθL(θ)
步骤6:模型评估
一旦我们估计出了参数 θ ^ \hat{\theta} θ^,我们就可以使用高斯分布 q ( x ; θ ^ ) q(x; \hat{\theta}) q(x;θ^) 来近似未知的数据分布。我们可以通过计算模型在数据点上的对数似然来评估模型的性能。
这个例子展示了得分匹配方法的基本步骤,尽管它是一个简化的版本。在实际应用中,数据可能来自高维分布,模型可能更加复杂(如深度神经网络),并且需要更复杂的优化技术来估计模型参数。
相关文章:
)
Score Matching(得分匹配)
Score Matching(得分匹配)是一种统计学习方法,用于估计概率密度函数的梯度(即得分函数),而无需知道密度函数的归一化常数。这种方法由Hyvrinen在2005年提出,主要用于无监督学习,特别…...

五大维度大比拼:ChatGPT比较文心一言,你的AI助手选择指南
文章目录 一、评估AI助手的五个关键维度二、ChatGPT和文心一言的比较 评估AI助手的五个关键维度,以及ChatGPT和文心一言的比较如下: 一、评估AI助手的五个关键维度 界面友好性 : 评估标准:用户界面是否直观易用,是否…...
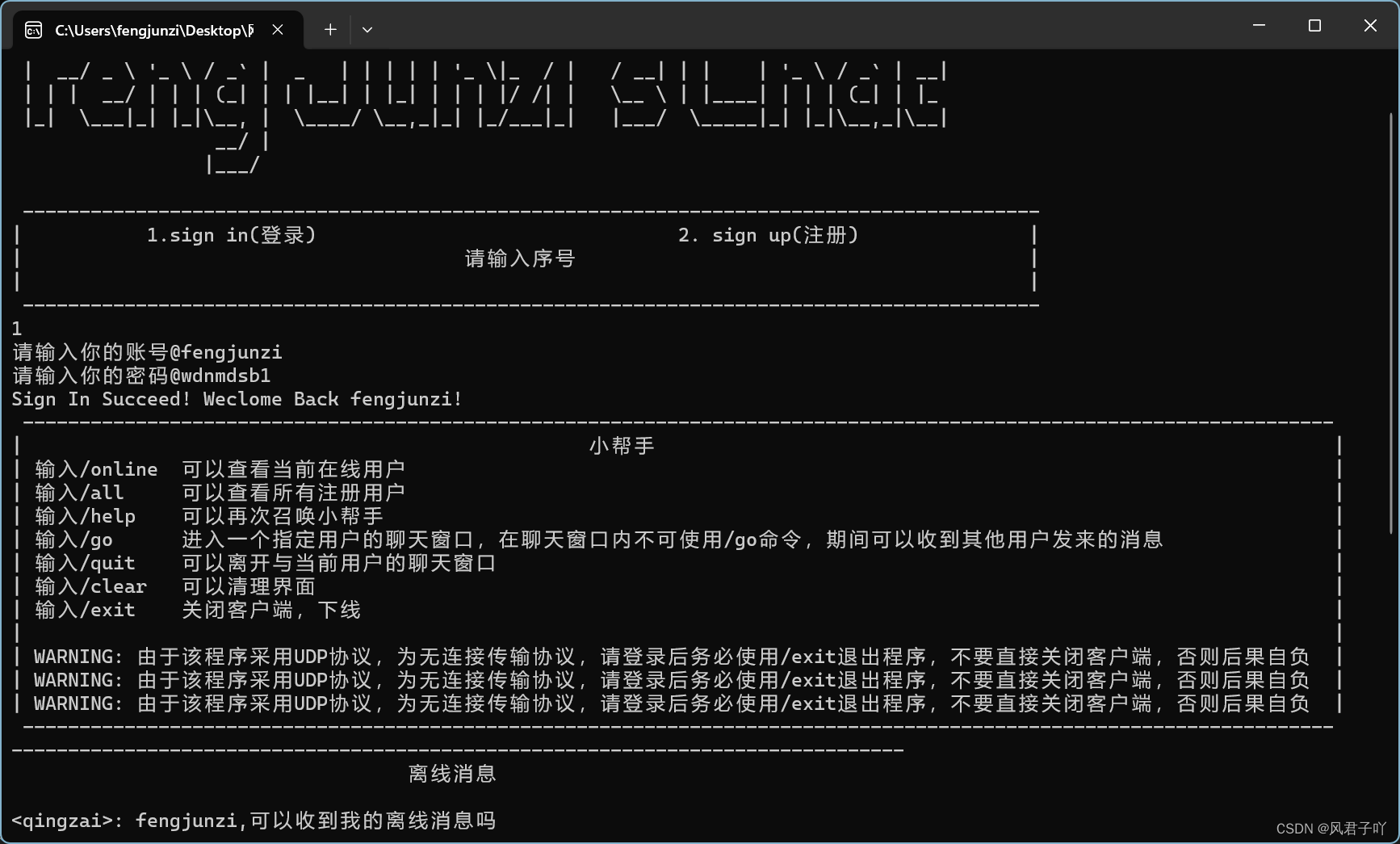
大学课设项目,Windows端基于UDP的网络聊天程序的服务端和客户端
文章目录 前言项目需求介绍一、服务端1.对Udp套接字进行一个封装2. UdpServer的编写3. Task.h4.protocol.h的编写5.线程池的编写6.main.cc 二、客户端1. Socket.h2.protocol.h3.UdpClient4.menu.h5.main.cpp 三、运行图 前言 本次项目可以作为之前内容的一个扩展,学…...

【5.x】ELK日志分析、集群部署
ELK日志分析 一、ELK概述 1、ELK简介 ELK平台是一套完整的日志集中处理解决方案,将ElasticSearch、Logstash和Kiabana三个开源工具配合使用,完成更强大的用户对日志的查询、排序、统计需求。 一个完整的集中式日志系统,需要包含以下几个主…...

揭秘创业加盟:豫腾助力,发掘商机,共赢未来
在我们生活的这个充满活力与机遇的世界里,商业活动如繁星点点,照亮着每个人的创业梦想。 在这个过程中,创业加盟作为一种独特且吸引人的模式,逐渐受到广大创业者的关注。 本文将深入解析创业加盟的精髓,以及如何在其…...
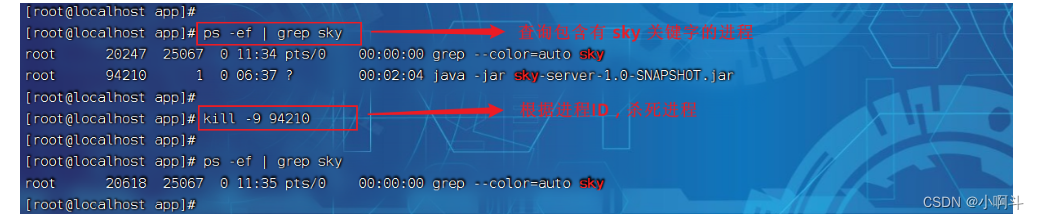
Linux操作系统以及一些操作命令、安装教程
Web课程完结啦,这是Web第一天的课程大家有兴趣可以传送过去学习 http://t.csdnimg.cn/K547r Linux-Day01 课程内容 Linux简介 Linux安装 Linux常用命令 1. 前言 1.1 什么是Linux Linux是一套免费使用和自由传播的操作系统。说到操作系统,大家比…...
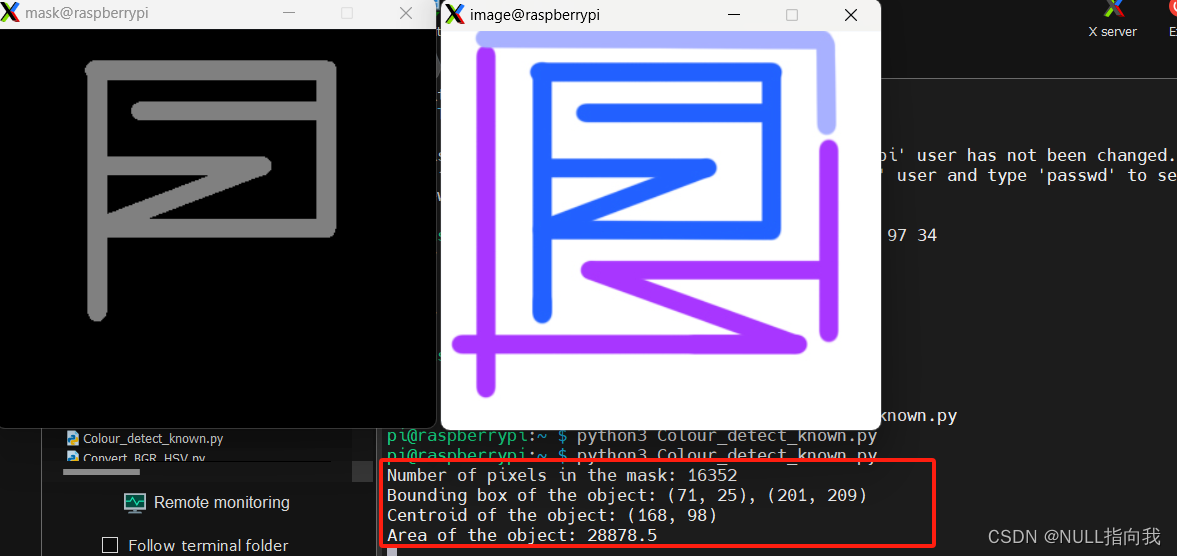
树莓派4B_OpenCv学习笔记6:OpenCv识别已知颜色_运用掩膜
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: 学了这些OpenCv的理论性知识,不进行实践实在…...

ZSH 配置
ZSH 配置 1. 安装 ZSH2. 安装 oh my zsh3. 安装插件3.1 autojump3.2 zsh-autosuggestions 1. 安装 ZSH sudo apt-get install zsh 完成安装后需设置当前用户使用 zsh: chsh -s /bin/zsh 重启后即可使用 2. 安装 oh my zsh 安装 oh my zsh 需先安装 git。 自动安装…...

LogicFlow 学习笔记——5. LogicFlow 基础 主题 Theme
主题 Theme LogicFlow 提供了设置主题的方法,便于用户统一设置其内部所有元素的样式。设置方式有两种: 初始化LogicFlow时作为配置传入初始化后,调用LogicFlow的 setTheme 方法 主题配置参数见主题API 配置 new LogicFlow 时作为将主题配…...

Centos7.9使用kubeadm部署K8S集群
Centos7.9使用kubeadm部署K8S集群 使用kubeadm部署一个k8s集群,单master2worker节点。 1. 环境信息 操作系统:CentOS 7.9.2009内存: 2GBCPU: 2网络: 能够互访,能够访问互联网 hostnameip备注k8s-master192.168.0.51masterk8s-node1192.16…...
)
VB.net调用VC DLL(二)
参考文献5,讲了在C程序中直接调用DLL和lib的函数方法,不是通过编译器连接方式 也讲了在非C程序中直接调用DLL和lib的函数方法。 实操了一下,建了win32dll项目 新建.h文件和.cpp文件 .h文件中加: void __stdcall funcA(double…...

社团管理系统
用Spring Boot、Vue.js和MyBatis实现社团管理系统 温馨提示:项目源代码获取方式见文末 摘要 本文探讨了如何使用Spring Boot作为后端框架,Vue.js作为前端框架,以及MyBatis作为数据库持久层框架,构建一个社团管理系统。该系统旨…...
网站的文章起到什么作用
1.便于用户了解产品服务 如果想要获得更多的用户访问或者转化率,那么网站就得需要高质量、高原创的文章,通过文章可以让用户更好的了解公司的产品和服务,用户会根据自己的需求去选择服务类型,从而可以给公司产生业务订单&am…...

Science | 稀土开采威胁马来西亚的生物多样性
马来西亚是一个生物多样性热点地区,拥有超过17万种物种,其中1600多种处于濒临灭绝的风险。马来西亚的热带雨林蕴藏了大部分的生物多样性,并为全球提供重要的生态系统效益,同时为土著社区带来经济和文化价值。同时马来西亚具有可观…...

pandas read_csv跳过有错的行
在使用Pandas的read_csv函数时,如果遇到格式错误或其他导致读取失败的行,Pandas默认会抛出异常。但如果你想让Pandas自动跳过这些错误行,可以使用error_bad_linesFalse参数。这将使Pandas在遇到格式错误的行时,忽略这些行而不是中…...

VRChat 2024年裁员原因与背景深度分析
VRChat,作为2022年元宇宙/VR社交领域的巨头,近期在2024年宣布裁员计划,其背后原因和背景值得业界尤其是仍在纯元宇宙虚拟空间创业的同仁们重点关注。 一、创始人决策失误 根据CEO的邮件披露,VRChat的创始人因缺乏经验和过度自信…...

mybatisplus 笔记
int isDelete userRoleMapper.delete(new LambdaQueryWrapper<UserRole>().in(UserRole::getUserId, roleUserDTO.getUserId()).in(UserRole::getRoleId, roleUserDTO.getRoleId()));LambdaQueryWrapper<UserRole>: LambdaQueryWrapper 是 MyBatis Plus 提供的一个…...
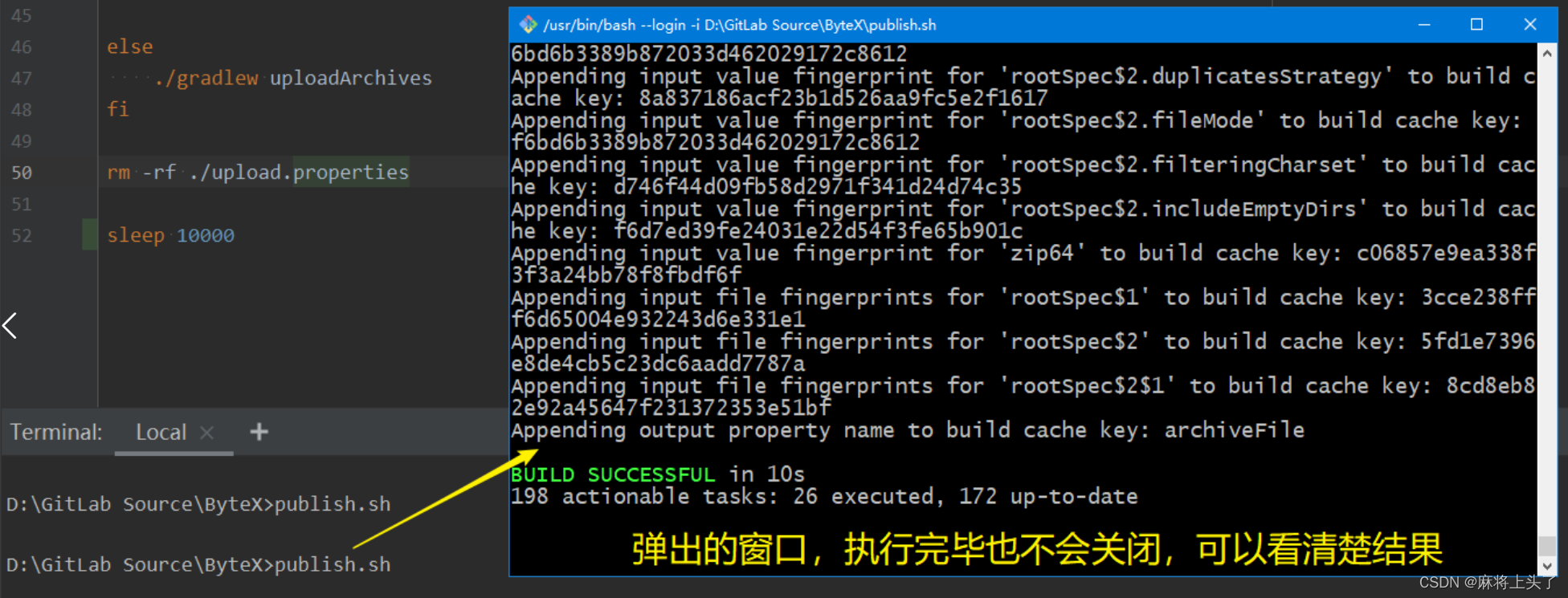
Shell脚本(.sh文件)如何执行完毕之后不自动关闭?
Shell脚本异常傲娇,出错后、执行完根本不给你机会让你查看报错信息、输出信息,直接闪退。 废话不多说,调教方法如下,直接在Shell脚本末尾加上如下代码: 1、实现方式一 1.1 使用read命令达到类似bat中的pause命令效果…...

苏州辰安塑业携塑料托盘、塑料物流箱解决方案亮相2024杭州快递物流展
苏州辰安塑业携塑料托盘、吹塑托盘、塑料卡板箱、塑料周转箱、塑料物流箱、塑料垃圾桶解决方案盛装亮相2024杭州快递物流展! 展位号:3C馆A51 苏州辰安塑业有限公司,是一家专业从事塑料托盘、吹塑托盘、塑料卡板箱、塑料周转箱、塑料物流箱、…...

大模型应用开发技术:Multi-Agent框架流程、源码及案例实战(二)
LlaMA 3 系列博客 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 基于 LlaMA…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
