【数据结构】第十七弹---C语言实现选择排序

✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】【C++详解】
目录
1、选择排序
1.1、基本思想
1.2、代码实现
1.3、代码测试
1.4、时空复杂度分析
总结
1、选择排序
1.1、基本思想
选择排序是一种简单直观的比较排序算法。该算法的基本思想是在每一轮中选出当前未排序部分的最小(或最大)元素,然后将其放置到未排序序列的起始位置,这个过程一直重复直至整个数组被排序。
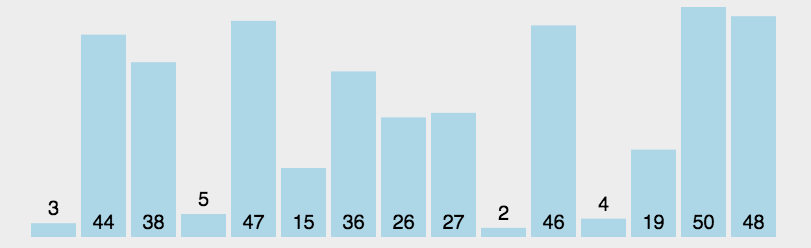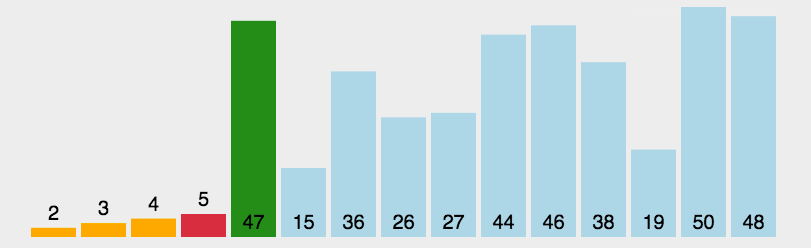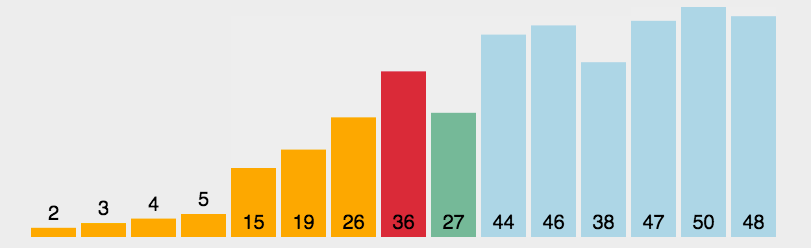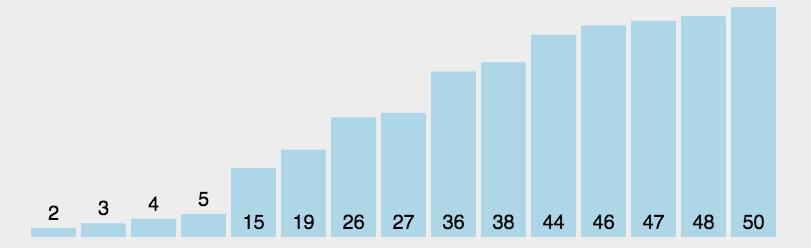
选择排序的具体步骤如下:
★ 从数组的当前未排序部分选择最小(或最大)的一个元素。
★ 将这个最小(或最大)元素与未排序序列的第一个元素交换位置。
★ 然后从剩余未排序的元素中继续这个过程,将每一次找到的最小(或最大)元素放到未排序序列的开始。
★ 这个过程一直进行到整个数组的所有元素都被排为有序状态。
1.2、代码实现
此处可以进行一个小的优化,同时找最小值与最大值,但是有一个细节需要注意,先上代码。
此处还需要交换元素,所以提前封装一个交换函数。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int a[], int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;//找最大值的下标int mini = begin;//找最小值的下标for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);begin++;end--;}
}★ 首先初始化两个索引
begin和end,分别代表当前未排序序列的开始和结束位置。★ 进入一个循环,条件是
begin < end,确保在数组中还有未排序的元素。★ 遍历一遍序列,找到最大元素和最小元素的下标。
★ 将最小元素与序列的始端交换,最大元素与序列的尾端交换。
★ 更新begin与end。
思考一下上面写的代码有没有问题呢???
答案是有问题的,因为这里我们是首先进行最小元素与首位置更换,再进行最大元素与末尾更换,如果我的最大元素就在首位置就会有问题,如下图:
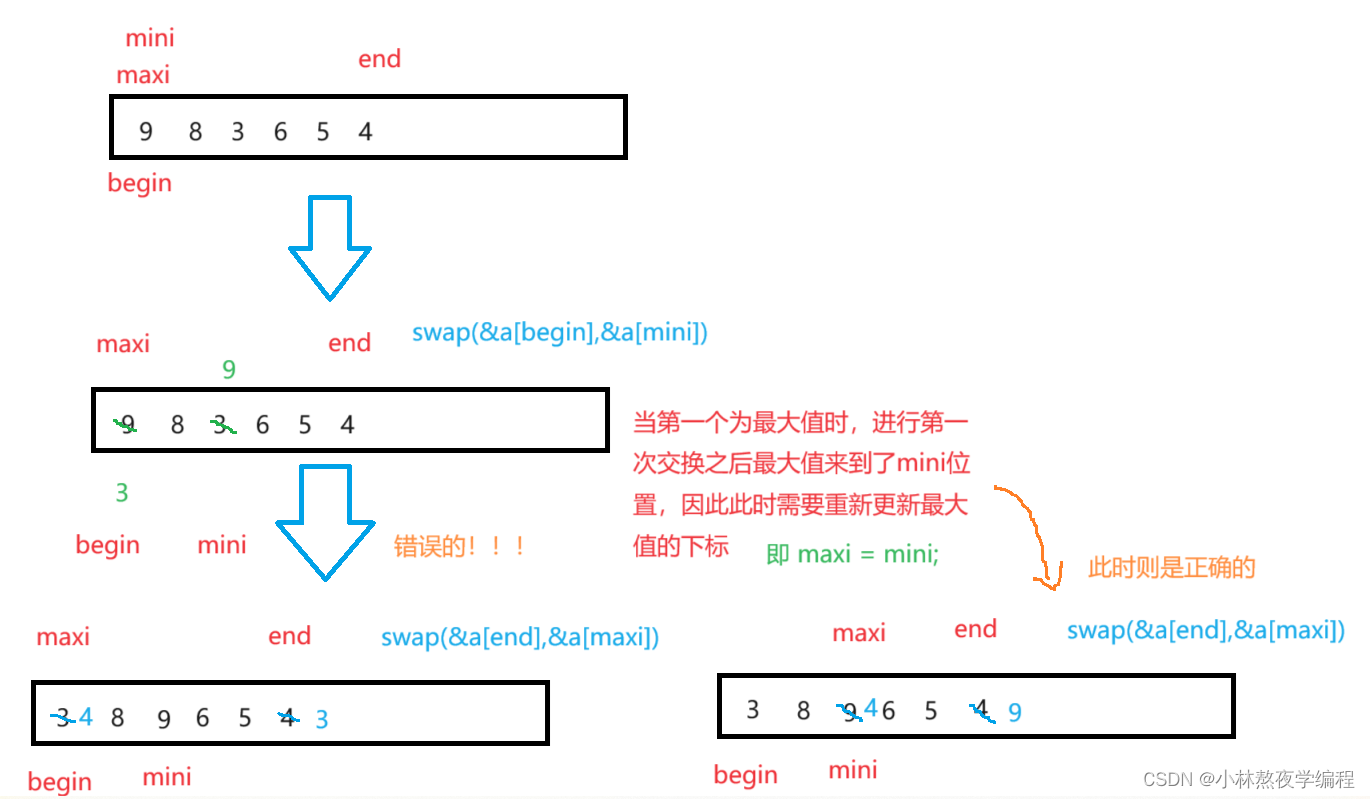
如果最大值就在第一个位置时需要更新最大值的下标!!!
正确的代码如下:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int a[], int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;//找最大值的下标int mini = begin;//找最小值的下标for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);//最大值的位置跟最小值重合//mini被换到maxi位置时 原本的最大值则是miniif (maxi == begin)maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}注意:
1.这里是对最初的选择排序进行优化,最小值最大值一起进行的。
2.当最大值被交换后,需要重新赋值。
1.3、代码测试
测试代码:
//测试选择排序
int main()
{int a[] = { 9,8,7,6,5,4,3,2,1,0 };//给一组数据int sz = sizeof(a) / sizeof(a[0]);//计算数组元素个数printf("排序前:\n");ArrayPrint(a, sz);SelectSort(a, sz);printf("排序后:\n");ArrayPrint(a, sz);return 0;
}测试结果:
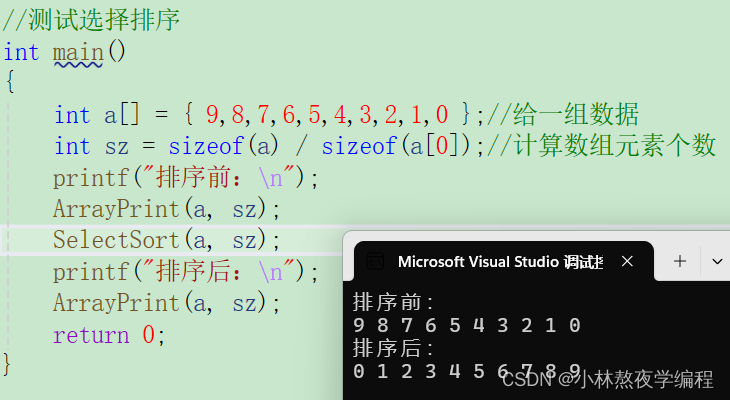
1.4、时空复杂度分析
时间复杂度
最好、平均、最坏情况下的时间复杂度都是 O(n^2)。
原因在于,不管数组的初始顺序如何,选择排序都需要比较所有未排序的元素来找到最小(或最大)的元素,并执行这个过程 n-1 次(对于 n 个元素的数组)。每次选择操作需要比较的次数从 n-1 次减少到 1 次,总共的比较次数是 (n-1) + (n-2) + … + 1 = n(n-1)/2,这是一个二次函数,因此时间复杂度为 O(n^2)。
空间复杂度
选择排序是一种原地排序算法,除了输入数组外,它只需要有限的几个变量(比如,用于存储最小元素下标的变量和循环计数器)。因此,它的空间复杂度为常数空间O(1)。
选择排序的特性总结:
1. 选择排序思考非常好理解,但是效率不是很好。实际中很少使用。
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定5. 复杂性:简单
总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!
相关文章:

【数据结构】第十七弹---C语言实现选择排序
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、选择排序 1.1、基本思想 1.2、代码实现 1.3、代码测试 1.4、时空复杂度分析 总结 1、选择排序 1.1、基本思想 选择排序是一种简单直观的比…...
)
信号处理中的梯型权重操作(Tapering)
目录 1. 引言2. 一个Tapering操作的例子3. Tapering操作的简单实现延伸阅读1. 引言 Tapering 操作是对信号数据在水平和垂直方向上应用梯形权重,这个操作可以减弱数据边界效应,从而在进行傅里叶变换时减少伪影和边缘效应。本文将通过一个简单的例子来展示 Tapering 操作的具…...

深入解析分布式链路追踪:原理、技术及应用
目录 分布式链路追踪简介分布式链路追踪的基本概念 Span 和 Trace上下文传播采样策略 分布式链路追踪的工作原理常见的分布式链路追踪系统 ZipkinJaegerOpenTelemetry 分布式链路追踪的技术实现 数据收集数据传输数据存储数据展示 分布式链路追踪的应用场景 性能优化故障排除依…...

2024信息系统、信号处理与通信技术国际会议(ICISPCT2024)
2024信息系统、信号处理与通信技术国际会议(ICISPCT2024) 会议简介 2024国际信息系统、信号处理与通信技术大会(ICISPCT2024)将在青岛隆重开幕。本次会议旨在汇聚全球信息系统、信号处理和通信技术领域的专家学者,共同探索行业…...

用这个神级提示词插件,能让你的AI绘画工具Stable diffusion提示词直接写中文!
大家好,我是设计师阿威 最近,有同学在使用AI绘画工具 Stable Diffusion的时候和我说:老师,我英文不好,能不能直接让我写中文提示词啊?最好可以直接在SD的输入框就能直接写中文,不用切换网页或者…...

Android里的设计模式
一:设计模式分类 经典的23种设计模式是由Erich Gamma、Richard Helm、Ralph Johnson和John Vlissides(合称“Gang of Four”)在他们的书《设计模式:可复用面向对象软件的基础》中定义的。以下是这些设计模式的分类和简要介绍。 1.…...

token无感刷新
Token无感刷新通常指的是在用户不知情的情况下自动刷新认证Token,以保持用户的会话状态。这通常在使用JWT(JSON Web Tokens)作为认证方式时使用。以下是实现无感刷新的一种常见方法: 1. 前端请求拦截: 在发送请求前&a…...
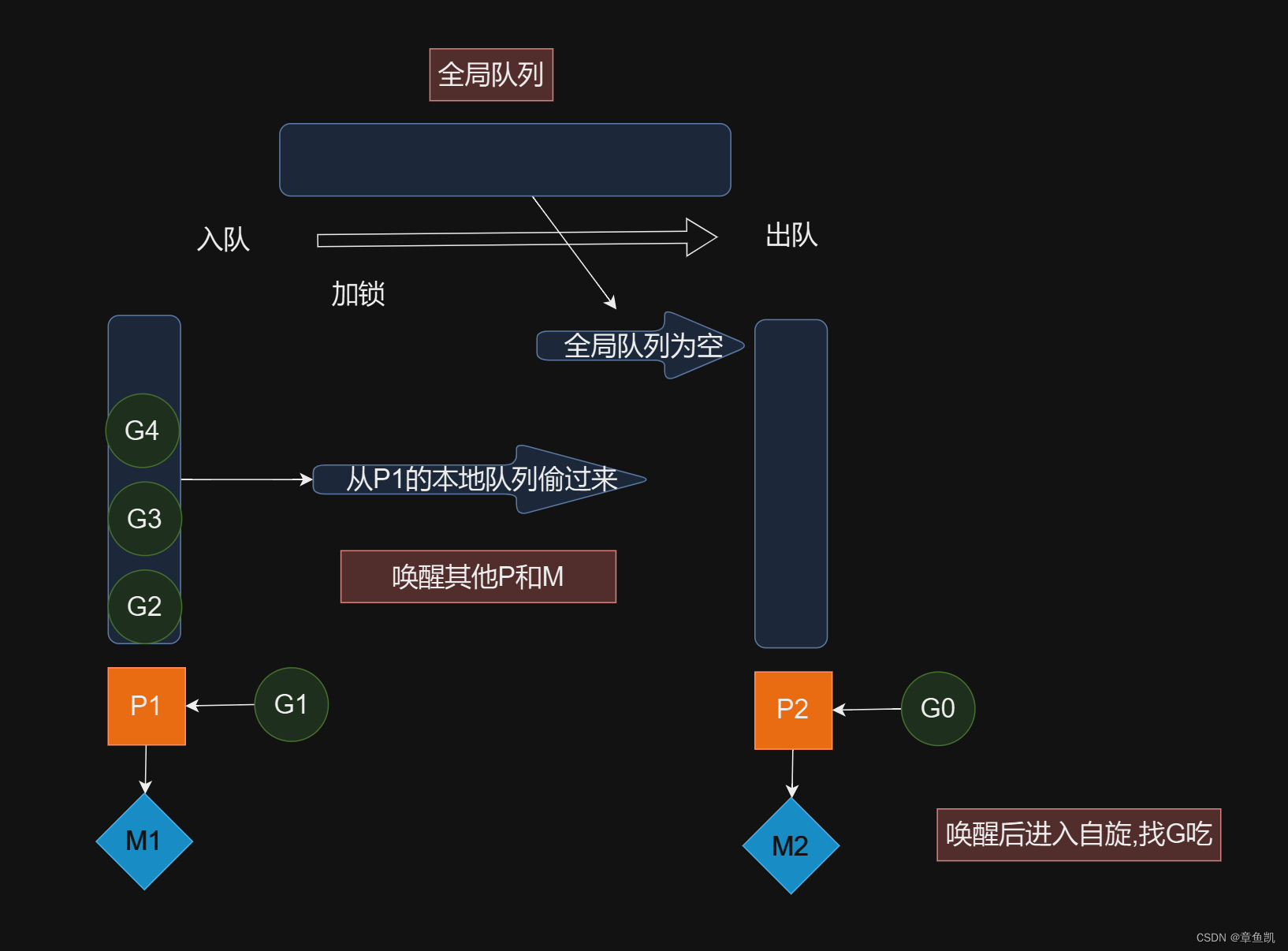
Golang的协程调度器GMP
目录 GMP 含义 设计策略 全局队列 P的本地队列 GMP模型以及场景过程 场景一 场景2 场景三 场景四 场景五 场景六 GMP 含义 协程调度器,它包含了运行协程的资源,如果线程想运行协程,必须先获取P,P中还包含了可运行的G…...

C++ 后端,Vue前端
参考2篇博客 1-VUE、C前后端调用 2-Vue解决CORS header ‘Access-Control-Allow-Origin’ missing及同源、跨域问题 这里给出App.vue代码 <script setup lang"ts"> import HelloWorld from ./components/HelloWorld.vueimport axios from axios import { ref…...

使用Navicat Premium向mysql插入2000000条数据
DELIMITER // DROP PROCEDURE IF EXISTS sys_log; CREATE PROCEDURE sys_log() BEGIN DECLARE n int DEFAULT 1; WHILE(n<2000000) DO INSERT INTO sys_log VALUES (n, 超级系统管理员, 查询实时工况数据, /keyParameterMonitoring/getNewestUnitData, {\"role\"…...

docker命令记录
基本命令和参数 docker run: 运行一个新的容器实例。-itd: 组合参数,含义如下: -i: 以交互模式运行容器,保持标准输入打开。-t: 分配一个伪终端。-d: 后台运行容器,即使容器启动后依然返回控制台。 设备映射 --device/dev/dri…...

Java学习七
Java包 String对象 String案例 集合 ArrayList 集合...
麒麟Kylin | 操作系统的安装与管理
以下所使用的环境为:VMware Workstation 17 Pro、Kylin-Server-10-SP2-x86-Release-Build09-20210524 一、创建虚拟机 在VMware主机单击【创建新的虚拟机】 **在新建虚拟机向导中选择【自定义】,然后点击【下一步】 ** 保持默认选项,然后…...
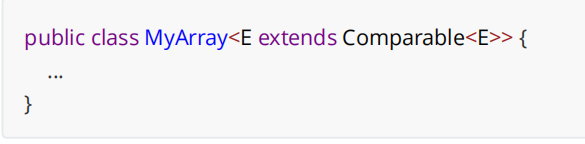
数据结构预备知识(Java):包装类泛型
1、包装类 1.1 包装类 在Java中,每一个基本数据类型都有一个对应的包装类: 在SE的学习中我们已有过简单了解。 我们可以注意到,除了int类型的包装类为Integer,char类型的包装类为Character外,其余基本类型的包装类均…...

掌握Linux Vim:从基础到高级的全面指南
Vim是一款在Linux世界中备受推崇的文本编辑器,它以其强大的功能和高效的操作模式闻名于世。尽管Vim的学习曲线较陡,但一旦掌握,你将发现它在代码编辑和文本处理方面的无与伦比的优势。本文将从Vim的基础知识开始,逐步深入到高级用法和技巧,帮助你全面掌握这款强大的编辑器…...

打好“组合拳”,实现国有企业降本增效
在当前经济不确定性加剧、市场寒意明显的背景下,众多国有企业因历史积累的管理问题而陷入困境。随着经济形势的严峻,各行业普遍出现发展乏力的现象,促使企业开始重视“修炼内功”、“向内挖潜”,试图控制成本,以确保平…...

四川古力未来科技有限公司抖音小店解锁电商新机遇
在数字化浪潮席卷全球的今天,电商行业正以前所未有的速度蓬勃发展。四川古力未来科技有限公司紧跟时代步伐,积极拥抱变革,在抖音平台上开设小店,为品牌发展注入了新的活力。那么,四川古力未来科技有限公司抖音小店究竟…...
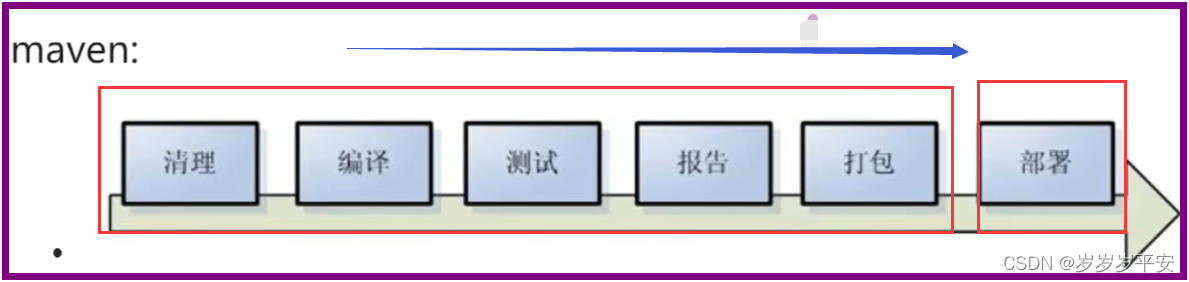
Maven之介绍
目录 一、简介 (2)为什么学习Maven? 二、小结 一、简介 (1)Maven 是一个 Java 项目管理和构建工具。它可以定义项目结构、项目依赖,并使用统一的方式进行自动化构建,是Java项目不可缺少的工具…...

简单了解java中的File类
1、File类 1.1、概述 File对象就表示一个路径,可以是文件路径也可以是文件夹路径,这个路径可以 是存在的,也可以是不存在的。 1.2、常见的构造方法 方法名称说明public File(String pathname)根据文件路径创建文件…...
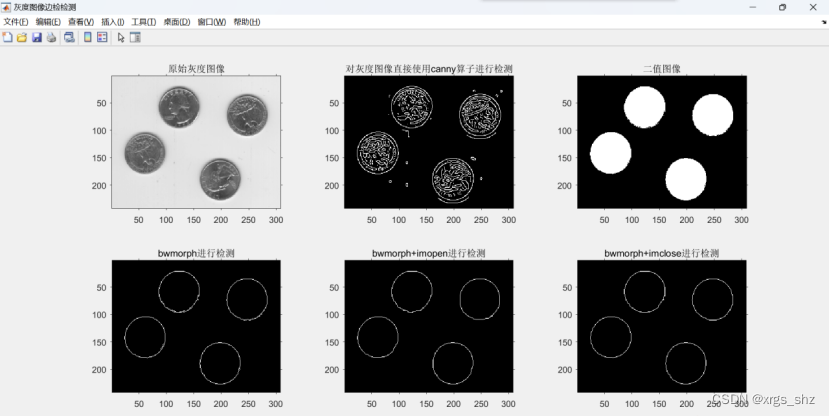
边缘检测(一)-灰度图像边缘检测方法
灰度图像边缘检测是数字图像处理与机器视觉中经常遇到的一个问题,边缘检测是否连续、光滑是判断检测方法优劣的一个重要标准,下面通过一个实例提供灰度图像边缘检测方法,该方法对其他图像检测也具有一定的参考价值。 首先,读入一幅…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
