算法 | 子集数排列树满m叉树二分搜索归并排序快速排序
子集树:O(2^n)
一个序列的所有子集为2^n,即可看成具有2^n个叶节点的满二叉树
int backtrack(int k) //k表示扩展结点在解空间树中所处的层次
{if(k>n) //n标识问题的规模output(x); //x是存放当前解的一维数组if(constraint(k)) //约束函数{ //做相关标识backtrack(k+1)//做相关标识的反操作 } if(bound(k)) //限定函数{//做相关标识backtrack(k+1)//做相关标识的反操作 }}常用于:解空间为子集树的常见问题:
(1)0-1背包问题;
(2)子集和问题;
(3)装载问题;
(4)最大团问题。
排序树:O(n!)
int backtrack(int t) //t表示扩展结点在解空间树中所处的层次
{if(t>n) //n标识问题的规模output(x); //x是存放当前解的一维数组else{for(int i=t;i<=n;i++){swap(x[t],x[i]); //实现两个位置的交换if(constraint(t)&&bound(t)) //约束函数与限定函数backtrack(t+1) //递归swap(x[t],x[i]); //恢复原状}}}
解空间为排列树的常见问题:
(1)n皇后问题;
(2)旅行商问题;
(3)园排列问题;
(4)电路板排列问题。
满m叉树:O(n*m^n)
地图着色问题:
每个元素有M种选择
二分搜索法:最好:O(1) 最坏:O(logn)
二分搜索法(Binary Search)是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。
最好时间复杂度:
在二分搜索法中,如果我们要查找的元素正好是数组的中间元素,那么我们只需要一次比较就能找到它。因此,最好的情况下,二分搜索的时间复杂度是 O(1)。但是,严格来说,我们通常说二分搜索的最好时间复杂度是 O(log n),因为这只是平均情况或最好情况的一种特例,而平均情况或最好情况通常需要 log n 次比较(当 n 是数组的长度时)。最坏时间复杂度:
在二分搜索法中,最坏的情况是我们要查找的元素不在数组中,或者它在数组的最左边或最右边。在这种情况下,我们需要不断地缩小搜索范围,直到搜索范围为空。每次比较,我们都将搜索范围减半,因此,在最坏的情况下,我们需要 log n 次比较(这里 log 是以 2 为底的对数)。所以,二分搜索的最坏时间复杂度是 O(log n)。
归并排序
#include <iostream>
using namespace std;void Merge(int A[], int low, int mid, int high)
{int* B = new int[high - low + 1];int i = low, j = mid + 1, k = 0;while (i <= mid && j <= high){if (A[i] <= A[j])B[k++] = A[i++];elseB[k++] = A[j++];}while (i <= mid) B[k++] = A[i++];while (j <= high) B[k++] = A[j++];// 修正:复制B到A时,确保k从0开始 for (int p = 0; p < k; p++)A[low + p] = B[p]; // 使用low + p来确保复制到正确的位置 delete[] B; // 释放动态分配的内存
}void MergeSort(int A[], int low, int high)
{if (low < high){int mid = (low + high) / 2;// 修正:递归调用应该包括mid MergeSort(A, low, mid);MergeSort(A, mid + 1, high);Merge(A, low, mid, high);}
}int main()
{int a[] = { 1, 2, 54, 25, 76, 23 };int n = sizeof(a) / sizeof(a[0]); // 计算数组长度 MergeSort(a, 0, n - 1); // 修正:传入正确的high值 for (int i = 0; i < n; i++) // 修正:打印所有元素 cout << a[i] << " "; // 添加空格分隔符 cout << endl; // 打印换行符 return 0;
}这三行代码是归并排序(Merge Sort)算法中的关键步骤。归并排序是一种分治(Divide and Conquer)策略的排序算法。
MergeSort(A, low, mid);这行代码是递归地调用归并排序函数本身,用于对数组的左半部分进行排序。这
2.MergeSort(A, mid + 1, high);这行代码与第一行类似,但它是用于对数组的右半部分进行排序。
3.Merge(A, low, mid, high);当左半部分和右半部分都已经被排序后,这行代码用于将这两个已排序的子数组合并成一个已排序的完整数组。
快速排序
void QuickSort(int array[], int low, int high) {int i = low; int j = high;if(i >= j) {return;}int temp = array[low];while(i != j) {while(array[j] >= temp && i < j) {j--;}while(array[i] <= temp && i < j) {i++;}if(i < j) {swap(array[i], array[j]);}}//将基准temp放于自己的位置,(第i个位置)swap(array[low], array[i]);QuickSort(array, low, i - 1);QuickSort(array, i + 1, high);
}相关文章:

算法 | 子集数排列树满m叉树二分搜索归并排序快速排序
子集树:O(2^n) 一个序列的所有子集为2^n,即可看成具有2^n个叶节点的满二叉树 int backtrack(int k) //k表示扩展结点在解空间树中所处的层次 {if(k>n) //n标识问题的规模output(x); //x是存放当前解的一维数组if(constraint(k)…...

SpringBoot配置第三方专业缓存技术jetcache方法缓存方案
jetcache方法缓存 我们可以给每个方法配置缓存方案 JetCache 是一个基于 Java 的缓存库,支持多种缓存方案和缓存策略,主要用于提升应用程序的性能和响应速度。它提供了多种缓存模式和特性,可以根据需求选择合适的缓存方案。 JetCache 的主…...
游戏开发丨基于PyGame的消消乐小游戏
文章目录 写在前面PyGame消消乐注意事项系列文章写在后面 写在前面 本期内容:基于pygame实现喜羊羊与灰太狼版消消乐小游戏 下载地址:https://download.csdn.net/download/m0_68111267/88700193 实验环境 python3.11及以上pycharmpygame 安装pygame…...
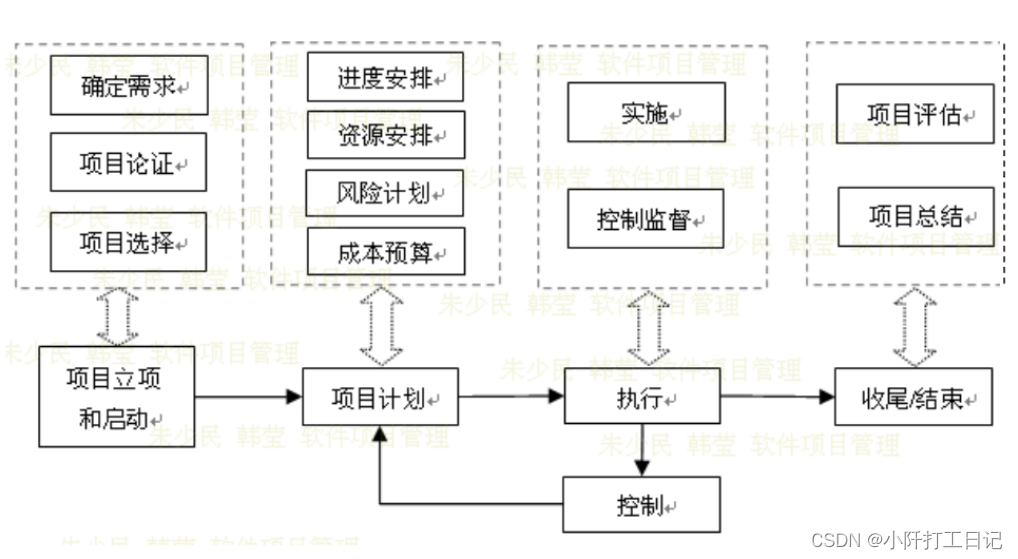
软件项目管理概述
1.什么是项目? 2.项目管理的定义 3.项目管理的本质 4.项目成功的标志 5.项目管理的基本方法 6.项目的生命周期(启动 计划 执行 控制 结束) 7.结合生活中的某件事,谈谈项目管理的作用 项目管理在日常生活中扮演着重要的角色&…...

FastAdmin后台开发框架 lang 任意文件读取漏洞复现
0x01 产品简介 FastAdmin是一款基于PHPBootstrap的开源后台框架,专为开发者精心打造。它基于ThinkPHP和Bootstrap两大主流技术构建,拥有完善的权限管理系统和一键生成CRUD等强大功能。FastAdmin致力于提高开发效率,降低开发成本,…...

数字时代PLM系统的重要性
什么是 PLM(产品生命周期管理)? 从最基本的层面上讲,产品生命周期管理 (PLM)是管理产品从最初构思、开发、服务和处置的整个过程的战略流程。换句话说,PLM 意味着管理产品从诞生到消亡所涉及的一切。 什么是 PLM 软件…...

安卓实现圆形按钮轮廓以及解决无法更改按钮颜色的问题
1.实现按钮轮廓 在drawable文件新建xml文件 <shape xmlns:android"http://schemas.android.com/apk/res/android"<!--实现圆形-->android:shape"oval"><!--指定内部的填充色--><solid android:color"#FFFFFF"/><!-…...

常用原语介绍
1.在Xilinx的example(wavegen example)中看到他们的顶层模块的输入输出管脚都手动例化原语IBUF以及OBUF——工具也会自动给我们加上不必要自己加 2.非mrcc个srcc的管脚输入的时钟信号,无法进入mmcm和bufg————试验过会报错 3.实际上&…...
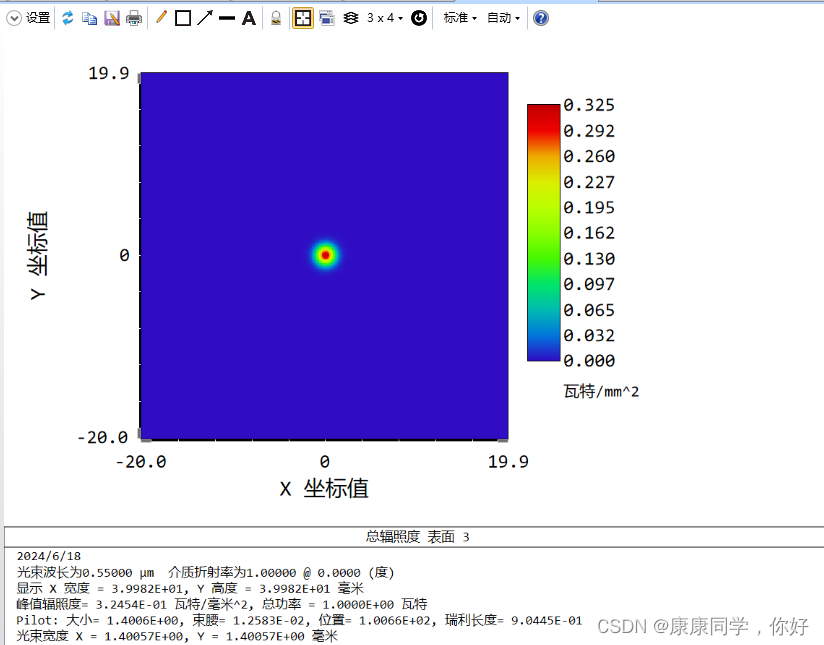
29. 透镜阵列
导论: 物理传播光学(POP)不仅可以用于简单系统,也可以设计优化复杂的光学系统,比如透镜阵列。 设计流程: 透镜阵列建模 在孔径类型中选择“入瞳直径”,并输入2 在视场设定中。设置一个视场&…...

深入理解并打败C语言难关之一————指针(3)
前言: 昨天把指针最为基础的内容讲完了,并且详细说明了传值调用和传址调用的区别(这次我也是做到了每日一更,感觉有好多想写的但是没有写完),下面不多废话,下面进入本文想要说的内容 目录&#…...
Ubuntu-24.04-live-server-amd64启用ssh
系列文章目录 Ubuntu-24.04-live-server-amd64安装界面中文版 Ubuntu安装qemu-guest-agent Ubuntu乌班图安装VIM文本编辑器工具 文章目录 系列文章目录前言一、输入安装命令二、使用私钥登录(可选)1.创建私钥2.生成三个文件说明3.将公钥复制到服务器 三…...
)
Leetcode 2786. 访问数组中的位置使分数最大(DP 优化)
Leetcode 2786. 访问数组中的位置使分数最大 DP 以每个位置为结尾的序列的分数取决于前方的分数,根据奇偶性计算,取最大值 超时 class Solution {public long maxScore(int[] nums, int x) {int n nums.length;long dp[] new long[n];Arrays.fill(dp…...

【docker实战】使用Dockerfile的COPY拷贝资源遇到的问题
事情是这样的。 在我负责的golang项目中,使用硬代码验证某块逻辑。比如: 于是,为了解决硬代码的问题,我制作了表格工具:【开源项目】Excel数据表自动生成工具v1.0版 – 经云的清净小站 (skycreator.top)。 使用表格工…...

如何用多线程执行 unittest 测试用例实现方案
前言 使用python做过自动化测试的小伙伴,想必都知道unittest和pytest这两个单元测试框架,其中unittest是python的官方库,功能相对于pytest来要逊色不少,但是uniitest使用上手简单,也受到的很多的小伙伴喜爱。一直以来都…...

Ascend310 EP模式下容器内进行推理测试
EP模式下容器内进行推理测试 本文的软硬件环境如下: 机器:x86台式机一台 OS: 5.4.0-26-generic Ubuntu20.04 LTS 推理卡:DLAP200-HP-2(凌华基于atlas200模块打造的两模块推理卡) 1. 推理卡固件和驱动安…...
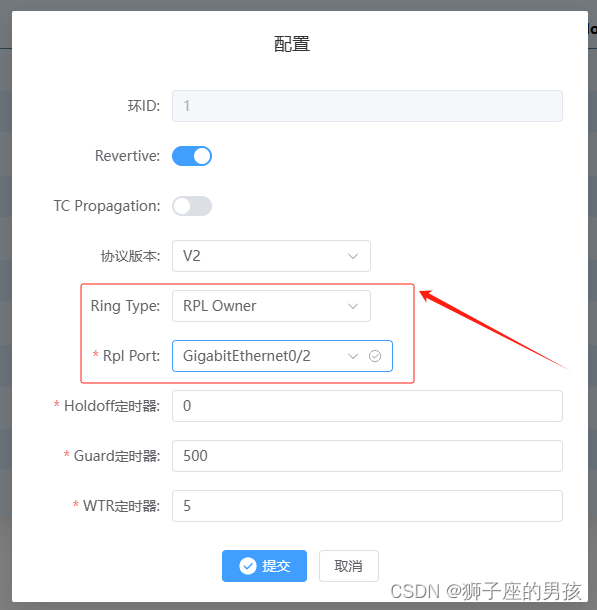
(el-Transfer)操作(不使用 ts):Element-plus 中 Select 组件动态设置 options 值需求的解决过程
Ⅰ、Element-plus 提供的Select选择器组件与想要目标情况的对比: 1、Element-plus 提供Select组件情况: 其一、Element-ui 自提供的Select代码情况为(示例的代码): // Element-plus 提供的组件代码: <template><div class"f…...

Java基础之Math与Array类与System
文章目录 一、Math.random()二、Arrays.binarySearch()三、asList()四、System tip:以下是正文部分 一、Math.random() a < num < b int num (int)(Math.random() * (b - a 1)) a二、…...
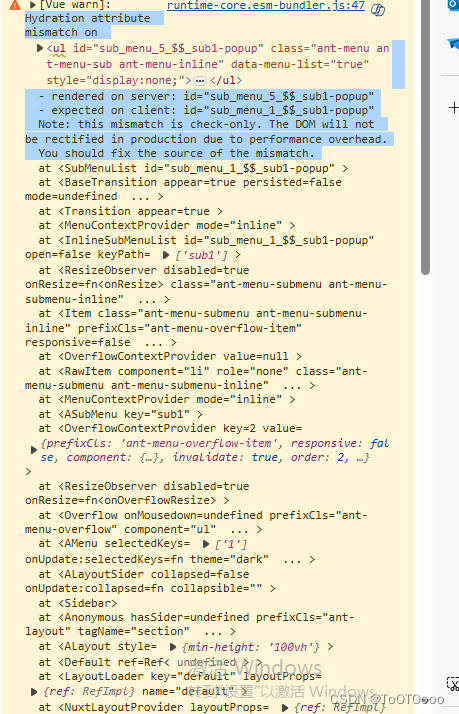
警告:Hydration attribute mismatch on Note: this mismatch is check-only.(水合不匹配)
vue3Nuxt3运行代码是提示如下警告 [Vue warn]: Hydration attribute mismatch on <ul id"sub_menu_5_$$_sub1-popup" class"ant-menu ant-menu-sub ant-menu-inline" data-menu-list"true" style"display:none;">…...

【机器学习】CART决策树算法的核心思想及其大数据时代银行贷款参考案例——机器认知外界的重要算法
目录 引言 概述 CART决策树的特点 核心思想 减少不确定性的指标 基尼系数(Gini Index) 分类错误率 熵 银行实例 背景 数据准备 模型构建 模型评估与优化 应用与结果 代码示例 ✈✈✈✈引言✈✈✈✈ CART算法既可以用于分类问题࿰…...

编程软件是由什么编程的
编程软件是由什么编程的 在数字化的世界里,编程软件作为构建数字生态的基石,其背后所蕴含的奥秘往往令人感到困惑。那么,这些编程软件究竟是由什么编程的呢?这背后隐藏着怎样的逻辑与技术?接下来,我们将从…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
