深度神经网络——什么是降维?
引言
什么是降维? 降维是用于降低数据集维度的过程,采用许多特征并将它们表示为更少的特征。 例如,降维可用于将二十个特征的数据集减少到仅有几个特征。 降维通常用于无监督学习任务
降维是一个用于降低数据集维度的过程,采用许多特征并将它们表示为更少的特征。 例如,降维可用于将二十个特征的数据集减少到仅有几个特征。 降维常用于 无监督学习 从许多功能中自动创建类的任务。 为了更好地理解 为什么以及如何使用降维,我们将了解与高维数据相关的问题以及最流行的降维方法。
更多维度导致过度拟合
维度是指数据集中的特征/列的数量。
人们通常认为,在机器学习中,特征越多越好,因为它可以创建更准确的模型。然而,更多的功能并不一定意味着更好的模型。
数据集的特征对于模型的有用程度可能有很大差异,其中许多特征并不重要。 此外,数据集包含的特征越多,需要的样本就越多,以确保数据中能够很好地表示特征的不同组合。 因此,样本数量与特征数量成比例增加。 更多的样本和更多的特征意味着模型需要更加复杂,并且随着模型变得更加复杂,它们对过度拟合变得更加敏感。 该模型对训练数据中的模式学习得很好,但无法推广到样本数据之外。
降低数据集的维数有几个好处。 如前所述,更简单的模型不太容易过度拟合,因为模型必须对特征之间的相互关系做出更少的假设。 此外,维度越少意味着训练算法所需的计算能力就越少。 类似地,维度较小的数据集需要较少的存储空间。 降低数据集的维数还可以让您使用不适合具有许多特征的数据集的算法。
常见的降维方法
降维可以通过特征选择或特征工程来实现。 特征选择是工程师识别数据集最相关特征的地方,而 特征工程 是通过组合或改造其他特征来创建新特征的过程。
特征选择和工程可以通过编程或手动完成。 当手动选择和设计特征时,通常会通过可视化数据来发现特征和类之间的相关性。 以这种方式进行降维可能非常耗时,因此一些最常见的降维方法涉及使用 Scikit-learn for Python 等库中提供的算法。 这些常见的降维算法包括:主成分分析(PCA)、奇异值分解(SVD)和线性判别分析(LDA)。
用于无监督学习任务降维的算法通常是 PCA 和 SVD,而用于监督学习降维的算法通常是 LDA 和 PCA。在监督学习模型的情况下,新生成的特征仅被输入到机器学习分类器中。请注意,此处描述的用途只是一般用例,而不是这些技术可能使用的唯一条件。上述降维算法只是统计方法,它们在机器学习模型之外使用。
主成分分析

主成分分析(PCA) 是一种统计方法,分析数据集的特征/特征并总结最有影响力的特征。 数据集的特征组合在一起形成表示,该表示保留了数据的大部分特征,但分布在较少的维度上。 您可以将其视为将数据从较高维度的表示形式“压缩”为只有几个维度的表示形式。
作为 PCA 可能有用的情况的一个例子,请考虑描述葡萄酒的各种方式。 虽然可以使用许多高度具体的特征(例如二氧化碳水平、通气水平等)来描述葡萄酒,但在尝试识别特定类型的葡萄酒时,这些具体特征可能相对无用。 相反,根据味道、颜色和年龄等更一般的特征来识别类型会更加谨慎。 PCA可用于组合更具体的特征并创建更通用、有用且不太可能导致过度拟合的特征。
PCA 的执行方式是确定输入特征之间的平均值如何变化,并确定特征之间是否存在任何关系。 为了做到这一点,创建一个协变矩阵,建立一个由关于数据集特征的可能对的协方差组成的矩阵。 这用于确定变量之间的相关性,负协方差表示逆相关,正相关表示正相关。
数据集的主要(最有影响力)组成部分是通过创建初始变量的线性组合来创建的,这是在线性代数概念的帮助下完成的 特征值和特征向量。 创建组合是为了使主成分彼此不相关。 初始变量中包含的大部分信息被压缩到前几个主成分中,这意味着已经创建了新特征(主成分),其中包含较小维空间中的原始数据集的信息。
奇异值分解

奇异值分解(SVD) is 用于简化矩阵中的值,将矩阵简化为其组成部分,并使该矩阵的计算变得更容易。 SVD 可用于实值矩阵和复数矩阵,但出于本说明的目的,我们将研究如何分解实值矩阵。
假设我们有一个由实值数据组成的矩阵,我们的目标是减少矩阵内的列/特征的数量,类似于 PCA 的目标。 与 PCA 一样,SVD 会压缩矩阵的维数,同时尽可能保留矩阵的可变性。 如果我们想对矩阵 A 进行操作,我们可以将矩阵 A 表示为另外三个矩阵,称为 U、D 和 V。矩阵 A 由原始 x * y 元素组成,而矩阵 U 由元素 X * X 组成(它是正交矩阵)。 矩阵 V 是包含 y * y 元素的不同正交矩阵。 矩阵 D 包含元素 x * y,它是一个对角矩阵。
为了分解矩阵 A 的值,我们需要将原始奇异矩阵值转换为新矩阵中找到的对角线值。 使用正交矩阵时,即使乘以其他数字,它们的属性也不会改变。 因此,我们可以利用这个性质来近似矩阵A。 当我们将正交矩阵与矩阵 V 的转置相乘时,结果是与原始 A 等效的矩阵。
当矩阵 a 分解为矩阵 U、D 和 V 时,它们包含矩阵 A 中找到的数据。但是,矩阵的最左边的列将包含大部分数据。 我们可以只取前几列,并得到矩阵 A 的表示形式,该矩阵的维度要少得多,并且 A 中包含大部分数据。
线性判别分析
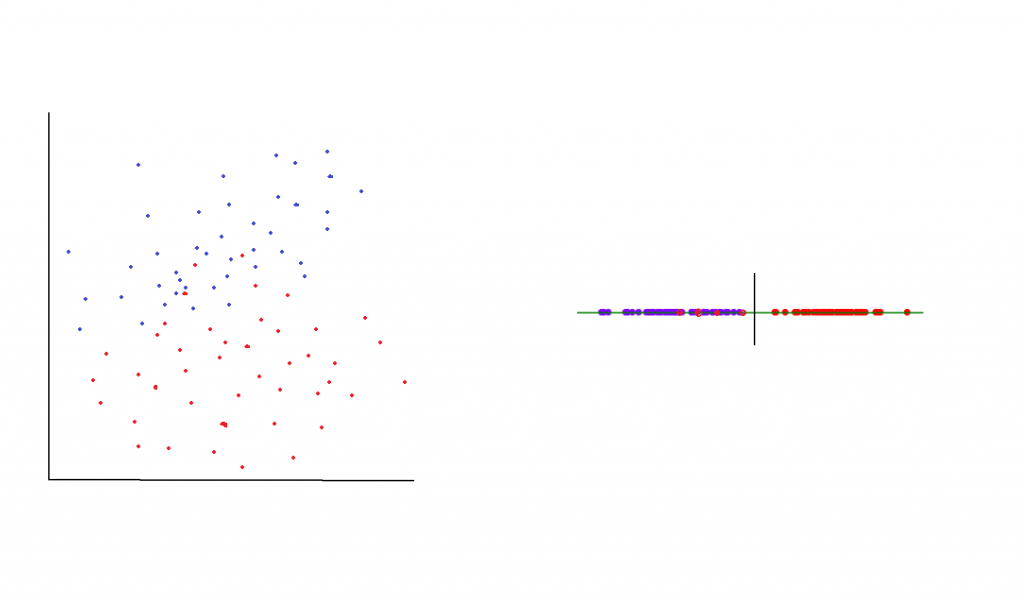
左:LDA 之前的矩阵,右:LDA 之后的轴,现在可分离
线性判别分析(LDA) 是一个从多维图中获取数据的过程 将其重新投影到线性图上。 您可以通过考虑一个充满属于两个不同类的数据点的二维图来想象这一点。 假设这些点分散在各处,因此无法绘制出能够整齐地分隔两个不同类的线。 为了处理这种情况,可以将二维图中找到的点简化为一维图(一条线)。 这条线将分布所有数据点,并且有望将其分为两部分,以实现数据的最佳分离。
执行 LDA 时有两个主要目标。 第一个目标是最小化类别的方差,而第二个目标是最大化两个类别的均值之间的距离。 这些目标是通过创建将存在于二维图中的新轴来实现的。 新创建的轴用于根据前面描述的目标分隔两个类。 创建轴后,在 2D 图中找到的点将沿轴放置。
将原始点沿新轴移动到新位置需要三个步骤。 第一步,使用各个类之间的距离均值(类间方差)来计算类的可分离性。 在第二步中,通过确定相关类别的样本与平均值之间的距离来计算不同类别内的方差。 在最后一步中,创建最大化类之间方差的低维空间。
当目标类的均值彼此相距较远时,LDA 技术可获得最佳结果。 如果分布的均值重叠,LDA 无法使用线性轴有效地分离类别。
相关文章:

深度神经网络——什么是降维?
引言 什么是降维? 降维是用于降低数据集维度的过程,采用许多特征并将它们表示为更少的特征。 例如,降维可用于将二十个特征的数据集减少到仅有几个特征。 降维通常用于无监督学习任务 降维是一个用于降低数据集维度的过程,采用许…...

SpringMVC—RequestMapping注解
一、RequestMapping注解 RequestMapping注解:是Spring MVC框架中的一个控制器映射注解,用于将请求映射到相应的处理方法上,具体来说,他可以将指定URL的请求绑定到一个特定的方法或类上,从而实现对请求的处理和响应。 …...

Java线程池基本概念
全局和局部线程池 全局线程池 在Spring框架中,全局线程池如ThreadPoolTaskExecutor通常是作为Spring Bean存在的,它们的生命周期由Spring容器管理。当Spring容器关闭时,这些线程池也会被适当地清理和关闭。因此,开发者通常不需要手…...

智能车联网安全发展形势、挑战
一、技术演进加速车联网安全环境复杂变化 当前,5G、大数据、大算力、大模型等技术正加速在车联网领域实现融合应用。车联网的网络通信能力、感知计算水平以及创新业务应用都在快速发展,与此同时,车联网的网络安全环境也在随之演进变化&#…...

AWS概述
AWS概述EMR Serverless Aamzon Web Services提供了一系列全球范围的云产品,包括计算、存储、数据库、分析、网络、移动、开发工具、管理工具、IoT、安全和企业应用:按需交付、及时可用、采用随用随付的定价模式。你可以畅享200多种服务,从数据…...
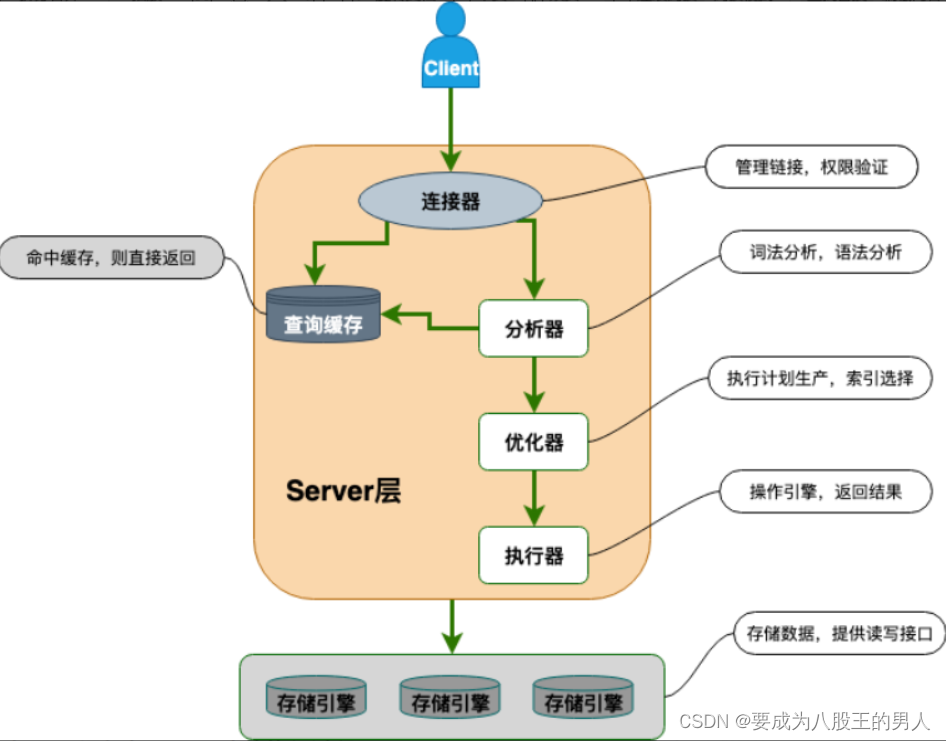
MySQL常见面试题自测
文章目录 MySQL基础架构一、说说 MySQL 的架构?二、一条 SQL语句在MySQL中的执行过程 MySQL存储引擎一、MySQL 提供了哪些存储引擎?二、MySQL 存储引擎架构了解吗?三、MyISAM 和 InnoDB 的区别? MySQL 事务一、何谓事务࿱…...

c语言回顾-函数递归
1.递归的介绍 1.1什么是递归 递归是指在一个函数的定义中调用自身的过程。简单来说,递归是一种通过重复调用自身来解决问题的方法。 递归包括两个关键要素:基本情况和递归情况。基本情况是指当问题达到某个特定条件时,不再需要递归调用&am…...
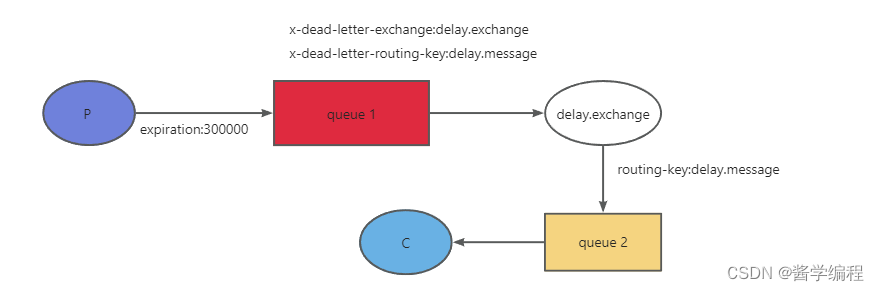
消息队列-RabbitMQ-延时队列实现
死信队列 DLX,全称为Dead-Letter-Exchange,死信交换机,死信邮箱。当消息在一个队列中变成死信之后,它能重新发送到另外一个交换器中,这个交换器就是DLX,绑定DLX的队列就称为死信队列。 导致死信的几种原因: ● 消息…...

【热门开源项目推荐】满足不同程序员的需求与关注点
目录 前言一、热门开源项目介绍二、使用开源热门项目的优势(一)经济方面(二)技术方面(三)社区支持及协作方面 三、程序员选择项目模型建议(一)关键步骤(二)示…...
)
一文理清GO语言日志库实现开发项目中的日志功能(rotatelogs/zap分析)
一文理清GO语言日志库实现开发项目中的日志功能(rotatelogs/zap分析) rotatelogs rotatelogs 是一个用于管理日志文件的 Go 语言库,它提供了自动轮换、压缩和删除旧日志文件的功能。这个库可以帮助你更好地管理和维护你的应用程序日志。要使…...
【Go语言精进之路】构建高效Go程序:了解string实现原理并高效使用
🔥 个人主页:空白诗 🔥 热门专栏:【Go语言精进之路】 文章目录 引言一、Go语言的字符串类型1.1 字符串的定义1.2 字符串的零值可用1.3 字符串的不可变性1.4 字符串的拼接1.5 字符串的常用方法1.6 实际使用示例 二、字符串的内部表…...

HDFS 常见命令
在HDFS创建文件夹:hdfs dfs -mkdir /test 复制本地文件到HDFS中某个目录下:hdfs dfs -put /本地路径 /hdfs 路径 查看文件内容:hdfs dfs -cat /test.txt 查看当前文件夹目录:hdfs dfs -ls / 查看文件夹中的文件数:…...

示例:WPF中应用Grid的SharedSizeGroup设置整齐的布局
一、目的:应用Grid的SharedSizeGroup设置整齐的布局 二、实现 <ItemsControl ItemsSource"{local:GetStudents Count5}"><ItemsControl.ItemTemplate><DataTemplate><Grid ShowGridLines"True"><Grid.ColumnDefinit…...

React的form表单自定义校验规则
使用antd开发的过程中,必定会遇到需要对form表单进行必填校验的处理,正常情况下,我们都会一个空的必填校验,如下:一般我们只需要简单配置rules即可 <FormItem label"管理员姓名" {...itemLayout.wholeLi…...
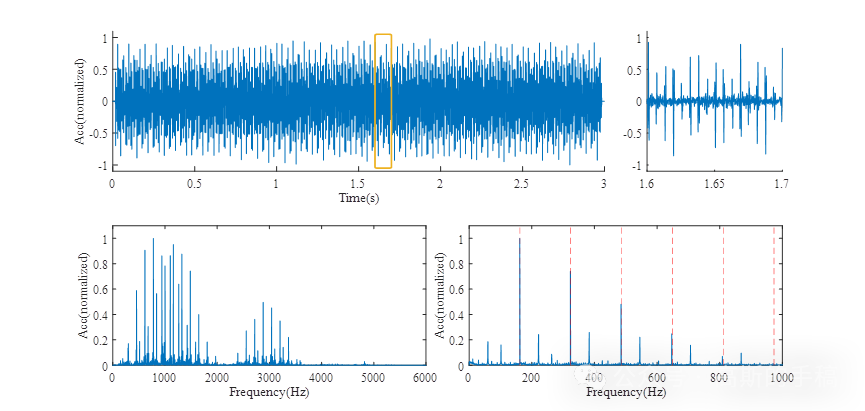
一种新的一维时间序列信号盲解卷积算法(以旋转机械故障诊断为例,MATLAB环境)
一种新的一维时间序列信号盲解卷积算法(以旋转机械故障诊断为例,MATLAB环境),可作为深度学习信号前处理过程,水个SCI不是问题。 机械设备的状态信号中往往蕴含着大量的设备异常信息。如何从繁多的机械状态信号中提取足…...
618电商是社区网站入局的好时机吗?
近日,随着618大促的临近,许多内容平台像B站、小红书等纷纷被电商活动所充斥,让用户感觉仿佛被电商绑架一般。这种用户体验的极度不佳让人开始思考,难道这就是互联网社区的未来发展方向吗? 在所有平台性质的社区中&…...

不知道密码,一样能卸载瑞星esm防病毒终端安全防护系统
离开单位后试图卸载瑞星的时候却发现还需要密码,真是烦死了。研究了几分钟后找到了完美卸载方法。 首先,让我们请出老流氓360安全卫士,下载好它,让右键菜单出现使用 360强力删除这一选项。 之后,进入安全模式&#x…...
Chromium 开发指南2024 Mac篇-安装和配置depot_tools工具(三)
1.引言 在前两篇指南中,我们详细介绍了在 macOS 环境下编译 Chromium 所需的硬件要求和系统依赖,并具体讲解了如何正确安装和配置 Xcode。通过这些步骤,您已经为编译 Chromium 打下了坚实的基础。然而,编译 Chromium 还需要配置一…...

微信小程序-路由和页面跳转API
一.wx.navigateTo wx.navigateTo是通过编程实现页面跳转,和navigator组件组件中,open-type"navigate"属性类似,是保留当前页面跳转新的页面,不适用tabbar页面。 //保留当前页面,跳转到非tabbar页面wx.navig…...
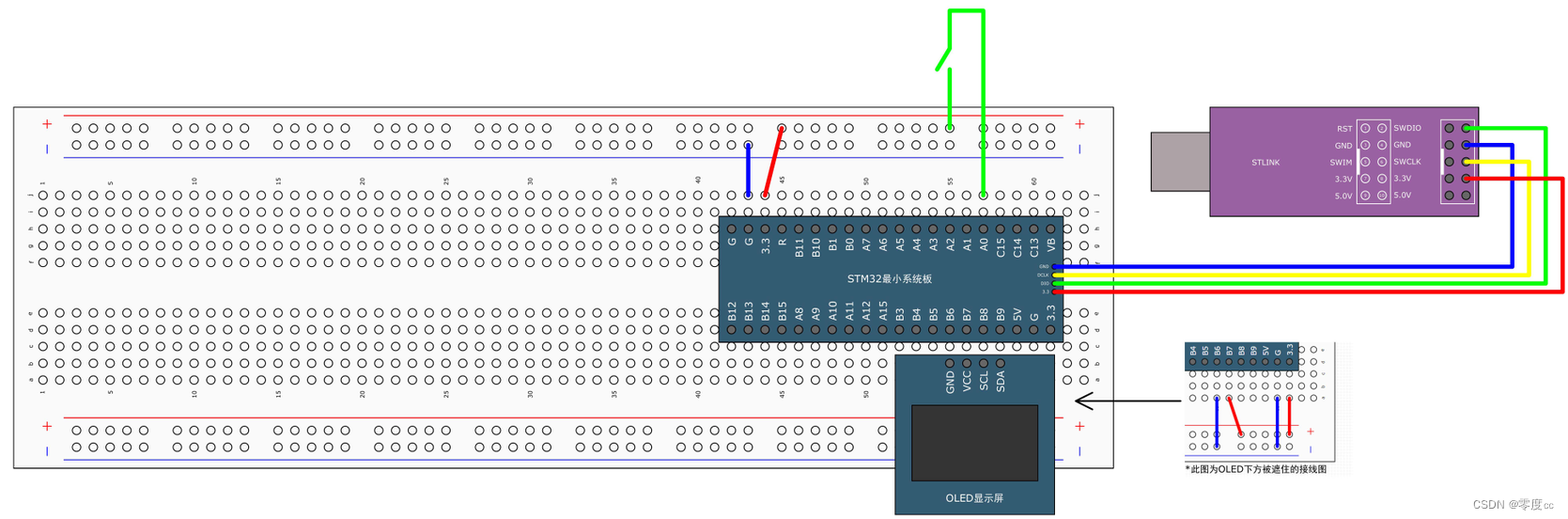
PWR电源控制
一、PWR简介 1、PWR(Power Control)电源控制 (1)PWR负责管理STM32内部的电源供电部分,可以实现可编程电压监测器和低功耗模式的功能 (2)可编程电压监测器(PVD)可以监控…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
