NumPy 双曲函数与集合操作详解
NumPy 双曲函数
NumPy 提供了 sinh()、cosh() 和 tanh() 等 ufunc,它们接受弧度值并生成相应的双曲正弦、双曲余弦和双曲正切值。
示例:
import numpy as npx = np.sinh(np.pi/2)print(x)
示例
找到数组 arr 中所有值的双曲余弦值:
import numpy as nparr = np.array([np.pi/2, np.pi/3, np.pi/4, np.pi/5])x = np.cosh(arr)print(x)
查找角度
从双曲正弦、双曲余弦、双曲正切值查找角度。例如,sinh、cosh 和 tanh 的反函数(arcsinh、arccosh、arctanh)。
NumPy 提供了 arcsinh()、arccosh() 和 arctanh() 等 ufunc,它们给出相应 sinh、cosh 和 tanh 值的弧度值。
示例
找到 1.0 的角度:
import numpy as npx = np.arcsinh(1.0)print(x)
数组中每个值的角度
示例
找到数组中所有 tanh 值的角度:
import numpy as nparr = np.array([0.1, 0.2, 0.5])x = np.arctanh(arr)print(x)
NumPy 集合操作
什么是集合
在数学中,集合是一组唯一元素的集合。
集合用于频繁进行交集、并集和差集运算。
在 NumPy 中创建集合
我们可以使用 NumPy 的 unique() 方法从任何数组中找到唯一元素。例如,创建一个集合数组,但请记住,集合数组应该只是一维数组。
示例
将以下包含重复元素的数组转换为集合:
import numpy as nparr = np.array([1, 1, 1, 2, 3, 4, 5, 5, 6, 7])x = np.unique(arr)print(x)
查找并集
要找到两个数组的唯一值,请使用 union1d() 方法。
示例
找到以下两个集合数组的并集:
import numpy as nparr1 = np.array([1, 2, 3, 4])
arr2 = np.array([3, 4, 5, 6])newarr = np.union1d(arr1, arr2)print(newarr)
查找交集
要找到仅在两个数组中都存在的值,请使用 intersect1d() 方法。
示例
找到以下两个集合数组的交集:
import numpy as nparr1 = np.array([1, 2, 3, 4])
arr2 = np.array([3, 4, 5, 6])newarr = np.intersect1d(arr1, arr2, assume_unique=True)print(newarr)
注意: intersect1d() 方法接受一个可选参数 assume_unique,如果设置为 True,则可以加快计算速度。在处理集合时应始终将其设置为 True。
查找差集
要找到第一个集合中存在但第二个集合中不存在的值,请使用 setdiff1d() 方法。
示例
找到 set2 中不存在的 set1 的差集:
import numpy as npset1 = np.array([1, 2, 3, 4])
set2 = np.array([3, 4, 5, 6])newarr = np.setdiff1d(set1, set2, assume_unique=True)print(newarr)
注意: setdiff1d() 方法接受一个可选参数 assume_unique,如果设置为 True,则可以加快计算速度。在处理集合时应始终将其设置为 True。
查找对称差
要找到两个集合中都不存在的值,请使用 setxor1d() 方法。
示例
找到 set1 和 set2 的对称差:
import numpy as npset1 = np.array([1, 2, 3, 4])
set2 = np.array([3, 4, 5, 6])newarr = np.setxor1d(set1, set2, assume_unique=True)print(newarr)
注意: setxor1d() 方法接受一个可选参数 assume_unique,如果设置为 True,则可以加快计算速度。在处理集合时应始终将其设置为 True。
最后
为了方便其他设备和平台的小伙伴观看往期文章:
微信公众号搜索:Let us Coding,关注后即可获取最新文章推送
看完如果觉得有帮助,欢迎点赞、收藏、关注
相关文章:

NumPy 双曲函数与集合操作详解
NumPy 双曲函数 NumPy 提供了 sinh()、cosh() 和 tanh() 等 ufunc,它们接受弧度值并生成相应的双曲正弦、双曲余弦和双曲正切值。 示例: import numpy as npx np.sinh(np.pi/2)print(x)示例 找到数组 arr 中所有值的双曲余弦值: import…...
)
ABSD-系统架构师(十三)
1、CDN和反向代理的基本原理都是()。 A缓存 B负载均衡 C路由转发 DNAT转发 答案:A 2、(必考)在ABSD(基于架构的软件开发)方法中,顶层被分解为()ÿ…...
PLC通过Profibus协议转Modbus协议网关接LED大屏通讯
一、背景 Modbus协议和Profibus协议是两种常用于工业控制系统的通信协议,它们在自动化领域中起着重要的作用。Modbus是一种串行通信协议,被广泛应用于各种设备之间的通信,如传感器、执行器、PLC等。而Profibus则是一种现场总线通信协议&…...
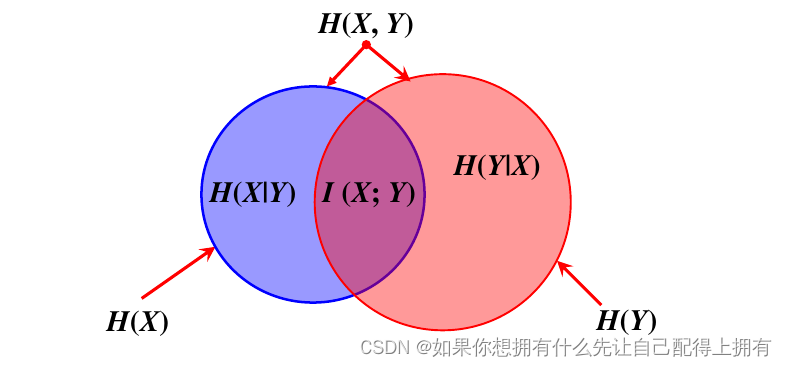
第二十三篇——香农第二定律(二):到底要不要扁平化管理?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 对于企业的理解,扁平化的管理,如果从香农第二定律…...

stm32f103 HAL库 HC-SR04测距
目录 一、实现测距二、添加TIM3控制LED根据距离以不同频率闪烁三、观察时序Modebus协议12路超声波雷达设计方案1. 系统架构设计2. 硬件设计3. 软件设计4. 通信协议设计5. 用户接口6. 安全和冗余7. 测试和验证8. 电源和物理封装9. 文档和支持 一、实现测距 配置时钟 配置定时器…...
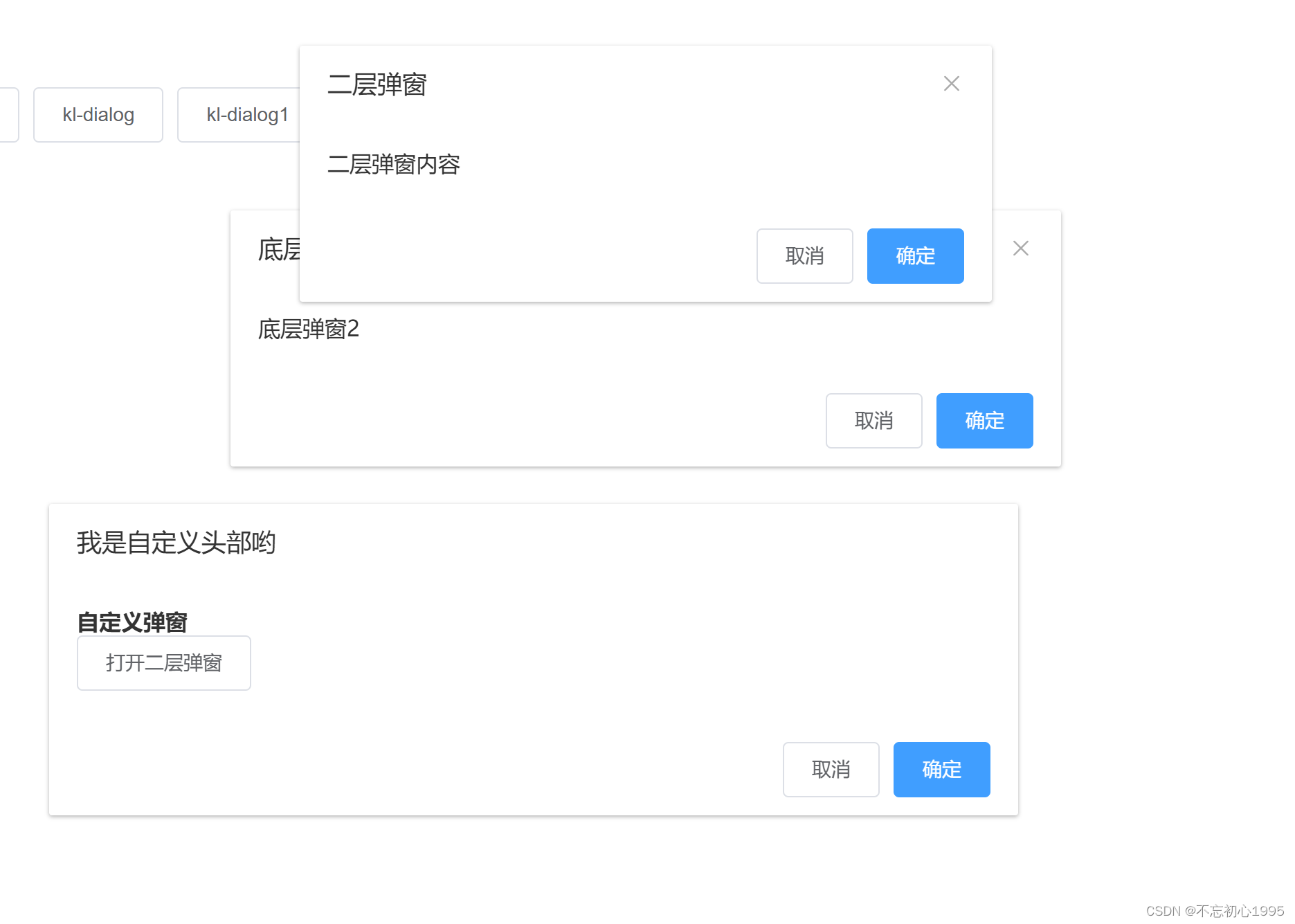
vue中通过自定义指令实现一个可拖拽,缩放的弹窗
效果 功能描述 按住头部可拖拽鼠标放到边框,可缩放多层重叠丰富的插槽,易于扩展 示例 指令代码 export const dragDialog {inserted: function (el, { value, minWidth 400, minHeight 200 }) {// 让弹窗居中let dialogHeight el.clientHeight ?…...

FreeRtos-09事件组的使用
1. 事件组的理论讲解 事件组:就是通过一个整数的bit位来代表一个事件,几个事件的or和and的结果是输出 #define configUSE_16_BIT_TICKS 0 //configUSE_16_BIT_TICKS用1表示16位,用0表示32位 1.1 事件组适用于哪些场景 某个事件若干个事件中的某个事件若干个事件中的所有事…...
多路h265监控录放开发-(1)建立head窗口并实现鼠标拖动整个窗口
头文件: //鼠标事件 用于拖动窗口//一下三个函数都是QWidget的可重载成员函数void mouseMoveEvent(QMouseEvent* ev) override;void mousePressEvent(QMouseEvent* ev) override;void mouseReleaseEvent(QMouseEvent* ev) override; 源文件: / /// 鼠标…...

ICMR 2024在普吉岛闭幕,学者与泰国舞者共舞,燃爆全场
惊艳!ICMR 2024在普吉岛闭幕,学者与泰国舞者共舞,燃爆全场! 会议之眼 快讯 ICMR(International Conference on Multimedia Retrieval)即国际多媒体检索会议,是一个专注于多媒体检索领域的顶级…...

大模型精调:实现高效迁移学习的艺术
在人工智能领域,大型预训练模型(以下简称“大模型”)已经取得了令人瞩目的成果。这些模型通过在海量数据上进行预训练,能够捕捉到丰富的特征信息,为各种下游任务提供强大的支持。然而,如何将这些大模型应用…...

epoll服务端和客户端示例代码
epoll 服务端demo #include <stdio.h> #include <sys/epoll.h> #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <arpa/inet.h> #include <fcntl.h> #include <unistd.h> #include <ne…...
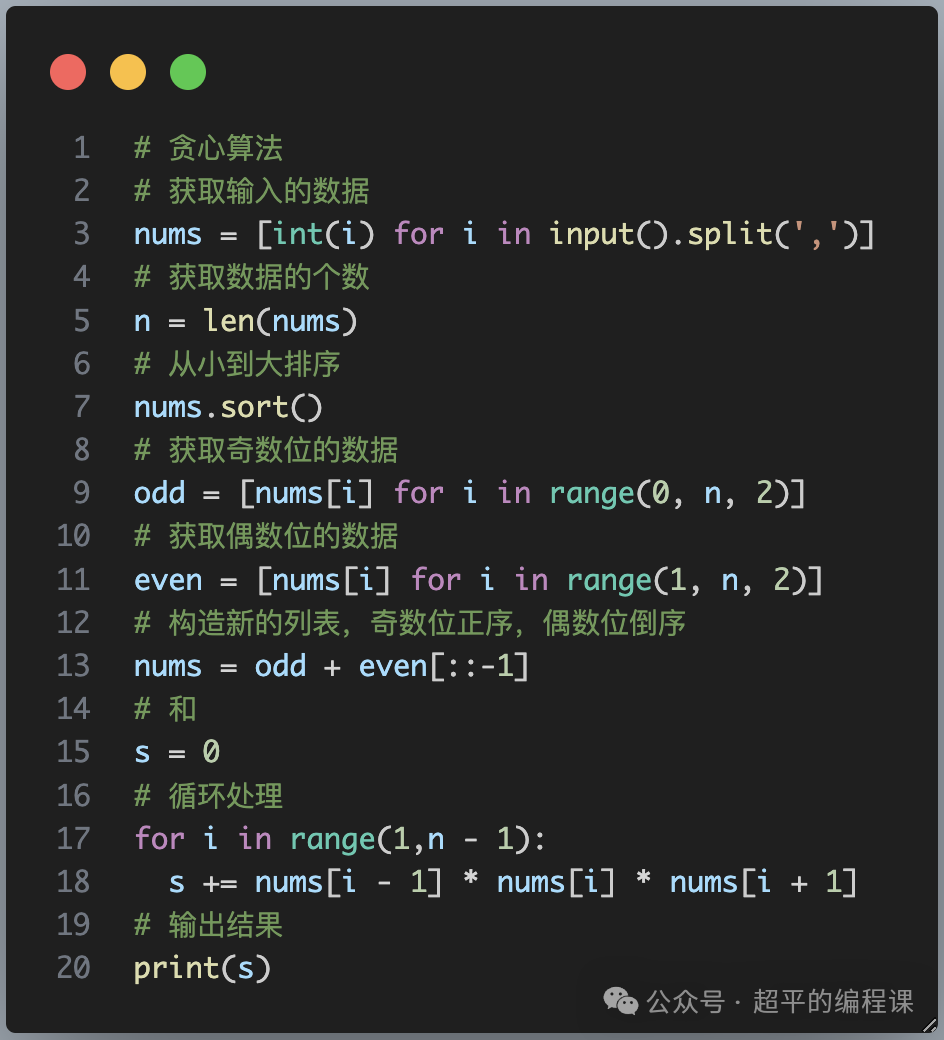
最大乘积和-第13届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第85讲。 最大乘积和&#…...

探索C嘎嘎的奇妙世界:第四关---引用与内联函数
1 引用: 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间。 #include<iostream> using namespace std;int main() {int a 0;// 引用:…...

DLS平台:惠誉全球经济展望——今年调增至2.6%,明年调减!
摘要 尽管全球货币政策逐渐转向宽松,惠誉国际评级(Fitch Ratings)在最新的《全球经济展望》中对2024年全球经济增长进行了上调。然而,由于美国经济增速放缓和其他因素的影响,2025年的全球经济增长预期则被下调。这篇文…...
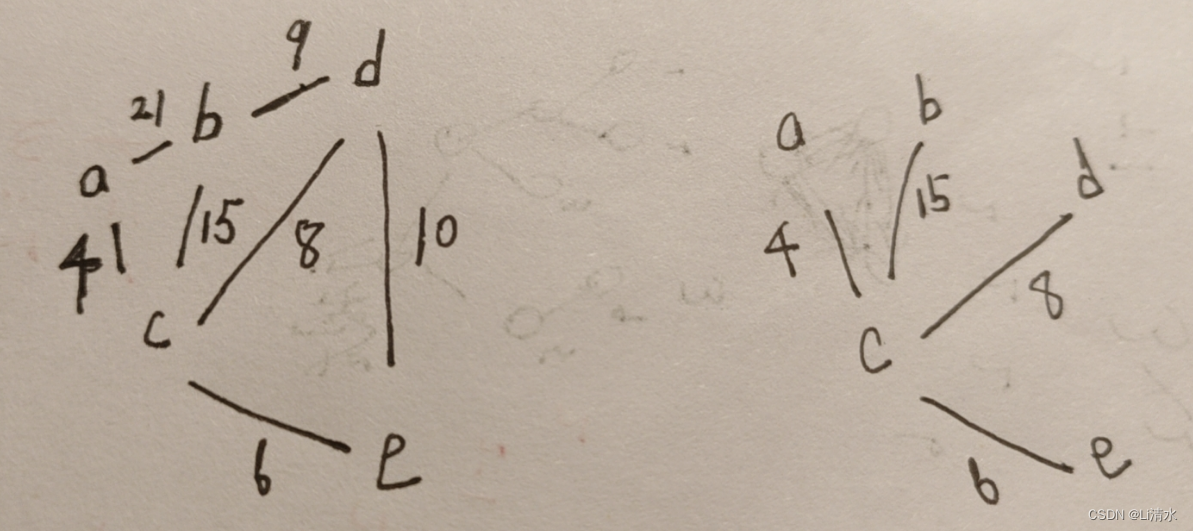
数据结构习题
第一章 绪论 与数据元素本身的形式、内容、相对位置、个数无关的是数据的 逻辑结构。 第二章 线性表 在一个有127个元素的顺序表中插入一个新元素并保持原来顺序不变,平均要移动的元素个数为 63.5。 n/2 单链表的存储密度 小于1。 创建一个包括n个结点的有序单链…...

交通银行软件开发工程师校招面试经历
本文介绍2024届春招中,交通银行总行的软件开发工程师岗位1场面试的基本情况、提问问题等。 2024年04月投递了交通银行总行的软件开发工程师岗位,暂时不清楚所在部门。目前完成了一面,并进入体检阶段;在这里记录一下面试的相关经历…...

bashrc和profile区别
作用与目的: .bashrc:这个文件主要用于配置和自定义用户的终端环境和行为。每次启动新的终端时,.bashrc文件都会被执行,加载用户设置的环境变量、别名、函数等。这使得用户能够根据自己的喜好和需求来定制终端的行为和外观。profi…...

BC153 [NOIP2010]数字统计
数字统计 一.题目描述二.输入描述:三.输出描述:四.数字范围五.题目思路六.代码实现 一.题目描述 请统计某个给定范围[L, R]的所有整数中,数字2出现的次数。 比如给定范围[2, 22],数字2在数2中出现了1次,在数12中出现1次…...

浅谈LavelDB
简介 LevelDB 是一个开源的轻量级键值存储库,由 Google 开发,用于提供快速的键值存储和支持读写大量数据。LevelDB 具有高性能、快速的读取和写入速度以及支持原子操作的特点,适合用于需要高效存储和检索键值数据的场景。 LevelDB 主要特点…...

Google Earth Engine(GEE)——NDVI的时间序列分析和在线出图
函数: ui.Chart.array.values(array, axis, xLabels) Generates a Chart from an array. Plots separate series for each 1-D vector along the given axis. - X-axis = Array index along axis, optionally labeled by xLabels. - Y-axis = Value. - Series = Vector, d…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
