当前位置： 首页 > news >正文

机器学习课程复习——逻辑回归

news 2026/2/11 6:36:45

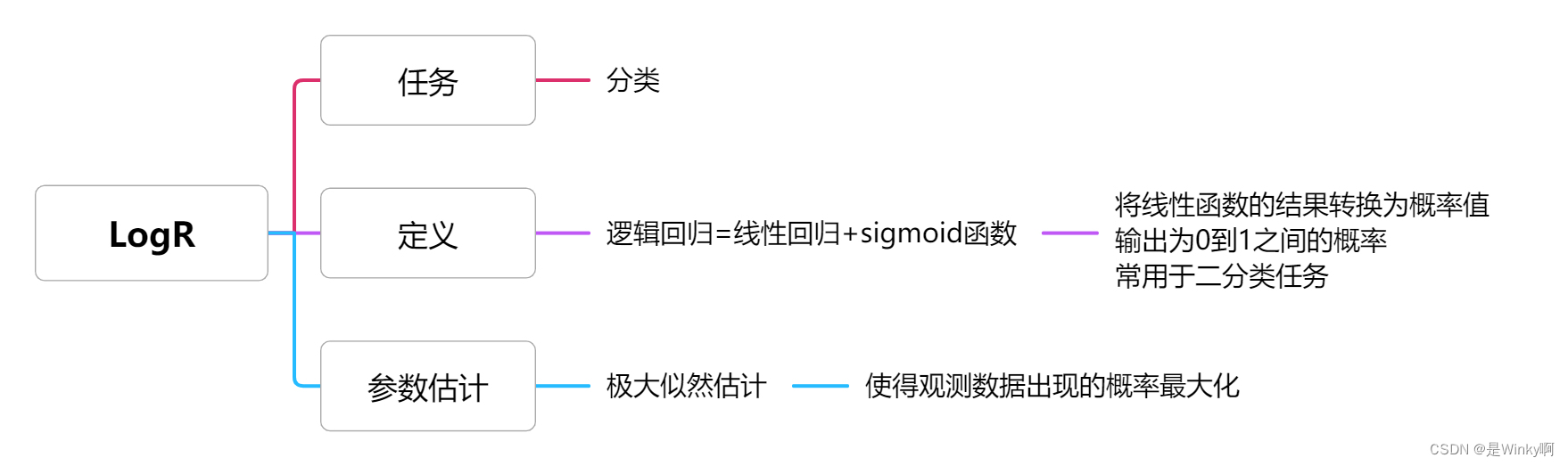
 1. 激活函数

Q：激活函数有哪些？

SigmoidS型函数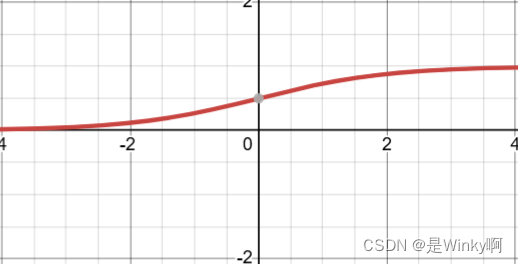\frac{1}{1+e^{-x}}
Tanh 双曲正切函数

相关文章：

机器学习课程复习——逻辑回归

1. 激活函数 Q：激活函数有哪些？ SigmoidS型函数Tanh 双曲正切函数...

编程日记 2024/6/19 10:12:50

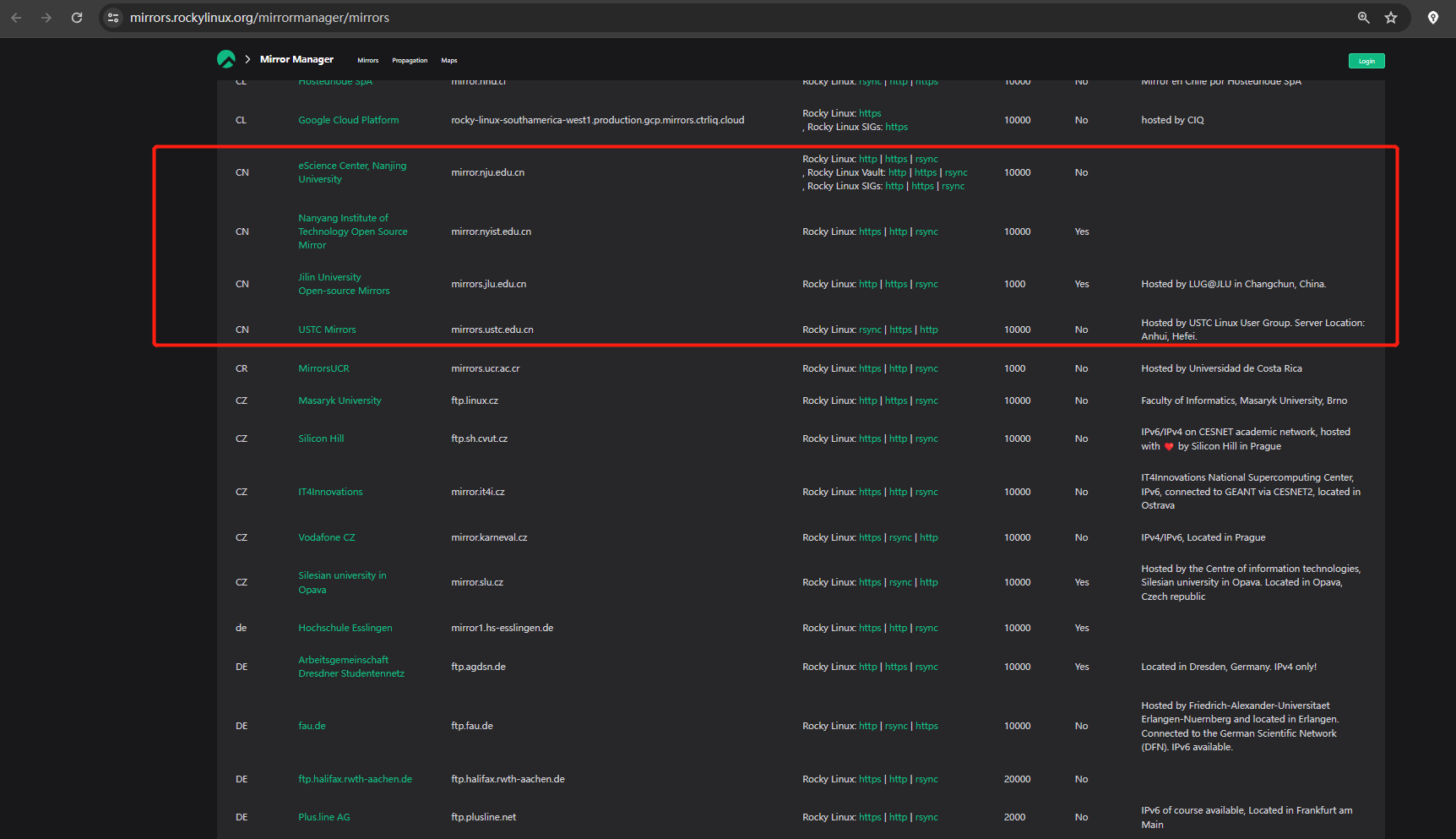
Rocky Linux 更换CN镜像地址

官方镜像列表&#xff0c;下拉查找 官方镜像列表&#xff1a;https://mirrors.rockylinux.org/mirrormanager/mirrorsCN 开头的站点。 一键更改镜像地址脚本 以下是更改从默认更改到阿里云地址 cat <<EOF>>/RackyLinux_Update_repo.sh #!/bin/bash # -*- codin…...

编程日记 2024/6/19 10:11:48

Linux rm命令由于要删的文件太多报-bash: /usr/bin/rm:参数列表过长，无法删除的解决办法

银河麒麟系统&#xff0c;在使用rm命令删除文件时报了如下错误&#xff0c;删不掉&#xff1a; 查了一下&#xff0c;原因就是要删除的文件太多了&#xff0c;例如我当前要删的文件共有这么多&#xff1a; 查到了解决办法&#xff0c;记录在此。需要使用xargs命令来解决参数列表…...

编程日记 2024/6/19 10:05:41

【包管理】Node.JS与Ptyhon安装

文章目录 Node.JSPtyhon Node.JS Node.js的安装通常包括以下几个步骤&#xff1a; 访问Node.js官网&#xff1a; 打开Node.js的官方网站&#xff08;如&#xff1a;https://nodejs.org/zh-cn/download/&#xff09;。 下载安装包&#xff1a; 根据你的操作系统选择对应的Node…...

编程日记 2024/6/19 10:04:38

SpringMVC系列四: Rest-优雅的url请求风格

Rest请求 &#x1f49e;Rest基本介绍&#x1f49e;Rest风格的url-完成增删改查需求说明代码实现HiddenHttpMethodFilter机制注意事项和细节 &#x1f49e;课后作业 上一讲, 我们学习的是SpringMVC系列三: Postman(接口测试工具) 现在打开springmvc项目 &#x1f49e;Rest基本介…...

编程日记 2024/6/19 10:03:36

Hexo 搭建个人博客（ubuntu20.04）

1 安装 Nodejs 和 npm 首先登录NodeSource官网&#xff1a; Nodesource Node.js DEB 按照提示安装最新的 Node.js 及其配套版本的 npm。 &#xff08;1&#xff09;以 sudo 用户身份运行下面的命令&#xff0c;下载并执行 NodeSource 安装脚本&#xff1a; sudo curl -fsSL…...

编程日记 2024/6/19 10:02:34

【论文阅读】-- Attribute-Aware RBFs：使用 RT Core 范围查询交互式可视化时间序列颗粒体积

Attribute-Aware RBFs: Interactive Visualization of Time Series Particle Volumes Using RT Core Range Queries 摘要1 引言2 相关工作2.1 粒子体渲染2.2 RT核心方法 3 渲染彩色时间序列粒子体积3.1 场重构3.1.1 密度场 Φ3.1.2 属性字段 θ3.1.3 优化场重建 3.2 树结构构建…...

编程日记 2024/6/19 10:00:31

A类IP介绍

1&#xff09;A类ip给谁用&#xff1a; 给广域网用&#xff0c;公网ip使用A类地址&#xff0c;作为公网ip时&#xff0c;Ip地址是全球唯一的。 2&#xff09;基本介绍 ip地址范围 - 理论范围 0.0.0.0 ~127.255.255.255&#xff1a;00000000 00000000 00000000 00000000 ~ 0111…...

编程日记 2024/6/19 9:59:29

HTML5基本语法

文章目录 HTML5基本语法一、基础标签1、分级标题2、段标签3、换行及水平线标签4、文本格式标签 二、图片标签1、格式2、属性介绍 三、音频标签1、格式2、属性介绍 四、视频标签1、格式2、属性介绍 五、链接标签1、格式2、显示特点3、属性介绍4、补充&#xff08;空链接&#xf…...

编程日记 2024/6/19 9:57:26

正则表达式常用表示

视频教程&#xff1a;10分钟快速掌握正则表达式 正则表达式在线测试工具&#xff08;亲测好用&#xff09;&#xff1a;测试工具 正则表达式常用表示 限定符 a*&#xff1a;a出现0次或多次a&#xff1a;a出现1次或多次a?&#xff1a;a出现0次或1次a{6}&#xff1a;a出现6次a…...

编程日记 2024/6/19 9:56:25

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程 一、编译后目录列表二、make distclean三、生成.config文件：make V=1 ARCH=arm64 CROSS_COMPILE=aarch64-linux-gnu- evb-rk3568_defconfig四、开始编译：CROSS_COMPILE=aarch64-…...

编程日记 2024/6/19 9:55:22

11.1 Go 标准库的组成

&#x1f49d;&#x1f49d;&#x1f49d;欢迎莅临我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

编程日记 2024/6/19 9:54:19

【UG\NX二次开发】UF 调用Grip例子（实现Grip调用目标dll）(UF_call_grip)

此例子是对&#xff1a;【UG\NX二次开发】UF 加载调用与卸载目标dll(UF_load_library、UF_unload_library)_ug二次开发dll自动加载-CSDN博客的补充。 ①创建txt文本&#xff0c;编写以下内容(功能&#xff1a;接收路径&#xff0c;调用该路径的dll)。改后缀为Grip文件(.grs)。…...

编程日记 2024/6/19 9:48:13

[算法刷题积累] 两数之和以及进阶引用

两数之和很经典&#xff0c;通常对于首先想到的就是暴力的求解&#xff0c;当然这没有问题&#xff0c;但是我们如果想要追求更优秀算法&#xff0c;就需要去实现更加简便的复杂度。 这里就要提到我们的哈希表法: 我们可以使用unordered_map去实现&#xff0c;也可以根据题目&a…...

编程日记 2024/6/19 9:47:11

pytest+parametrize+yaml实例

# 一、yaml格式 # # yaml是一种数据类型&#xff0c;可以和json之间灵活的切换&#xff0c;支持注释、换行、字符串等。可以用于配置文件或编写测试用例。 # # 数据结构&#xff1a;一般是键值对的方式出现。注意编写时值前面必须有空格&#xff0c;键&#xff1a;&#xff08;…...

编程日记 2024/6/19 9:43:06

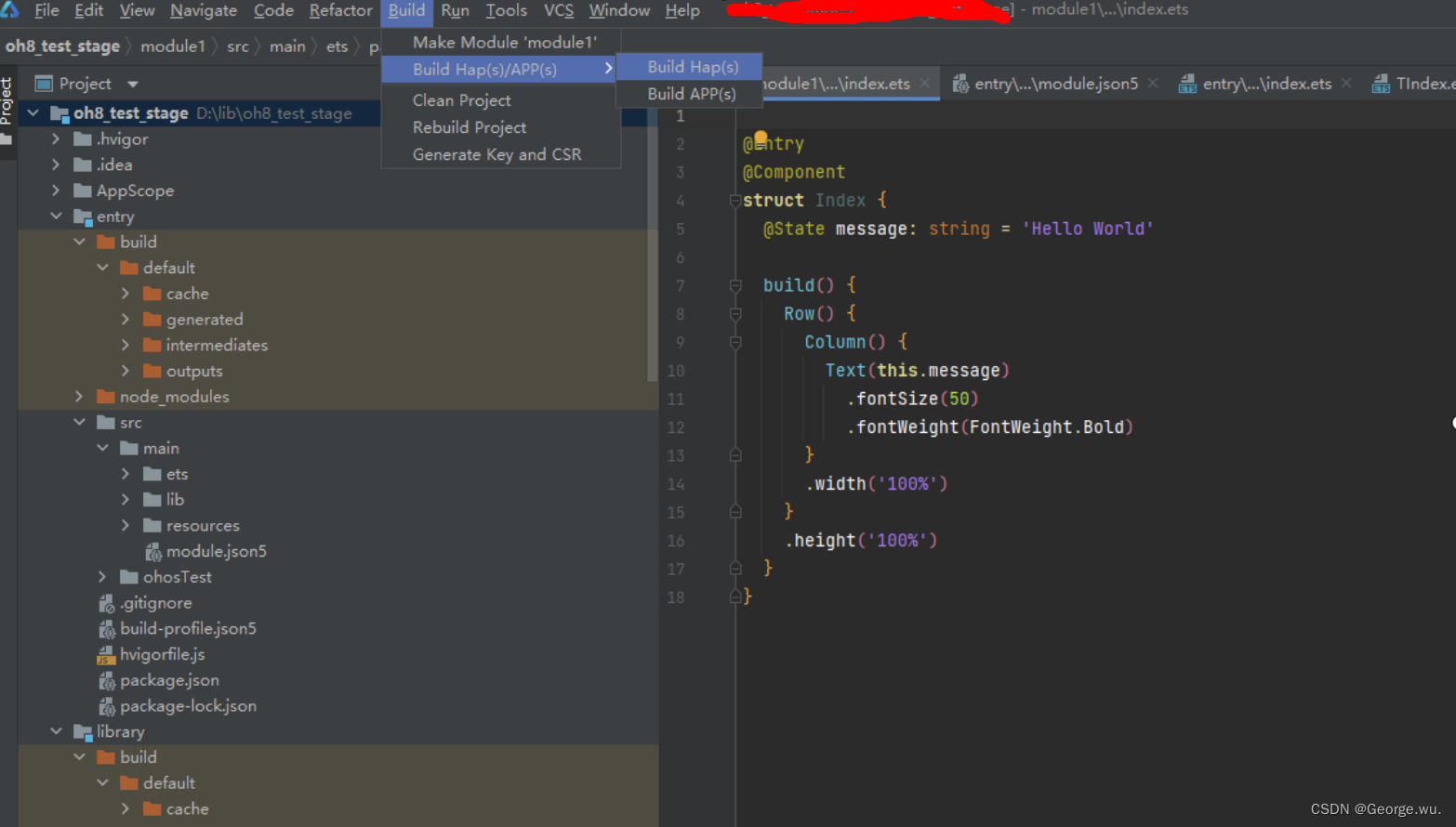
【HarmonyOS】鸿蒙应用模块化实现

【HarmonyOS】鸿蒙应用模块化实现 一、Module的概念 Module是HarmonyOS应用的基本功能单元&#xff0c;包含了源代码、资源文件、第三方库及应用清单文件&#xff0c;每一个Module都可以独立进行编译和运行。一个HarmonyOS应用通常会包含一个或多个Module&#xff0c;因此&am…...

编程日记 2024/6/19 9:42:04

深入Node.js：实现网易云音乐数据自动化抓取

随着互联网技术的飞速发展&#xff0c;数据已成为企业和个人获取信息、洞察市场趋势的重要资源。音频数据&#xff0c;尤其是来自流行音乐平台如网易云音乐的数据&#xff0c;因其丰富的用户交互和内容多样性&#xff0c;成为研究用户行为和市场动态的宝贵资料。本文将深入探讨…...

编程日记 2024/6/19 9:38:57

【Docker实战】jenkins卡在编译Dockerfile的问题

我们的项目是标准的CI/CD流程&#xff0c;也即是GitlabJenkinsHarborDocker的容器自动化部署。 经历了上上周的docker灾难&#xff0c;上周的服务器磁盘空间灾难&#xff0c;这次又发生了jenkins卡住的灾难。 当然&#xff0c;这些灾难有一定的连锁反应&#xff0c;是先发生的d…...

编程日记 2024/6/19 9:37:55

rust 多线程分发数据

use std::sync::{Arc, Mutex}; use std::collections::VecDeque; use std::thread::{self, sleep}; use rand::Rng; use std::time::Duration;fn main() {let list: Arc<Mutex<VecDeque<String>>> Arc::new(Mutex::new(VecDeque::new()));// 创建修改线程le…...

编程日记 2024/6/19 9:36:51

CentOS 7x 使用Docker 安装oracle11g完整方法

1.安装docker-ce 安装依赖的软件包 yum install -y yum-utils device-mapper-persistent-data lvm2添加Docker的阿里云yum源 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo更新软件包索引 yum makecache fast查看docker…...

编程日记 2024/6/19 9:35:47

华为云AI开发平台ModelArts

华为云ModelArts&#xff1a;重塑AI开发流程的“智能引擎”与“创新加速器”&#xff01; 在人工智能浪潮席卷全球的2025年&#xff0c;企业拥抱AI的意愿空前高涨&#xff0c;但技术门槛高、流程复杂、资源投入巨大的现实&#xff0c;却让许多创新构想止步于实验室。数据科学家…...

编程新知 2026/2/10 23:05:30

19c补丁后oracle属主变化，导致不能识别磁盘组

补丁后服务器重启&#xff0c;数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后&#xff0c;存在与用户组权限相关的问题。具体表现为&#xff0c;Oracle 实例的运行用户&#xff08;oracle&#xff09;和集…...

编程新知 2026/2/8 4:37:10

【网络】每天掌握一个Linux命令 - iftop

在Linux系统中&#xff0c;iftop是网络管理的得力助手&#xff0c;能实时监控网络流量、连接情况等&#xff0c;帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

编程新知 2025/10/10 17:03:53

C++_核心编程_多态案例二-制作饮品

#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为&#xff1a;煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例&#xff0c;提供抽象制作饮品基类&#xff0c;提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

编程新知 2026/2/8 20:42:55

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank&#xff1f;由于时间太久&#xff0c;我真忘记了。搜搜发现&#xff0c;还真有人和我一样。见下面的链接&#xff1a;https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2026/2/8 20:41:51

基于FPGA的PID算法学习———实现PID比例控制算法

基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容&#xff1a;参考网站&#xff1a; PID算法控制 PID即&#xff1a;Proportional&#xff08;比例&#xff09;、Integral&#xff08;积分&…...

编程新知 2026/2/8 18:25:56

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

《Playwright：微软的自动化测试工具详解》

Playwright 简介:声明内容来自网络&#xff0c;将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具&#xff0c;支持 Chrome、Firefox、Safari 等主流浏览器&#xff0c;提供多语言 API&#xff08;Python、JavaScript、Java、.NET&#xff09;。它的特点包括&a…...

编程新知 2025/7/23 15:00:00

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】

大家好&#xff0c;我是java1234_小锋老师&#xff0c;看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】&#xff0c;分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

编程新知 2026/1/29 5:39:49