LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】
LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】
- 题目描述:
- 解题思路一:滑动窗口与排序
- 解题思路二:0
- 解题思路三:0
题目描述:
给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。
在一步操作中,你可以执行下述指令:
在范围 [0, nums.length - 1] 中选择一个 此前没有选过 的下标 i 。
将 nums[i] 替换为范围 [nums[i] - k, nums[i] + k] 内的任一整数。
数组的 美丽值 定义为数组中由相等元素组成的最长子序列的长度。
对数组 nums 执行上述操作任意次后,返回数组可能取得的 最大 美丽值。
注意:你 只 能对每个下标执行 一次 此操作。
数组的 子序列 定义是:经由原数组删除一些元素(也可能不删除)得到的一个新数组,且在此过程中剩余元素的顺序不发生改变。
示例 1:
输入:nums = [4,6,1,2], k = 2
输出:3
解释:在这个示例中,我们执行下述操作:
- 选择下标 1 ,将其替换为 4(从范围 [4,8] 中选出),此时 nums = [4,4,1,2] 。
- 选择下标 3 ,将其替换为 4(从范围 [0,4] 中选出),此时 nums = [4,4,1,4] 。
执行上述操作后,数组的美丽值是 3(子序列由下标 0 、1 、3 对应的元素组成)。
可以证明 3 是我们可以得到的由相等元素组成的最长子序列长度。
示例 2:
输入:nums = [1,1,1,1], k = 10
输出:4
解释:在这个示例中,我们无需执行任何操作。
数组 nums 的美丽值是 4(整个数组)。
提示:
1 <= nums.length <= 105
0 <= nums[i], k <= 105
解题思路一:滑动窗口与排序
将每个数x变为一个区间[x-k,x+k],然后排序,判断区间是否有交集:也就是说,要满足
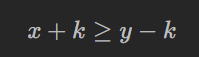
也就是: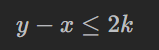
class Solution {public int maximumBeauty(int[] nums, int k) {Arrays.sort(nums);int ans = 0;int left = 0;for (int right = 0; right < nums.length; right++) {while (nums[right] - nums[left] > 2 * k) {left++;}ans = Math.max(ans, right - left + 1);}return ans;}
}
时间复杂度:O(nlogn)
空间复杂度:O(1)
解题思路二:0
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠
相关文章:

LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】
LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】 题目描述:解题思路一:滑动窗口与排序解题思路二:0解题思路三:0 题目描述: 给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。 在一步操…...

RIP与OSPF发布默认路由(华为)
#交换设备 RIP与OSPF发布默认路由 合理使用默认路由可以很大程度上减少本地路由表的大小,并可以较好的隐藏一个网络中的路由信息,保护自身网络的隐秘性 另外如果在同一个路由器两端使用了不同的路由协议,那么如果不做路由引入或者发布默认…...

Android 一个改善的okHttp封装库
Android Studio 使用前,对于Android Studio的用户,可以选择添加: compile project(‘:okhttputils’) 或者 compile ‘com.zhy:okhttputils:2.0.0’ Eclipse 自行copy源码。 二、基本用法 目前基本的用法格式为: OkHttpUtils .get()…...
瓦罗兰特低价区怎么下载 瓦罗兰特低价区下载教程+免费加速器推荐
瓦罗兰特是由拳头发行的游戏,以其丰富的游戏内容和刺激的竞技体验赢得了广大玩家的喜爱。于其它热门的射击游戏不一样的是,我们在游戏中可以选择不的英雄,每一个英雄都有着自己独特的技能,我们还可以在游戏中强行改变地形帮助我们…...

lspci总结
lspci总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨一个在 Linux 系统中常用的命令:lspci。lspci 命令用于列出当前系统中的 P…...

Android开启HTTP服务
需求:通过手机给设备升级固件,设备有WIFI 方案:升级包放到APP可以访问的目录,手机开热点并启动一个HTTP服务,设备连接手机热点,另外,设备端开启一个 telnet 服务,手机通过 telnet 登…...

NLP - word2vec详解
Word2Vec是一种用于将词汇映射到高维向量空间的自然语言处理技术。由Google在2013年提出,它利用浅层神经网络模型来学习词汇的分布式表示。Word2Vec有两种主要模型:CBOW(Continuous Bag of Words)和Skip-gram。 1. 模型介绍 Con…...

AI办公自动化:用通义千问批量翻译长篇英语TXT文档
在deepseek中输入提示词: 你是一个Python编程专家,现在要完成一个编写基于qwen-turbo模型API和dashscope库的程序脚本,具体步骤如下: 打开文件夹:F:\AI自媒体内容\待翻译; 获取里面所有TXT文档ÿ…...

一键解压,无限可能——BetterZip,您的Mac必备神器!
BetterZip for Mac 是一款高效、智能且安全的解压缩软件,专为Mac用户设计。它提供了直观易用的界面,使用户能够轻松应对各种压缩和解压缩需求。 这款软件不仅支持多种压缩格式,如ZIP、RAR、7Z等,还具备快速解压和压缩文件的能力。…...

【数学】什么是最大似然估计?如何求解最大似然估计
背景 最大似然估计(Maximum Likelihood Estimation, MLE)是一种估计统计模型参数的方法。它在众多统计学领域中被广泛使用,比如回归分析、时间序列分析、机器学习和经济学。其核心思想是:给定一个观测数据集,找到一组…...

跟张良均老师学大数据人工智能|企业项目试岗实训开营
我国高校毕业生数量连年快速增长,从2021年的909万人到2022年的1076万人,再到2023年的1158万人,预计到2024年将达到1187万人,2024年高校毕业生数量再创新高。 当年高校毕业生人数不等于进入劳动力市场的高校毕业生人数&#x…...

Pentest Muse:一款专为网络安全人员设计的AI助手
关于Pentest Muse Pentest Muse是一款专为网络安全研究人员和渗透测试人员设计和开发的人工智能AI助手,该工具可以帮助渗透测试人员进行头脑风暴、编写Payload、分析代码或执行网络侦查任务。除此之外,Pentest Muse甚至还能够执行命令行代码并以迭代方式…...
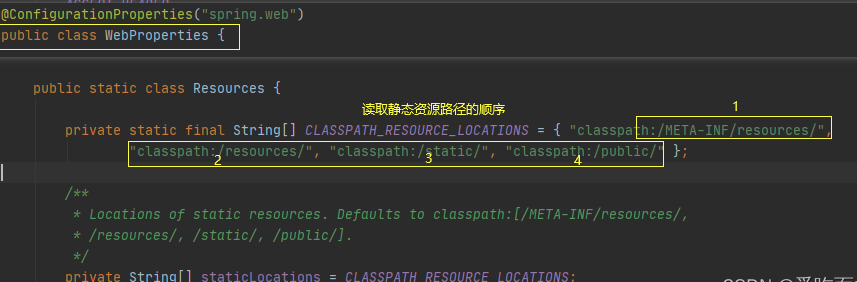
10 SpringBoot 静态资源访问
我们在开发Web项目的时候,往往会有很多静态资源,如html、图片、css等。那如何向前端返回静态资源呢? 以前做过web开发的同学应该知道,我们以前创建的web工程下面会有一个webapp的目录,我们只要把静态资源放在该目录下…...
Unity 之通过自定义协议从浏览器启动本地应用程序
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity 之通过自定义协议从浏览器启动本地应用程序 TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进…...
Python抓取天气信息
Python的详细学习还是需要些时间的。如果有其他语言经验的,可以暂时跟着我来写一个简单的例子。 2024年最新python教程全套,学完即可进大厂!(附全套视频 下载) (qq.com) 我们计划抓取的数据:杭州的天气信息…...
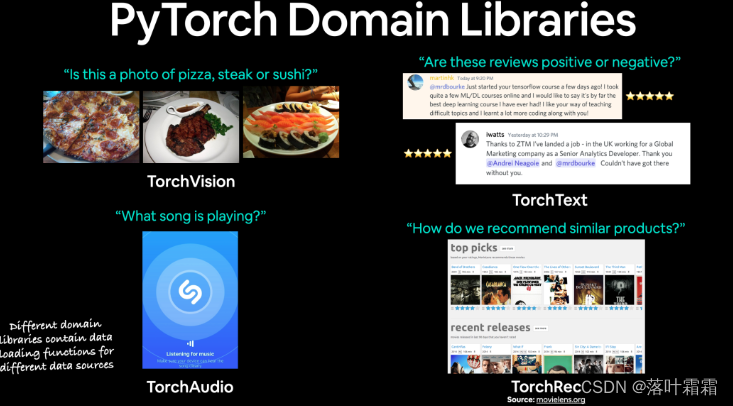
【超越拟合:深度学习中的过拟合与欠拟合应对策略】
如何处理过拟合 由于过拟合的主要问题是你的模型与训练数据拟合得太好,因此你需要使用技术来“控制它”。防止过拟合的常用技术称为正则化。我喜欢将其视为“使我们的模型更加规则”,例如能够拟合更多类型的数据。 让我们讨论一些防止过拟合的方法。 获…...

【Orange Pi 5与Linux内核编程】-理解Linux内核中的container_of宏
理解Linux内核中的container_of宏 文章目录 理解Linux内核中的container_of宏1、了解C语言中的struct内存表示2、Linux内核的container_of宏实现理解3、Linux内核的container_of使用 Linux 内核包含一个名为 container_of 的非常有用的宏。本文介绍了解 Linux 内核中的 contain…...

003.Linux SSH协议工具
我 的 个 人 主 页:👉👉 失心疯的个人主页 👈👈 入 门 教 程 推 荐 :👉👉 Python零基础入门教程合集 👈👈 虚 拟 环 境 搭 建 :👉&…...

web前端组织分析:深入剖析其结构、功能与未来趋势
web前端组织分析:深入剖析其结构、功能与未来趋势 在数字化浪潮的推动下,Web前端组织作为连接用户与数字世界的桥梁,其重要性日益凸显。本文将从四个方面、五个方面、六个方面和七个方面对Web前端组织进行深入分析,揭示其结构特点…...
GitCode热门开源项目推荐:Spider网络爬虫框架
在数字化高速发展时代,数据已成为企业决策和个人研究的重要资源。网络爬虫作为一种强大的数据采集工具受到了广泛的关注和应用。在GitCode这一优秀的开源平台上,Spider网络爬虫框架凭借其简洁、高效和易用性,成为了众多开发者的首选。 一、系…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
