代码随想录算法训练营第六十四天 | 图论理论基础、深搜理论基础、广搜理论基础、98. 所有可达路径
图论理论基础
我写在了个人语雀笔记中
https://www.yuque.com/yuqueyonghu8mml9e/bmbl71/ex473q4y0ebs0l3r?singleDoc#
深搜理论基础
https://www.yuque.com/yuqueyonghu8mml9e/bmbl71/zamfikz08c2haptn?singleDoc#
98. 所有可达路径
题目链接:98. 所有可达路径
文字讲解:98. 所有可达路径 | 代码随想录
解题思路
邻接矩阵
1.确认递归函数和参数
首先dfs函数中,一定要有一个图,其次是我们当前遍历的节点,为x
其次还需要一个n,来表示终点,当x==n时则表示达到了终点
最后就是需要保存单一路径的path,和结果result了
2.确定终止条件
当我们的x==n时,则我们找到了从出发点到结束点的路径
3.处理目前搜索节点的路径
首先我们是要找到x节点指向了哪些节点?
for(int i = 1 ; i<=n ; i++)
{if(graph[x][i]==1){//找到x指向的节点,就是节点i//此时我们要将x指向的节点加入到path中path.push_back(i);//进入下一层递归dfs(graph,i,n);//回溯的过程path.pop_back(); }
}
4.打印结果
// 输出结果
if (result.size() == 0) cout << -1 << endl;
for (const vector<int> &pa : result) {for (int i = 0; i < pa.size() - 1; i++) { // 这里指打印到倒数第二个cout << pa[i] << " ";}cout << pa[pa.size() - 1] << endl; // 这里再打印倒数第一个,控制最后一个元素后面没有空格
}完整代码:
#include<bits/stdc++.h>
using namespace std;
vector<int> path;
vector<vector<int>> result;
void dfs(const vector<vector<int>>& graph , int x, int n)
{if(x==n){result.push_back(path);return;}for(int i = 1 ; i <=n ; i++){if(graph[x][i]==1){path.push_back(i);dfs(graph,i,n);path.pop_back();}}
}int main()
{int n,m,s,t;cin>> n >> m;//构造图vector<vector<int>> graph(n+1,vector<int>(n+1,0));while(m--){cin>>s>>t;graph[s][t] =1;}//开始搜索,因为是从节点1出发,因此先加入节点1path.push_back(1);dfs(graph,1,n);if(result.size() == 0) cout<< -1 << endl;for(const vector<int>& pa : result) //取结果中每一个路径{for(int i = 0; i < pa.size()-1 ; i++){cout<< pa[i] << " "; }cout << pa[pa.size()-1] << endl; //最后一个元素单独打印}return 0;
}邻接表(构造和遍历方式有所不同)
#include<bits/stdc++.h>
using namespace std;
vector<int> path;
vector<vector<int>> result;
void dfs(const vector<list<int>>& graph , int x, int n)
{if(x==n){result.push_back(path);return;}for(int i : graph[x]) //这里是和邻接矩阵不同的地方,遍历方式{path.push_back(i);dfs(graph,i,n);path.pop_back();}
}int main()
{int n,m,s,t;cin>> n >> m;//构造图vector< list<int> > graph(n+1);while(m--){cin>>s>>t;graph[s].push_back(t); //下标对应节点}//开始搜索,因为是从节点1出发,因此先加入节点1path.push_back(1);dfs(graph,1,n);if(result.size() == 0) cout<< -1 << endl;for(const vector<int>& pa : result) //取结果中每一个路径{for(int i = 0; i < pa.size()-1 ; i++){cout<< pa[i] << " "; }cout << pa[pa.size()-1] << endl; //最后一个元素单独打印}return 0;
}广搜理论基础
广搜理论基础
相关文章:

代码随想录算法训练营第六十四天 | 图论理论基础、深搜理论基础、广搜理论基础、98. 所有可达路径
图论理论基础 我写在了个人语雀笔记中 https://www.yuque.com/yuqueyonghu8mml9e/bmbl71/ex473q4y0ebs0l3r?singleDoc# 深搜理论基础 https://www.yuque.com/yuqueyonghu8mml9e/bmbl71/zamfikz08c2haptn?singleDoc# 98. 所有可达路径 题目链接:98. 所有可达…...

【教师资格证考试综合素质——法律专项】教师法笔记以及练习题
《中华人民共和国教师法》 一.首次颁布:第一部《中华人民共和国教师法》于1993年10月31日由第八届全国人民代表大会常务委员会第四次会议通过,1994年1月1日起执行。 二.历次修改:2009年8月27日第十一届全国人民代表…...
图卷积网络(Graph Convolutional Network, GCN)
图卷积网络(Graph Convolutional Network, GCN)是一种用于处理图结构数据的深度学习模型。GCN编码器的核心思想是通过邻接节点的信息聚合来更新节点表示。 图的表示 一个图 G通常表示为 G(V,E),其中: V 是节点集合,…...
】pipeline 实际调用的是什么? __call__ 方法!)
【diffusers 极速入门(一)】pipeline 实际调用的是什么? __call__ 方法!
在使用 diffusers 库进行图像生成时,你可能会发现管道(pipeline)对象可以像函数一样被调用。这背后的魔法是什么呢?答案是:__call__ 方法!本文将通过简单的案例代码,带你快速了解 diffusers 管道…...

【DPDK学习路径】二、DPDK简介
DPDK(Data Plane Development Kit)是一个框架,用于快速报文处理。 在linux内核提供的报文处理模型中,接收报文的处理路径为:首先由网卡硬件接收,产生硬中断,触发网卡驱动程序注册的中断函数处理,之后产生软…...
python基础 002 - 2 常用数据类型
python的常用数据类型 int , 整型 1,2,3float ,小数,浮点类型1.2bool , boolean 布尔,真假。判断命题。True Flasestr ,字符串 list , 列表 a []tuple, 元组 a ()dict , dictionary, 字典 a {}set , 集合 a {} 1 查看数据类型 typ…...

爆赞!GitHub首本Python开发实战背记手册,标星果然百万名不虚传
Python (发音:[ paiθ(ə) n; (US) paiθɔn ] n. 蟒蛇,巨蛇 ),是一种面向对象的解释性的计算机程序设计语言,也是一种功能强大而完善的通用型语言,已经具有十多年的发展历史,成熟且稳定。Python 具有脚本语言中最丰富…...

Spring源码-xxxAware实现类和BeanPostProcessor接口调用过程
xxxAware实现类作用 以ApplicationContextAware接口为例 ApplicationContextAware的作用是可以方便获取Spring容器ApplicationContext,从而可以获取容器内的Bean package org.springframework.context;import org.springframework.beans.BeansException; import or…...

Uni-app x
uni-app x,是下一代 uni-app,是一个跨平台应用开发引擎。 uni-app x 是一个庞大的工程,它包括uts语言、uvue渲染引擎、uni的组件和API、以及扩展机制。 uts是一门类ts的、跨平台的、新语言。uts在iOS端编译为swift、在Android端编译为kotli…...

Python 基础:文件
目录 一、从文件中读取数据1.1 读取整个文件1.2 逐行读取 二、写入文件2.1 写入空文件2.2 写入多行2.3 附加到文件 遇到看不明白的地方,欢迎在评论中留言呐,一起讨论,一起进步! 本文参考:《Python编程:从入…...

WebForms 母版页
WebForms 母版页 介绍 WebForms 母版页是 ASP.NET WebForms 应用程序中的一项功能,它允许开发人员创建一个包含页面布局和控件的模板,其他页面可以继承这个模板。使用母版页可以确保整个网站的一致性和减少重复代码。 如何创建母版页 在 Visual Stud…...

Java应用打包成Docker镜像
# 使用官方的OpenJDK17镜像作为基础镜像 FROM openjdk:17 # 设置工作目录 WORKDIR /app # 复制本地的Java应用程序文件到镜像中的指定目录 COPY target/bear-module-system-0.0.1-SNAPSHOT.jar /app/bear-module-system-0.0.1-SNAPSHOT.jar # 暴露API端口 EXPOSE 8888 …...

什么是自动驾驶中的CopyCat?
"CopyCat"这个词通常有两个含义: 字面意思:它可以指一个模仿别人的人,就像猫一样模仿其他猫的行为。在日常用语中,如果有人说某人是个"copycat",他们可能是在说这个人缺乏原创性,总是模仿别人的想法、风格或者行为。 心理学和犯罪学中的含义:在心…...

为什么没人详细说过智能猫砂盆?最受欢迎的好用智能猫砂盆解析!
不知道大家有没有发现,在快节奏的现代生活中,忙碌于上班的我们会发现自己越来越难以抽出足够的时间去细心照料自己的猫咪。每次下班回家,看到猫砂盆里堆积的粪便和尿液,自己都感到一阵头痛。这时,我开始考虑起智能猫砂…...
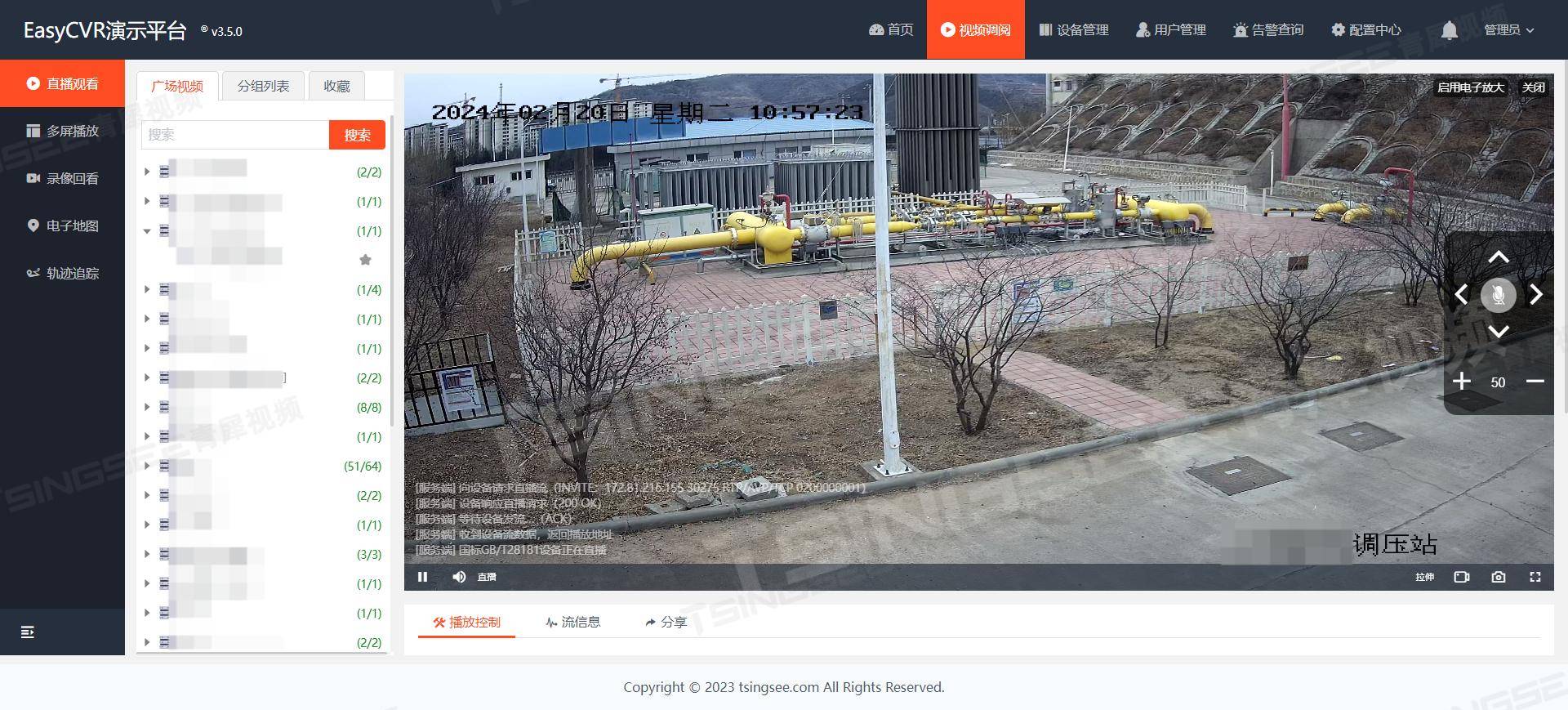
AI视频智能监管赋能城市管理:打造安全有序的城市环境
一、方案背景 随着城市化进程的加速和科技的飞速发展,街道治安问题日益凸显,治安监控成为维护社会稳定和保障人民安全的重要手段。当前,许多城市已经建立了较为完善的治安监控体系,但仍存在一些问题。例如,监控设备分…...
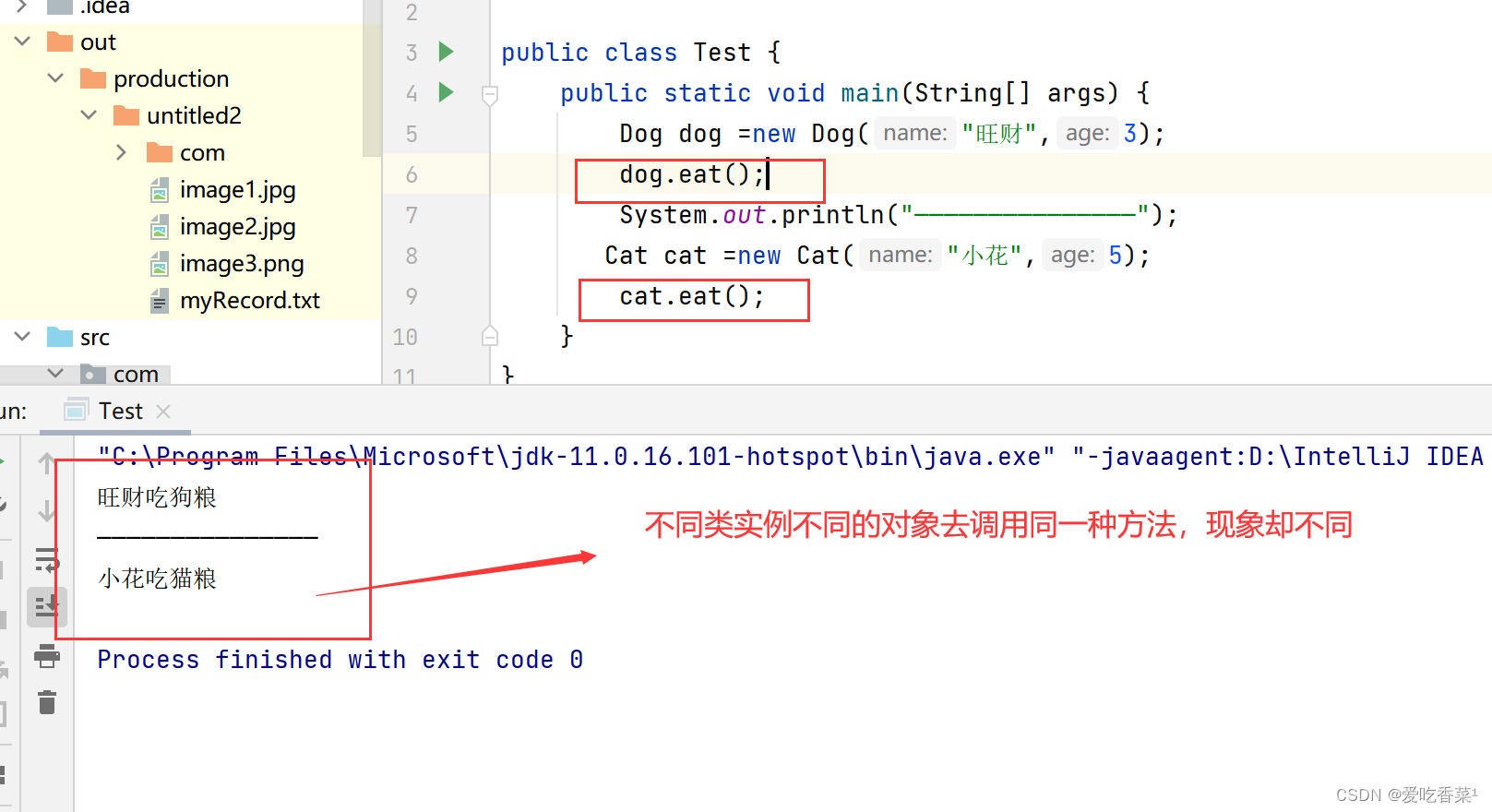
多态性(Java)
本篇学习面向对象语言的第三个特性——多态。 目录 1、多态的概念 2、继承多态实现条件 3、重写 4、重新与重载的区别: 5、向上转移和向下转型 5、1向上转型: 5、2 向下转型 1、多态的概念 多态的概念:通俗来说,就是多种形态…...

国际期货行情相关术语
1)合约:期货行情表提供了期货交易的相关信息 ,行情表中每一个期货合约都有合约代码(由期货合约交易代码和合约到期月份组成)来标识。 (2)开盘价:当日某一期货合约交易开始前五分钟集…...

LeetCode20.有效的括号
题目描述 分析 我们刚上来的思路可能是:找出这三种括号的个数 如果都是偶数 说明匹配 但是这里还有一个顺序问题 比如 " )( "这样是不匹配的! 所以这种思路不可取! 我们想 如果遇到左括号,把他读到一个顺序表中&#…...

尚玩助手广告变现app开发
尚玩助手广告变现app的开发涉及到多个关键环节。首先,市场调研与定位是不可或缺的步骤,通过了解当前市场上流行的小游戏类型、用户偏好以及竞争对手的情况,来确定app的定位和目标用户群体。 其次,游戏设计与规划也是关键的一环&a…...
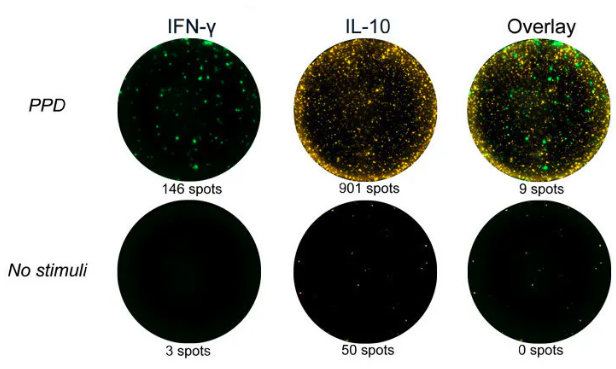
Anti-human IL-10 mAb (12G8), biotin:Mabtech热销品
Anti-human IL-10 mAb (12G8), biotin该单克隆抗体能够在ELISpot、FluoroSpot和ELISA等免疫分析方法中特异性检测人白介素10(IL-10)。可以将该单克隆抗体12G8作为检测抗体与单克隆抗体9D7(ca#3430-3)作为捕获抗体配对用于ELISpot、…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
