计算机图形学入门16:曲线
1.曲线
曲线(Curves)在图形学中应用非常广泛,比如:相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示,是使用曲线到矢量字体的应用,通过移动一些控制点来改变字体。

2.贝塞尔曲线
2.1 贝塞尔曲线定义
从上图中,如果无限的放大曲线的某一块区域,任何地方都是光滑的。这就是贝塞尔曲线(Bezier Curves)。
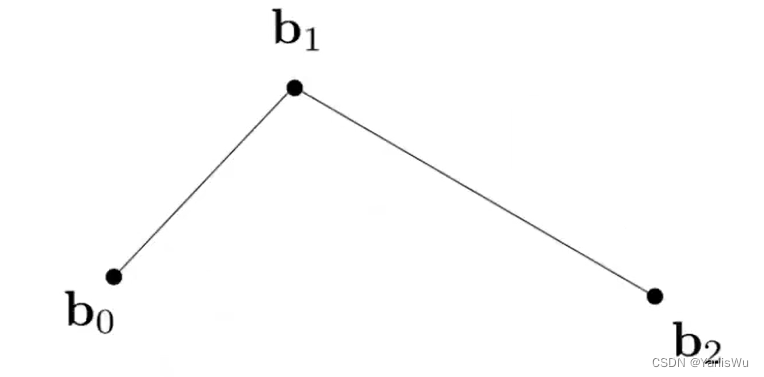
贝塞尔曲线是通过一系列控制点进行定义的曲线。而这些控制点满足一些性质,比如要满足从P0点开始,并且沿着P0P1方向,结束沿着P2P3方向,到P3点结束。曲线不必经过所有控制点,但必须经过起始点和结束点。这样就定义了一条贝塞尔曲线,如下图所示。
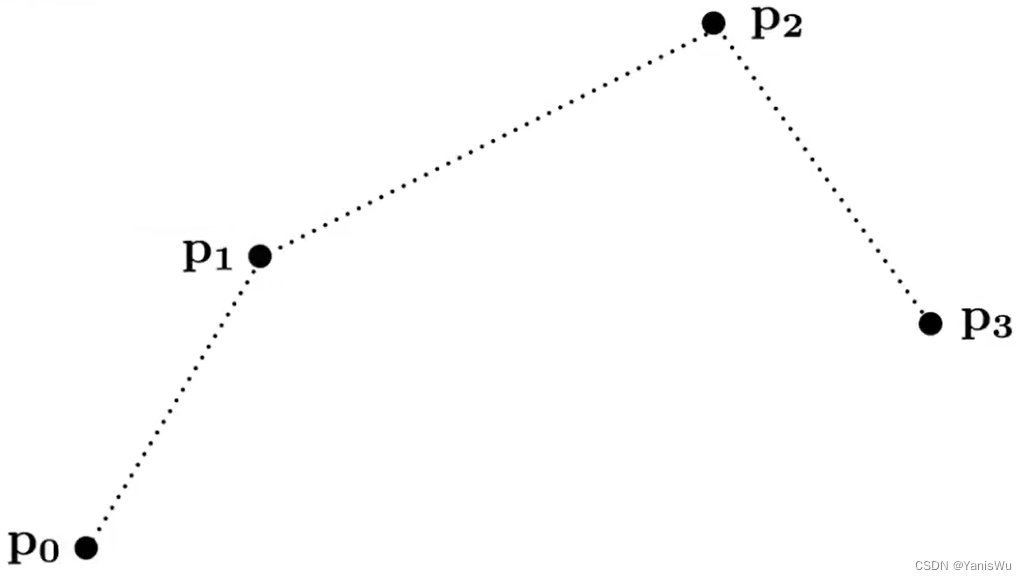
2.2 绘制贝塞尔曲线
那么,如何使用任意点绘制贝塞尔曲线呢?
贝塞尔曲线的绘制算法是 De Casteljau's Algorithm,算法的基本思想是利用线性插值的原理,将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合。
下面,我们以 3 个控制点绘制贝塞尔曲线的例子来进行介绍。
N 个控制点绘制的贝塞尔曲线,称为 N-1 阶贝塞尔曲线。如下图所示,我们定义了 3 个控制点,由此绘制的贝塞尔曲线称之为 二阶贝塞尔曲线(Quadratic Bezier)。对于这 3 个控制点,我们首先对相邻控制点进行连线。
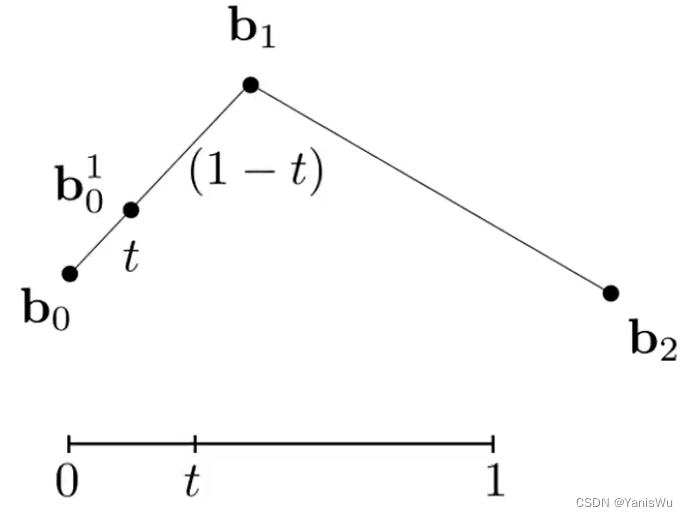
定义一个变量 t,其值的范围为 [0, 1],作为算法的输入值。当 t = 0 时,表示贝塞尔曲线起始点的输入值,当 t = 1 时,表示贝塞尔曲线结束点的输入值。所以算出 t 对应的所有点即可获得别塞尔曲线。
我们在控制点所构成的各个连线上定义一个点,这个点的位置取决于 t 的值,即一个比例值。如下图所示,在 b0b1 线段上定义一个 b10 点,并在 b1b2 线段上定义一个 b11 点。
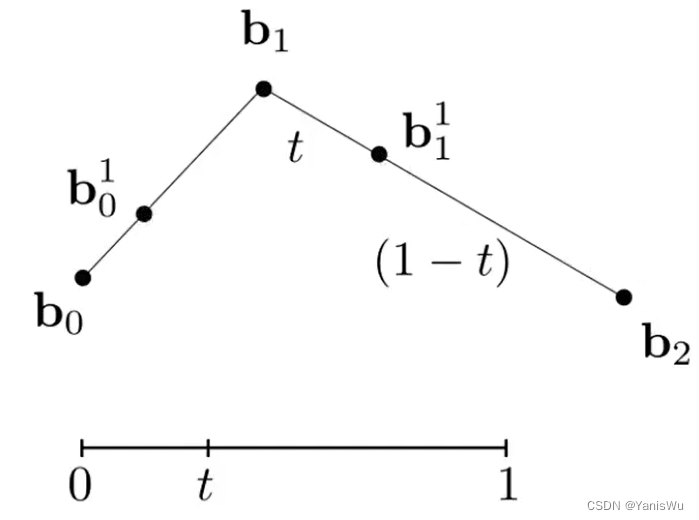
然后,对 b10 点和 b11 点进行连线,按照上述规则,在 b10b11 线段上定义一个 b20 点,找到最后一个点就结束了。如下图所示。

当新定义的点只有一个时,我们可以将 t 的值逐步从 0 变到 1。在这个过程中,b10、b20、b11 的位置都会随着 t 的变化而变化。对于最终的贝塞尔曲线,我们只需要关注最后定义的点 b20 的路径即可。
当我们扩展至更多控制点时,比如 4 个控制点时,我们仍然按照上述规则来处理,将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合,最终绘制曲线。如下图所示。
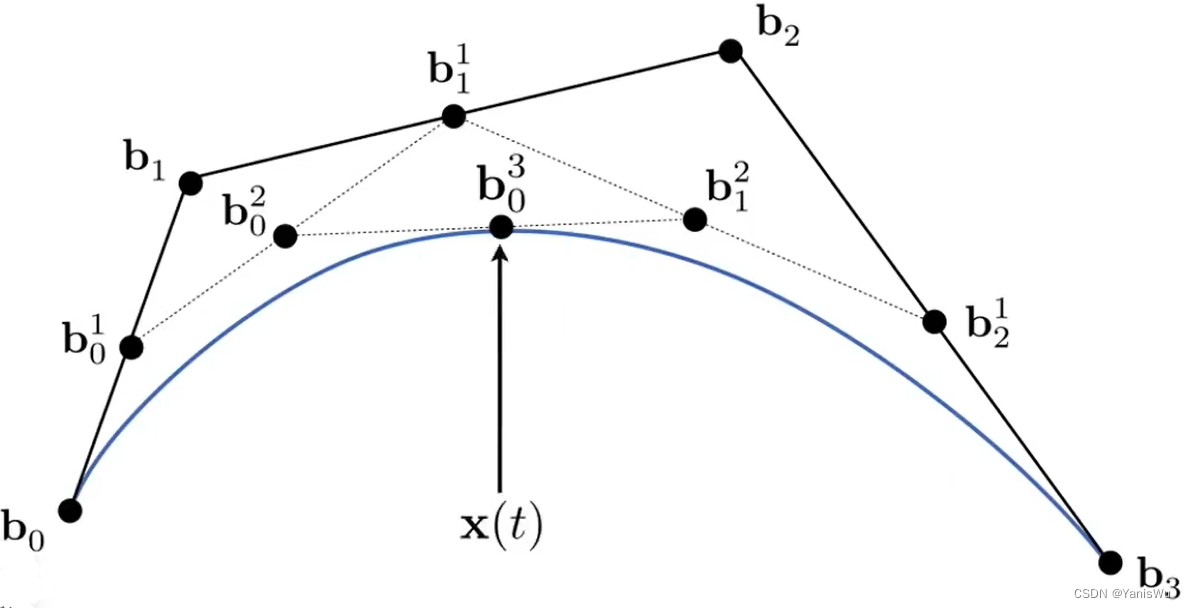
从上述可知,贝塞尔曲线也属于显式几何表示,因为显式几何表示通过直接定义或者参数定义,而这个 t 就是属于参数。
2.3 贝塞尔曲线代数公式
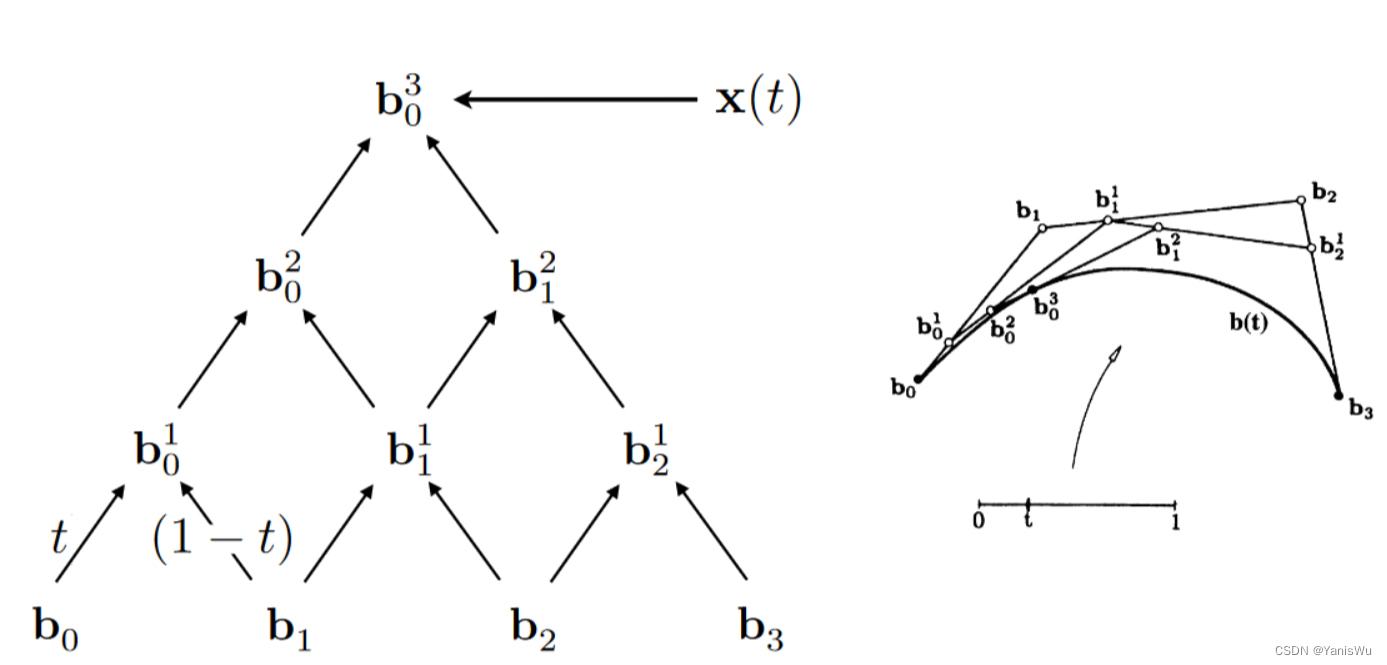
如上图所示,De Casteljau算法给出了一个系数金字塔,从中可知通过不断线性插值得到最后一个值的算法。那么,就可以写出这个关系式,以三个控制点为例,如下图所示。
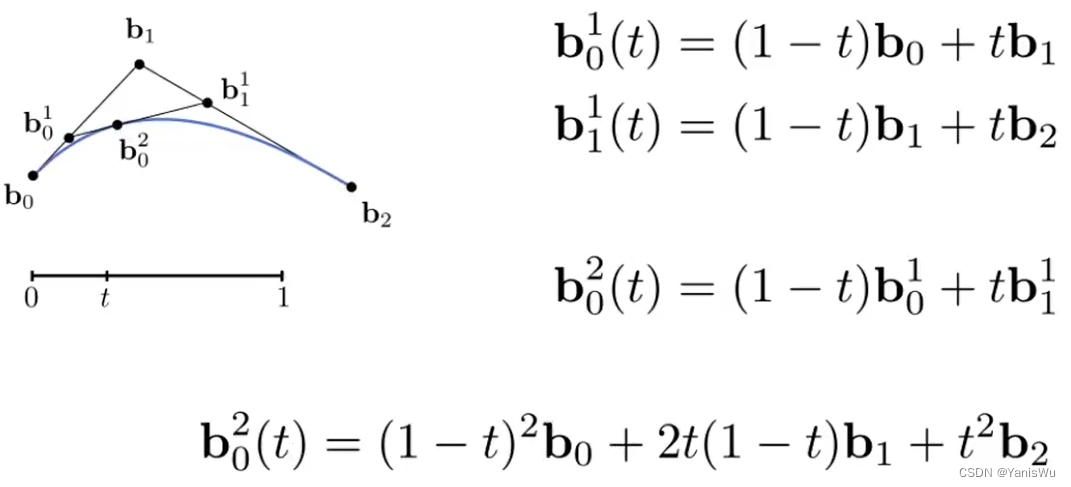
由此,我们可以推导出 N 阶贝塞尔曲线的代数公式,如下图所示。其中,n 表示 N 阶贝塞尔曲线(n+1个控制点), 表示控制点,
为伯恩斯坦多项式(Bernstein Polynomials)。
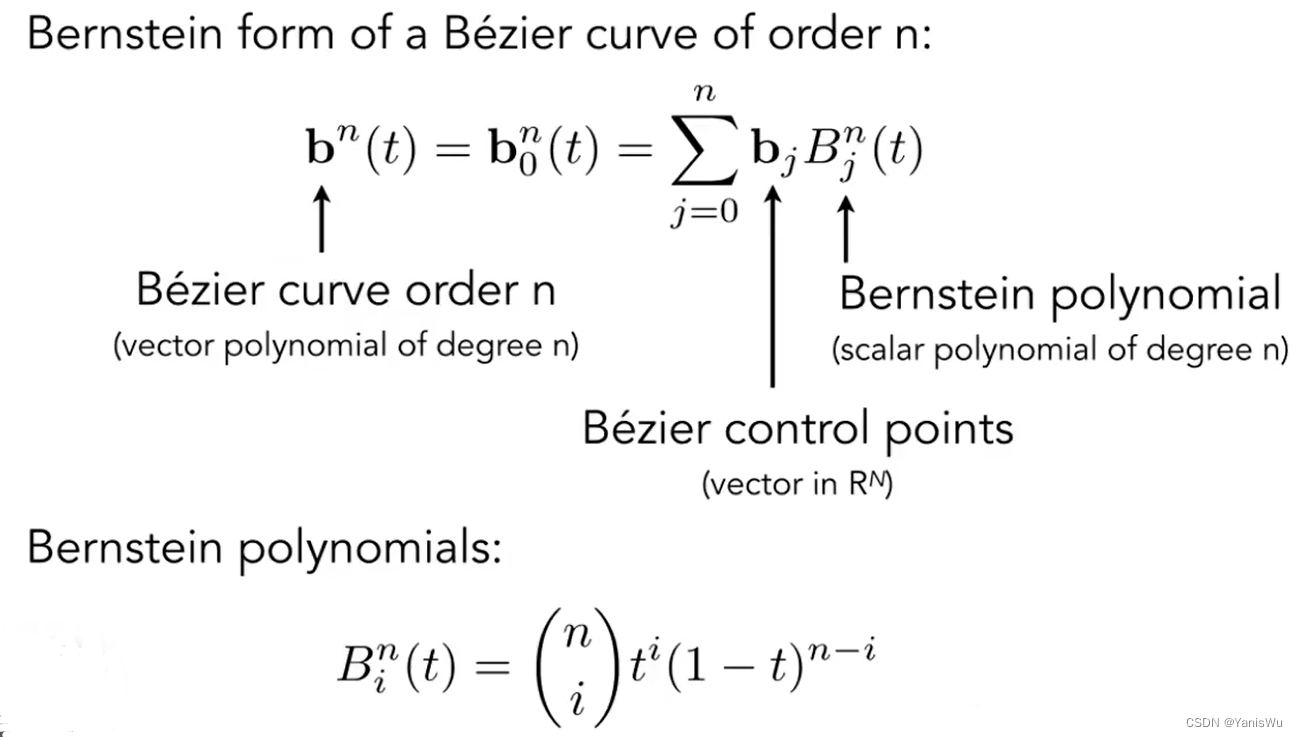
举个例子,假设n=3,那么可以有四个控制点,点的位置不局限于平面上,甚至在三维空间中,展开公式如下。
![]()
对于伯恩斯坦多项式,也可得出如下关系。
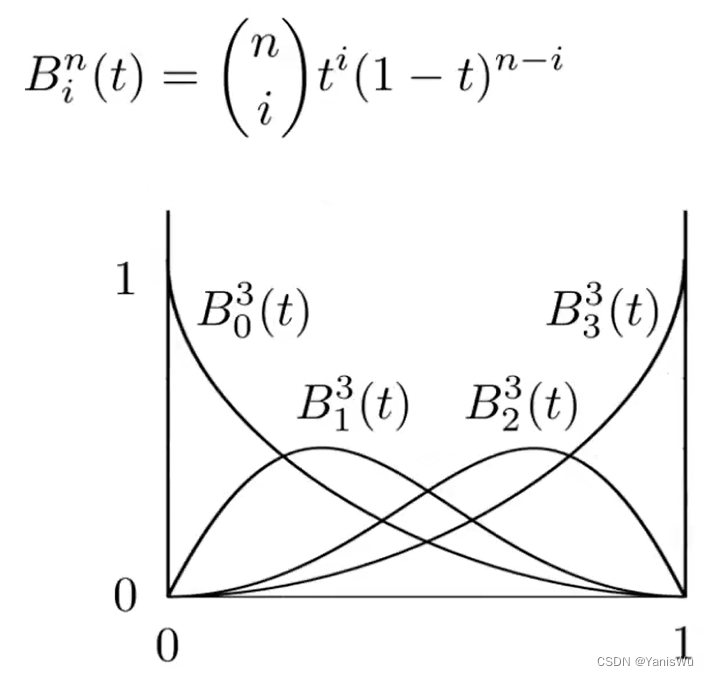
2.4 贝塞尔曲线的性质
1.一定过起点和终点。在t=0的时候一定在起点,t=1的时候一定在终点。
![]()
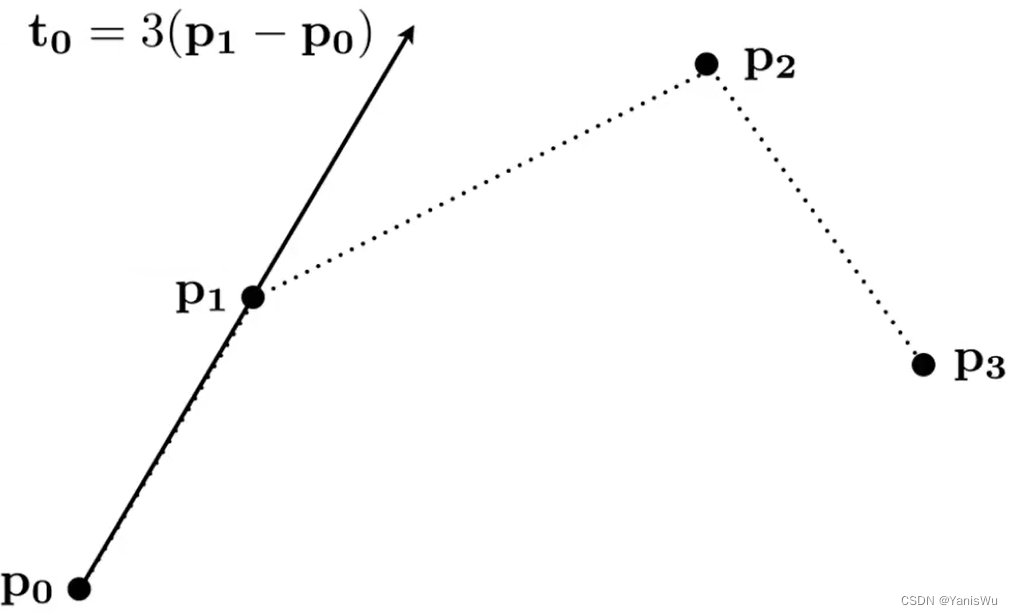
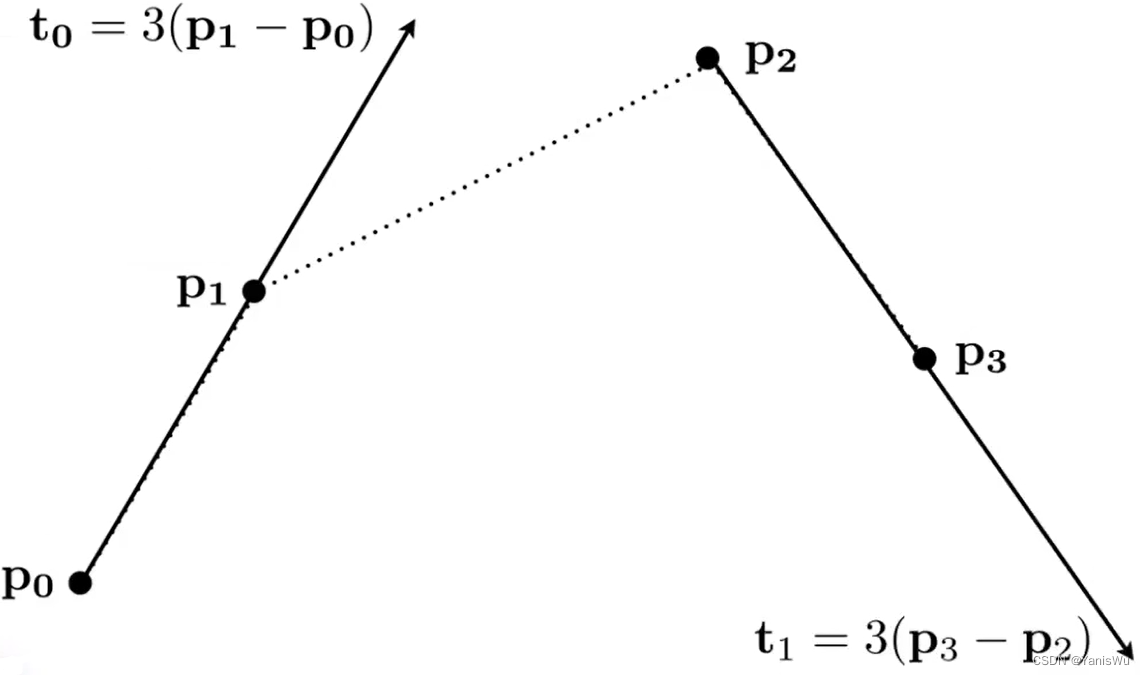
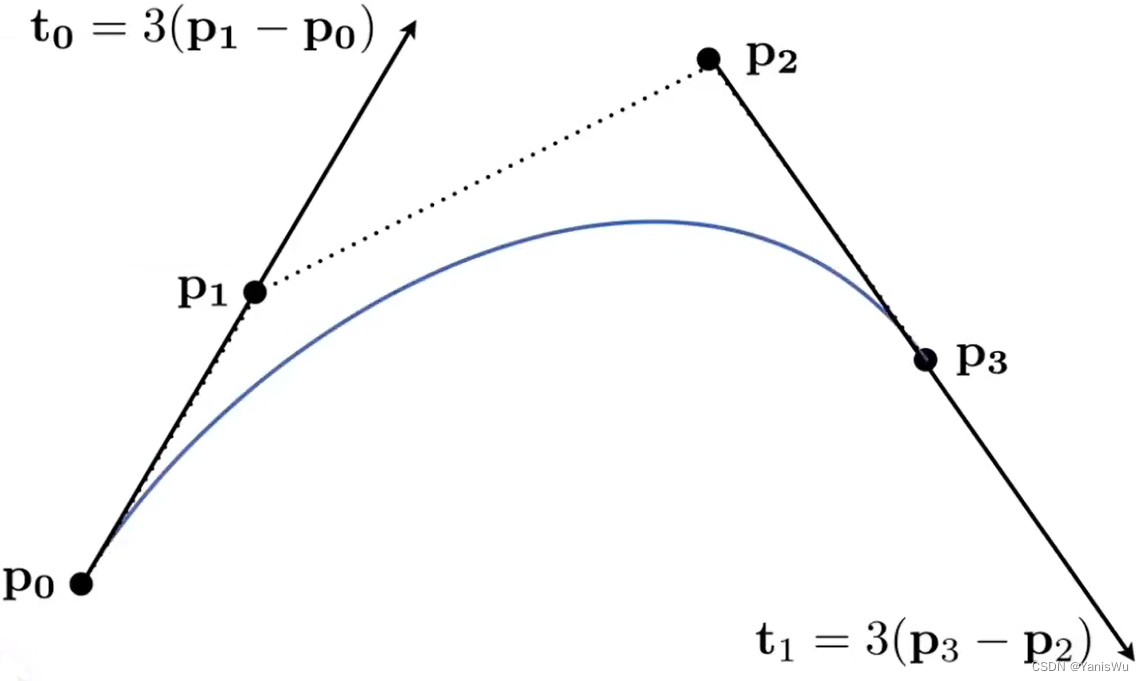
2.起始的切线方向是由起始点和第二个点求出,结束的切线方向是由结束点和倒数第二个点求出。以四个控制举例如下,3倍只是代表4个控制点。
![]()
3.不受仿射变换影响,受投影变换影响。
对贝塞尔曲线上的每个控制点做仿射变换,绘制的新曲线于原曲线一样。
在空间中绘制一条贝塞尔曲线,将控制点投影到相机看到的平面上,然后重新绘制的新曲线与原曲线不同。
4.凸包(Convex Hull)性质:贝塞尔曲线在所有控制点的凸包范围内。如下图所示,蓝色线就是形成的凸包,凸包就是能够包围一系列几何形体的最小的凸多边形。简单理解就是一扇门上订满了钉子,然后用一块橡皮筋将外面一圈包起来,松手后橡皮筋会收缩,收缩后的外框就是凸包。
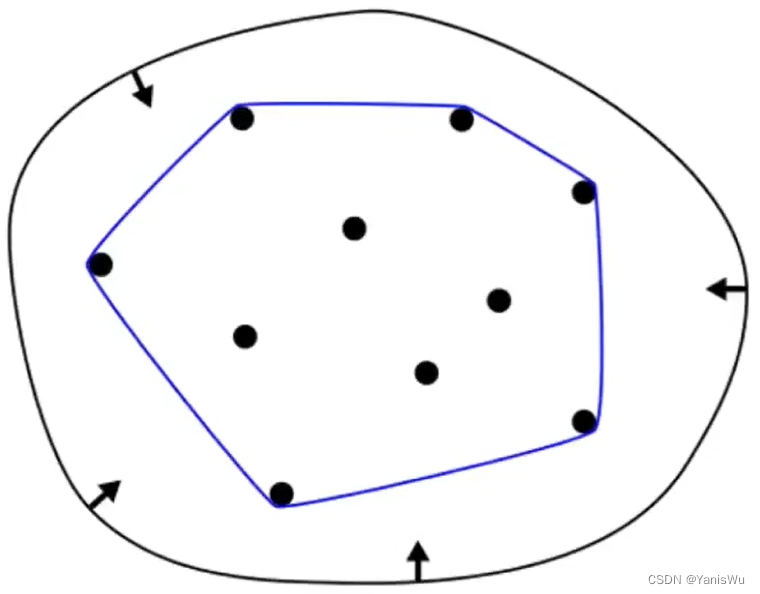
假设有一系列从走到右排列的点,排列在一条线上,这些是绘制贝塞尔曲线的控制点,那么绘制的贝塞尔曲线应该是什么形状?根据凸包性质,这条线就是凸包,而贝塞尔曲线不能超过凸包的范围,贝塞尔曲线被限制在这条线上,所以这条线就是贝塞尔曲线。
3.分段贝塞尔曲线
3.1 定义
如下图所示,给了11个点(n+1),绘制一条贝塞尔曲线(蓝色线)。可以看到这条贝塞尔曲线并不直观,非常平滑,说明当控制点多的时候,贝塞尔曲线很难得到想要的形状。
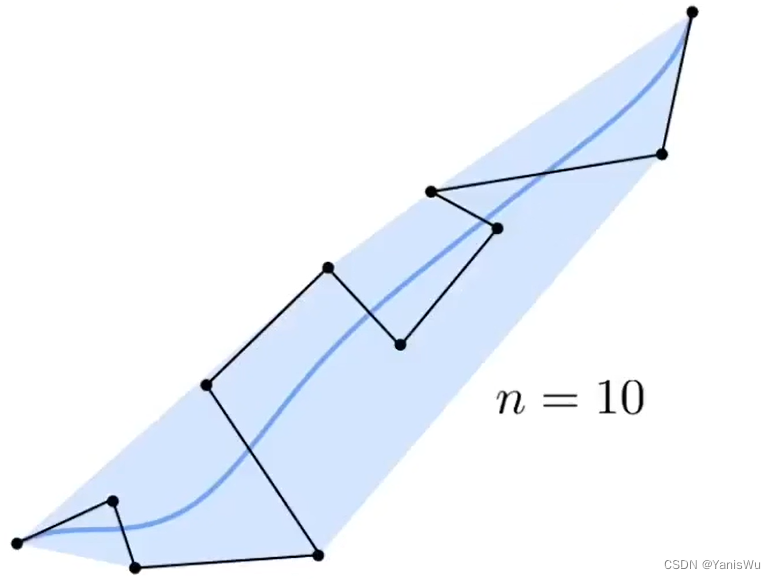
所以,当控制点比较多时,每次用很少的控制点绘制去绘制,然后将绘制的连接成一条贝塞尔曲线。于是就有了分段贝塞尔曲线(Piecewise Bezier Curves),即采用多条贝塞尔曲线进行串联。用4个常控制点来绘制一条贝塞尔曲线,也就是三阶贝塞尔曲线(Cubic Bezier)。如下图所示。

在PS里钢笔工具画曲线就是这个应用。
3.2 平滑处理
如下图所示,是一条分段贝塞尔曲线,而且每4个点绘制一条三次贝塞尔曲线。
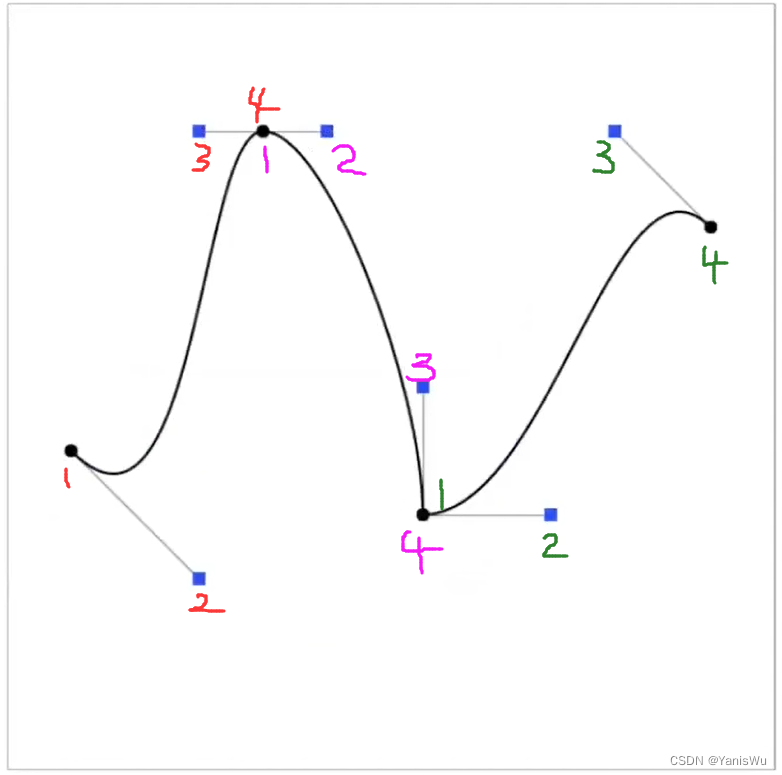
可以发现有连接点的曲线出现了转折,不够平滑,那么如何保证连起来的曲线是平滑的呢?只要保证曲线结束的切线方向与相连曲线起始的切线相同即可(方向大小都相同),也就是导数要连续。
根据贝塞尔曲线的性质:三次贝塞尔曲线的起始切线的方向由第一个点和第二个点求得,结束切线的方向由第三个点和第四个点求出,并且前面有系数3。而相连的两条曲线,前一条曲线的结束点就是后一条曲线的起始点,所以需要调整前一条曲线的第三个点与后一条曲线的第二个点位置,使其切线相同。
3.3 连续性
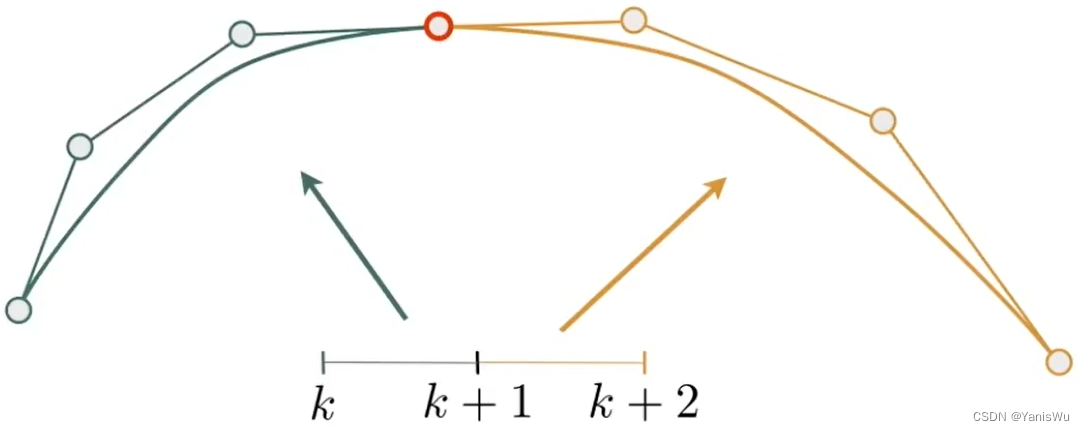
如下图所示,在几何上两条三次贝塞尔曲线相连通过一个控制点,这是一种最简单的连续。像这种第一段的终点等于第二段的起点叫做连续(Continuity)。
连续关系式:
![]() 。
。表示上一段曲线终点,
表示下一段曲线起点。
那么,在几何连续外,还需要切线的连续(切线相同,方向和大小都相同)。这叫做连续,也就是一阶导数的连续。如下图所示。
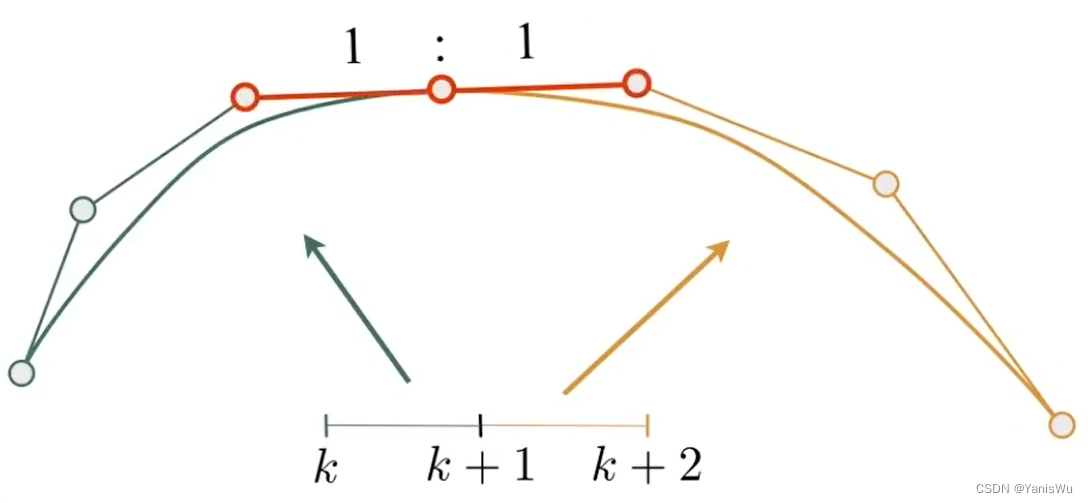
连续关系式:
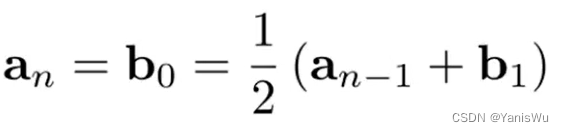 。
。
除了一阶导数连续,还有2阶导数连续,也叫做曲率连续(连续)。
综上, 连续为两个函数在值上连续,
连续为导数上的连续,
为二阶导数连续,以此类推。
4.样条曲线
4.1 定义
样条(Spline)曲线一种连续的曲线,通过一系列的控制点控制,在任意位置满足一定的连续性,也就是一定数量的连续导数(任意阶)。
简而言之,这是一条可控的曲线。

4.2 B样条曲线
B样条(B-Splines)是基础样条(Basis Splines)的缩写,就是基函数样条。可以理解成用伯恩斯坦多项式在时间 t 里几个不同项对不同的控制点做一个加权平均,也可以理解成不同控制点位置对伯恩斯坦多项式进行加权求和。那么,这个伯恩斯坦多项式就可以理解为基函数。基函数就是由不同函数通过不同方式组合起来可以形成别的函数。
B样条曲线相当于是贝塞尔曲线的一个扩展。贝塞尔曲线在控制点很多的情况下,移动其中任何一个点,整个曲线在任何位置都会发生变化。假如只需要移动一个控制点改变一小段曲线的形状,也就是局部性,而B样条曲线能够满足这个功能,比分段贝塞尔曲线更方便。
B样条需要比贝塞尔曲线更多的信息。比贝塞尔曲线更加复杂,这里不做详细介绍。
相关文章:

计算机图形学入门16:曲线
1.曲线 曲线(Curves)在图形学中应用非常广泛,比如:相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示,是使用曲线到矢量字体的应用,通过移动一些控制点来改变字体。 2.贝塞尔曲线 2.1 贝…...
【Ruby基础01】windows和termux中搭建Ruby开发环境
windows下环境搭建 railsinstaller官方git地址 按照文档安装git、nodejs、yarn,安装教程百度一下。railsinstall可以从release页面下载最新版本4.1.0。 安装完成如下 安装RubyMine 下载RubyMine RubyMine下载地址 安装激活 下载文件,按照里面的流程…...

2406c++,iguana动态反射
原文 iguana是一个基于编译期反射的序化库,支持从结构序化到不同数据格式. iguana可序化一个C结构到json,xml,yaml和protobuf格式.这都是通过编译期反射实现的. 现在iguana也支持了动态反射,主要特征: 1,通过对象名创建对象实例 2,取对象所有字段名 3,根据字段名取字段值 4,根…...

干货分享——AB站帮你解决独立站收款难题
目前,国内已经有抖音、拼多多和淘宝平台推出“仅退款”售后服务,无疑是加剧了原本就在疯狂打价格战的国内电商的严峻现状,使得商家不得不担心被顾客“薅羊毛”。在国内电商环境严重“内卷”的情况下,拓宽海外市场不失为一大妙计。…...

C++继承与派生
1.基本知识 类的继承是新类从已有类那里获得特性,从已有的类产生新类的过程称为类的派生; 已有类称为基类或父类,派生出的新类则称为派生类或子类; 继承的功能: (1)使得基类与派生类之间建立…...

Survival Animations
一套生存游戏的动画集,包括采集、建造、捕鱼、剥皮/鞣制、篝火等更多内容。 总动画数:89 建造/制作 30 篝火 28 饮水 3 水壶 3 觅食 2 治疗 3 空闲 1 原始捕鱼 7 剥皮 1 矛捕鱼 4 伐木 5 下载:Unity资源商店链接资源下载链接 效果图:...

Cargo 教程
Cargo 教程 1. 引言 Cargo 是 Rust 编程语言的包管理器和构建工具。它为 Rust 项目提供了依赖管理、编译和打包等功能。本教程将详细介绍 Cargo 的基本用法,帮助您快速上手 Rust 项目开发。 2. 安装 Cargo 在开始使用 Cargo 之前,您需要确保已经安装了 Rust 编程语言。Ru…...
linux中“PXE高效批量装机”
在大规模的 Linux 应用环境中,如 Web 群集、分布式计算等,服务器往往并不配备光驱设备,在这种情况下,如何为数十乃至上百台服务器裸机快速安装系统呢?传统的 USB光驱、移动硬盘等安装方法显然已经难以满足需求。 PXE …...
emm, ComfyUI的作者从Stability.AI离职了
🍖背景 今天在更新ComfyUI的过程中,看到Manager中有这样一段描述: 嗯?做了新的官方网站?然后开始新篇章? 难道说ComfyUI的作者从Stability.AI离职了? 赶紧点开链接看了下,emm&…...
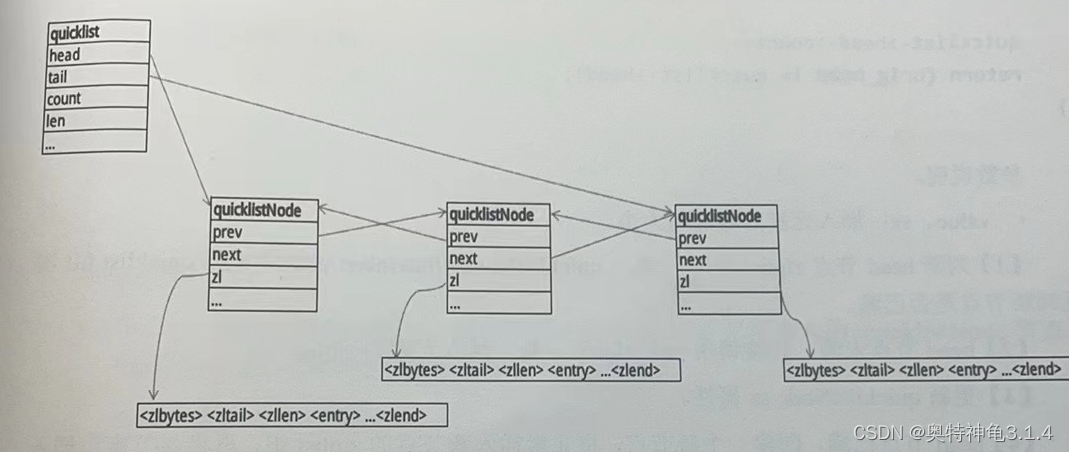
Redis-五种数据结构之列表(ziplist、quicklist)
列表 文章目录 列表压缩列表-ziplistziplist 定义级联更新 快速列表-quicklistquicklistNode 定义quicklist 定义quicklist常用操作其他操作quicklist 相对于普通链表优点quick应用场景在redis 中使用quicklist 列表数据类型可以存储一组按插入顺序排序的字符串,他很…...
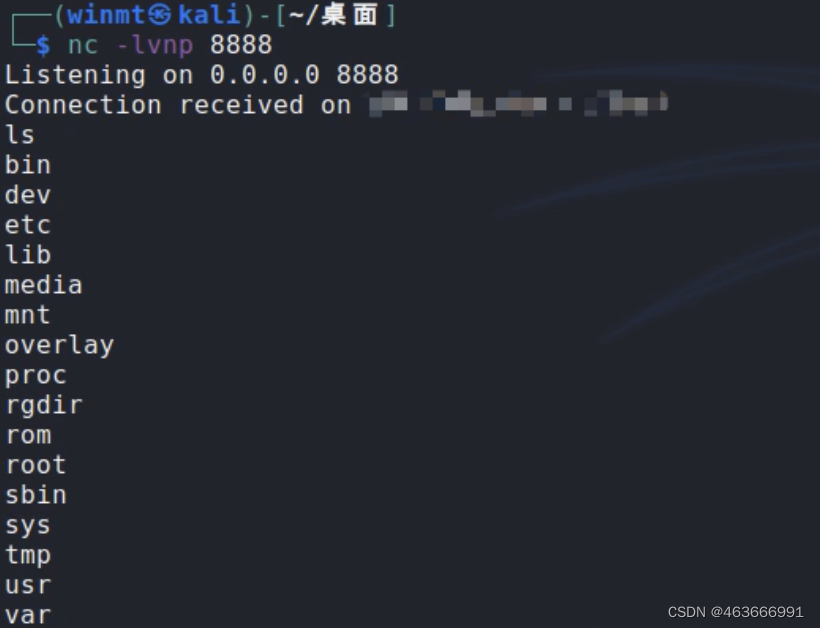
记一次全设备通杀未授权RCE的挖掘经历
想来上一次挖洞还在一年前的大一下,然后就一直在忙活写论文,感觉挺枯燥的(可能是自己不太适合弄学术吧QAQ),所以年初1~2月的时候,有空的时候就又会挖一挖国内外各大知名厂商的设备,拿了几份思科…...

【数据库编程-SQLite3(一)】sqlite3数据库在Windows下的配置及测试
学习分析 1、资源准备2、环境配置2.1、将资源包下载解压缩保存。2.2、在QT中创建工程,配置环境 3、测试配置3.1、 sqlite3_open函数3.2、sqlite3_close函数3.3、代码测试 1、资源准备 资源包 2、环境配置 2.1、将资源包下载解压缩保存。 解压缩得到以下文件 2.2、在QT中创建…...

YOLOv10改进 | 主干篇 | YOLOv10引入华为VanillaNet替换Backbone
1. VanillaNet介绍 1.1 摘要: 基础模型的核心是“越多越好”的理念,计算机视觉和自然语言处理领域取得的惊人成功就是例证。 然而,优化的挑战和变压器模型固有的复杂性要求范式向简单性转变。 在这项研究中,我们介绍了 VanillaNet,一种设计优雅的神经网络架构。 通过避免…...

C++ 迷宫问题
描述 定义一个二维数组 N*M ,如 5 5 数组下所示: int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走…...

【Linux】Linux文件系统中主要文件夹列举_作用说明
在Linux系统中,文件夹(或称为目录)的组织结构是系统功能和用户数据的重要组成部分。以下是Linux系统中一些主要文件夹的列举及其作用说明: / (根目录): 是Linux文件系统的起点。通常只包含其他目录,不建议直接在其中存…...

移植案例与原理 - HDF驱动框架-驱动配置(1)
HCS(HDF Configuration Source)是HDF驱动框架的配置描述源码,内容以Key-Value为主要形式。它实现了配置代码与驱动代码解耦,便于开发者进行配置管理。应该,类似Linux DTS(Device Tree Source)设备树。 HC-GEN(HDF Configuration Generator)是…...
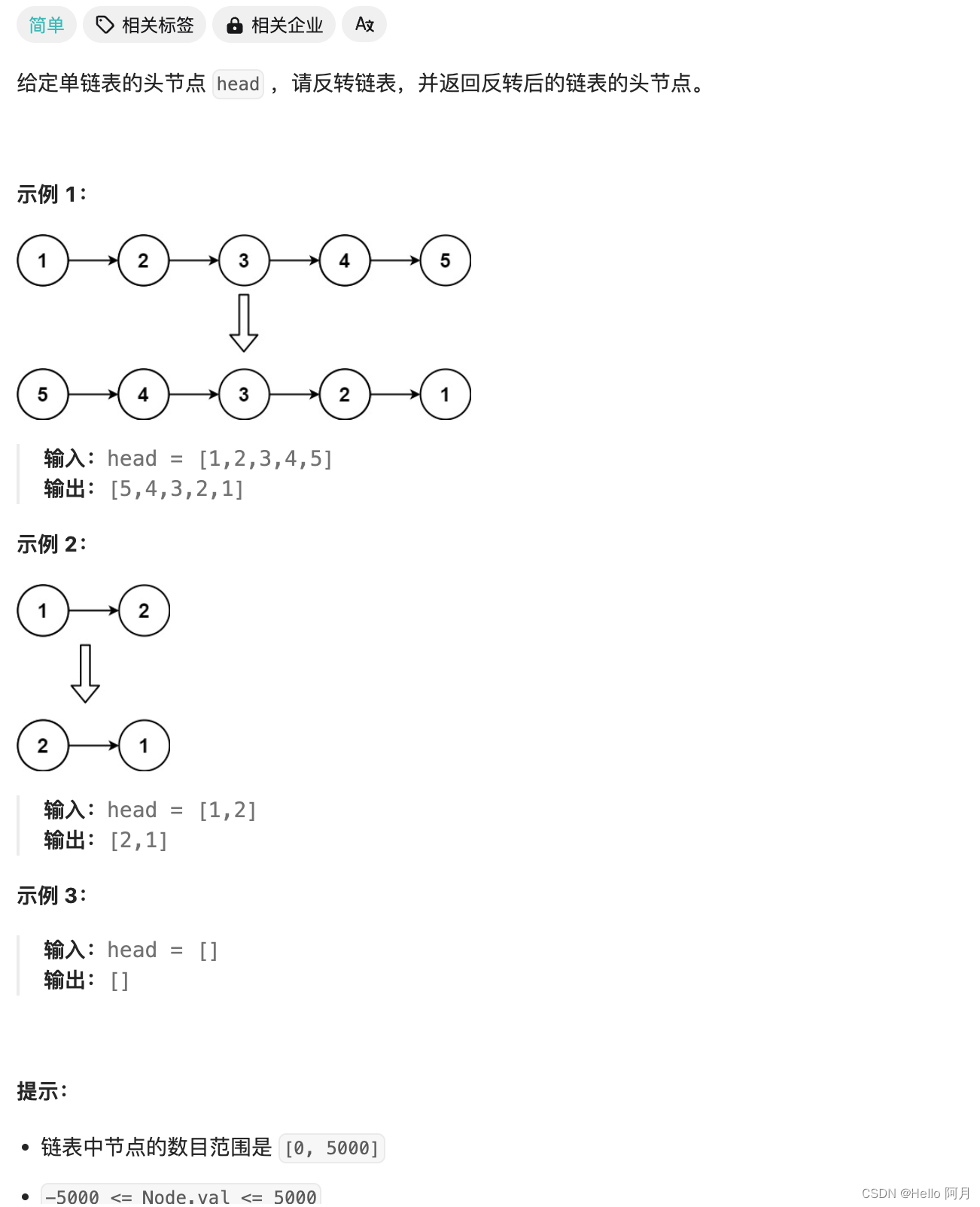
坚持刷题|反转链表
文章目录 题目思考实现1. 迭代方式实现链表翻转2. 递归方式实现链表翻转 Hello,大家好,我是阿月。坚持刷题,老年痴呆追不上我,今天继续链表:反转链表 题目 LCR 024. 反转链表 思考 翻转链表是一个常见的算法问题&a…...
升级和维护老旧LabVIEW程序
在升级老旧LabVIEW程序至64位环境时,需要解决兼容性、性能和稳定性等问题。本文从软件升级、硬件兼容性、程序优化、故障修复等多个角度详细分析。具体包括64位迁移注意事项、修复页面跳转崩溃、解决关闭程序后残留进程的问题,确保程序在新环境中的平稳运…...

sqlite数据库整体迁移进mysql整个流程并解决中文异常问题
咨询【QQ】 sqlite轻量数据还行,随着数据量增大,不得不迁移进mysql 首先 电脑执行 sqlite3 db.sqlite3 .dump > dump.sql 会把整个sqlite的数据导出进 dump.sql中 紧接着我们把sqlite的sql转换成mysql的sql语句,因为mysql语句和 sq…...

Hadoop3:MapReduce中的Partition原理及自定义Partition
一、默认Partition分区配置 以WC案例来进行验证。 1、设置setNumReduceTasks 修改的代码 这行代码,确定了reduceTask的数量,也确定了分区逻辑 在mapper文件中,打上断点 计算分区的代码 这里会对每一个kv进行计算,然后&#…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
