matlab线性多部法求常微分方程数值解
用Adamas内差二步方法,内差三步方法,外差二步方法,外差三步方法这四种方法计算。


中k为1和2.

k为2和3
代码
function chap1_adams_methodu0 = 1;
T = 2;
h = 0.1;
N= T/h;
t = 0:h:T;
solu = exact1(t);f = @f1;
u_inter_2s = adams_inter_2steps(f,u0,t,h,N);
u_extra_2s = adams_extra_2steps(f,u0,t,h,N);
figure(1)
plot(t,u_inter_2s,'*',t,u_extra_2s, 'o',t, solu,'r')
legend('Adams-inter-2s', 'Adams-extra-2s','Exact-soln')u_inter_3s = adams_inter_3steps(f,u0,t,h,N);
u_extra_3s = adams_extra_3steps(f,u0,t,h,N);
figure(2)
plot(t, u_inter_3s,'*', t, u_extra_3s, 'o', t, solu, 'r')
legend('Adams-inter-3s', 'Adams-extra-3s', 'Exact-soln')endfunction u = adams_inter_2steps(f, u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
u(2) = exact1(1*h);
eps_in = 1e-6;
K_in = 6;
for n = 2:Nf_nm1 = f(t(n-1),u(n-1));f_n = f(t(n), u(n));s1 = u(n);du = 1;k = 1;
while abs(du)>eps_in & k<K_ins2 = u(n) + h*( 5*f(t(n+1), s1)+ 8*f_n - f_nm1 )/12;du = s2- s1;s1 = s2;k = k + 1;
end
u(n+1) = s2;
end
endfunction u = adams_inter_3steps(f, u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
% u(3) = u(2) + h*f(t(2), u(2)) ;
u(2) = exact1(1*h);
u(3) = exact1(2*h);
eps_in = 1e-6;
K_in = 6;
for n = 3:Nf_nm2 = f(t(n-2), u(n-2));f_nm1 = f(t(n-1), u(n-1));f_n = f(t(n), u(n)); s1 = u(n);du = 1;k = 1;
while abs(du)>eps_in & k<K_ins2 = u(n)+ h*(9*f(t(n+1),s1) + 19*f_n - 5*f_nm1 + f_nm2 ) /24;du = s2 - s1;s1 = s2;
k = k + 1;end
u(n+1) = s2;
end
endfunction u = adams_extra_2steps(f,u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
u(2) = exact1(h);
for n = 2:N
f_nm1 = f(t(n-1), u(n-1));
f_n = f(t(n), u(n));
u(n+1) = u(n)+ h*( 3*f_n - f_nm1 )/2;
end
endfunction u = adams_extra_3steps(f, u0,t, h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
% u(3) = u(2) + h*f(t(2), u(2));
u(2) = exact1(1*h);
u(3) = exact1(2*h);
eps_in = 1e-6;
for n = 3:N
f_nm2 = f(t(n-2), u(n-2));
f_nm1 = f(t(n-1), u(n-1));
f_n = f(t(n), u(n));
u(n+1) = u(n)+ h*( 23*f_n - 16*f_nm1 + 5*f_nm2 )/12;
end
endfunction f = f1(t, u)
f = -5*u ;
endfunction f = exact1(t)
f = exp(-5*t);
end
结果:

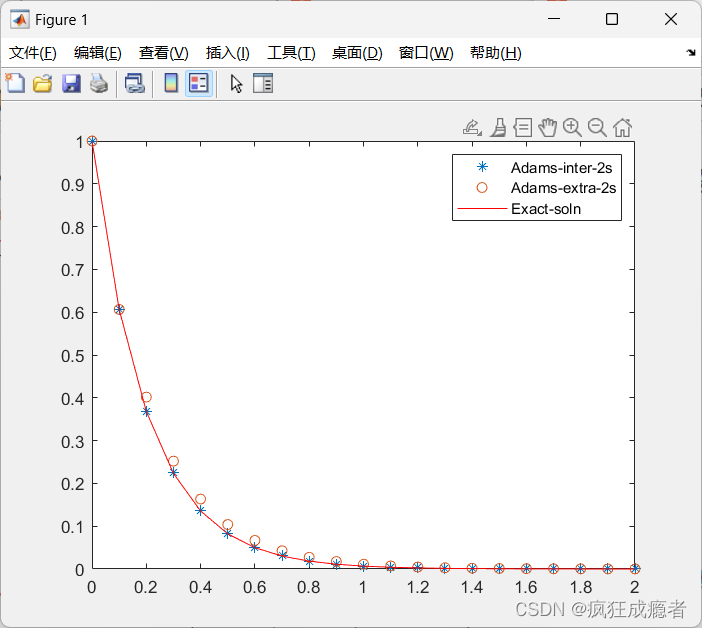
相关文章:

matlab线性多部法求常微分方程数值解
用Adamas内差二步方法,内差三步方法,外差二步方法,外差三步方法这四种方法计算。 中k为1和2. k为2和3 代码 function chap1_adams_methodu0 1; T 2; h 0.1; N T/h; t 0:h:T; solu exact1(t);f f1; u_inter_2s adams_inter_2steps(…...

前端页面实现【矩阵表格与列表】
实现页面: 1.动态表绘制(可用于矩阵构建) <template><div><h4><b>基于层次分析法的权重计算</b></h4><table table-layout"fixed"><thead><tr><th v-for"(_, colI…...

GPT4v和Gemini-Pro调用对比
要调用 GPT-4 Vision (GPT-4V) 和 Gemini-Pro,以下是详细的步骤分析,包括调用流程、API 使用方法和两者之间的区别,以及效果对比和示例。 GPT-4 Vision (GPT-4V) 调用步骤 GPT-4 Vision 主要通过 OpenAI 的 API 进行调用,用于处…...
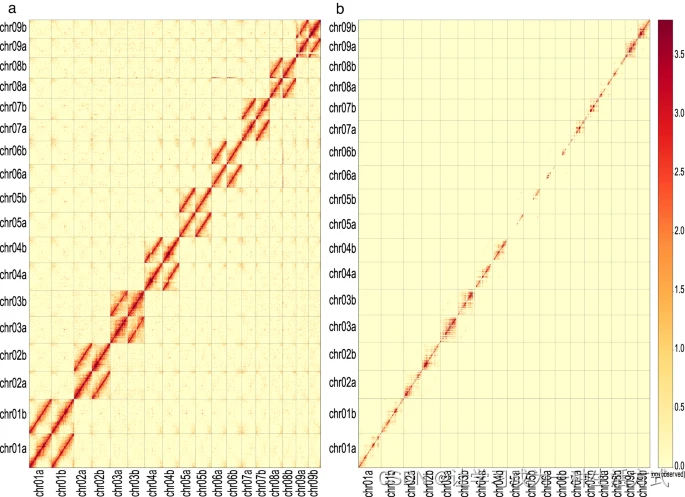
破布叶(Microcos paniculata)单倍型染色体级别基因组-文献精读22
Haplotype-resolved chromosomal-level genome assembly of Buzhaye (Microcos paniculata) 破布叶、布渣叶(Microcos paniculata)单倍型解析染色体级别基因组组装 摘要 布渣叶(Microcos paniculata)是一种传统上用作民间药物和…...
浅谈RC4
一、什么叫RC4?优点和缺点 RC4是对称密码(加密解密使用同一个密钥)算法中的流密码(一个字节一个字节的进行加密)加密算法。 优点:简单、灵活、作用范围广,速度快 缺点:安全性能较差&…...

uniapp微信小程序开发物料
开发工具 HBuilder: HBuilderX-高效极客技巧 vscode 1、在vscode中新建一个项目npx degit dcloudio/uni-preset-vue#vite-ts 项目名称 2、在HBuilder中可以可视化进行新建项目 路由 在app.json文件中配置pages路由路径 路由跳转方法 uni.navigateTo(OBJECT)…...
大数据工程师如何做到数据可视化?
好的数据可视化作品都是通过不断的数据对比分析实战出来的。 今天给大家带来一篇大数据工程师干货,从多角度解析做数据可视化的重要性,并解读一些适用的应用场景。大数据工程师们刷到这篇文章时一定要进来看看,满满的干货。 目录 1. 什么是数…...

Java 序列化与反序列化
Java 序列化是一种将对象的状态转换为字节流的机制,以便可以将该对象的状态保存到文件、数据库或通过网络传输。在反序列化过程中,这些字节流可以被重新转换为对象。序列化主要用于以下几种情况: 持久化存储:将对象的状态保存到文…...

自定义防抖注解
问题场景 在开发中由于可能存在的网络波动问题导致用户重复提交,所以自定义一个防抖注解。设计思路:自定义注解加在接口的方法上,注解中设置了SPEL表达式,可以通过SPEL表达式从接口参数中提取Redis的Key,以这个Key作为…...
【尚庭公寓SpringBoot + Vue 项目实战】登录管理(十八)
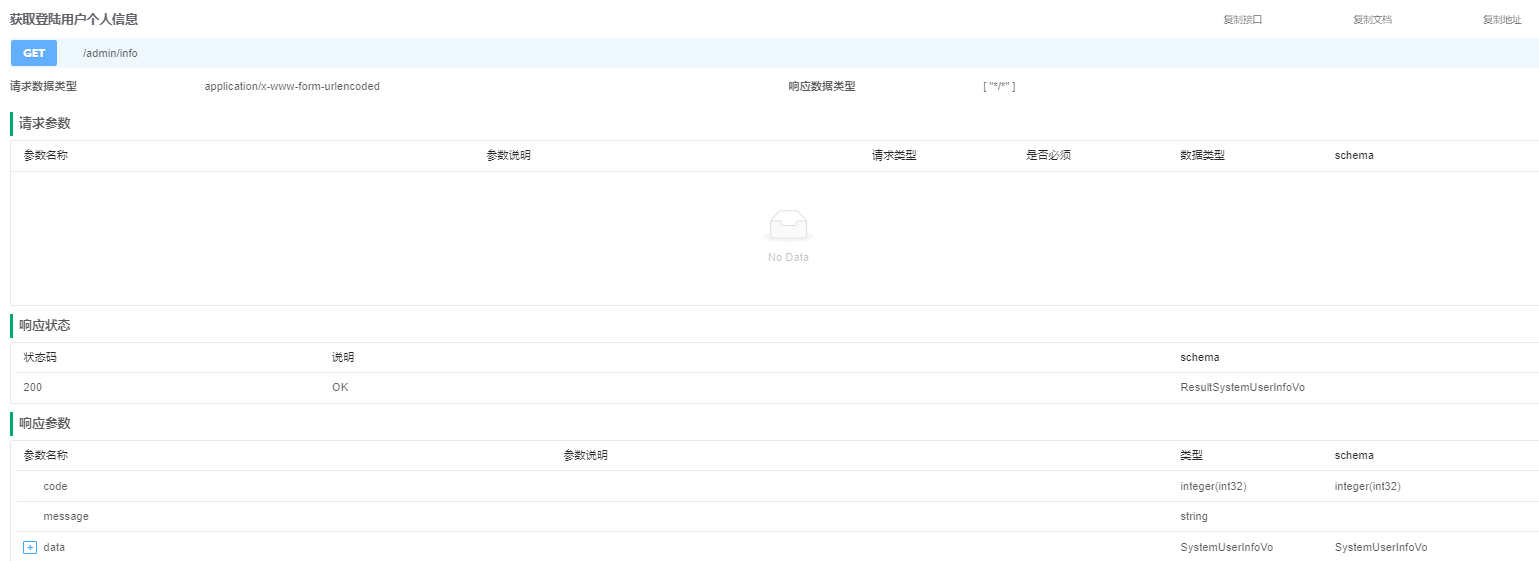
【尚庭公寓SpringBoot Vue 项目实战】登录管理(十八) 文章目录 【尚庭公寓SpringBoot Vue 项目实战】登录管理(十八)1、登录业务介绍2、接口开发2.1、获取图形验证码2.2、登录接口2.3、获取登录用户个人信息 1、登录业务介绍 登…...

【html】用html+css做地表最强王者荣耀辅助工具
源码: <!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title><style>* {margin: 0;padding: 0;}body{background-color: blue;}.con {width: 300px;height: 500px;background-color: rgba(230,…...
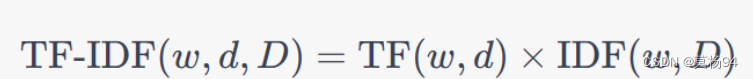
TF-IDF、BM25传统算法总结
1. TF-IDF算法 F-IDF(词频-逆文档频率)是一种用于衡量文本中词语重要性的方法,特别适用于信息检索和文本挖掘任务。下面会拆分为两部分深入讲解TF-IDF的计算过程,以便更好地理解。 TF-IDF的计算过程可以分为两个主要部分…...
项目五 OpenStack镜像管理与制作
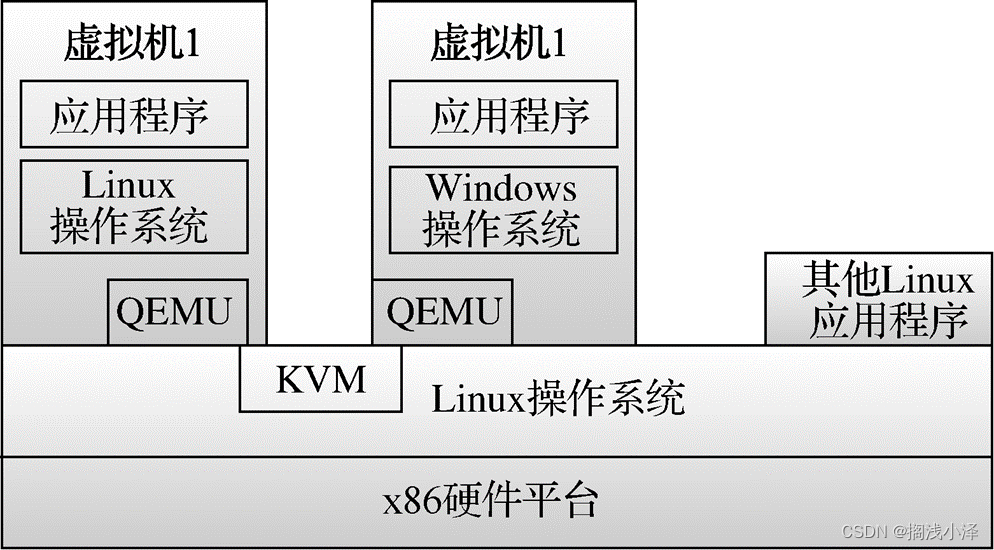
任务一 理解OpenStack镜像服务 1.1 •什么是镜像 • 镜像通常 是指一系列文件或一个磁盘驱动器的精确副本 。 • 虚拟机 所使用的虚拟磁盘, 实际上是 一种特殊格式的镜像文件 。 • 云 环境下尤其需要 镜像。 • 镜像 就是一个模板,类似于 VMware 的虚拟…...

LabVIEW回热系统热经济性分析及故障诊断
开发了一种利用LabVIEW软件的电厂回热系统热经济性分析和故障诊断系统。该系统针对火电厂回热加热器进行优化,通过实时数据监控与分析,有效提高机组的经济性和安全性,同时降低能耗和维护成本。系统的实施大幅提升了火电厂运行的效率和可靠性&…...

设计模式-迭代器模式
目录 一:基本介绍 二:原理说明 三:案例说明 四:优点 五:缺点 一:基本介绍 1)属于行为模式 2)如果我们的集合元素是用不同的方式实现的,有数组,还有java的集合类,或者还有其他方式,当客户 端要遍历这些集合元素的时候就要使用多种遍历方式,而且还会暴露元素的内部结构,可以…...
UV胶带和UV胶水的应用场景有哪些不同吗?
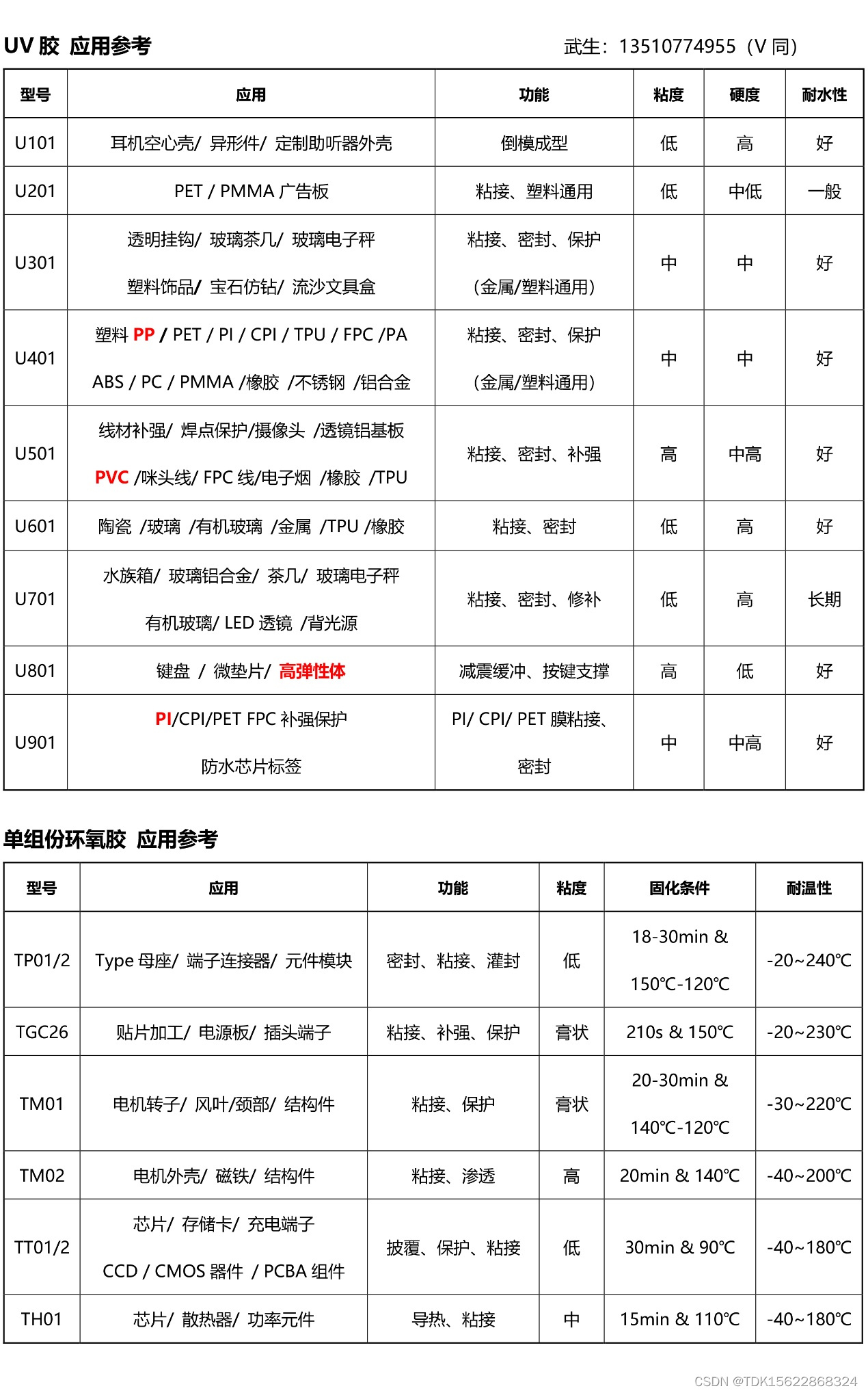
UV胶带和UV胶水的应用场景有哪些不同吗? UV胶带和UV胶水的应用场景确实存在不同之处,以下是详细的比较和归纳: 一:按使用场景来看: UV胶带的应用场景: 包装行业:UV胶带在包装行业中常用于食品包装、药…...

监控员工上网软件有哪些|4款好用的员工上网行为管理软件推荐
在当今数字化办公环境中,确保网络安全、提升工作效率、以及规范员工上网行为成为企业管理的重要组成部分。 为此,一套高效的员工上网行为管理软件显得尤为关键。 本文将为您推荐五款市场上广受好评的员工上网行为管理软件,帮助您有效监控与管…...

【IPython的使用技巧】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
最新AI智能聊天对话问答系统源码(详细图文搭建部署教程)+AI绘画系统(Midjourney),DALL-E3文生图,TTS语音识别输入,文档分析
一、文章前言 随着人工智能技术的持续进步,AI绘画已经发展成为一个日益成熟的领域。越来越多的人开始尝试使用AI绘画软件来创作艺术作品。尽管这些AI绘画软件对绘画领域产生了显著影响,但它们并不会完全取代画师。与传统手绘不同,AI绘画可以…...

项目四 OpenStack身份管理
任务一 理解身份服务 1.1 •Keystone的基本概念 • 认证 ( Authentication ) —— 确认 用户身份的过程,又称身份验证 。 • 凭证 ( Credentials ) —— 又 称凭据,是用于确认用户身份的数据 。 • 令牌 …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
