三体到底是啥?用Python跑一遍就明白了
文章目录
- 拉格朗日方程
- 推导方程组
- 微分方程算法化
- 求解+画图
- 动图绘制
温馨提示,只想看图的画直接跳到最后一节
拉格朗日方程
此前所做的一切三体和太阳系的动画,都是基于牛顿力学的,而且直接对微分进行差分化,从而精度非常感人,用不了几年就得撞一起去。
为了给三体人提供一个更加有价值的推导,这次通过求解拉格朗日方程的数值解来实现。
首先假设三个质点的质量分别为m1,m2,m3m_1, m_2, m_3m1,m2,m3,坐标为x⃗1,x⃗2,x⃗3\vec x_1, \vec x_2, \vec x_3x1,x2,x3,质点速度可以表示为x⃗˙\dot{\vec x}x˙。假设三体在二维平面上运动,则第iii个质点的动能为
Ti=12mi(x˙i2+y˙i2)T_i=\frac{1}{2}m_i(\dot x_i^2+\dot y_i^2) Ti=21mi(x˙i2+y˙i2)
引力势能为−Gmimjrij-G\frac{m_im_j}{r_{ij}}−Grijmimj,其中GGG为万有引力常量,rijr_{ij}rij为质点i,ji,ji,j之间的距离,则系统的拉格朗日量为
L=∑i12mi(x˙i2+y˙i2)−∑i≠jGmimj∥x⃗i−x⃗j∥L=\sum_i\frac{1}{2}m_i(\dot x_i^2+\dot y_i^2)-\sum_{i\not=j}G\frac{m_im_j}{\Vert\vec x_i-\vec x_j\Vert} L=i∑21mi(x˙i2+y˙i2)−i=j∑G∥xi−xj∥mimj
有了拉格朗日量,将其带入拉格朗日方程
ddt∂L∂x˙i−∂L∂xi=0\frac{\text d}{\text dt}\frac{\partial L}{\partial\dot x_i}-\frac{\partial L}{\partial x_i}=0 dtd∂x˙i∂L−∂xi∂L=0
就可以得到拉格朗日方程组。
推导方程组
对于三体系统而言,总计有3个粒子,每个粒子有x,yx,yx,y两个自由度,也就是说最后会得到6组方程。考虑到公式推导过程中可能会出现错误,所以下面采用sympy来进行公式推导。
首先定义符号变量
from sympy import symbols
from sympy.physics.mechanics import dynamicsymbols
m = symbols('m1:4')
x = dynamicsymbols('x1:4')
y = dynamicsymbols('y1:4')
接下来,需要构造系统的拉格朗日量LLL,其实质是系统的动能减去势能,对于上面构建的三体系统而言,动能和势能可分别表示为
计算每个质点的动能和势能。动能是由速度决定的,而速度是由位置对时间的导数决定的。我们可以用 sympy 的 diff 函数来求导:
from sympy import diff
# 此为速度的平方
v2 = [diff(x[i],t)**2 + diff(y[i])**2 for i in range(3)]
T = 0
for i in range(3):T += m[i]*v2[i]/2
势能是由万有引力决定的,而万有引力是由两个质点之间的距离决定的。我们可以用 sympy 的 sqrt 函数来求距离:
from sympy import sqrt,cos
G = symbols('G') # 引力常数
ijs = [(0,1), (0,2),(1,2)]
dij = [sqrt((x[i]-x[j])**2+(y[i]-y[j])**2) for i,j in ijs]
U = 0
for k in range(3):i,j = ijs[k]U -= G*m[i]*m[j]/dij[k]
有了动能和势能,就可以愉快地求拉格朗日量了,有了拉格朗日量,就可以列拉格朗日方程了
L=T−UdLdxi−ddt∂L∂x˙iL = T - U\\ \frac{\text dL}{\text dx_i}-\frac{\text d}{\text dt}\frac{\partial L}{\partial \dot x_i} L=T−UdxidL−dtd∂x˙i∂L
三个粒子的每一个坐标维度,都可以列出一组拉格朗日方程,所以总共有6个拉格朗日方程组
from sympy import solve
L = T - U
eqLag = lambda x : diff(L, x)-diff(diff(L, diff(x, t)), t)
# 拉格朗日方程组
eqs = [eqLag(xi) for xi in x+y]
记xij=xi−xj,yij=yi−yjx_{ij}=x_i-x_j, y_{ij}=y_i-y_jxij=xi−xj,yij=yi−yj,则
−Gm1m2x12(x122+y122)32+−Gm1m3x13(x132+y132)32−m1d2dt2x1=0Gm1m2x12(x122+y122)32+−Gm2m3x23(x232+y232)32−m2d2dt2x2=0Gm1m3x13(x132+y132)32+Gm2m3x23(x232+y232)32−m3d2dt2x3=0−Gm1m2y12(x122+y122)32+−Gm1m3y13(x132+y132)32−m1d2dt2y1=0Gm1m2y12(x122+y122)32+−Gm2m3y23(x232+y232)32−m2d2dt2y2=0Gm1m3y13(x132+y132)32+Gm2m3y23(x232+y232)32−m3d2dt2y3=0\frac{-G m_1 m_2x_{12}}{\left(x_{12}^{2} + y_{12}^{2}\right)^{\frac{3}{2}}} + \frac{-G m_1 m_{3}x_{13}}{\left(x_{13}^{2} + y_{13}^{2}\right)^{\frac{3}{2}}} - m_1 \frac{d^{2}}{d t^2} x_1=0\\ \frac{G m_1 m_2 x_{12}}{\left(x_{12}^{2} + y_{12}^{2}\right)^{\frac{3}{2}}} + \frac{-G m_2 m_{3}x_{23}}{\left(x_{23}^{2} + y_{23}^{2}\right)^{\frac{3}{2}}} - m_2 \frac{d^{2}}{d t^2} x_2=0\\ \frac{G m_1 m_{3} x_{13}}{\left(x_{13}^{2} + y_{13}^{2}\right)^{\frac{3}{2}}} + \frac{G m_2 m_{3} x_{23}}{\left(x_{23}^{2} + y_{23}^{2}\right)^{\frac{3}{2}}} - m_{3} \frac{d^{2}}{d t^2} x_{3}=0\\ \frac{-G m_1 m_2 y_{12}}{\left(x_{12}^{2} + y_{12}^{2}\right)^{\frac{3}{2}}} + \frac{-G m_1 m_{3} y_{13}}{\left(x_{13}^{2} + y_{13}^{2}\right)^{\frac{3}{2}}} - m_1 \frac{d^{2}}{d t^2} y_1=0\\ \frac{G m_1 m_2 y_{12}}{\left(x_{12}^{2} + y_{12}^{2}\right)^{\frac{3}{2}}} + \frac{-G m_2 m_{3}y_{23}}{\left(x_{23}^{2} + y_{23}^{2}\right)^{\frac{3}{2}}} - m_2 \frac{d^{2}}{d t^2} y_2=0\\ \frac{G m_1 m_{3} y_{13}}{\left(x_{13}^{2} + y_{13}^{2}\right)^{\frac{3}{2}}} + \frac{G m_2 m_{3} y_{23}}{\left(x_{23}^{2} + y_{23}^{2}\right)^{\frac{3}{2}}} - m_{3} \frac{d^{2}}{d t^2} y_{3}=0\\ (x122+y122)23−Gm1m2x12+(x132+y132)23−Gm1m3x13−m1dt2d2x1=0(x122+y122)23Gm1m2x12+(x232+y232)23−Gm2m3x23−m2dt2d2x2=0(x132+y132)23Gm1m3x13+(x232+y232)23Gm2m3x23−m3dt2d2x3=0(x122+y122)23−Gm1m2y12+(x132+y132)23−Gm1m3y13−m1dt2d2y1=0(x122+y122)23Gm1m2y12+(x232+y232)23−Gm2m3y23−m2dt2d2y2=0(x132+y132)23Gm1m3y13+(x232+y232)23Gm2m3y23−m3dt2d2y3=0
微分方程算法化
接下来就要调用Python的odeint来计算这个微分方程组的数值解,odeint的调用方法大致为odeint(func, y, t, args),其中func是一个函数,这个函数必须为func(y,t,...),且返回值为dydt\frac{\text dy}{\text dt}dtdy。
为此,需要将上述方程组再行拆分,以消去其中的二次导数,以x1x_1x1为例,令u1=dx1dtu_1=\frac{\text dx_1}{\text dt}u1=dtdx1,则此方程变为方程组
x˙1(t)=u1(t)u˙1(t)=−Gm1m2x12(x122+y122)32+−Gm1m3x13(x132+y132)32\begin{aligned} \dot x_1(t)&=u_1(t)\\ \dot u_1(t)&= \frac{-G m_1 m_2x_{12}}{\left(x_{12}^{2} + y_{12}^{2}\right)^{\frac{3}{2}}} + \frac{-G m_1 m_{3}x_{13}}{\left(x_{13}^{2} + y_{13}^{2}\right)^{\frac{3}{2}}}\\ \end{aligned} x˙1(t)u˙1(t)=u1(t)=(x122+y122)23−Gm1m2x12+(x132+y132)23−Gm1m3x13
由于三体系统中有3个粒子,共6个独立变量,所以要列12个方程。记u(t)=textdxdt,v(t)=dydtu(t)=\frac{text dx}{\text dt}, v(t)=\frac{\text dy}{\text dt}u(t)=dttextdx,v(t)=dtdy,则odeint输入的y的形式为
[x1,x2,x3,y1,y2,y3,u1,u2,u3,v1,v2,v3][x_1, x_2, x_3, y_1, y_2, y_3, u_1, u_2, u_3, v_1, v_2, v_3] [x1,x2,x3,y1,y2,y3,u1,u2,u3,v1,v2,v3]
从而func的具体形式为
import numpy as np
dxy = lambda x,y : np.sqrt(x**2+y**2)**(3/2)
def triSys(Y, t, m, G):jk = [(1,2),(0,2),(0,1)]x,y = Y[:3], Y[3:6]u,v = Y[6:9], Y[9:]du, dv = [], []for i in range(3):j, k = jk[i]xji, xki = x[j]-x[i], x[k]-x[i]yji, yki = y[j]-y[i], y[k]-y[i]dji, dki = dxy(xji, yji), dxy(yji, yki)mji, mki = G*m[i]*m[j], G*m[i]*m[k]du.append(mji*xji/dji + mki*xki/dki)dv.append(mji*yji/dji + mki*yki/dki)dydt = [*u, *v, *du, *dv]return dydt
求解+画图
接下来就是见证奇迹的时刻,首先创建一个随机的起点,作为三体运动的初值,然后带入开整就完事儿了
from scipy.integrate import odeint
np.random.seed(42)
y0 = np.random.rand(12)
m = np.random.rand(3)
t = np.linspace(0, 20, 1001)
sol = odeint(triSys, y0, t, args=(m, 1))
然后绘制一下这三颗星的轨迹
import matplotlib.pyplot as plt
plt.plot(sol[:,0], sol[:,3])
plt.plot(sol[:,1], sol[:,4])
plt.plot(sol[:,2], sol[:,5])
plt.show()

光是看这个轨迹就十分惊险了有木有。
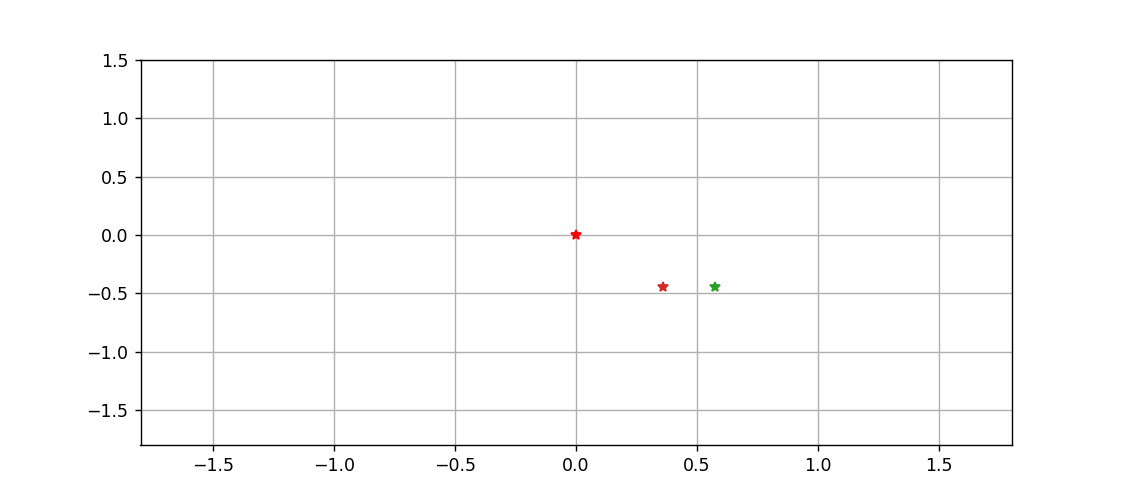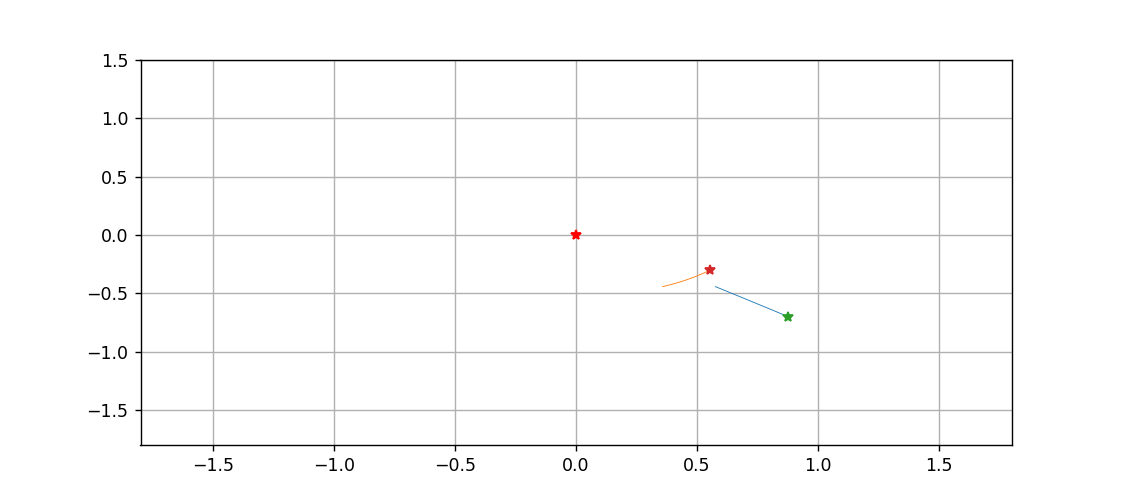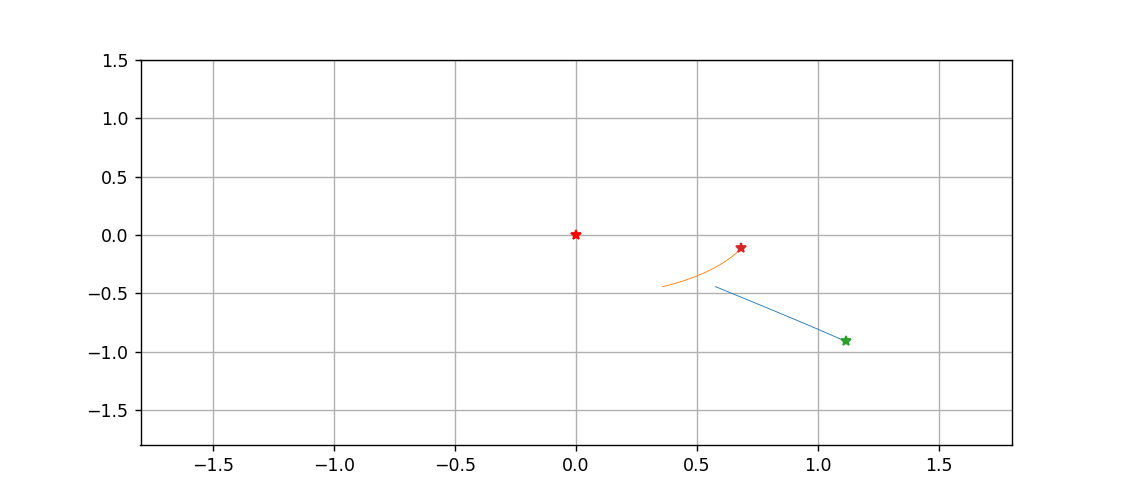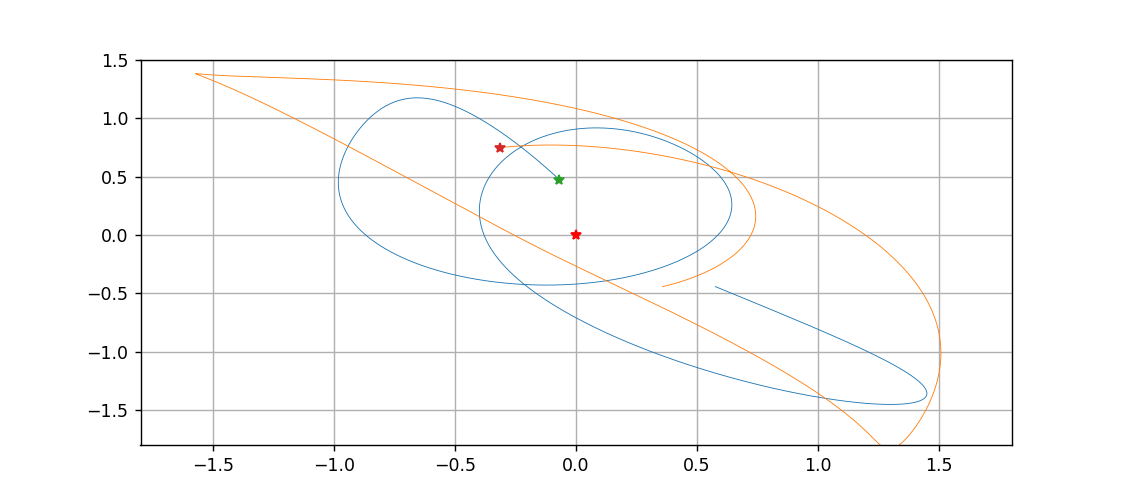
如果把其中的第一颗星作为坐标原点,那么另外两颗星的轨迹大致为
plt.plot(sol[:,1]-sol[:,0], sol[:,4]-sol[:,3])
plt.plot(sol[:,2]-sol[:,0], sol[:,5]-sol[:,3])
plt.scatter([0],[0], c='g', marker='*')
plt.show()
结果为

动图绘制
最后,以中间这颗星为原点,绘制一下另外两颗星运动的动态过程
import matplotlib.animation as animation fig = plt.figure(figsize=(9,4))
ax = fig.add_subplot(xlim=(-1.8,1.8),ylim=(-1.8,1.5))
ax.grid()traces = [ax.plot([],[],'-',lw=0.5)[0] for _ in range(2)]
pts = [ax.plot([],[] ,marker='*')[0] for _ in range(2)]
ax.plot([0],[0], marker="*", c='r')X1 = sol[:,1]-sol[:,0]
Y1 = sol[:,4]-sol[:,3]
X2 = sol[:,2]-sol[:,0]
Y2 = sol[:,5]-sol[:,3]def animate(n):traces[0].set_data(X1[:n], Y1[:n])traces[1].set_data(X2[:n], Y2[:n])pts[0].set_data([X1[n], Y1[n]])pts[1].set_data([X2[n], Y2[n]])return traces + ptsani = animation.FuncAnimation(fig, animate, range(1000), interval=10, blit=True)
ani.save('tri.gif')
相关文章:

三体到底是啥?用Python跑一遍就明白了
文章目录拉格朗日方程推导方程组微分方程算法化求解画图动图绘制温馨提示,只想看图的画直接跳到最后一节拉格朗日方程 此前所做的一切三体和太阳系的动画,都是基于牛顿力学的,而且直接对微分进行差分化,从而精度非常感人…...

Golang-Hello world
目录 安装 Go(如果尚未安装) 编写Hello world 使用Golang的外部包 自动下载需要的外部包...

this指针C++
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章 🔥座右铭:“不要等到什么都没有了,才下定决心去做” …...

SpringBoot+WebSocket实时监控异常
# 写在前面此异常非彼异常,标题所说的异常是业务上的异常。最近做了一个需求,消防的设备巡检,如果巡检发现异常,通过手机端提交,后台的实时监控页面实时获取到该设备的信息及位置,然后安排员工去处理。因为…...
Baumer工业相机堡盟相机如何使用自动曝光功能(自动曝光优点和行业应用)(C++)
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

HTML、CSS学习笔记7(移动适配:rem、less)
一、移动适配 rem:目前多数企业在用的解决方案vw / vh:未来的解决方案 1.rem(单位) 1.1使用rem单位设置尺寸 px单位或百分比布局可以实现吗? ————不可以 网页的根字号——HTML标签 1.2.rem移动适配 写法&#x…...
STM32感应开关盖垃圾桶
目录 项目需求 项目框图 编辑 硬件清单 sg90舵机介绍及实战 sg90舵机介绍 角度控制 SG90舵机编程实现 超声波传感器介绍及实战 超声波传感器介绍 超声波编程实战 项目设计及实现 项目需求 检测靠近时,垃圾桶自动开盖并伴随滴一声,2秒后关盖…...

进程跟线程的区别
进程跟线程的区别 文章目录进程跟线程的区别前言一.什么线程二.线程与进程的联系三.线程与进程有什么不同前言 现代所有计算机都能同时做几件事情,当一个用户程序正在运行时,计算机还能同时读取磁盘,并向屏幕打印输出正文.在一个多道操作程序中,cpu由一道程序向另外一道程的切…...

[ICLR 2016] Unsupervised representation learning with DCGANs
目录 IntroductionModel ArchitectureReferencesIntroduction 作者提出了用 CNN 搭建 GAN,使得 GAN 训练更加稳定的一系列准则,并将满足这些设计理念的模型称为 DCGANs (Deep Convolutional GANs). 此外,作者将 trained discriminators 用于图像分类任务,相比于其他无监督算…...

QT编程从入门到精通之十五:“第五章:Qt GUI应用程序设计”之“5.1 UI文件设计与运行机制”之“5.1.2 项目管理文件”
目录 第五章:Qt GUI应用程序设计 5.1 UI文件设计与运行机制 5.1.2 项目管理文件 第五章:Qt GUI应用程序设计 在“Qt 程序创建基础”上,本章将继续深入地介绍Qt Creator设计GUI应用程序的方法...

基于Three.js和MindAR实现的网页端WebAR人脸识别追踪功能的京剧换脸Demo(含源码)
前言 近段时间一直在玩MindAR的功能,之前一直在弄图片识别追踪的功能,发现其强大的功能还有脸部识别和追踪的功能,就基于其面部网格的例子修改了一个国粹京剧的换脸程序。如果你不了解MindAR的环境配置可以先参考这篇文章:基于Mi…...

动态规划思路
拉勾教育版权所有:https://kaiwu.lagou.com/course/courseInfo.htm?courseId3 动态规划思路 1.最优子结构 2.重复计算子机构 3.依靠递归,层层向上传值,所以编程时初始化子结构很重要 动态规划步骤 1.判断动态规划的类型 1.线性规划 >&…...

HTTPS关键词语解释和简单通讯流程
1、 什么是HTTPS HTTPS是基于HTTP的上层添加了一个叫做TLS的安全层,对数据的加密等操作都是在这个安全层中进行处理的,其底层还是应用的HTTP。 2、 什么是对称加密; 加密和解密都是用同一个秘钥 3、 什么是非对称加密; 加密和…...

“前端开发中的三种定时任务及其应用“
前端定时任务是指在一定时间间隔内,自动执行指定的操作或函数。在前端开发中,定时任务被广泛应用于诸如数据更新、定时提醒、定时刷新页面等方面。在本文中,我们将介绍前端中常见的三种定时任务,分别是 setTimeout、setInterval 和…...
| 机考必刷)
华为OD机试题 - 猜字谜(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:猜字谜题目输入输出描述备注示例一输入输出示例二输入输出思路C…...

python@pyside样式化
文章目录refWidget类创建样式化文件qss引用样式并启动应用ref Styling the Widgets Application - Qt for PythonQt Style Sheets Reference | Qt Widgets 5.15.12 Widget类创建 创建一个简单界面(菜单主要内容)它们是水平布局 主要内容包括一段文本和一个按钮,它们是垂直布…...
)
C++经典15道面试题目(文末含大题)
今天给大家找了几个C面试里很有可能被问的哦,赶紧收藏下来去背!!! 目录 1)C中有malloc/free,为什么还需要new/delete? 2)C中explicit关键字的作用? 3)C中static关键字的作用&a…...

自动计算30天内的股价最高价源代码
我可以回答这个问题。您可以使用以下代码来计算30天内股价的最高价: 复制 import pandas as pd import yfinance as yf # 设置股票代码和日期范围 symbol "AAPL" start_date "2021-01-01" end_date "2021-06-30" # 获取股票…...

国外SEO升级攻略!一看就懂!
SEO是搜索引擎优化的缩写,它是指通过优化网站内容和结构,提升网站在搜索引擎中的排名,从而获得更多的有价值的流量。 而关键词研究和选择是SEO优化中最基础也是最关键的环节,它决定了网站将面向哪些用户、哪些关键词和词组将被优…...
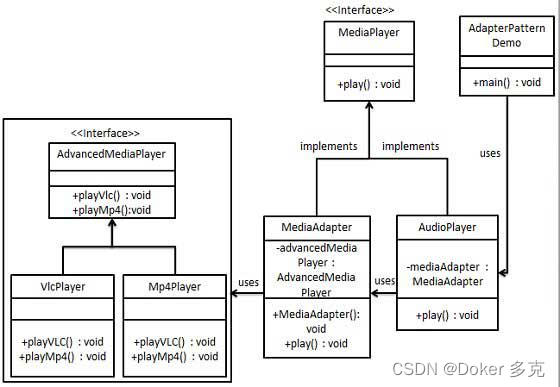
设计模式—适配器模式
适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁。这种类型的设计模式属于结构型模式,它结合了两个独立接口的功能。这种模式涉及到一个单一的类,该类负责加入独立的或不兼容的接口功能。举个真实的例子,…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
