吴恩达机器学习 第二课 week2 多分类问题
目录
01 学习目标
02 实现工具
03 概念与原理
04 应用示例
05 总结
01 学习目标
(1)理解二分类与多分类的原理区别
(2)掌握简单多分类问题的神经网络实现方法
(3)理解多分类问题算法中的激活函数与损失函数原理
02 实现工具
(1)代码运行环境
Python语言,Jupyter notebook平台
(2)所需模块
numpy,matplotlib,tensorflow,lab_utils_multiclass_TF,logging
03 概念与原理
(1)二分类&多分类
二分类将输入数据划分为两个不同类别,目标变量为一维(0或1)。比如:判断一封电子邮件是否为垃圾邮件(是/否)、判断一个用户是否会点击某个广告或链接(会/不会)等。
多分类将输入数据划分为三个及以上不同类别,目标变量为一维或更高维。比如:图像识别、文本分类等。
二分类与多分类都是分类问题,本质上都是经过逻辑分析进行处理。相较二分类的“一对一(0&1)”逻辑,多分类多了一层逻辑,其逻辑处理有“一对一(0或1)”和“一对多(0&1/2/3/4…)”两种策略。如下图所示:

图1 “一对一”策略

图2 “一对多”策略
由图1和2可知,假设目标有n类,“一对一”策略需要n×(n-1)次分类,而“一对多”策略仅需要n次分类。
(2)神经网络中的激活函数 & 归一化指数函数(SoftMax函数)
激活函数负责将神经元的输入映射到输出端,位于隐藏层的神经元内。作用:引入非线性以处理现实复杂问题。
SoftMax函数负责处理输出层神经元的输出结果,位于模型编译过程中、损失函数内。作用:将输出层数值处理为 [0,1]范围内的概率分布,用于预测。
(3)SoftMax函数及其损失函数的数学原理
对于输出结果向量,SoftMax函数:
对于SoftMax处理后的数值,采用交叉熵损失函数:
成本函数:
然而,实际项目中可能遇到比较大的数值,SoftMax函数第1步会先进行指数计算(即e^x),这往往造成内存溢出无法计算。因此,可对SoftMax函数及其损失函数进行算法优化:
本质为取进行归一化预处理,具体推导过程如下:

优化后的SoftMax函数如下:
优化后的第k类的损失函数为:
式中,,k为目标值(类别),即y=k,总共有n类。
04 应用示例
(1)示例描述
采用sklearn库中的make_blobs函数随机生成4类共2000个数据点,然后基于这4类数据,采用人工神经网络对其进行分类并可视化。
(2)代码实现
第1步,导入所需模块:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib widget
from sklearn.datasets import make_blobs
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
np.set_printoptions(precision=2)
from lab_utils_multiclass_TF import *
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)第2步,生成数据:
centers = [[-5, 2], [-2, -2], [1, 2], [5, -2]] # 4个类中心
X_train, y_train = make_blobs(n_samples=2000, centers=centers, cluster_std=1.0,random_state=30)第3步,定义框架、编译模型、训练模型:
model = Sequential([ Dense(25, activation = 'relu'),Dense(15, activation = 'relu'),Dense(4, activation = 'linear') # < softmax activation here]
)
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),optimizer=tf.keras.optimizers.Adam(0.001),
)model.fit(X_train,y_train,epochs=100
)第4步,结果显示:
plt_cat_mc(X_train, y_train, model, 4)运行以上代码,结果如下:
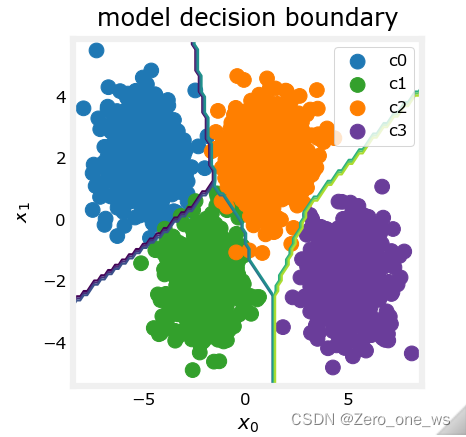
05 总结
(1)多分类的本质是二分类,基本原理是逻辑回归。
(2)采用Softmax需在损失函数中定义,并需输出层以激活函数linear配合。
(3)二分类输出层的神经元个数为1,多分类问题输出层神经元个数为类别个数,若类数未知则可通过试算确定。
相关文章:

吴恩达机器学习 第二课 week2 多分类问题
目录 01 学习目标 02 实现工具 03 概念与原理 04 应用示例 05 总结 01 学习目标 (1)理解二分类与多分类的原理区别 (2)掌握简单多分类问题的神经网络实现方法 (3)理解多分类问题算法中的激活函数与损失…...

112、路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点 是指没有子节点…...

Vue 封装组件之Input框
封装Input组件:MyInput.vue <template><div class"base-input-wraper"><el-inputv-bind"$attrs"v-on"$listeners"class"e-input":style"inputStyle":value"value":size"size"input&quo…...

一段代码让你了解Java中的抽象
我们先来看一道题! 计算几何对象的面积之和)编写一个方法,该方法用于计算数组中所有几何对象的面积之和。该方法的签名是: public static double sumArea(GeometricObject[] a) 编写一个测试程序,该程序创建一个包含四…...
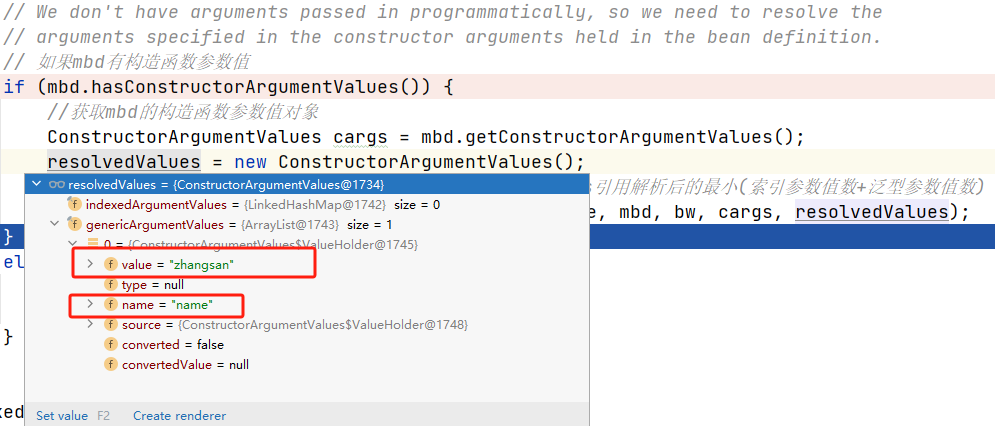
Sping源码(九)—— Bean的初始化(非懒加载)— Bean的创建方式(factoryMethod)
序言 前面文章介绍了在Spring中多种创建Bean实例的方式,包括采用FactoryBean的方式创建对象、使用反射创建对象、自定义BeanFactoryPostProcessor。 这篇文章继续介绍Spring中创建Bean的形式之一——factoryMethod。方法用的不多,感兴趣可以当扩展了解。…...

绝对全网首发,利用Disruptor EventHandler实现在多线程下顺序执行任务
disruptor有两种任务处理器,一个是EventHandler ,另一个是WorkHandler. EventHandler可以彼此独立消费同一个队列中的任务,WorkHandler可以共同竞争消费同一个队列中的任务。也就是说,假设任务队列中有a、b、c、d三个事件,eventHa…...

单例设计模式双重检查的作用
先看双重校验锁的写法 public class Singleton {/*volatile 修饰,singleton new Singleton() 可以拆解为3步:1、分配对象内存(给singleton分配内存)2、调用构造器方法,执行初始化(调用 Singleton 的构造函数来初始化成员变量&am…...
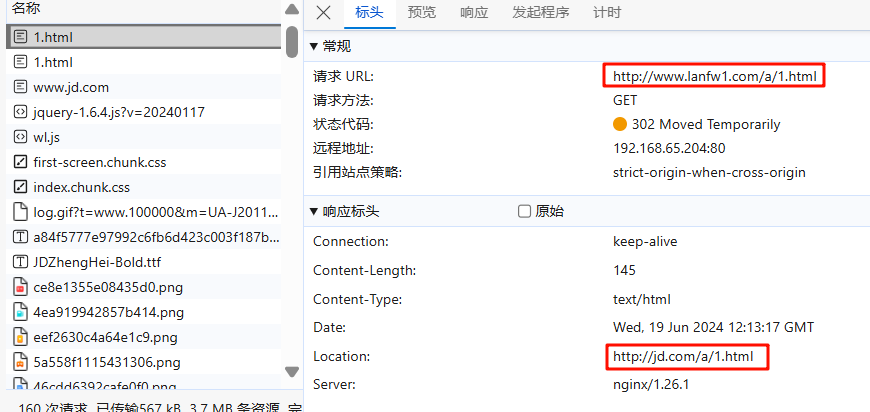
NGINX_十二 nginx 地址重写 rewrite
十二 nginx 地址重写 rewrite 1 什么是Rewrite Rewrite对称URL Rewrite,即URL重写,就是把传入Web的请求重定向到其他URL的过程。URL Rewrite最常见的应用是URL伪静态化,是将动态页面显示为静态页面方式的一种技术。比如 http://www.123.com…...
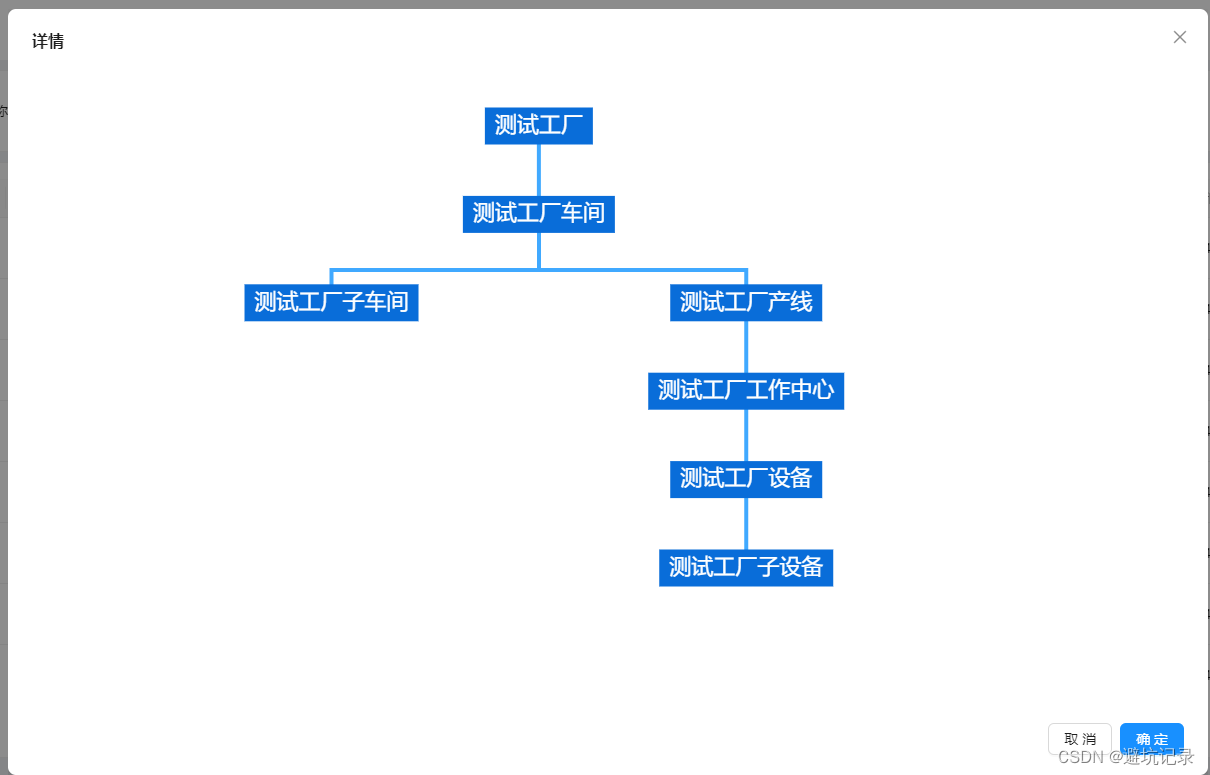
react用ECharts实现组织架构图
找到ECharts中路径图。 然后开始爆改。 <div id{org- name} style{{ width: 100%, height: 650, display: flex, justifyContent: center }}></div> // data的数据格式 interface ChartData {name: string;value: number;children: ChartData[]; } const treeDep…...

坚持刷题|合并有序链表
文章目录 题目思考代码实现迭代递归 扩展实现k个有序链表合并方法一方法二 PriorityQueue基本操作Java示例注意事项 Hello,大家好,我是阿月。坚持刷题,老年痴呆追不上我,消失了一段时间,我又回来刷题啦,今天…...
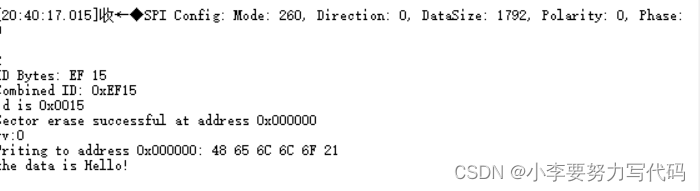
SPI协议——对外部SPI Flash操作
目录 1. W25Q32JVSSIQ背景知识 1.1 64个可擦除块 1.2 1024个扇区(每个块有16个扇区) 1.3 页 1. W25Q32JVSSIQ背景知识 W25Q32JV阵列被组织成16,384个可编程页,每页有256字节。一次最多可以编程256个字节。页面可分为16组(4KB扇区清除&…...

kotlin类型检测与类型转换
一、is与!is操作符 1、使用 is 操作符或其否定形式 !is 在运行时检测对象是否符合给定类型。 fun main() {var a "1"if(a is String) {println("a是字符串类型:${a.length}")}// 或val b a is Stringprintln(b) } 二、"不安全的"转换操作符…...

【JDBC】Oracle数据库连接问题记录
Failed to load driver class oracle.jdbc.driver.OracleDriver in either of HikariConfig class oracle驱动包未正确加载,可以先尝试使用下面方式加载检查类是否存在,如果不存在需要手动下载odbc包 try {Class.forName("oracle.jdbc.driver.Ora…...

leetcode45 跳跃游戏II
题目 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返回到达 nums[n - 1]…...

【数学】什么是方法矩估计?和最大似然估计是什么关系?
背景 方法矩估计(Method of Moments Estimation)和最大似然估计(Maximum Likelihood Estimation, MLE)是两种常用的参数估计方法。方法矩估计基于样本矩与总体矩的关系,通过样本数据计算样本矩来估计总体参数。最大似…...

C++初学者指南第一步---10.内存(基础)
C初学者指南第一步—10.内存(基础) 文章目录 C初学者指南第一步---10.内存(基础)1.内存模型1.1 纸上谈兵:C的抽象内存模型1.2 实践:内存的实际处理 2. 自动存储3.动态存储:std::vector3.1 动态内…...

扩散模型详细推导过程——编码与解码
符号表 符号含义 x ( i ) z 0 ( i ) \boldsymbol{x}^{(i)}\boldsymbol{z}_0^{(i)} x(i)z0(i)第 i i i个训练数据,其为长度为 d d d的向量 z t ( i ) \boldsymbol{z}_t^{(i)} zt(i)第 i i i个训练数据在第 t t t时刻的加噪版本 ϵ t ( i ) \boldsymbol{\epsilo…...

js如何实现开屏弹窗
开屏弹窗是什么,其实就是第一次登录后进入页面给你的一种公告提示,此后再回到当前这个页面时弹窗是不会再出现的。也就是说这个弹窗只会出现一次。 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>…...

C#——文件读取Directory类详情
文件读取Directory类 Durectory提供了目录以及子目录进行创建移动和列举操作方法 Directory和Directorylnfo类(主要操作文件目录属性列如文件是否隐藏的 或者只读等这些属性) Directory对目录进行复制、移动、重命名、创建和删除等操作DirectoryInfo用于对目录属性执行操作 …...

Ruby on Rails Post项目设置网站初始界面
在构建了Ruby的Web服务器后,第三步就可以去掉框架的官方页面,设置自己的网页初始页了。 Linux系统安装Ruby语言-CSDN博客 、在Ubuntu中创建Ruby on Rails项目并搭建数据库-CSDN博客、 Ruby语言建立Web服务器-CSDN博客 了解Ruby onRails项目中的主要文件…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
