【数学】什么是方法矩估计?和最大似然估计是什么关系?
背景
方法矩估计(Method of Moments Estimation)和最大似然估计(Maximum Likelihood Estimation, MLE)是两种常用的参数估计方法。方法矩估计基于样本矩与总体矩的关系,通过样本数据计算样本矩来估计总体参数。最大似然估计基于最大化样本数据的联合概率密度函数,通过寻找参数值使得样本数据出现的概率最大来估计参数。
公式
方法矩估计
方法矩估计基于以下公式:
- 样本矩: M k = 1 n ∑ i = 1 n X i k M_k = \frac{1}{n} \sum_{i=1}^{n} X_i^k Mk=n1∑i=1nXik
- 总体矩: E ( X k ) = μ k E(X^k) = \mu_k E(Xk)=μk
通过设定样本矩等于总体矩,可以解出参数估计值。
最大似然估计
最大似然估计基于以下公式:
- 似然函数: L ( θ ) = ∏ i = 1 n f ( X i ; θ ) L(\theta) = \prod_{i=1}^{n} f(X_i; \theta) L(θ)=∏i=1nf(Xi;θ)
- 对数似然函数: ln L ( θ ) = ∑ i = 1 n ln f ( X i ; θ ) \ln L(\theta) = \sum_{i=1}^{n} \ln f(X_i; \theta) lnL(θ)=∑i=1nlnf(Xi;θ)
通过最大化对数似然函数来求解参数估计值。
示例题目
示例 1:正态分布参数估计
假设样本数据来自一个均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2的正态分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2),我们要估计 μ \mu μ和 σ 2 \sigma^2 σ2。
详细讲解
方法矩估计
-
样本矩计算:
- 一阶样本矩: M 1 = 1 n ∑ i = 1 n X i M_1 = \frac{1}{n} \sum_{i=1}^{n} X_i M1=n1∑i=1nXi
- 二阶样本矩: M 2 = 1 n ∑ i = 1 n X i 2 M_2 = \frac{1}{n} \sum_{i=1}^{n} X_i^2 M2=n1∑i=1nXi2
-
总体矩关系:
- 一阶总体矩: E ( X ) = μ E(X) = \mu E(X)=μ
- 二阶总体矩: E ( X 2 ) = μ 2 + σ 2 E(X^2) = \mu^2 + \sigma^2 E(X2)=μ2+σ2
-
通过样本矩等于总体矩,得到:
μ ^ = M 1 = 1 n ∑ i = 1 n X i \hat{\mu} = M_1 = \frac{1}{n} \sum_{i=1}^{n} X_i μ^=M1=n1i=1∑nXi
σ ^ 2 = M 2 − μ ^ 2 \hat{\sigma}^2 = M_2 - \hat{\mu}^2 σ^2=M2−μ^2
最大似然估计
-
似然函数:
L ( μ , σ 2 ) = ∏ i = 1 n 1 2 π σ 2 exp ( − ( X i − μ ) 2 2 σ 2 ) L(\mu, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(X_i - \mu)^2}{2\sigma^2} \right) L(μ,σ2)=i=1∏n2πσ21exp(−2σ2(Xi−μ)2) -
对数似然函数:
ln L ( μ , σ 2 ) = − n 2 ln ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( X i − μ ) 2 \ln L(\mu, \sigma^2) = -\frac{n}{2} \ln(2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^{n} (X_i - \mu)^2 lnL(μ,σ2)=−2nln(2πσ2)−2σ21i=1∑n(Xi−μ)2 -
对 μ \mu μ和 σ 2 \sigma^2 σ2求导并设为0,解得:
μ ^ = 1 n ∑ i = 1 n X i \hat{\mu} = \frac{1}{n} \sum_{i=1}^{n} X_i μ^=n1i=1∑nXi
σ ^ 2 = 1 n ∑ i = 1 n ( X i − μ ^ ) 2 \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \hat{\mu})^2 σ^2=n1i=1∑n(Xi−μ^)2
Python代码求解
import numpy as np# 生成样本数据
np.random.seed(0)
data = np.random.normal(loc=5, scale=2, size=100)# 方法矩估计
mu_mom = np.mean(data)
sigma2_mom = np.mean(data**2) - mu_mom**2# 最大似然估计
mu_mle = np.mean(data)
sigma2_mle = np.var(data, ddof=0)print("方法矩估计:")
print(f"mu = {mu_mom}, sigma^2 = {sigma2_mom}")print("最大似然估计:")
print(f"mu = {mu_mle}, sigma^2 = {sigma2_mle}")
实际生活中的例子
在金融领域中,投资组合的收益通常被假设为正态分布。为了估计未来收益的均值和波动率,金融分析师可以使用历史收益数据来进行参数估计。通过方法矩估计或最大似然估计,可以得出投资组合的均值收益和方差,从而指导投资决策。
方法矩估计与最大似然估计的关系与优缺点
两种方法各有优缺点:
- 方法矩估计通常计算简单,易于理解,但在有限样本量下估计量的效率较低。
- 最大似然估计在大样本量下具有一致性和渐近正态性,估计量更有效,但计算复杂,尤其是对于复杂模型。
选择哪种方法更好取决于具体问题和数据特点。一般情况下,最大似然估计更受欢迎,因为它在大样本下具有良好的统计性质。
相关文章:

【数学】什么是方法矩估计?和最大似然估计是什么关系?
背景 方法矩估计(Method of Moments Estimation)和最大似然估计(Maximum Likelihood Estimation, MLE)是两种常用的参数估计方法。方法矩估计基于样本矩与总体矩的关系,通过样本数据计算样本矩来估计总体参数。最大似…...

C++初学者指南第一步---10.内存(基础)
C初学者指南第一步—10.内存(基础) 文章目录 C初学者指南第一步---10.内存(基础)1.内存模型1.1 纸上谈兵:C的抽象内存模型1.2 实践:内存的实际处理 2. 自动存储3.动态存储:std::vector3.1 动态内…...

扩散模型详细推导过程——编码与解码
符号表 符号含义 x ( i ) z 0 ( i ) \boldsymbol{x}^{(i)}\boldsymbol{z}_0^{(i)} x(i)z0(i)第 i i i个训练数据,其为长度为 d d d的向量 z t ( i ) \boldsymbol{z}_t^{(i)} zt(i)第 i i i个训练数据在第 t t t时刻的加噪版本 ϵ t ( i ) \boldsymbol{\epsilo…...

js如何实现开屏弹窗
开屏弹窗是什么,其实就是第一次登录后进入页面给你的一种公告提示,此后再回到当前这个页面时弹窗是不会再出现的。也就是说这个弹窗只会出现一次。 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>…...

C#——文件读取Directory类详情
文件读取Directory类 Durectory提供了目录以及子目录进行创建移动和列举操作方法 Directory和Directorylnfo类(主要操作文件目录属性列如文件是否隐藏的 或者只读等这些属性) Directory对目录进行复制、移动、重命名、创建和删除等操作DirectoryInfo用于对目录属性执行操作 …...

Ruby on Rails Post项目设置网站初始界面
在构建了Ruby的Web服务器后,第三步就可以去掉框架的官方页面,设置自己的网页初始页了。 Linux系统安装Ruby语言-CSDN博客 、在Ubuntu中创建Ruby on Rails项目并搭建数据库-CSDN博客、 Ruby语言建立Web服务器-CSDN博客 了解Ruby onRails项目中的主要文件…...

03-QTWebEngine中使用qtvirtualkeyboard
qt提供了 virtualKeyboard 虚拟键盘模块,只需要在在main函数中最开始加入这样一句就可以了 qputenv("QT_IM_MODULE", QByteArray("qtvirtualkeyboard")); 但是在使用的时候遇到了一些问题: 1、中文输入的时候没有输入提示 Qvirt…...
)
leetcode3无重复字符的最长字串(重点讲滑动窗口)
本文主要讲解无重复字符的最长字串的要点与细节,根据步骤一步步走更方便理解 c与java代码如下,末尾 具体要点: 1. 区分一下子串和子序列 子串:要求元素在母串中是连续地出现 子序列:不要求连续 2. 题目中有两个核心…...
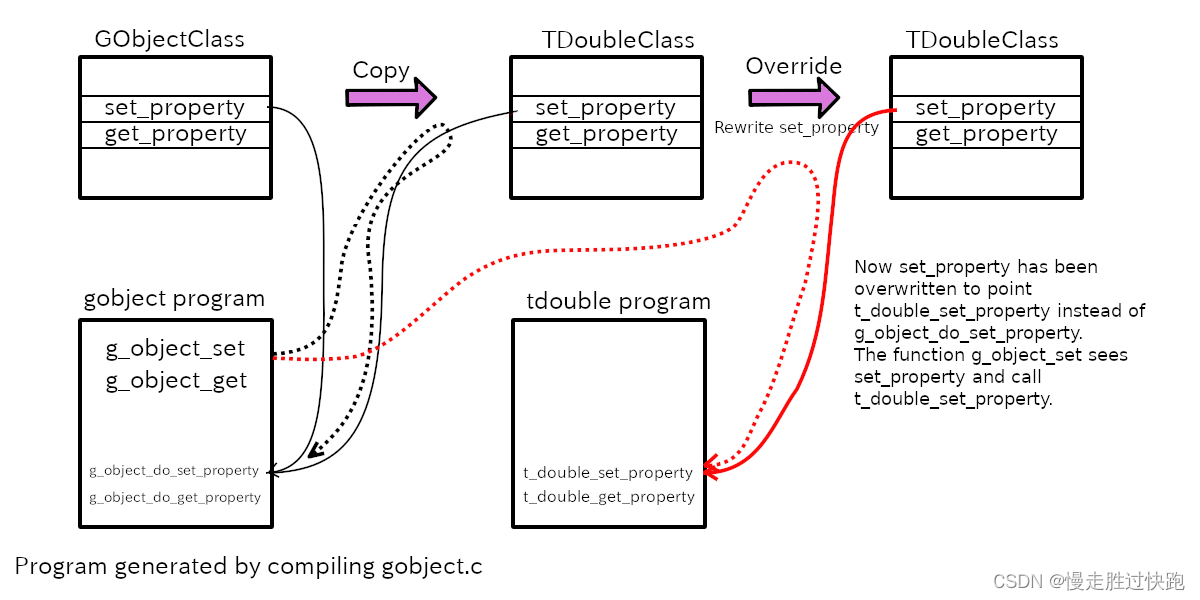
Gobject tutorial 八
The GObject base class Object memory management Gobject的内存管理相关的API很复杂,但其目标是提供一个基于引用计数的灵活的内存管理模式。 下面我们来介绍一下,与管理引用计数相关的函数。 Reference Count 函数g_object_ref和g_object_unref的…...

DDMA信号处理以及数据处理的流程---cfar检测
Hello,大家好,我是Xiaojie,好久不见,欢迎大家能够和Xiaojie一起学习毫米波雷达知识,Xiaojie准备连载一个系列的文章—DDMA信号处理以及数据处理的流程,本系列文章将从目标生成、信号仿真、测距、测速、cfar检测、测角、目标聚类、目标跟踪这几个模块逐步介绍,这个系列的…...
【机器学习】从理论到实践:决策树算法在机器学习中的应用与实现
📝个人主页:哈__ 期待您的关注 目录 📕引言 ⛓决策树的基本原理 1. 决策树的结构 2. 信息增益 熵的计算公式 信息增益的计算公式 3. 基尼指数 4. 决策树的构建 🤖决策树的代码实现 1. 数据准备 2. 决策树模型训练 3.…...

Zookeeper 集群节点故障剔除、切换、恢复原理
Zookeeper 集群节点故障剔除、切换、恢复原理 zookeeper 集群节点故障时,如何剔除节点,如果为领导节点如何处理,如何进行故障恢 复的,实现原理? 在 Zookeeper 集群中,当节点故障时,集群需要自动剔除故障节点并进行故障恢复,确保集群的高 可用性和一致性。具体来说,…...

解决帝国cms栏目管理拼音乱码的问题
帝国CMS7.5版本utf-8版网站后台增加栏目生成乱码的问题怎么解决 1、需要改一个函数,并且增加一个处理文件,方法如下: 修改e/class/connect.php文件,找到ReturnPinyinFun函数,如未修改文件在4533-4547行,将…...

Git快速入门
一 快速使用 1.1 初始化 什么是版本库呢?版本库又名仓库,可以简单理解成一个目录,这个目录里面的所有文件都可以被Git管理起来,每个文件的修改、删除,Git都能跟踪,以便任何时刻都可以追踪历史࿰…...

【18.0】JavaScript---事件案例
【18.0】JavaScript—事件案例 【一】开关灯事件 【介绍】设置一个按钮,按下按钮触发事件,来回切换圆形图片的颜色 【分析】 图片设置:设置成圆形的图片背景颜色:设置红绿两个颜色,来回切换按钮设置:点击…...
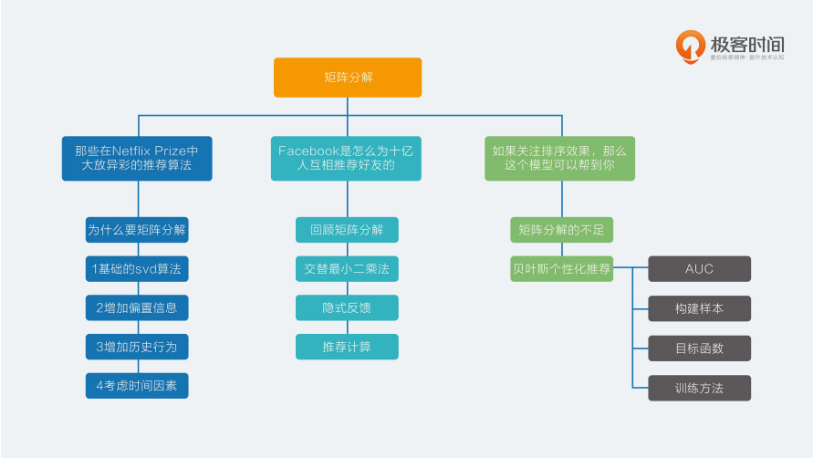
推荐系统三十六式学习笔记:原理篇.矩阵分解12|如果关注排序效果,那么这个模型可以帮到你
目录 矩阵分解的不足贝叶斯个性化排序AUC构造样本目标函数训练方法 总结 矩阵分解在推荐系统中的地位非常崇高。它既有协同过滤的血统,又有机器学习的基因,可以说是非常优秀了;但即便如此,传统的矩阵分解无论是在处理显式反馈&…...

Kafka之ISR机制的理解
文章目录 Kafka的基本概念什么是ISRISR的维护机制ISR的作用ISR相关配置参数同步过程示例代码总结 Kafka中的ISR(In-Sync Replicas同步副本)机制是确保数据高可用性和一致性的核心组件。 Kafka的基本概念 在Kafka中,数据被组织成主题…...
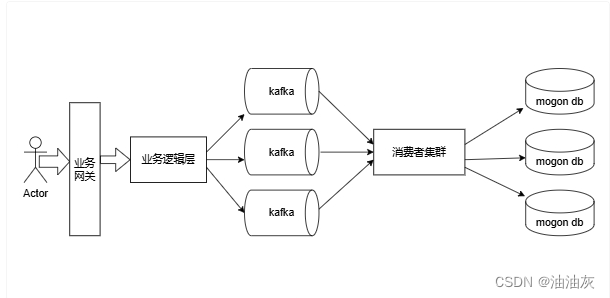
如何设计一个点赞系统
首先我们定义出一个点赞系统需要对外提供哪些接口: 1.用户对特定的消息进行点赞; 2.用户查看自己发布的某条消息点赞数量以及被哪些人赞过; 3.用户查看自己给哪些消息点赞过; 这里假设每条消息都有一个message_id, 每一个用户都…...

对象存储测试工具-s3cmd
一、环境安装 官网:https://s3tools.org/s3cmd 下载安装包:https://s3tools.org/download GitHub:https://github.com/s3tools/s3cmd/releases 本文安装包:https://github.com/s3tools/s3cmd/releases/download/v2.0.2/s3cmd-2.0…...

OpenCV--图像色彩空间及转换
图像色彩空间及转换 python代码和笔记 python代码和笔记 import cv2 色彩空间,基础:RGB或BGR OpenCV中: 一、HSV(HSB):用的最多, Hue:色相-色彩(0-360),红色:0,绿色&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
