【深度学习】GELU激活函数是什么?
torch.nn.GELU 模块在 PyTorch 中实现了高斯误差线性单元(GELU)激活函数。GELU 被用于许多深度学习模型中,包括Transformer,因为它相比传统的 ReLU(整流线性单元)函数能够更好地近似神经元的真实激活行为。
概述
- 功能: 应用 GELU 激活函数。
- 公式: GELU 激活函数可以表示为:
GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) GELU(x)=x⋅Φ(x)
其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的累积分布函数。
使用方法
要在神经网络中使用 torch.nn.GELU 模块,你可以简单地导入它并将其添加到模型的层中。以下是一个示例:
import torch
import torch.nn as nnclass MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()self.layer1 = nn.Linear(10, 20)self.gelu = nn.GELU()self.layer2 = nn.Linear(20, 10)def forward(self, x):x = self.layer1(x)x = self.gelu(x)x = self.layer2(x)return x# 创建模型实例
model = MyModel()# 创建一个随机输入张量
input_tensor = torch.randn(5, 10)# 前向传播
output_tensor = model(input_tensor)
print(output_tensor)
解释
nn.Linear(10, 20): 一个线性层,输入大小为 10,输出大小为 20。nn.GELU(): GELU 激活函数,应用于第一个线性层的输出。nn.Linear(20, 10): 另一个线性层,输入大小为 20,输出大小为 10。
GELU 激活函数用于在模型中引入非线性,这有助于模型学习更复杂的模式。
GELU 的优点
- 平滑近似: GELU 提供了一种比 ReLU 更平滑的神经元激活近似,这可以帮助训练的稳定性和收敛性。
- 概率解释: 通过结合累积分布函数,GELU 以更有原则的方式考虑激活的概率,这可能在某些模型(尤其是自然语言处理 (NLP) 和计算机视觉 (CV) 中)带来更好的性能。
通过在你的 PyTorch 模型中使用 torch.nn.GELU,你可以利用这些优点来提高神经网络的性能和训练动态。
GELU(Gaussian Error Linear Unit)激活函数是在论文《Gaussian Error Linear Units (GELUs)》中提出的。这篇论文由 Dan Hendrycks 和 Kevin Gimpel 于 2016 年发表。
以下是使用 Python 和 Matplotlib 绘制 GELU 激活函数的函数曲线的代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf# 定义 GELU 激活函数
def gelu(x):return 0.5 * x * (1 + erf(x / np.sqrt(2)))# 生成 x 轴数据
x = np.linspace(-3, 3, 400)
# 计算 y 轴数据
y = gelu(x)# 绘制 GELU 激活函数曲线
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='GELU', color='blue')
plt.title('GELU Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.show()
运行上述代码将生成一个展示 GELU 激活函数的曲线图:
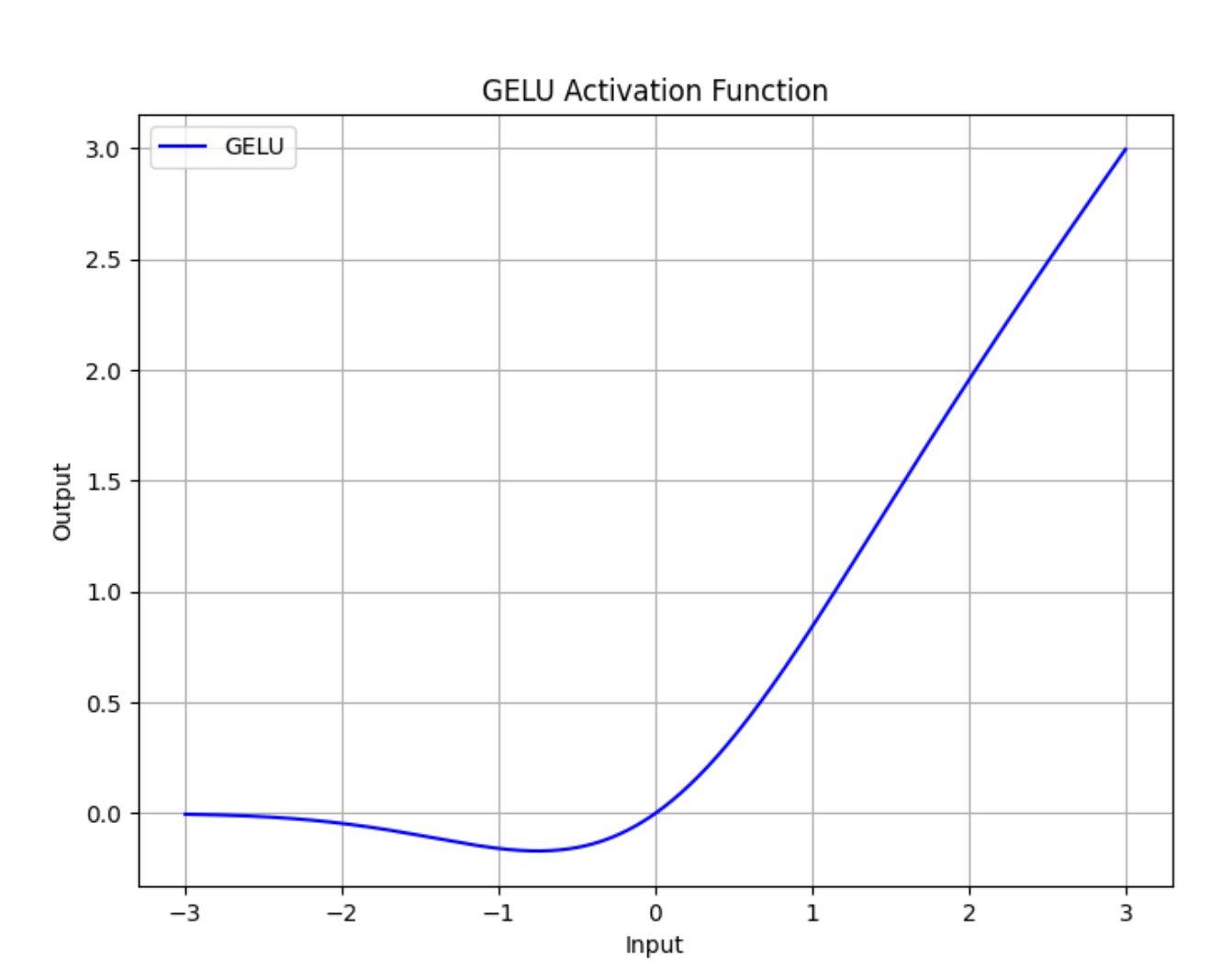
优点:
- 平滑的近似:
GELU 提供了比 ReLU 更平滑的激活函数,这有助于神经网络更稳定地训练并提高收敛性。ReLU 在负数区间完全关闭,而 GELU 会根据输入值的大小逐渐激活神经元。
- 概率解释:
GELU 将标准正态分布的累积分布函数(CDF)结合到激活函数中,以一种更有原则的方式处理激活的概率。这种方法考虑了输入值的分布,使得神经网络可以更有效地处理不同范围的输入。
- 更好的性能:
由于 GELU 函数的平滑性和概率解释,它在处理某些任务时(尤其是在自然语言处理 (NLP) 和计算机视觉 (CV) 任务中)表现出色。在这些任务中,GELU 激活函数可以提高模型的性能。
- 渐进式变化:
相对于 ReLU 的硬边界(即大于零输出本身,小于零输出零),GELU 提供了一种更加渐进式的激活方式,使得小负值输入仍然能够产生一定的激活效果,这在某些情况下可以提高模型的表现。
GELU 反向传播的公式
GELU 激活函数的公式
GELU 激活函数定义为:
GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) GELU(x)=x⋅Φ(x)
其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的累积分布函数。 Φ ( x ) \Phi(x) Φ(x) 的表达式为:
Φ ( x ) = 1 2 ( 1 + erf ( x 2 ) ) \Phi(x) = \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) Φ(x)=21(1+erf(2x))
GELU 的梯度公式
为了求 GELU 的梯度,我们需要对其进行求导。这里 erf ( x ) \text{erf}(x) erf(x) 是误差函数,定义为:
erf ( x ) = 2 π ∫ 0 x e − t 2 d t \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt erf(x)=π2∫0xe−t2dt
求导过程
GELU 的导数可以表示为:
d d x GELU ( x ) = d d x ( x ⋅ Φ ( x ) ) \frac{d}{dx} \text{GELU}(x) = \frac{d}{dx} \left( x \cdot \Phi(x) \right) dxdGELU(x)=dxd(x⋅Φ(x))
根据乘积法则:
d d x ( x ⋅ Φ ( x ) ) = Φ ( x ) + x ⋅ d d x Φ ( x ) \frac{d}{dx} \left( x \cdot \Phi(x) \right) = \Phi(x) + x \cdot \frac{d}{dx} \Phi(x) dxd(x⋅Φ(x))=Φ(x)+x⋅dxdΦ(x)
我们需要对 Φ ( x ) \Phi(x) Φ(x) 进行求导:
d d x Φ ( x ) = d d x ( 1 2 ( 1 + erf ( x 2 ) ) ) \frac{d}{dx} \Phi(x) = \frac{d}{dx} \left( \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) \right) dxdΦ(x)=dxd(21(1+erf(2x)))
由于常数部分导数为零,我们仅对 erf ( x 2 ) \text{erf}\left( \frac{x}{\sqrt{2}} \right) erf(2x) 进行求导:
d d x erf ( x 2 ) = 2 π e − ( x 2 ) 2 ⋅ 1 2 = e − x 2 / 2 2 π \frac{d}{dx} \text{erf}\left( \frac{x}{\sqrt{2}} \right) = \frac{2}{\sqrt{\pi}} e^{-\left( \frac{x}{\sqrt{2}} \right)^2} \cdot \frac{1}{\sqrt{2}} = \frac{e^{-x^2/2}}{\sqrt{2\pi}} dxderf(2x)=π2e−(2x)2⋅21=2πe−x2/2
所以:
d d x Φ ( x ) = 1 2 π e − x 2 / 2 \frac{d}{dx} \Phi(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdΦ(x)=2π1e−x2/2
将其代入前面的公式,我们得到:
d d x GELU ( x ) = Φ ( x ) + x ⋅ 1 2 π e − x 2 / 2 \frac{d}{dx} \text{GELU}(x) = \Phi(x) + x \cdot \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdGELU(x)=Φ(x)+x⋅2π1e−x2/2
因此,GELU 的梯度为:
d d x GELU ( x ) = 1 2 ( 1 + erf ( x 2 ) ) + x ⋅ 1 2 π e − x 2 / 2 \frac{d}{dx} \text{GELU}(x) = \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) + x \cdot \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdGELU(x)=21(1+erf(2x))+x⋅2π1e−x2/2
Python 代码绘制 GELU 梯度曲线
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf, erfc# 定义 GELU 激活函数
def gelu(x):return 0.5 * x * (1 + erf(x / np.sqrt(2)))# 定义 GELU 激活函数的导数
def gelu_derivative(x):return 0.5 * (1 + erf(x / np.sqrt(2))) + (x * np.exp(-x**2 / 2)) / np.sqrt(2 * np.pi)# 生成 x 轴数据
x = np.linspace(-3, 3, 400)
# 计算 y 轴数据
y = gelu(x)
# 计算 y' 轴数据
dy = gelu_derivative(x)# 绘制 GELU 激活函数和梯度曲线
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='GELU', color='blue')
plt.plot(x, dy, label='GELU Derivative', color='red', linestyle='dashed')
plt.title('GELU Activation Function and Its Derivative')
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.show()
运行这段代码将生成一个展示 GELU 激活函数及其梯度的曲线图,有助于直观地理解 GELU 在反向传播中的行为:
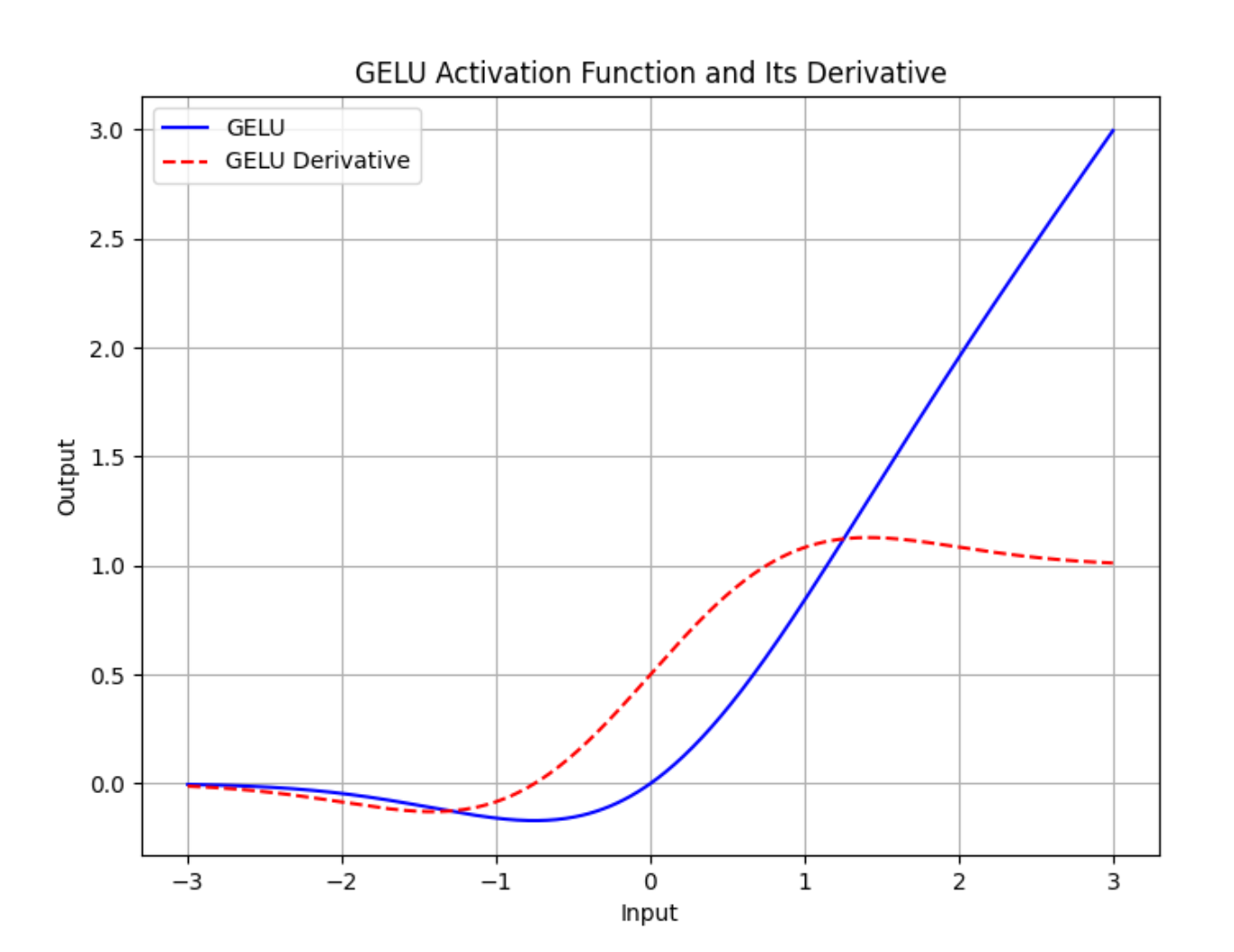
相关文章:

【深度学习】GELU激活函数是什么?
torch.nn.GELU 模块在 PyTorch 中实现了高斯误差线性单元(GELU)激活函数。GELU 被用于许多深度学习模型中,包括Transformer,因为它相比传统的 ReLU(整流线性单元)函数能够更好地近似神经元的真实激活行为。…...

如何编译和运行您的第一个Java程序
如何编译和运行您的第一个Java程序 让我们从一个简单的java程序开始。 简单的Java程序 这是一个非常基本的java程序,它会打印一条消息“这是我在java中的第一个程序”。 public class FirstJavaProgram {public static void main(String[] args){System.…...

vscode用vue框架写一个登陆页面
目录 一、创建登录页面 二、构建好登陆页面的路由 三、编写登录页代码 1.添加基础结构 2.给登录页添加背景 3.解决填充不满问题 4.我们把背景的红颜色替换成背景图: 5.在页面中央添加一个卡片来显示登录页面 6.设置中间卡片页面的左侧 7.设置右侧的样式及…...

腾讯云API安全保障措施?有哪些调用限制?
腾讯云API的调用效率如何优化?怎么使用API接口发信? 腾讯云API作为腾讯云提供的核心服务之一,广泛应用于各行各业。然而,随着API应用的普及,API安全问题也日益突出。AokSend将详细探讨腾讯云API的安全保障措施&#x…...

在建设工程合同争议案件中,如何来认定“竣工验收”?
在建设工程合同争议案件中,如何来认定“竣工验收”? 建设工程的最终竣工验收,既涉及在建设单位组织下的五方单位验收,又需政府质量管理部门的监督验收以及竣工验收备案,工程档案还需递交工程所在地的工程档案馆归档。…...
Linux:多线程中的互斥与同步
多线程 线程互斥互斥锁互斥锁实现的原理封装原生线程库封装互斥锁 死锁避免死锁的四种方法 线程同步条件变量 线程互斥 在多线程中,如果存在有一个全局变量,那么这个全局变量会被所有执行流所共享。但是,资源共享就会存在一种问题࿱…...

数据仓库之主题域
数据仓库的主题域(Subject Area)是按照特定业务领域或主题对数据进行分类和组织的方式。每个主题域集中反映一个特定的业务方面,使得数据分析和查询更加清晰和高效。主题域通常与企业的关键业务过程相关,能够帮助用户在数据仓库中…...

【简易版tinySTL】 vector容器
文章目录 基本概念功能思路代码实现vector.htest.cpp 代码详解变量构造函数析构函数拷贝构造operatorpush_backoperator[]insertprintElements 本实现版本 和 C STL标准库实现版本的区别: 基本概念 vector数据结构和数组非常相似,也称为单端数组vector与…...
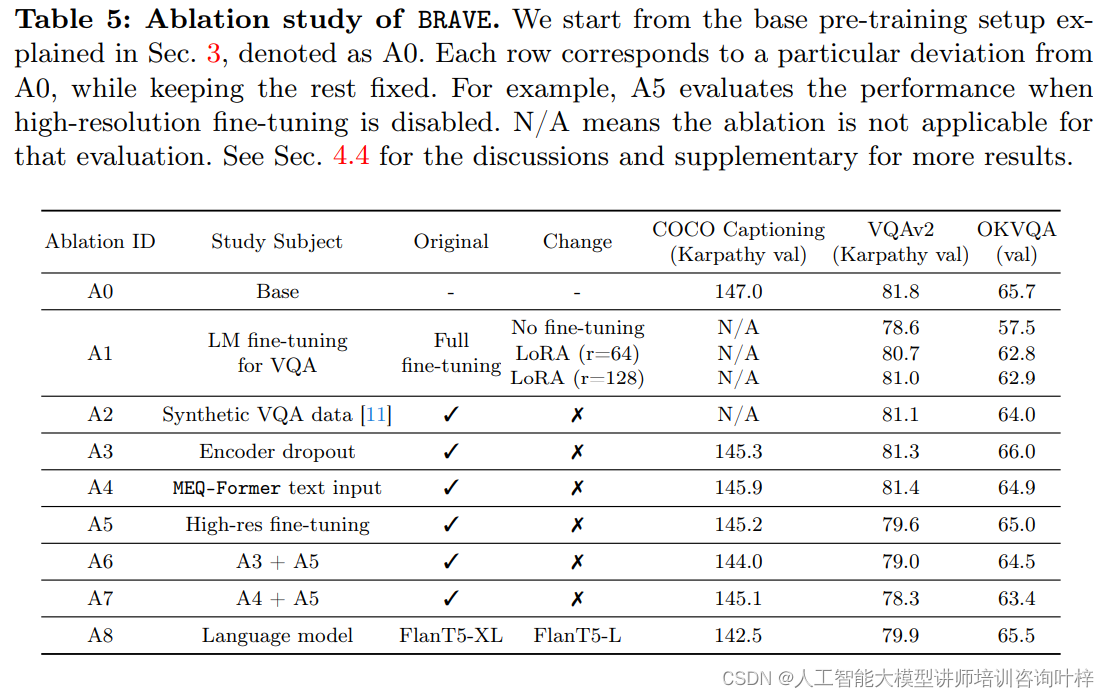
BRAVE:扩展视觉编码能力,推动视觉-语言模型发展
视觉-语言模型(VLMs)在理解和生成涉及视觉与文本的任务上取得了显著进展,它们在理解和生成结合视觉与文本信息的任务中扮演着重要角色。然而,这些模型的性能往往受限于其视觉编码器的能力。例如,现有的一些模型可能对某…...

使用 Verdaccio 建立私有npm库
网上有很多方法,但很多没标注nginx的版本所以踩了一些坑,下方这个文档是完善后的,对linux不是很熟练,所以不懂linux不会搭建的跟着做就可以了 搭建方法 首先需要一台云服务器 以139.196.226.123为例登录云服务器 下载node cd /usr/local/lib下载node 解压 下载 wget https://…...
)
个人职业规划(含前端职业+技术线路)
1. 了解自己的兴趣与长处 喜欢擅长的事 职业方向 2. 设定长期目标(5年) 目标内容 建立自己的品牌建立自己的社交网络 适量参加社交活动,认识更多志同道合的小伙伴寻求导师指导 建立自己的作品集 注意事项 每年元旦进行审视和调整永葆积极…...
LeetCode | 344.反转字符串
设置头尾两个指针,依靠中间变量temp交换头尾指针所指元素,头指针后移,尾指针前移,直到头尾指针重合或者头指针在尾指针后面一个元素 class Solution(object):def reverseString(self, s):""":type s: List[str]:r…...

一步一步用numpy实现神经网络各种层
1. 首先准备一下数据 if __name__ "__main__":data np.array([[2, 1, 0],[2, 2, 0],[5, 4, 1],[4, 5, 1],[2, 3, 0],[3, 2, 0],[6, 5, 1],[4, 1, 0],[6, 3, 1],[7, 4, 1]])x data[:, :-1]y data[:, -1]for epoch in range(1000):...2. 实现SoftmaxCrossEntropy层…...
)
vue学习(二)
9.vue中的数据代理 通过vm对象来代理data对象中的属性操作(读写),目的是为了更加方便操作data中的数据 基本原理:通过Object.defineProperty()把data对象所有属性添加到vm上,为每一个添加到vm上的属性,都增…...
Maven 介绍
Maven open in new window 官方文档是这样介绍的 Maven 的: Apache Maven is a software project management and comprehension tool. Based on the concept of a project object model (POM), Maven can manage a projects build, reporting and documentation fr…...

QT截图程序三-截取自定义多边形
上一篇文章QT截图程序,可多屏幕截图二,增加调整截图区域功能-CSDN博客描述了如何截取,具备调整边缘功能后已经方便使用了,但是与系统自带的程序相比,似乎没有什么特别,只能截取矩形区域。 如果可以按照自己…...

Unity的三种Update方法
1、FixedUpdate 物理作用——处理物理引擎相关的计算和刚体的移动 (1) 调用时机:在固定的时间间隔内,而不是每一帧被调用 (2) 作用:用于处理物理引擎的计算,例如刚体的移动和碰撞检测 (3) 特点:能更准确地处理物理…...
[Python学习篇] Python字典
字典是一种可变的、无序的键值对(key-value)集合。字典在许多编程(Java中的HashMap)任务中非常有用,因为它们允许快速查找、添加和删除元素。字典使用花括号 {} 表示。字典是可变类型。 语法: 变量 {key1…...

react项目中如何书写css
一:问题: 在 vue 项目中,我们书写css的方式很简单,就是在 .vue文件中写style标签,然后加上scope属性,就可以隔离当前组件的样式,但是在react中,是没有这个东西的,如果直…...

PostgreSQL源码分析——绑定变量
这里分析一下函数中应用绑定变量的问题,但实际应用场景中,不推荐这么使用。 prepare divplan2(int,int) as select div($1,$2); execute divplan2(4,2);语法解析 分别分析prepare语句以及execute语句。 gram.y中定义 /******************************…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
