MySQL:SELECT list is not in GROUP BY clause 报错 解决方案
一、前言
一大早上测试环境,发现测试环境的MySQL报错了。
SELECT list is not in GROUP BY clause and contains nonaggregated column二、解决方案
官方文档中提到:

大致意思:
用于GROUP BY的SQL / 92标准要求满足以下条件:
- SELECT子句的表达式中使用的列必须在GROUP BY子句中。否则,使用该列的表达式是一个聚合函数。
- GROUP BY表达式只能包含选择列表中的列名,而不能仅用作向量聚合的参数。
- 首先执行以下查询:
不出所料就是有一个ONLY_FULL_GROUP_BY
SELECT @@sql_mode;ONLY_FULL_GROUP_BY,STRICT_TRANS_TABLES,NO_ZERO_IN_DATE,NO_ZERO_DATE,ERROR_FOR_DIVISION_BY_ZERO,NO_ENGINE_SUBSTITUTION
所以我去到配置文件中,在 mysqld 下配置一下 sql_mode,把 ONLY_FULL_GROUP_BY 去掉
# 添加的行如下
sql_model=STRICT_TRANS_TABLES,NO_ZERO_IN_DATE,NO_ZERO_DATE,ERROR_FOR_DIVISION_BY_ZERO,NO_ENGINE_SUBSTITUTION
重启MySQL即可!
可以参考我之前写的一篇文章了解sql_mode中的每个项的意思:点此跳转链接
三、起因分析
起因是昨天修改一个数据表的结构保存失败出现了报错:
1812 - Tablespace is missing for table database/crm_bid_deposit.
这个错误导致我删除表也删不掉,备份数据库也不行,烦死了。
然后翻遍谷歌,
我做了以下尝试:
- 删除MySQL data目录下对应表的
.ibd文件,重启MySQL,再去Navicat那边删除对应的表,失败! - 修改配置项
innodb_file_per_table=0,重启,执行过以下命令,失败:
SET FOREIGN_KEY_CHECKS=0;
ALTER TABLE wk_crm_table.wk_crm_bid_deposit DISCARD TABLESPACE;
ALTER TABLE wk_crm_table.wk_crm_bid_deposit IMPORT TABLESPACE;REPAIR TABLE wk_crm_bid_deposit;
无论我怎么操作,Navicat那边还是看到那个数据表
无奈只能先把innodb_file_per_table=1设置回来了,重启之后没检查,只看了Navicat中操作的表都没问题,没注意看web应用程序查询是否正常。所以早上来了才发现标题中提到的这个错误。
我这个 Tablespace is missing for table database/crm_bid_deposit. 错误看来只能是等周末再一个个表导出来重建数据库了。有没有人有解决方案,救救我~
相关文章:

MySQL:SELECT list is not in GROUP BY clause 报错 解决方案
一、前言 一大早上测试环境,发现测试环境的MySQL报错了。 SELECT list is not in GROUP BY clause and contains nonaggregated column二、解决方案 官方文档中提到: 大致意思: 用于GROUP BY的SQL / 92标准要求满足以下条件: SE…...

IPython的使用技巧
1、解释说明 IPython是一个强大的Python交互式shell,它提供了丰富的功能,如自动补全、历史记录、内置帮助等。IPython使得在命令行下编写和测试Python代码变得更加方便和高效。 2、使用示例 安装IPython: pip install ipython启动IPython…...

Spring Boot 多线程例子
在Spring Boot中,多线程可以通过Java的并发工具来实现。以下是一些常见的多线程实现方法: 1. 使用Async注解和CompletableFuture: 首先,需要在Spring Boot应用的主类上添加EnableAsync注解,以启用异步支持。 java Spr…...

java干货 线程池的分析和使用
文章目录 一、了解线程池1.1 什么是线程池1.2 为什么需要线程池 二、四种线程池的使用2.1 newFixedThreadPool2.2 newCachedThreadPool2.3 newSingleThreadExecutor2.4 newScheduledThreadPool 三、自定义线程池3.1 线程池七大核心参数3.2 线程池内部处理逻辑 一、了解线程池 …...

文本张量入门
张量,英文为Tensor,是机器学习的基本构建模块,是以数字方式表示数据的形式。 张量的基本类型: 创建一个标量(0维张量),也就是一个单独的数字 scalar torch.tensor(7) scalar.ndim # 返回张量的维度 0 # …...

js文字如何轮播?
<div class"td-style"> <span class"td-text">内容1内容1内容1内容1内容1内容1</span> </div> css: <style> .td-style { width: 160px; height: 72px; overflow: hidden; white-…...

Linux 五种IO模型
注:还有一种信号驱动IO,使用较少暂不讨论; 一,区分阻塞、非阻塞和同步、异步 看了很多文章对这两组概念解释和对比,说的太复杂了,其实没必要,两句话就能说清楚。 首先,对于读数据rec…...
深度解析响应式异步编程模型
上一篇文章中我们聊了一下线程池,基于线程池的多线程编程是我们在高并发场景下提升系统处理效率的有效手段,但却不是唯一的。今天我们来看一下另一种异步开发的常用手段-响应式编程模型 传统多线程模型的缺陷 多线程模型是目前应用最为广泛的并发编程手段,但凡遇到什么性能…...

一个软件是如何开发出来的呢?
一、前言 如今,AI大爆发的时代,作为一名IT从业者,你是否也想尝试开发一套自己的系统,实现那些看似有可能实现的天马行空的想法,变成一个优秀甚至伟大的产品,甚至带来某个行业的革新,那作为一名…...

宝塔板面有哪些优势
哈喽呀,大家好呀,淼淼又来和大家见面啦,在当今数字化时代,随着云计算和互联网技术的飞速发展,服务器管理成为了许多企业和个人开发者不可或缺的一部分。然而,传统服务器管理方式的复杂性和技术门槛往往令初…...
Mybatis中BaseEntity作用
新建各种对象的时候,一般来说,有几个属性是所有对象共有的,比如说id,is_del,is_enable这些,然后设置一个基础对象,以后新建所有对象的时候都继承它,就省的每次都要写这些共有的属性了...
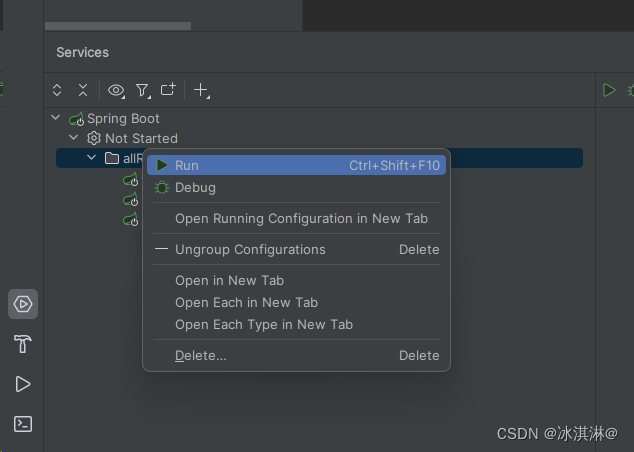
IDEA2023中使用run Dashboard面板?实现批量运行微服务
1、直接点击Add service--->Run Configuration Type---->Spring Boot 2、这样就出现了run Dashboard面板,可同时运行多个工程模块,shift选中所有启动类组命名(Group Configurations) 3、启动所有的项目...

分数受限,鱼和熊掌如何兼得?专业or学校,这样选最明智!
文章目录 引言一、专业解析二、名校效应分析三、好专业和好学校的权衡结论个人建议 引言 24年高考帷幕落下,一场新的思考与选择悄然来临。对于每一位高考考生,学校和专业都是开启大学新生活的两个前置必选项。但有时候“鱼与熊掌不可兼得”,…...

CentOS 8.5 - 配置ssh的免密登录
文章目录 生成ssh密钥公钥内容放入服务器 生成ssh密钥 在本地主机安装 ssh工具,并生成公钥、私钥。 # 命令行输入 ssh-keygen -r rsa# 会在当前用户的家目录下生成一个.ssh目录公钥内容放入服务器 将上一步生成的id_rsa.pub公钥的内容复制到远程服务器 # 编辑文…...
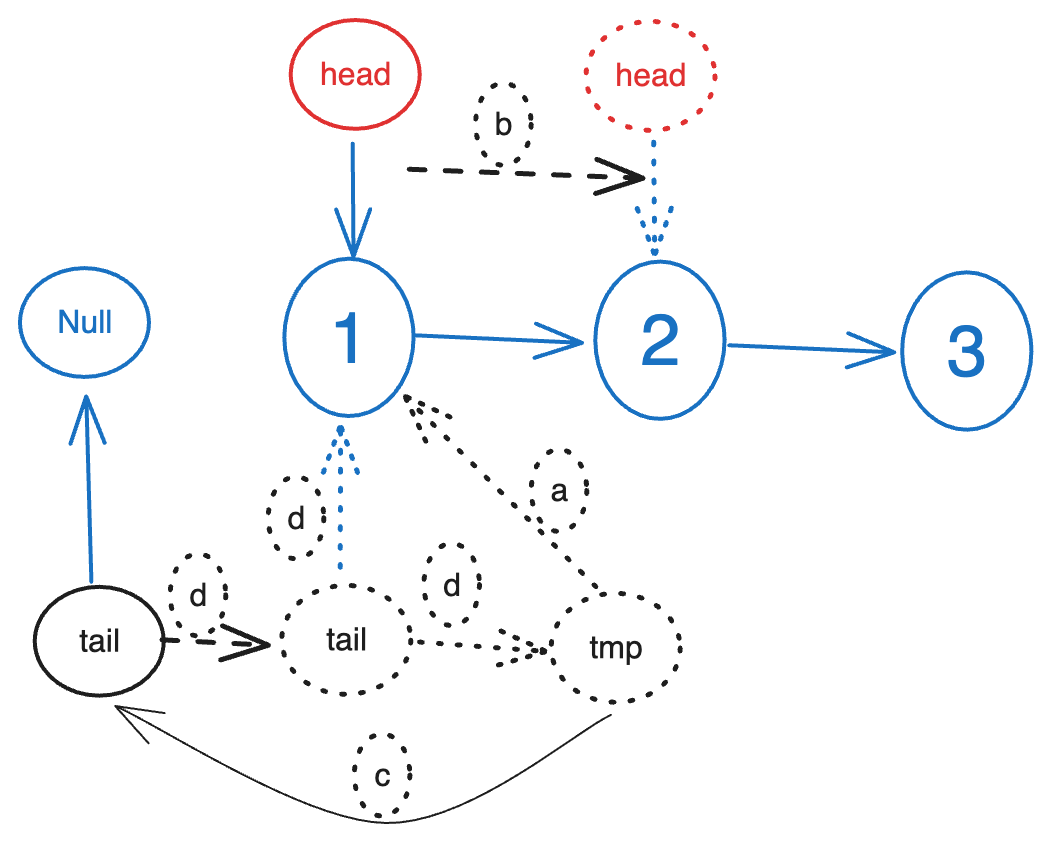
反转链表(java精简版)
反转一个单向链表。 public class ReversingLinkedList {static class Node {int val;Node next;public Node(int val) {this.val val;}public boolean hasNext() {return next ! null;}}public static void main(String[] args) {//构造Node head null;Node shift null;for…...

QPair使用详解
QPair使用详解 一、创建和初始化 QPair1.1 QPair默认构造1.2 使用值初始化1.3 QPair拷贝构造 二、访问 QPair 的值2.1 修改 QPair 的值2.2 比较 QPair2.3 使用 qMakePair 辅助函数2.4 使用 QPair 的场景 三、QPair自定结构体3.1 定义自定义结构体3.2 在 QPair 中使用自定义结构…...
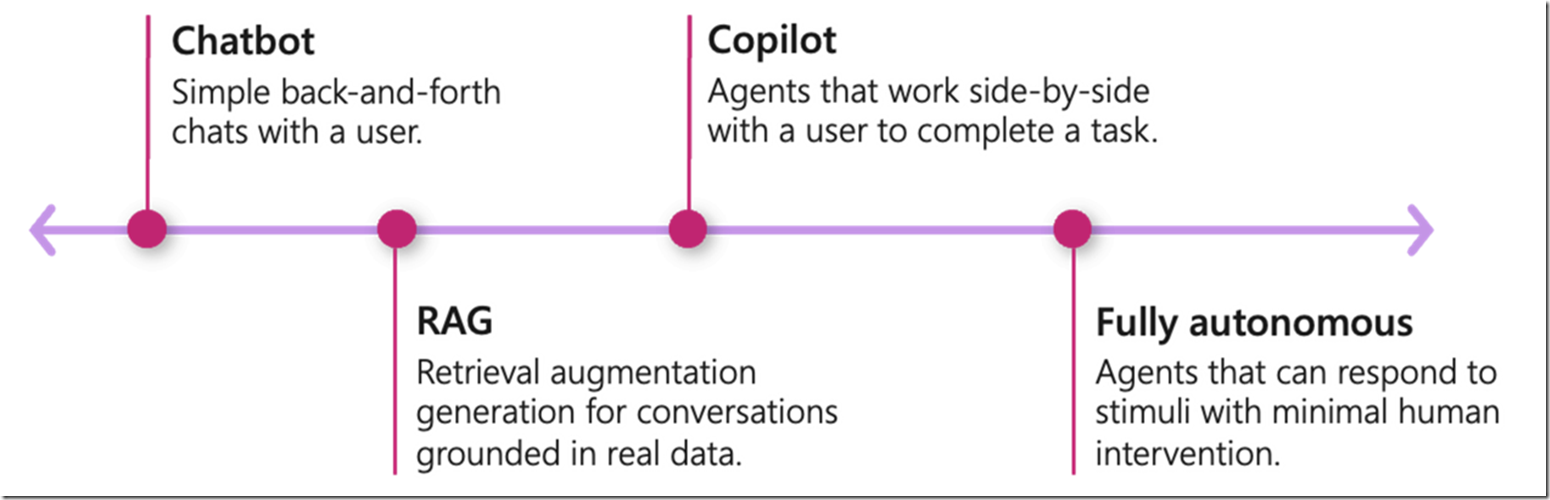
C# 语言在AGI 赛道上能做什么
自从2022年11月OpenAI正式对外发布ChatGPT依赖,AGI 这条赛道上就挤满了重量级的选手,各大头部公司纷纷下场布局。原本就在机器学习、深度学习领域占据No.1的Python语言更是继续稳固了自己AI一哥的位置。凭借着Microsoft 和 OpenAI 长期以来一直是紧密相连…...

微信小程序-API 本地存储
一.本地存储-同步API 存储 : wx.setStorageSync 获取:wx.getStorageSync 删除:wx.removeStorageSync 清空:wx.clearStorageSync 代码: save(){//存储wx.setStorageSync(id, 1) wx.setStorageSync(obj, {name:"te…...

TensorFlow音频分类修复
原先传wav格式,后来发现前端生成的wav格式不完整 后端改mp3 其实是mp3和wav都可以接收 前端MP3和wav格式不正确,导致可以接收,但都无法计算时长 该文作废,可能导致音频分类不准确 修复TensorFlow放到生产后报错问题-CSDN博客 依赖 <dependency><groupId>or…...

C#学习系列之ListView垂直滚动
C#学习系列之ListView垂直滚动 前言垂直滚动总结 前言 当ListView中不断增加新内容,经常是纵向滚动。 垂直滚动 这个是关键:<VirtualizingStackPanel/> <ListView.ItemsPanel><ItemsPanelTemplate><VirtualizingStackPanel/>&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
