【Java算法】滑动窗口

  🔥个人主页： 中草药

🔥专栏：【算法工作坊】算法实战揭秘

---

👖一. 长度最小的子数组

题目链接：209.长度最小的子数组

算法原理

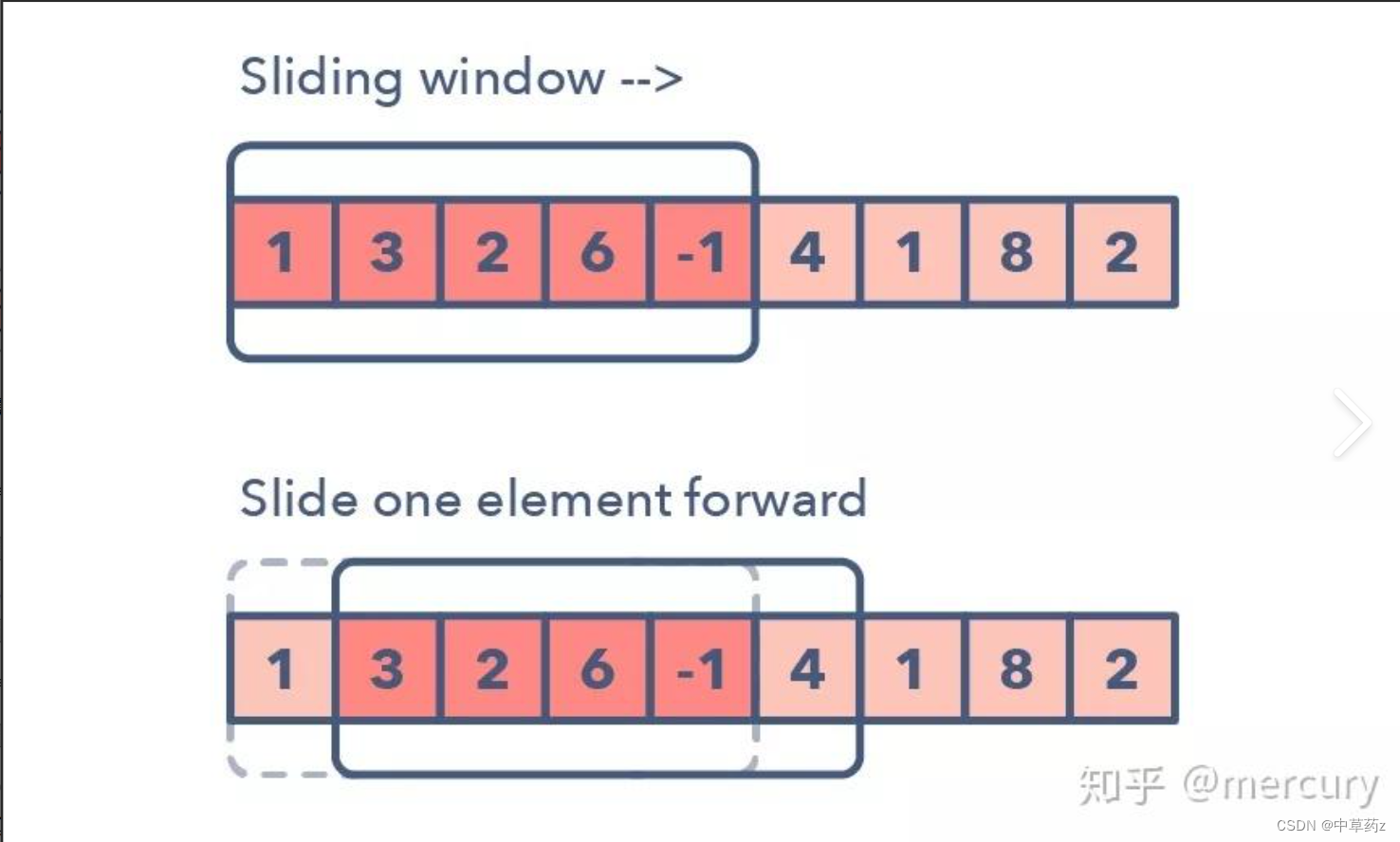
滑动窗口

滑动窗口算法常用于处理数组/字符串等序列问题，通过定义一个窗口（即一段连续的元素），并根据某种条件动态调整窗口的左右边界来找到满足条件的子序列。

在这个问题中，滑动窗口的具体应用如下：

1. 初始化：设置两个指针 left 和 right，均初始化为0，表示窗口的左右边界。同时，初始化 sum 为0，用于累计窗口内元素的和，minlen 设置为 Integer.MAX_VALUE，用于记录符合条件的最小子数组长度。

2. 扩展右边界：不断将右指针 right 向右移动，并将 nums[right] 加入到 sum 中，这相当于不断扩大窗口右侧，尝试包含更多的元素以满足和至少为 target 的条件。

3. 收缩左边界：当窗口内的元素和 sum 至少达到 target 时，开始尝试缩小窗口左侧，即增加 left 指针的值，并从 sum 中减去移出窗口的元素 nums[left]。这个过程会持续进行，直到 sum 小于 target，确保每次收缩都检查当前窗口是否仍然满足条件。

4. 更新最小长度：在每次收缩窗口后（即 sum 小于等于 target 时），用当前窗口的长度（right - left + 1）更新 minlen，保持记录最短的满足条件的子数组长度。

5. 遍历结束：当右指针遍历完整个数组后，检查 minlen 是否仍为初始值 Integer.MAX_VALUE，如果是，则说明没有找到满足条件的子数组，返回0；否则返回 minlen 作为结果。

时间复杂度与空间复杂度

• 时间复杂度：O(n)，其中n为数组 nums 的长度。每个元素最多被访问两次，一次作为窗口扩展时加入，一次作为窗口收缩时移除。
• 空间复杂度：O(1)，只使用了固定数量的变量，与输入数组大小无关。

综上所述，这段代码利用滑动窗口算法高效地解决了寻找最小长度子数组使其和至少为目标值的问题。

代码

public int minSubArrayLen(int target, int[] nums) {int sum=0,minlen=Integer.MAX_VALUE;//无穷大for(int left=0,right=0;right<nums.length;right++){sum+=nums[right];//进窗口while(sum>=target){//出窗口minlen=Math.min(minlen,right-left+1);sum-=nums[left++];}}if(minlen==Integer.MAX_VALUE){return 0;}return minlen;}

举例

测试用例 [2,3,1,2,4,3]

初始状态

• sum = 0
• minlen = Integer.MAX_VALUE
• 初始化双指针：left = 0, right = 0

执行过程

第一轮迭代

• right=0: sum += nums[0] = 2, 现在 sum = 2, 不满足 sum >= target，right++。
• right=1: sum += nums[1] = 3, 现在 sum = 5, 不满足 sum >= target，right++。
• right=2: sum += nums[2] = 1, 现在 sum = 6, 不满足 sum >= target，right++。
• right=3: sum += nums[3] = 2, 现在 sum = 8, 满足 sum >= target。

这时进入内部的 while 循环。

第一次窗口收缩

• sum >= target，计算子数组长度 right-left+1 = 4，更新 minlen = Math.min(minlen, 4) = 4。
• 从 sum 中减去 nums[left++] = nums[0] = 2，得到 sum = 6，继续在循环内检查。
• 再次检查 sum >= target，是的，所以继续收缩。
• 从 sum 中减去 nums[left++] = nums[1] = 3，得到 sum = 3，现在 sum < target，退出 while 循环。

接下来

• 继续移动 right，累加 sum 直至再次满足条件或遍历完数组。

第二次满足条件

• right=4: sum += nums[4] = 4，现在 sum = 7，满足 sum >= target。
• 计算子数组长度 right-left+1 = 2，更新 minlen = Math.min(minlen, 2) = 2。
• 由于这次 sum 正好等于 target，收缩窗口会导致 sum < target，因此不会进一步收缩。

遍历完成

• 继续移动 right，但不再有新的子数组满足条件且长度更小。

结果

遍历结束后，minlen = 2，这是满足条件的最小子数组长度，对应子数组是 [4,3]。

🩰二.无重复字符的最长子串

题目链接：3.无重复字符的最长子串

算法原理

1. 初始化：定义两个指针 left 和 right，初始都指向字符串的起始位置，即 left = 0，right = 0。hash 数组用于记录 ASCII 字符出现的次数（考虑到 ASCII 总共有 128 个字符，故数组大小为 128）。ret 用于存储最长无重复子串的长度，初始化为 0。

2. 扩展右边界：不断地将右指针 right 向右移动，每移动一次，就将当前字符 ch[right] 在 hash 数组中的计数加一。这意味着窗口正在尝试包含更多的字符。

3. 处理重复字符与收缩左边界：如果 hash[ch[right]] 大于 1，表明当前字符 ch[right] 已经在窗口内出现过，这时需要移动左指针 left，将 left 指向的字符在 hash 中的计数减一，同时左指针右移一位，以此来排除重复字符，保证窗口内的字符都是唯一的。

4. 更新最大长度：每次移动右指针时，都计算当前窗口的长度（即 right - left + 1），并将这个长度与当前已知的最大长度 ret 进行比较，取较大者更新 ret。这样可以保证 ret 始终保存着遇到过的最长无重复字符子串的长度。

5. 遍历结束：当右指针 right 遍历到字符串末尾时，循环结束，返回 ret 作为最终结果。

时间复杂度与空间复杂度

• 时间复杂度：O(n)，其中 n 是字符串的长度。每个字符最多被访问两次，一次作为右边界扩展，一次作为左边界收缩。
• 空间复杂度：O(1)，虽然使用了 hash 数组，但它是一个固定大小的数组（128），与输入字符串的长度无关，因此空间复杂度是常数级别的。

总之，这段代码通过巧妙地利用滑动窗口和哈希表（在这里是简化版的数组实现）减少了不必要的字符比较，从而高效地求解了最长无重复字符子串的长度问题。

代码

 public int lengthOfLongestSubstring(String s) {int left=0,right=0;char[] ch=s.toCharArray();int[] hash=new int[128];//用数组模拟哈希表int ret=0;while(right<s.length()){hash[ch[right]]++;while(hash[ch[right]]>1){hash[ch[left++]]--;}ret =Math.max(ret,right-left+1);right++;}return ret;}

 举例

测试用例 "abcabcbb"

初始化

• left = 0, right = 0
• char[] ch = {'a', 'b', 'c', 'a', 'b', 'c', 'b', 'b'}
• int[] hash 初始化为全0，用于记录字符出现次数
• ret = 0，用于记录最长无重复子串长度

执行过程

1. 右指针移动 & 记录字符

   • right=0: 'a'，hash['a'] = 1，right++
   • right=1: 'b'，hash['b'] = 1，right++
   • right=2: 'c'，hash['c'] = 1，right++。此时，窗口abc无重复字符，ret = 3

2. 发现重复，收缩左边界

   • right=3: 'a'，hash['a'] = 2，发现重复，开始收缩左边界，hash['a']--，left++

3. 继续扩展与收缩

   • right=4: 'b'，hash['b'] = 2，收缩左边界，hash['b']--，left++
   • right=5: 'c'，hash['c'] = 2，收缩左边界，hash['c']--，left++。此时窗口内为bc，无重复字符，ret保持为3

4. 重复与扩张

   • right=6: 'b'，hash['b'] = 3，收缩左边界，hash['b']--，left++
   • right=7: 'b'，hash['b'] = 3，继续收缩左边界，hash['b']--，left++。此时窗口为空，ret保持为3

结果

• 最后，所有字符遍历完毕，返回 ret 的值，即最长无重复字符的子串长度为 3。在这段字符串中，满足条件的最长子串是 "abc"。

这段代码通过动态调整窗口（由 left 和 right 定义）大小，有效利用哈希表（此处为简化版的 hash 数组）快速判断字符是否重复，最终找到了最长的无重复字符子串。

🎩三.最大连续1的个数III

题目链接：1004.最大连续1的个数III

算法原理

1. 初始化：定义三个指针 left, right, 和一个计数器 zero，分别用来表示窗口的左边界、右边界以及窗口内 0 的数量。同时，定义 ret 来存储最长子数组的长度，初始化为 0。

2. 扩展右边界：不断将右指针 right 向右移动，每次移动时检查新进入窗口的元素（nums[right]）是否为 0，如果是，则将 zero 计数器加 1。这意味着窗口正在尝试包含更多的元素，包括 0。

3. 处理限制条件：当窗口内 0 的数量超过了允许的最大数量 k 时，需要移动左指针 left 来缩小窗口，直到窗口内 0 的数量回到 k 或更少。在移动 left 的过程中，如果移出窗口的元素是 0，则将 zero 减 1。

4. 更新最长子数组长度：在每次移动右指针之后（即每次尝试扩大窗口或维持窗口大小但可能更新了窗口内容后），都会用当前的右指针减去左指针再加 1 来计算当前窗口的长度，并用这个长度去更新 ret 的值，保持 ret 存储的是最长子数组的长度。

5. 遍历结束：当右指针遍历完整个数组后，循环结束，此时 ret 中存储的就是满足条件的最长连续子数组的长度。

时间复杂度与空间复杂度

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。每个元素最多被遍历一次。
• 空间复杂度：O(1)，因为使用的变量数量是固定的，不依赖于输入数组的大小。

代码

public int longestOnes(int[] nums, int k) {int ret=0;for(int left=0,right=0,zero=0;right<nums.length;right++){if (nums[right]==0) zero++;while (zero>k){if (nums[left++]==0) zero--;}ret=Math.max(ret,right-left+1);}return ret;}

 举例

测试用例 [1,1,1,0,0,0,1,1,1,1,0]

初始化

• left = 0, right = 0, zero = 0, ret = 0。

执行过程

1. 右指针移动：初始化时数组内的前三个元素都是1，右指针向右移动，窗口内没有0，zero 仍为0，此时最长子数组长度为3，但随着右指针的移动，情况会变化。

2. 遇到0并处理：

   • 当 right = 3，遇到第一个0，zero = 1。
   • 当 right = 4，遇到第二个0，zero = 2，达到了 k = 2 的限制。
   • 此时窗口 [1,1,1,0,0]，满足条件，长度为5，更新 ret = 5。

3. 收缩左边界：

   • 当 right = 5，遇到第三个0，由于 zero 已经是2，需要移动左指针。当 left = 3，nums[left++] 是0，zero--，此时窗口内0的个数回到1，窗口变为 [1,0,0,1,0,0]。

4. 继续扩展右边界：

   • 继续移动右指针，忽略更多的0，直到 right = 8，窗口为 [0,0,1,1,1,1,1,1]，此时 zero = 2（最初的两个0），窗口长度为6，更新 ret = 6。

5. 之后的步骤：

   • 当 right 继续移动并遇到更多0时，由于已经找到了长度为6且满足条件的子数组，即使右边界继续扩大，也不会影响最终答案，因为任何新加入的0都会导致左侧边界相应移动，保持最多2个0在窗口内。

结论

• 最终返回 ret = 6，表示最长的连续子数组是 [0,0,1,1,1,1] 

🧢四.将x减到0的最小操作数

题目链接：11658.将x减到0的最小操作数

算法原理

1. 计算总和：首先遍历数组 nums，计算其所有元素之和 sum。如果 sum 小于目标值 x，直接返回 -1，因为无论如何操作都无法使子数组之和等于 x。

2. 确定目标值：需要找到一个和为目标 x 的子数组，但实际操作中，我们是在找一个和为 target = sum - x 的子数组。这是因为我们需要从总和中减去 x 来达到操作的目的。

3. 双指针滑动窗口：

   • 初始化两个指针 left 和 right 都为 0，同时维护一个变量 cur 表示当前窗口内的元素和。
   • 右指针 right 向右移动，将 nums[right] 加入当前窗口的和 cur。
   • 如果 cur 大于目标值 target，则说明当前窗口和过大，需要减小窗口左侧的值，即减去 nums[left] 并将 left 指针右移一位，同时更新 cur。
   • 当 cur 等于 target 时，说明找到了一个符合条件的子数组。此时更新最大长度 ret 为当前子数组的长度（right-left+1）。
   • 继续移动右指针，重复上述过程，直到右指针遍历完整个数组。

4. 结果处理：

   • 如果在整个过程中没有找到符合条件的子数组（即 ret 仍为初始值 -1），返回 -1。
   • 若找到了符合条件的子数组，返回数组长度减去找到的最长子数组长度，即 nums.length - ret。这代表需要的操作次数，因为要使得剩下的部分和为 x，整个数组的剩余部分（非连续子数组）需要通过减少操作来匹配。

时间复杂度与空间复杂度：

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。每个元素最多被访问两次，一次在计算总和时，一次在滑动窗口中。
• 空间复杂度：O(1)，使用的额外空间与输入数组的大小无关，只使用了几个固定变量。

代码

 public int minOperations(int[] nums, int x) {int sum=0;int ret=-1;for (int a : nums){sum+=a;}if(sum<x){return -1;}int target=sum-x;for (int left=0,right=0,cur=0;right<nums.length;right++){cur+=nums[right];while(cur>target){cur-=nums[left++];}if (cur==target){ret=Math.max(ret,right-left+1);}}if(ret==-1){return -1;}return nums.length-ret;}

举例

测试用例 nums=[1,1,4,2,3]，x=5

初始化

• 首先，遍历数组 nums 计算所有元素之和 sum。

  • sum = 1 + 1 + 4 + 2 + 3 = 11

• 检查 sum 是否小于 x，若小于则直接返回 -1，这里不适用，因为 11 >= 5。

• 计算目标和 target 为 sum - x。

  • target = 11 - 5 = 6

滑动窗口

接下来，使用双指针（left 和 right）进行滑动窗口操作，同时维护窗口内元素和 cur。

1. 初始化：left = 0, right = 0, cur = 0。

2. 遍历数组：

   • 右指针移动：right 开始从 0 向右移动，每次移动将 nums[right] 加入 cur。
     • 当 right = 0, cur = 0 + 1 = 1（此时 cur < target）
     • 当 right = 1, cur = 1 + 1 = 2（此时 cur < target）
     • 当 right = 2, cur = 2 + 4 = 6，此时 cur == target，记录子数组长度，ret = Math.max(ret, right-left+1) = Math.max(-1, 3) = 3，并且开始收缩窗口。
     • 由于 cur 等于 target，无需移动 left。

3. 继续移动右指针：

   • 当 right = 3, cur = 6 + 2 = 8（此时 cur > target），需要收缩窗口。
     • 移动 left，cur -= nums[left++] = 8 - 1 = 7，left = 1，此时 cur > target 继续移动 left。
     • 再次移动 left，cur -= nums[left++] = 7 - 1 = 6，left = 2，此时 cur == target，不需要进一步移动 left。

4. 遍历结束：

   • 右指针继续移动，但在本次测试用例中，不会再次找到满足条件的子数组，因此 ret 保持为 3。

结果处理

• 最后，检查 ret 是否为 -1，如果不是，则返回 nums.length - ret，因为这是从整个数组长度中减去满足条件的子数组长度，即需要操作的次数。
  • return nums.length - ret = 5 - 3 = 2

结论

对于测试用例 nums=[1,1,4,2,3] 和 x=5，这段代码会返回 2，意味着需要至少操作两次，使得数组中某一段连续子数组之和等于 x=5。具体来说，可以通过减少前两个元素各一次（即 1-1=0 和 1-1=0），使得剩下的数组 [0,0,4,2,3] 中 4+2=6 符合要求。

---

🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀

以上，就是本期的全部内容啦，若有错误疏忽希望各位大佬及时指出💐

  制作不易，希望能对各位提供微小的帮助，可否留下你免费的赞呢🌸