【智能算法应用】基于混合粒子群-蚁群算法的多机器人多点送餐路径规划问题
目录
- 1.算法原理
- 2.数学模型
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】粒子群算法(PSO)原理及实现
配餐顺序: 采用混合粒子群算法 || 路径规划: 采用蚁群算法
2.数学模型
餐厅送餐多机器人多点配送路径规划,对模型进行以下假设:
- 单个机器人的配送量无法满足多个客人的需求量
- 多个机器人同时从取餐点出发,对所有所有客人进行配餐,配餐完结束后再次回到起始点
- 餐厅包含9张桌子和1个配餐点
🍀此模型为带容量限制的物流路径规划问题CVRP和机器人避障路径规划结合问题🍀
配餐顺序: 采用混合粒子群算法 || 路径规划: 采用蚁群算法

目标函数:
m i n Z = ∑ i = 0 n ∑ j = 0 , j ≠ i n ∑ k d i j x i j k (1) min Z=\sum_{i=0}^n\sum_{j=0,j\neq i}^n\sum_kd_{ij}x_{ijk}\tag{1} minZ=i=0∑nj=0,j=i∑nk∑dijxijk(1)
每个餐桌只能被访问一次:
∑ i = 0 n ∑ k x i j k = 1 ∀ j ∈ V , j ≠ 0 (2) \sum_{i=0}^n\sum_kx_{ijk}=1\quad\forall j\in V,j\neq0\tag{2} i=0∑nk∑xijk=1∀j∈V,j=0(2)
保证路径的连续性和回路的完整性:
∑ i = 0 , i ≠ j n x i j k = ∑ h = 0 , h ≠ j n x j h k ∀ j ∈ V , ∀ k (3) \sum_{i=0,i\neq j}^nx_{ijk}=\sum_{h=0,h\neq j}^nx_{jhk}\quad\forall j\in V,\forall k\tag{3} i=0,i=j∑nxijk=h=0,h=j∑nxjhk∀j∈V,∀k(3)
机器人容量限制:
∑ i = 0 n ∑ j = 0 , j ≠ i n q j x i j k ≤ Q ∀ k (4) \sum_{i=0}^n\sum_{j=0,j\neq i}^nq_jx_{ijk}\leq Q\quad\forall k\tag{4} i=0∑nj=0,j=i∑nqjxijk≤Q∀k(4)
每个餐桌的需求量被满足:
∑ i = 0 n ∑ k q j x i j k = q j ∀ j ∈ V (5) \sum_{i=0}^n\sum_kq_jx_{ijk}=q_j\quad\forall j\in V\tag{5} i=0∑nk∑qjxijk=qj∀j∈V(5)
路径的合法性(避免障碍物):
x i j k = 0 如果路径 ( i , j ) 不可行 (6) x_{ijk}=0\quad\text{如果路径 }(i,j)\text{ 不可行}\tag{6} xijk=0如果路径 (i,j) 不可行(6)
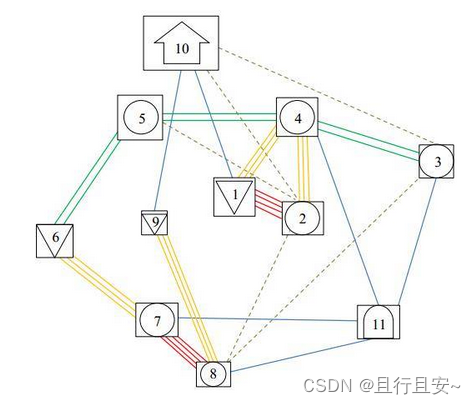
3.结果展示
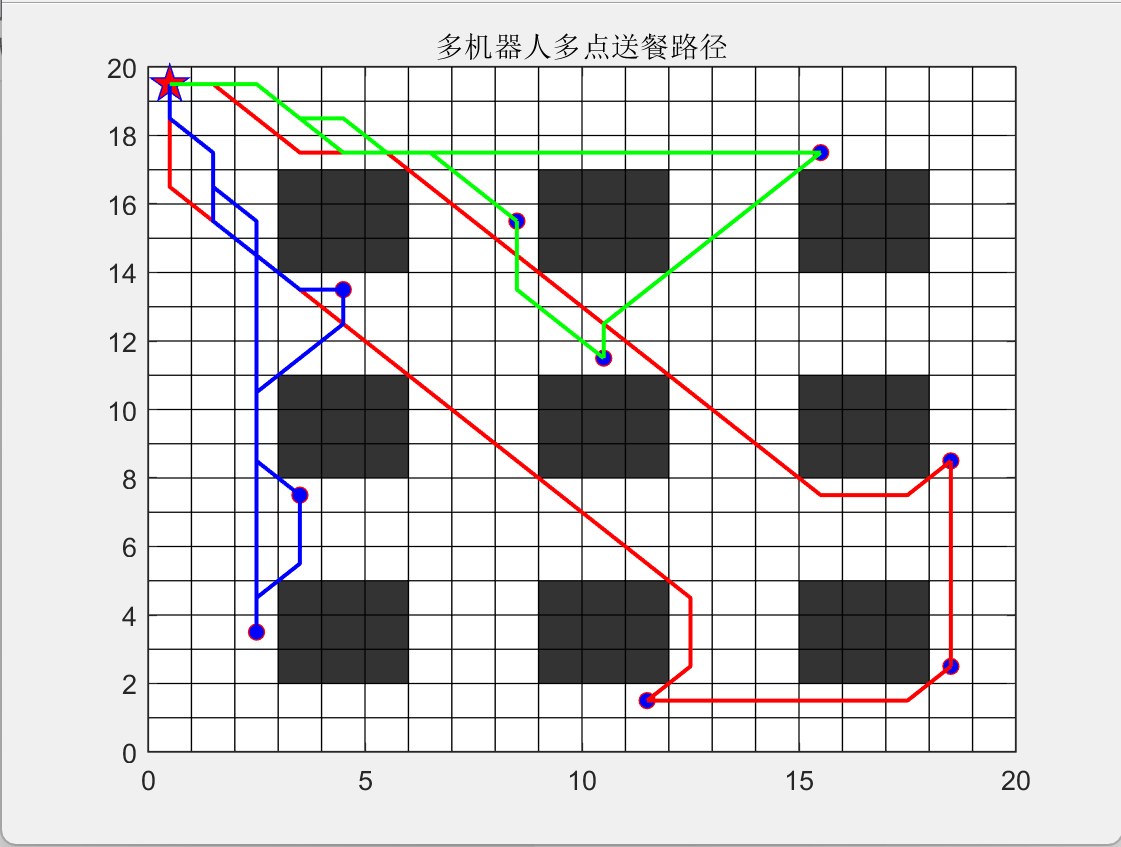
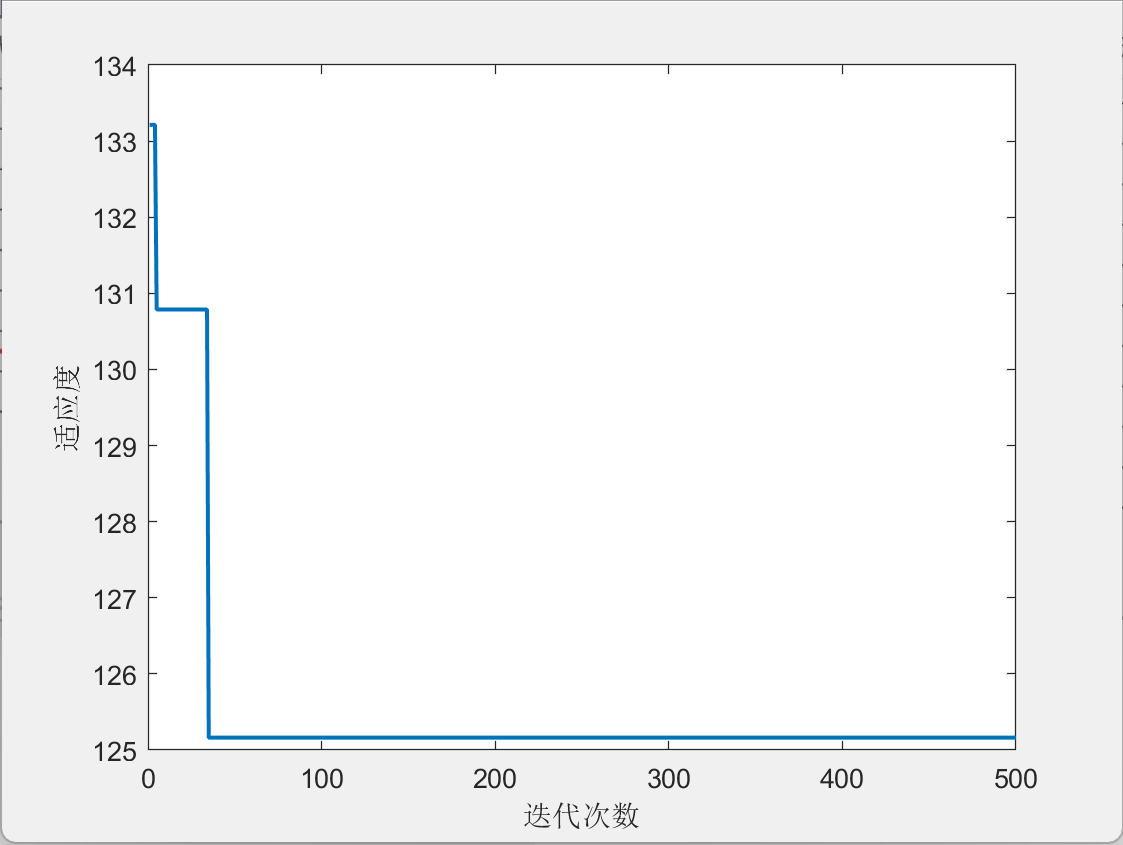
4.参考文献
[1] 蔡军,钟志远.改进蚁群算法的送餐机器人路径规划[J].智能系统学报,2024,19(02):370-380.
[2] 汪繁荣,杜力,徐光辉.基于改进蚁群算法的分布式多机器人协同路径规划[J].中南民族大学学报(自然科学版),2023,42(05):650-657.
5.代码获取
相关文章:

【智能算法应用】基于混合粒子群-蚁群算法的多机器人多点送餐路径规划问题
目录 1.算法原理2.数学模型3.结果展示4.参考文献5.代码获取 1.算法原理 【智能算法】粒子群算法(PSO)原理及实现 配餐顺序: 采用混合粒子群算法 || 路径规划: 采用蚁群算法 2.数学模型 餐厅送餐多机器人多点配送路径规划&…...

Java中的JVM调优技巧
Java中的JVM调优技巧 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! Java虚拟机(JVM)是Java应用程序的核心组件,负责将Jav…...

软件工程-第4章结构化编码和测试
软件的实现阶段:软件编码,单元测试和综合测试。 软件编码是对软件设计的进一步具体化,其任务是将设计表示变换成用程序设计语言编写的程序。 软件测试是软件质量保证的重要手段,要成功开发出高质量的软件产品,必须认…...
MMDetection 目标检测 —— 环境搭建和基础使用
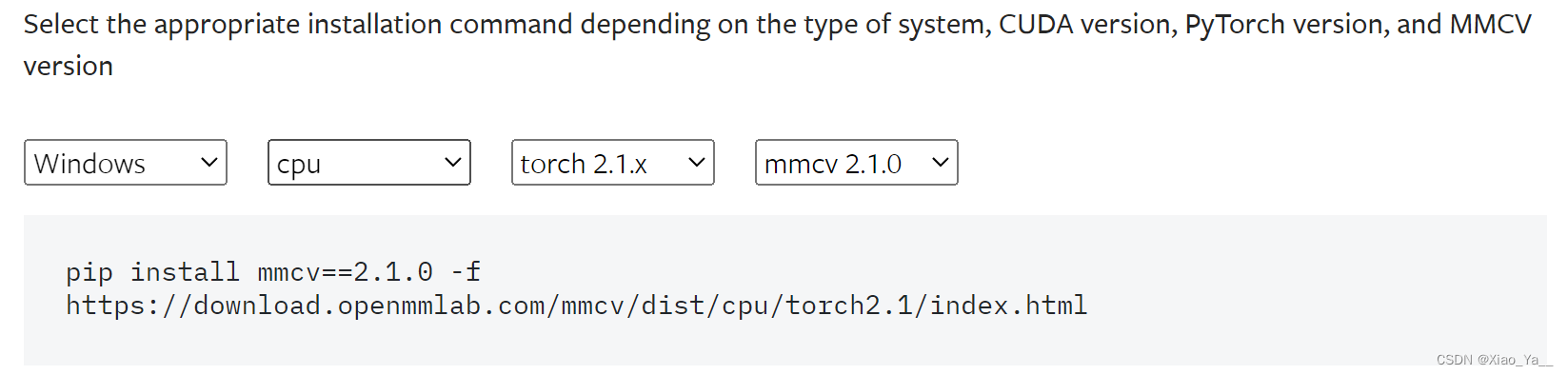
参考文档 开始你的第一步 — MMDetection 3.3.0 文档 依赖 步骤 0. 下载并安装 Anaconda。 步骤 1. 创建并激活一个 conda 环境。(我选择的是python3.10) conda create --name openmmlab python3.8 -y conda activate openmmlab 步骤 2. 基于 PyTo…...
C# 实现draw一个简单的温度计
运行结果 概述: 代码分析 该控件主要包含以下几个部分: 属性定义: MinValue:最低温度值。 MaxValue:最高温度值。 CurrentValue:当前温度值。 构造函数: 设置了一些控件样式来提升绘制效果…...

解放双手,让流程自动化软件助你一臂之力
本文将介绍流程自动化软件/脚本/助手的用途,同时我也做个自我介绍: 🏆 技术专长:专注于自动化脚本、网站、小程序、软件、爬虫及数据采集的定制化开发,为客户提供全方位的数字化解决方案。 💼 行业经验&…...

邀请函 | 桥田智能出席AMTS展会 家族新成员正式发布
作为国际汽车制造技术与装备及材料专业展览会,AMTS将于2024年7月3-5日在上海新国际博览中心举行。本届展会以【向“新”而行 “智”领未来】为主题,聚焦汽车及新能源全产业链,围绕“车身工程、部件工程、新能源三电工程及未来汽车开发”等技…...
安卓开发使用proxyman监控真机
1、真机跟电脑连接到同个网络中 2、手机里面设置代理,代理地址为proxyman上面指示的地址。 3、一般情况下,电脑的对应的端口是没开放的。需要到防火墙里面新建规则。入站规则 选择端口输入上方端口号 这样就能监控到了...

ruoyi登录功能源码分析
Ruoyi登录功能源码分析 上一篇文章我们分析了一下若依登录验证码生成的代码,今天我们来分析一下登录功能的代码 1、发送登录请求 前端通过http://localhost/dev-api/login向后端发送登录请求并携带用户的登录表单 在后端中的com.ruoyi.web.controller.system包下…...

推动产业数字化转型,六个方面引领变革
从工业经济时代走向数字经济时代,世界经济发生着全方位、革命性的变化,产业数字化便是最显著的表现之一。当前,产业数字化不断深入发展,平台经济、工业互联网、智能制造等新业态、新模式不断涌现,成为了数字经济的重要…...
设施布置之车间布局优化SLP分析
一 物流分析(Flow Analysis) 的基本方法 1、当物料移动是工艺过程的主要部分时,物流分析就是工厂布置设计的核心工作,也是物料搬运分析的开始。 2、零部件物流是该部件在工厂内移动时所走过的路线, 物流分析不仅要考虑…...

帕金森的锻炼方式
帕金森病,这个看似陌生的名词,其实离我们并不遥远。它是一种常见的神经系统疾病,影响着许多中老年人的生活质量。虽然帕金森病目前尚无根治之法,但通过科学合理的日常锻炼,可以有效缓解病情,提高生活质量。…...
模型训练过程)
PyTorch(一)模型训练过程
PyTorch(一)模型训练过程 #c 总结 实践总结 该实践从「数据处理」开始到最后利用训练好的「模型」预测,感受到了整个模型的训练过程。其中也有部分知识点,例如定义神经网络,只是初步的模仿,有一个比较浅的…...

windows下cmd命令行模式中cd变换路径命令无效的解决办法
一,出现的情况 二,解决方法 当出现转换盘的时候打开 cmd 之后可能是无法生效的 ,因为在cmd 中转换盘首先需要用到换盘符 。 Solve1 : 先进行换盘 C: c: // 转换到 C盘 D: d: // 转化到 D盘 Solve2 : 直接进行强转 cd /dE:\ACM算法资源\XCP…...

收藏||电商数据采集流程||电商数据采集API接口
商务数据分析的流程 第一步:明确分析目的。首先要明确分析目的,并把分析目的分解成若干个不同的分析要点,然后梳理分析思路,最后搭建分析框架。 第二步:数据采集。主流电商API接口数据采集,一般可以通过数…...

修改源码,打patch包,线上环境不生效
1.首先看修改的源码文件是否正确 在node_modules中,找对应的包,然后查看包中package.json 的main和module。如果用require引入,则修改lib下面的组件,如果是import引入则修改es下面的文件 main 对应commonjs引入方式的程序入口文件…...

NUC980-OLED实现全中文字库的方法
1.背景 有一个产品,客户需要屏幕展示一些内容,要带一些中文,实现了OLED12864的驱动,但是它不带字库,现在要实现OLED全字库的显示 2.制作原始字库 下载软件pctolcd2002 设置 制作字库 打开原始文件 用软件自带的&…...

UEFI 启动原理及qemu 虚拟化中使用
UEFI 启动原理及qemu 虚拟化中使用 什么是BIOS?什么是 UEFI? 什么是BIOS? 计算机启动时会加载 BIOS,以初始化和测试硬件功能。它使用 POST 或 Power On Self Test 来确保硬件配置有效且工作正常,然后寻找存储引导设…...

35、正则表达式
一、正则表达式命令 正则表达式:匹配的是文本内容,linux的文本三剑客都是针对文本内容。 grep 过滤文本内容 sed 针对文本内容进行增删改查 awk 按行取列 文本三剑客----都是按照行进行匹配。 1.1、grep筛选: grep的作用就是…...

Ubuntu20.04中复现FoundationPose
Ubuntu20.04中复现FoundationPose 文章目录 Ubuntu20.04中复现FoundationPose1.安装cuda和cudnn2.下载相关资源3.环境配置4.运行model-based demo5.运行ycbv demoReference 🚀 非常重要的环境配置 🚀 ubuntu 20.04cuda 11.8.0cudnn v8.9.7python 3.9.19…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
