数据结构篇:旋转操作在AVL树中的实现过程
本节课在线学习视频(网盘地址,保存后即可免费观看):
https://pan.quark.cn/s/06d5ed47e33b
AVL树是平衡二叉搜索树的一种,它通过旋转操作来保持树的平衡。AVL树的特点是,任何节点的两个子树的高度最大差别为1。本文将详细介绍AVL树中的旋转操作及其实现过程,并通过多个代码案例来说明这些操作的应用。
1. AVL树的基本概念
AVL树是一种自平衡二叉搜索树,其核心思想是通过旋转操作来维持树的平衡。旋转操作有四种:左旋、右旋、左右旋和右左旋。旋转操作的目的是调整树的结构,使其保持平衡,从而保证二叉搜索树的性能。
平衡因子
平衡因子是指某个节点的左子树高度减去右子树高度的值。AVL树的每个节点的平衡因子只能是-1、0或1。
2. 旋转操作
2.1 右旋(Right Rotation)
右旋是对某个节点进行的单次旋转,使得该节点的左子树成为其父节点。
案例1:右旋操作
class AVLNode {int val;int height;AVLNode left;AVLNode right;AVLNode(int val) {this.val = val;this.height = 1;}
}public class AVLTree {private int height(AVLNode node) {if (node == null) return 0;return node.height;}private AVLNode rightRotate(AVLNode y) {AVLNode x = y.left;AVLNode T2 = x.right;x.right = y;y.left = T2;y.height = Math.max(height(y.left), height(y.right)) + 1;x.height = Math.max(height(x.left), height(x.right)) + 1;return x;}public static void main(String[] args) {AVLTree tree = new AVLTree();AVLNode root = new AVLNode(30);root.left = new AVLNode(20);root.left.left = new AVLNode(10);root = tree.rightRotate(root);System.out.println("After right rotation, root is: " + root.val);}
}在这个例子中,我们对根节点进行了右旋操作,使其左子树成为新的根节点。
2.2 左旋(Left Rotation)
左旋是对某个节点进行的单次旋转,使得该节点的右子树成为其父节点。
案例2:左旋操作
class AVLTree {// 同上private AVLNode leftRotate(AVLNode x) {AVLNode y = x.right;AVLNode T2 = y.left;y.left = x;x.right = T2;x.height = Math.max(height(x.left), height(x.right)) + 1;y.height = Math.max(height(y.left), height(y.right)) + 1;return y;}public static void main(String[] args) {AVLTree tree = new AVLTree();AVLNode root = new AVLNode(10);root.right = new AVLNode(20);root.right.right = new AVLNode(30);root = tree.leftRotate(root);System.out.println("After left rotation, root is: " + root.val);}
}在这个例子中,我们对根节点进行了左旋操作,使其右子树成为新的根节点。
2.3 左右旋(Left-Right Rotation)
左右旋是对某个节点进行的两次旋转:先对其左子树进行左旋,再对该节点进行右旋。
案例3:左右旋操作
class AVLTree {// 同上private AVLNode leftRightRotate(AVLNode node) {node.left = leftRotate(node.left);return rightRotate(node);}public static void main(String[] args) {AVLTree tree = new AVLTree();AVLNode root = new AVLNode(30);root.left = new AVLNode(10);root.left.right = new AVLNode(20);root = tree.leftRightRotate(root);System.out.println("After left-right rotation, root is: " + root.val);}
}在这个例子中,我们对根节点进行了左右旋操作,先对其左子树进行左旋,再对根节点进行右旋。
2.4 右左旋(Right-Left Rotation)
右左旋是对某个节点进行的两次旋转:先对其右子树进行右旋,再对该节点进行左旋。
案例4:右左旋操作
class AVLTree {// 同上private AVLNode rightLeftRotate(AVLNode node) {node.right = rightRotate(node.right);return leftRotate(node);}public static void main(String[] args) {AVLTree tree = new AVLTree();AVLNode root = new AVLNode(10);root.right = new AVLNode(30);root.right.left = new AVLNode(20);root = tree.rightLeftRotate(root);System.out.println("After right-left rotation, root is: " + root.val);}
}在这个例子中,我们对根节点进行了右左旋操作,先对其右子树进行右旋,再对根节点进行左旋。
3. AVL树的插入操作
AVL树的插入操作需要在插入新节点后,检查节点的平衡因子,并根据平衡因子进行相应的旋转操作,以保持树的平衡。
案例5:AVL树的插入操作
public class AVLTree {// 同上private int balanceFactor(AVLNode node) {if (node == null) return 0;return height(node.left) - height(node.right);}public AVLNode insert(AVLNode node, int val) {if (node == null) return new AVLNode(val);if (val < node.val) node.left = insert(node.left, val);else if (val > node.val) node.right = insert(node.right, val);else return node;node.height = 1 + Math.max(height(node.left), height(node.right));int balance = balanceFactor(node);if (balance > 1 && val < node.left.val) return rightRotate(node);if (balance < -1 && val > node.right.val) return leftRotate(node);if (balance > 1 && val > node.left.val) {node.left = leftRotate(node.left);return rightRotate(node);}if (balance < -1 && val < node.right.val) {node.right = rightRotate(node.right);return leftRotate(node);}return node;}public static void main(String[] args) {AVLTree tree = new AVLTree();AVLNode root = null;int[] values = {10, 20, 30, 40, 50, 25};for (int val : values) {root = tree.insert(root, val);}System.out.println("AVL Tree constructed successfully.");}
}在这个例子中,我们实现了AVL树的插入操作。每次插入新节点后,我们检查平衡因子,并通过旋转操作保持树的平衡。
4. 注意事项
- 在进行旋转操作时,需要同时更新节点的高度和子树的高度。
- 插入和删除操作可能会导致多个节点的平衡因子变化,需要从插入或删除位置向上逐层检查和调整。
- 在实现AVL树时,确保所有旋转操作的逻辑正确,以避免树的不平衡或错误的结构。
结语
本文详细介绍了AVL树中的旋转操作及其实现过程,包括右旋、左旋、左右旋和右左旋。通过多个代码案例,我们展示了这些旋转操作的应用和效果。在实际开发中,AVL树通过旋转操作保持平衡,从而保证二叉搜索树的高效性能。希望这些示例和注意事项能帮助你更好地理解和应用AVL树中的旋转操作。
相关文章:

数据结构篇:旋转操作在AVL树中的实现过程
本节课在线学习视频(网盘地址,保存后即可免费观看): https://pan.quark.cn/s/06d5ed47e33b AVL树是平衡二叉搜索树的一种,它通过旋转操作来保持树的平衡。AVL树的特点是,任何节点的两个子树的高度最大差别…...

为什么Java默认使用UTF-16,Golang默认使用UTF-8呢?
Java 和 Go 语言在默认字符编码上做出了不同的选择,这是由它们的设计目标和使用场景决定的。下面是对 Java 默认使用 UTF-16 和 Go 默认使用 UTF-8 的原因进行的详细解释。 Java 默认使用 UTF-16 的原因 1. 历史背景和兼容性 Unicode 的发展: Java 诞生于 1995 年…...
)
JavaScript常见面试题(三)
文章目录 1.对原型、原型链的理解2.原型修改、重写3.原型链指向4.对闭包的理解5. 对作用域、作用域链的理解6.对执行上下文的理解7.对this对象的理解8. call() 和 apply() 的区别?9.异步编程的实现方式?10.setTimeout、Promise、Async/Await 的区别11.对…...

【Effective Modern C++】第1章 型别推导
【Effective Modern C】第1章 型别推导 文章目录 【Effective Modern C】第1章 型别推导条款1:理解模板型别推导基础概念模板型别推导的三种情况情景一 ParamType 是一个指针或者引用,但非通用引用情景二 ParamType是一个通过引用情景三 ParamType既不是…...
服装连锁实体店bC一体化运营方案
一、引言 随着互联网的快速发展和消费者购物习惯的变化,传统服装连锁实体店在面对新的市场环境下亟需转型升级。BC(Business to Consumer)一体化运营方案的实施将成为提升服装连锁实体店竞争力和顾客体验的关键举掖。商淘云详细介绍服装连锁…...
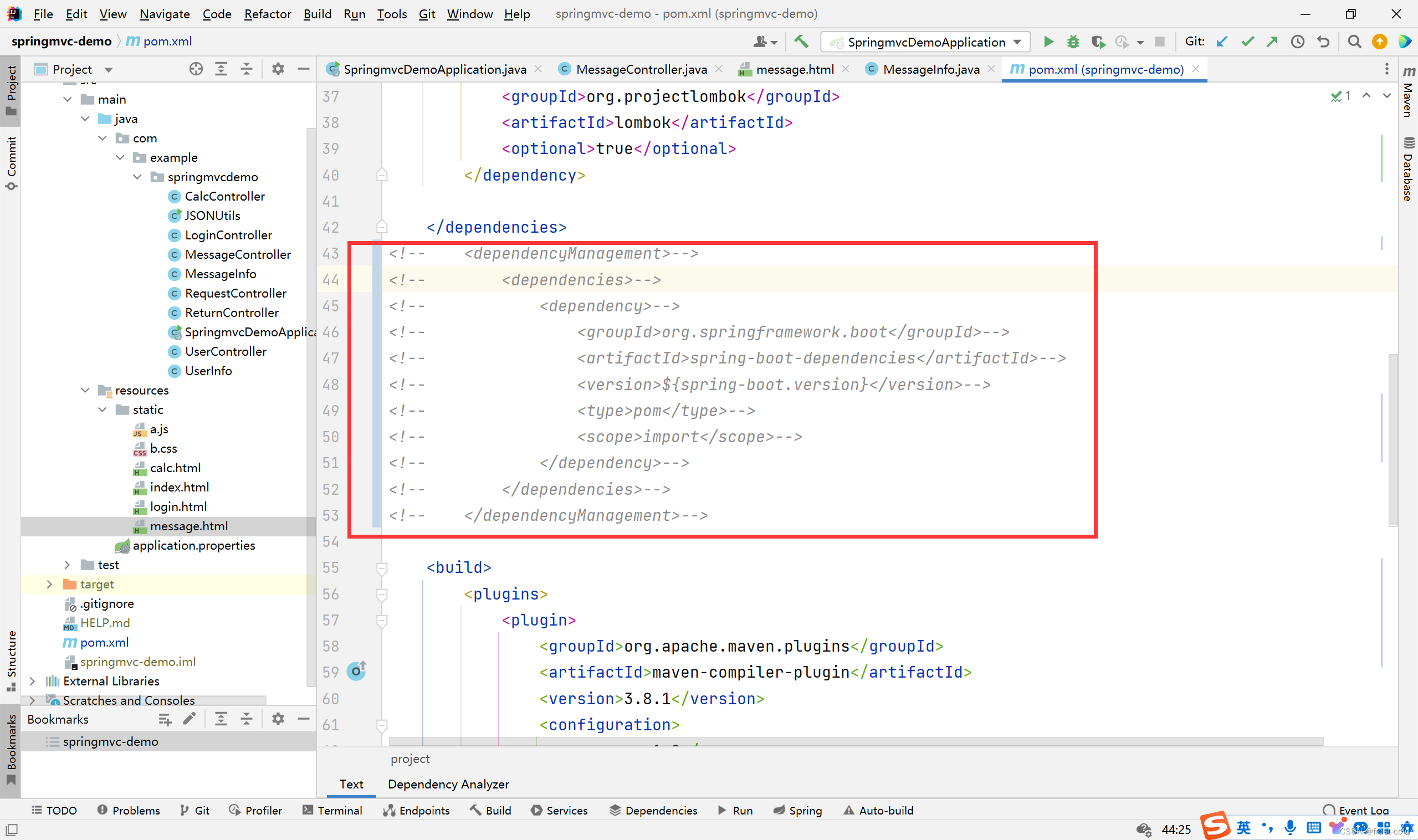
IDEA中SpringMVC的运行环境问题
文章目录 一、IEAD 清理缓存二、用阿里云和spring创建 SpringMVC 项目中 pom.xml 文件的区别 一、IEAD 清理缓存 springMVC 运行时存在一些之前运行过的缓存导致项目不能运行,可以试试清理缓存 二、用阿里云和spring创建 SpringMVC 项目中 pom.xml 文件的区别 以下…...

Python初体验
# Java基础知识学的差不多了,项目上又没什么事,学学py,方便以后对接 1、打包flask应用(好痛苦,在什么平台打包就只在那个平台可用想在linux用只能参考方法2了) pyinstaller --onefile app.py -n myapp 2…...

从零开始如何学习人工智能?
说说我自己的情况:我接触AI的时候,是在研一。那个时候AlphaGo战胜围棋世界冠军李世石是大新闻,人工智能第一次出现我面前,当时就想搞清楚背后的原理以及这些技术有什么作用。 就开始找资料,看视频。随着了解的深入&am…...

【仿真建模-anylogic】动态生成ConveyorCustomStation
Author:赵志乾 Date:2024-06-18 Declaration:All Right Reserved!!! 0. 背景 直接使用Anylogic组件开发的模型无法动态改变运输网布局;目前需求是要将运输网布局配置化;运输网配置化…...
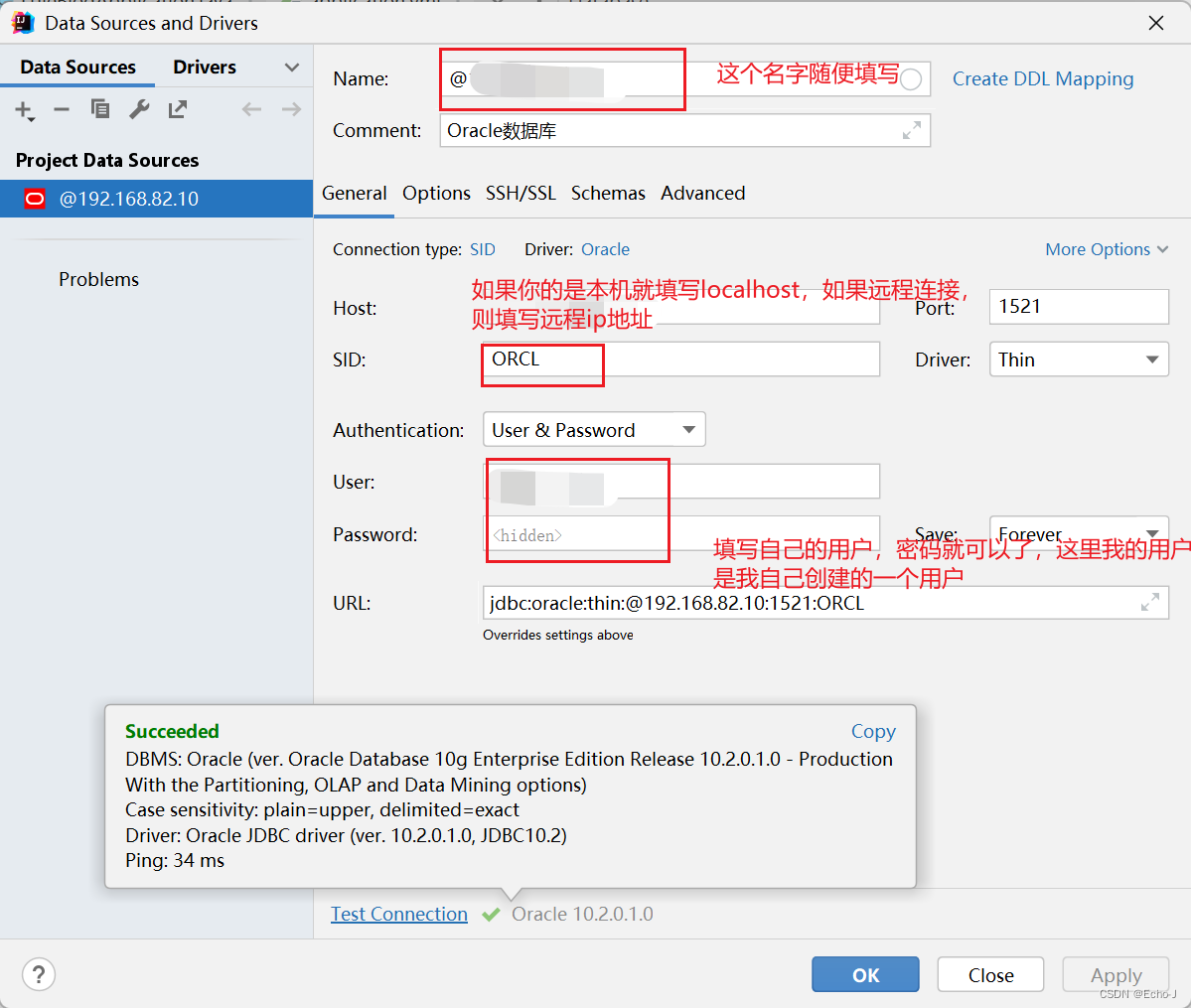
如何使用idea连接Oracle数据库?
idea版本:2021.3.3 Oracle版本:10.2.0.1.0(在虚拟机Windows sever 2003 远程连接数据库) 数据库管理系统:PLSQL Developer 在idea里面找到database,在idea侧面 选择左上角加号,新建ÿ…...

谈谈kafaka的并行处理,顺带讲讲rabbitmq
简介 Kafka 是一个分布式流处理平台,它支持高效的并行处理。Kafka 的并行处理能力主要体现在以下几个方面: 分区(Partition)并行 Kafka 将数据存储在称为"分区"的逻辑单元中。每个分区可以独立地并行地进行读写操作。生产者可以根据分区策略,将数据写入到指定的分…...

P3056 [USACO12NOV] Clumsy Cows S
[USACO12NOV] Clumsy Cows S 题目描述 Bessie the cow is trying to type a balanced string of parentheses into her new laptop, but she is sufficiently clumsy (due to her large hooves) that she keeps mis-typing characters. Please help her by computing the min…...

智赢选品,OZON数据分析选品利器丨萌啦OZON数据
在电商行业的激烈竞争中,如何快速准确地把握市场动态、洞察消费者需求、实现精准选品,是每个电商卖家都面临的挑战。而在这个数据驱动的时代,一款强大的数据分析工具无疑是电商卖家们的得力助手。今天,我们就来聊聊这样一款选品利…...

Canal自定义客户端
一、背景 在Canal推送数据变更信息至MQ(消息队列)时,我们遇到了特定问题,尤其是当消息体的大小超过了MQ所允许的最大限制。这种限制导致数据推送过程受阻,需要相应的调整或处理。 二、解决方法 采用Canal自定义客户…...
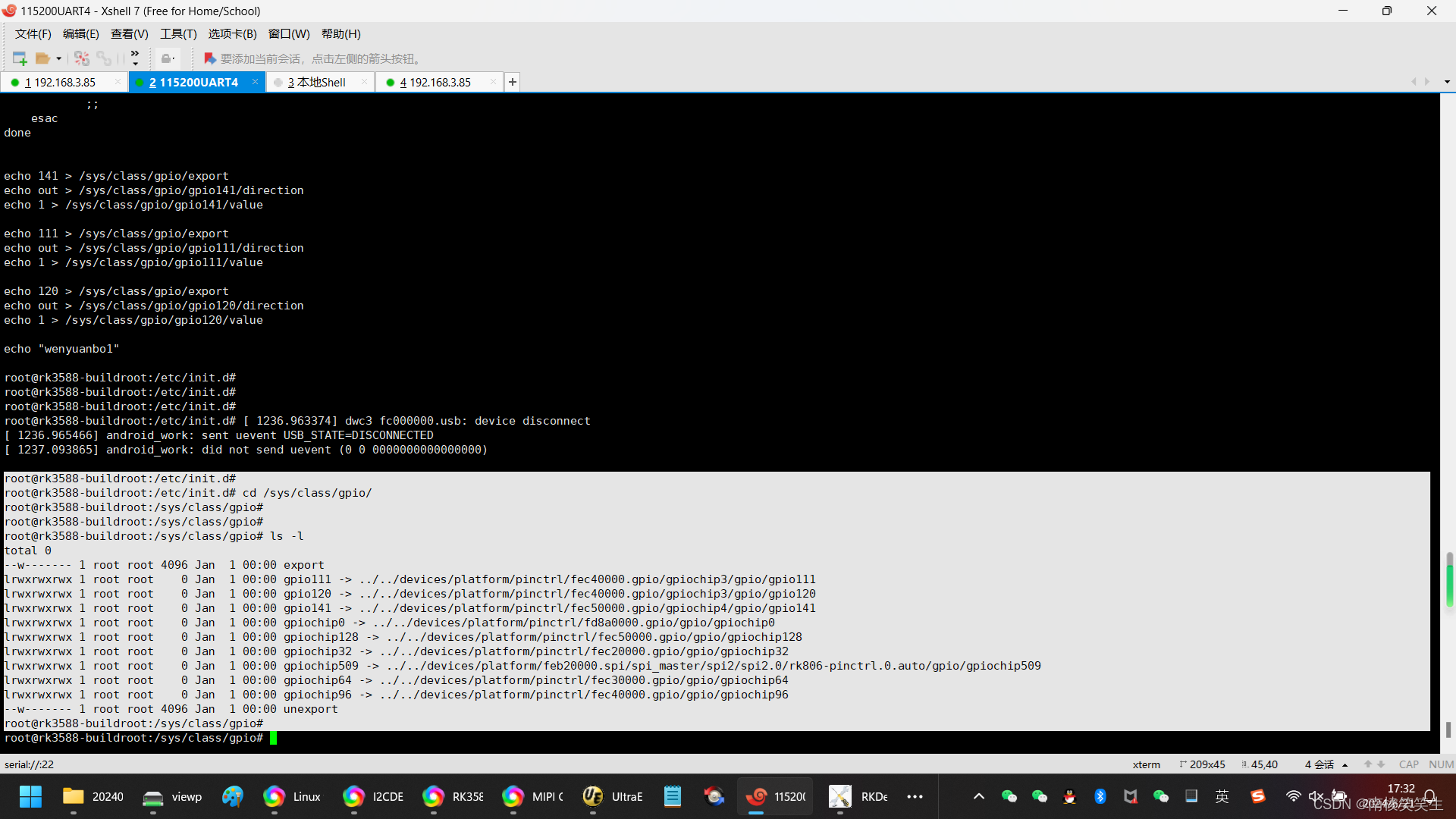
20240621将需要自启动的部分放到RK3588平台的Buildroot系统的rcS文件中
20240621将需要自启动的部分放到RK3588平台的Buildroot系统的rcS文件中 2024/6/21 17:15 开发板:飞凌OK3588-C SDK:Rockchip原厂的Buildroot 缘起:在凌OK3588-C的LINUX R4系统启动的时候,需要拉高GPIO4_B5、GPIO3_B7和GPIO3_D0。…...
掌握数据魔方:Xinstall引领ASA全链路数据归因新纪元
一、引言 在数字化时代,数据是App推广和运营的核心驱动力。然而,如何准确获取、分析并应用这些数据,却成为了许多开发者和营销人员面临的痛点。Xinstall作为一款专业的App全渠道统计服务商,致力于提供精准、高效的数据解决方案&a…...

IIS代理配置-反向代理
前后端分离项目,前端在开发中使用proxy代理解决跨域问题,打包之后无效。 未配置前无法访问 部署环境为windows IIS,要在iis设置反向代理 安装代理模块 需要在iis中实现代理,需要安装Application Request Routing Cache和URL重…...
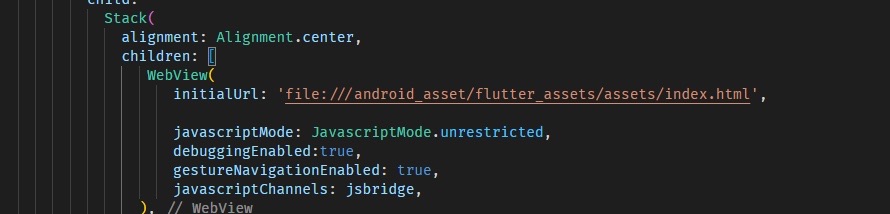
Flutter调用本地web
前言: 在目前Flutter 环境中,使用在线 webview 是一种很常见的行为 而在 app 环境中,离线使用则更有必要 1.环境准备 将依赖导入 2.引入前端代码 前端代码有两种情况 一种是使用打包工具 build 而来的前端代码 另一种情况是直接使用 HTML 文件 …...

AI大模型部署Ubuntu服务器攻略
一、下载Ollama 在线安装: 在linux中输入命令curl -fsSL https://ollama.com/install.sh | sh 由于在linux下载ollama需要经过外网,网络会不稳定,很容易造成连接超时的问题。 离线安装: 步骤一: 下载Ollama离线版本…...

vlan、vxlan、vpc学习
文章目录 前言VLAN (Virtual Local Area Network)定义工作原理优点应用场景限制 VXLAN (Virtual eXtensible Local Area Network)工作原理优点应用场景与VLAN的区别 VPC (Virtual Private Cloud)定义特点优势应用场景与VLAN/VXLAN的关联 总结 前言 VLAN(Virtual Lo…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
