数据结构【二叉树】
前言
我们在前面学习了使用数组来实现二叉树,但是数组实现二叉树仅适用于完全二叉树(非完全二叉树会有空间浪费),所以我们本章讲解的是链式二叉树,但由于学习二叉树的操作需要有一颗树,才能学习相关的基本操作,由于这只是开头,为了降低学习的成本,所以我们手动的来创建一颗普通的二叉树,等到本文的后面,再讲解真正的创建
二叉树的基本结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;创建新结点
BTNode*BuyNode(BTDataType x)
{BTNode* Node = (BTNode*)malloc(sizeof(BTNode));if (Node == NULL){perror("malloc fail:");exit(1);}Node->_data = x;Node->_left = Node->_right = NULL;
}创造树
BTNode* CreateBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);BTNode* node8 = BuyNode(8);node1->_left = node2;node2->_left = node3;node3->_right = node4;node1->_right = node5;node5->_right = node6;node6->_left = node7;node6->_right = node8;return node1;
}int main()
{BTNode* root = CreateBinaryTree();return 0;
}
最后效果如图
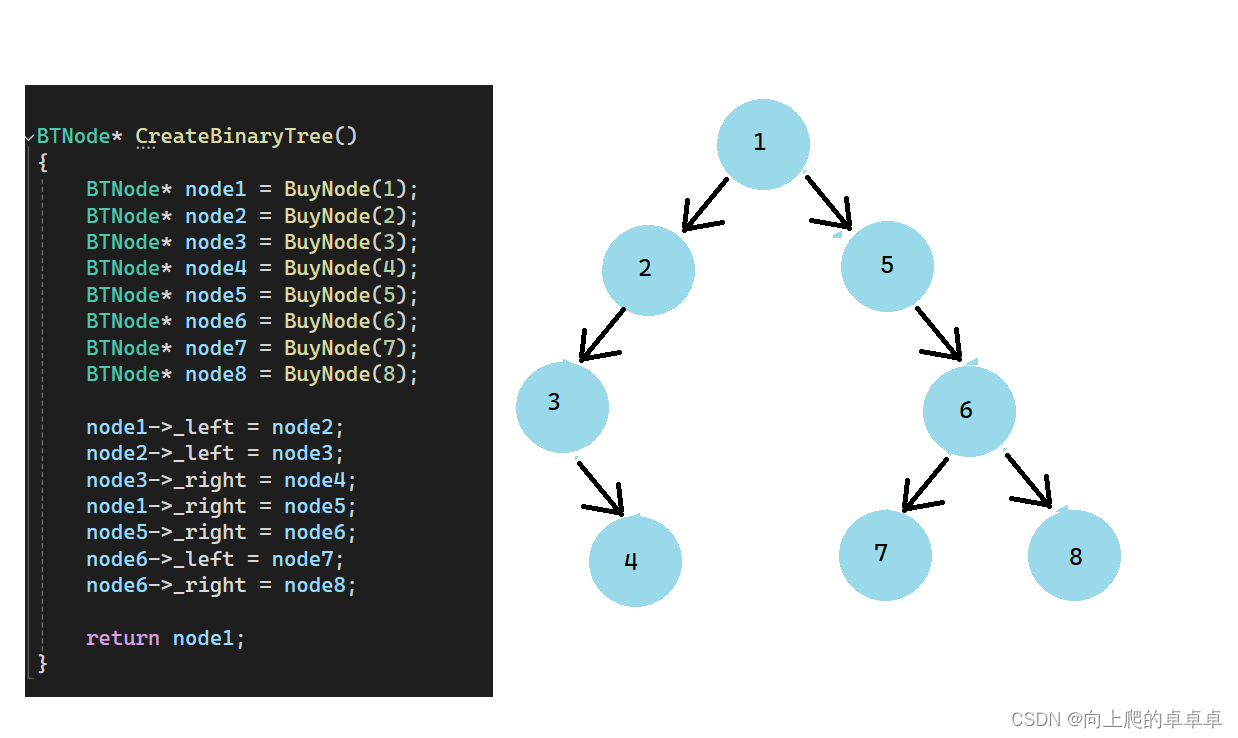
在完成二叉树的基本操作之前,我们先在这里简单的回顾一下二叉树的基本概念。
二叉树只有两个状态
- 空树
- 非空:由根结点,根节点的左子树,根结点的右子树组成

从图中可以看出,二叉树定义是递归形式的(根结点的左孩子也能看作根,其左右孩子以及对于的联系也能看成左右子树,根的右孩子同理),所以我们下面的操作都是通过递归来实现。
以下所有的操作都会使用上面手搓的树
二叉树的遍历
所谓前中后序的遍历就是根结点的先后访问顺序,所以前中后序遍历也叫前根、中根、后根遍历。
- 前序(前根)的访问顺序:根、左子树、右子树
- 中序(中根)的访问顺序:左子树、根、右子树
- 后序(后根)的访问顺序:左子树、右子树、根
这里先将遍历的原因是后续的操作,都会用到遍历的思路。

前序遍历
一般说这个树的前序遍历是[1, 2, 3, 4, 5, 6, 7, 8]
但这不是最详细的表达,最详细的表达是[1, 2, 3, NULL, 4, NULL, NULL, NULL, 5, NULL, 6, 7, NULL, NULL, 8, NULL, NULL]。
3 后面的
NULL其实是 3 的左孩子,4 后面俩个NULL代表的是 4 的左孩子和右孩子,而 5 前面的NULL代表的是 2 的右孩子,5 后面的NULL代表 5 的左孩子,7 和 8 后面的NULL都是代表他们的左右孩子。
中序
一般说这个树的中序遍历是[3, 4, 2, 1, 5, 7, 6, 8 ];
实际则是[N, 3, N, 4, N, 2, N, 1, N, 5, N, 7, N, 6, N, 8, N](N代替NULL)
由于是先访问左子树,所以第一个真正被遍历的一定是NULL。
3 前面的
N就是 3 的左孩子,4 前后的N则代表的是 4 的左右孩子,2 后面的N代表的是 2 的右孩子;5 前面的N代表 5 的左孩子,7 和 8 前后的N都代表他们的左右孩子。
后序
一般:[4, 3, 2, 7, 8, 6, 5, 1]
实际则是[N, N, N, 4, 3, N, 2, N, N, N, 7, N, N, 8, 6, 5, 1](N代替NULL)
第一个
N是 3 的左孩子,第二第三个N是 4 的左右孩子,3 后面的N是 2 的右孩子;而 2 后面的第一个N是 5 的左孩子,7 和 8 的前俩个N都是代表他们的左右孩子
注意:无论是哪种遍历,孩子之间的顺序一定是先左孩子,再是右孩子。
层序遍历
就是我们正常的思维,一层一层、从左到右的依次遍历,这种遍历方式叫广度优先遍历(BFS),而前三种遍历方式叫深度优先遍历(DFS)。
层序遍历需要依靠队列来实现。
代码实现
前中后序的遍历的大体相同,只是打印的位置不同
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}前序时printf的位置在前面printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);中序时printf的位置在中间printf("%d ", root->_data);BinaryTreePrevOrder(root->_right);后续时printf的位置在末尾printf("%d ", root->_data);
}
用图像讲解递归过程

右子树的递归过程大体相同,注意实际情况并不会开那么多的空间,而是当你使用完返回再使用的时候,是将原来的空间给重新利用了。
层序遍历的实现
在完成层序遍历之前,我们需要有队列这个数据结构(我们可以直接将以前的代码拿过来:具体代码在数据结构【队列】)
具体思路是,先创建一个队列,将二叉树的根结点存放到队列里,每遍历一个结点就删掉这个在队列里的结点,删掉的同时,将该结点的左右孩子存放到队列内部这样依次往复。
这里的类型是结点的类型,并且存放的是指针,所以要带个*号
typedef struct BinaryTreeNode* QUEUEDATA;typedef struct QNode
{QUEUEDATA _val;struct QNode* _next;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
层序遍历代码
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue* q = (Queue*)malloc(sizeof(Queue));QueueInit(q);//先把root入到队列QueuePush(q, root);//当队列尾空时,就代表以及打印完了while (!QueueEmpty(q)){//取队头数据BTNode*tmp = QueueFirst(q);//然后删除数据,我只是操作队列内部,并没有动原来的二叉树QueuePop(q);//当为空时不加数据,这就能应对根结点是空时的情况,就不需要在外面再做一次判断if (tmp == NULL){printf("N ");}//非空,将左右孩子添加到队列else{printf("%d ", tmp->_data);QueuePush(q,tmp->_left);QueuePush(q,tmp->_right);}}
}
二叉树的计算
本文计算关于树的计算有四个
- 计算树结点的个数
- 计算树的叶子结点个数
- 计算第k层的节点个数
- 计算树的高度
计算节点个数
这就很简单了,就是左右子树加自己,但每个孩子又可以分为根,左子树,右子树,当根等于空时返回0就可以了。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
这里的+1就是加自己,当你来到下面那个return时,就代表该节点并不是空节点。
计算叶子节点个数
简单的回顾一下:叶子节点就是左右孩子都为空的节点。
所以就可以判断当左右孩子都为空时,就返回 1。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
计算第k层节点个数
这个也能很好的用递归来解决,第k层是对于根节点来说的,但对于根节点的下一层来说,第k层其实是第k-1层,所以可以一直减下去,直到当k==1时,return 1。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
计算树的高度
那我就比较左子树和右子树的高度,比较出结果后再加自身的高度(比较出的高度+1)
结束递归的条件就是当我的子树为空,返回0。
// 二叉树的高度
int BinaryHeight(BTNode* root)
{if (root == NULL){return 0;}return BinaryHight(root->_left) > BinaryHight(root->_right) ? BinaryHight(root->_left) + 1: BinaryHight(root->_right) + 1;
}
这样也可以,但是如果用这个去做利扣的题是无法通过的,并不是因为程序结果错误,而是因为栈溢出。
看看为什么会栈溢出:我要比较出两个子树的长度,就一定会运行
return BinaryHight(root->_left) > BinaryHight(root->_right) ? BinaryHight(root->_left) + 1: BinaryHight(root->_right) + 1; 这有没有发现,我并没有记录比较高的值,我辛辛苦苦递归很多次才得到的左右子树中较高的子树,当我要返回高度的时候,诶?我前面的数是啥?所以我就又要进行 BinaryHight(root->_left) + 1或者BinaryHight(root->_right) + 1,这样我又会进行递归,再递归比较,然后再递归返回值->递归比较这样一直下去,直到最低层(root == NULL)。
所以,我们需要变量来记录两颗子树的高度,这样我们再比较的时候就不会重复递归了。
// 二叉树的高度
int BinaryHeight(BTNode* root)
{if (root == NULL){return 0;}//记录左树的高度int L = BinaryHight(root->_left);//记录右树的高度int R = BinaryHight(root->_right);//比较出较高的,加上自己这一层的高度return (L > R ? L : R) + 1;
}
二叉树的创建和销毁
二叉树的创建(前序)
这题是使用前序来创建二叉树
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
'#'号代表空,a是数组,n是长度,pi是下标
先创建父亲节点,然后左子树 -> 创建左子树当中的父亲节点,然后创建左子树 —>直到这时的数据是'#'返回NULL,创建右子树,右子树创建完,函数自然结束,回到上一层让上一层来创建右子树。
当pi等于n的时候,就代表已经遍历完该数组了,这条数组里的数据已经被我创建成一个二叉树了;这时候就返回NULL;这个判断放在函数的开头。
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
//当下标与长度相等,返回NULLif (*pi == n){return NULL;}if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));//先创建根节点,再创建左子树,再创建右子树root->_data = a[(*pi)++];root->_left = BinaryTreeCreate(a, n, pi);//先创建左子树root->_right = BinaryTreeCreate(a, n, pi);//再创建右子树return root;//返回根节点
}
二叉树的销毁(后序)
这题我们采用后序来删除,是因为后续并不需要记录节点,是从底层一点一点销毁节点,当我左右子树的节点都销毁了(或者都为NULL),才销毁我的根节点。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
既然是销毁,那么就会修改原来的值,所以我们就传二叉树根节点的地址。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (root == NULL || *root == NULL){return;}BinaryTreeDestory(&(*root)->_left);//先销毁左子树BinaryTreeDestory(&(*root)->_right);//再销毁右子树//当左右节点都被销毁或者都为NULLfree(*root);//最后再销毁根节点
}
结语
到这里二叉树的基本函数就讲完啦。
最后感谢您能阅读完此片文章,如果有任何建议或纠正欢迎在评论区留言,也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获,点一个小小的赞就是我创作的巨大动力,谢谢!!!
相关文章:

数据结构【二叉树】
前言 我们在前面学习了使用数组来实现二叉树,但是数组实现二叉树仅适用于完全二叉树(非完全二叉树会有空间浪费),所以我们本章讲解的是链式二叉树,但由于学习二叉树的操作需要有一颗树,才能学习相关的基本…...

Vue P17-54
18、计算属性 示例:实现姓名的联动效果 可以用插值语法、method {{func()}} 这里必须有 ()表示返回值 在事件处理中,click“func1” 有没有无所谓 computed的计算属性和data中的属性都在vm中,但vm._data里只有后者…...

【自动驾驶】从零开始做自动驾驶小车
文章目录 自动驾驶小车系统、运动底盘的运动学分析和串口通信控制电机PID控制IMU初始化与陀螺仪零点漂移ubuntu基础教程ROS基础键盘控制巡线(雷达避障)雷达跟随视觉跟踪2D建图、2D导航3D建图、3D导航纯视觉建图导航语音控制KCF跟随自主建图建图与导航多机编队WEB浏览器显示摄像…...

一文让你彻底搞懂什么是VR、AR、AV、MR
随着科技的飞速发展,现实世界与虚拟世界的界限变得越来越模糊。各种与现实增强相关的技术如雨后春笋般涌现,令人眼花缭乱。本文将为你详细解读四种常见的现实增强技术:虚拟现实(VR)、增强现实(AR࿰…...
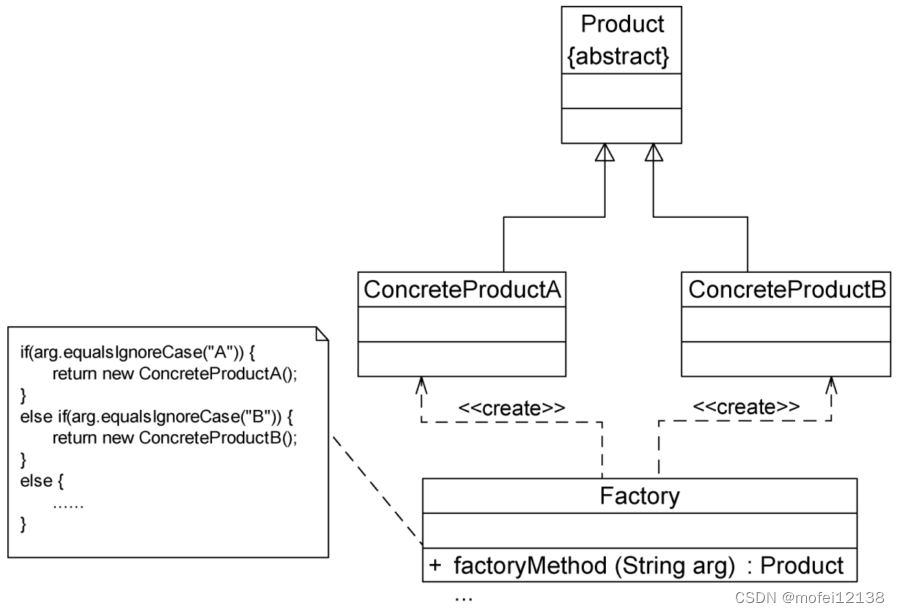
Python设计模式 - 简单工厂模式
定义 简单工厂模式是一种创建型设计模式,它通过一个工厂类来创建对象,而不是通过客户端直接实例化对象。 结构 工厂类(Factory):负责创建对象的实例。工厂类通常包含一个方法,根据输入参数的不同创建并返…...

L55--- 257.二叉树的所有路径(深搜)---Java版
1.题目描述 2.思路 (1)因为是求二叉树的所有路径 (2)然后是带固定格式的 所以我们要把每个节点的整数数值换成字符串数值 (3)首先先考虑根节点,也就是要满足节点不为空 返回递归的形式dfs(根节…...

智慧园区解决方案PPT(53页)
## 1.1 智慧园区背景及需求分析 - 智慧园区的发展历程包括园区规划、经济、产业、企业、管理、理念的转变,强调管理模式创新,关注业务综合化、管理智慧化等发展。 ## 1.2 国家对智慧园区发展的政策 - 涉及多个国家部门,如工信部、住建部、…...
)
Windows安装MySQL(8.0.37)
安装:https://blog.csdn.net/XLBYYDS/article/details/139711682 注意点: (1)必须安装到C盘系统盘,否则执行 net start mysql 启动服务时,可能会启动失败。 (2)如果安装时出现 The…...
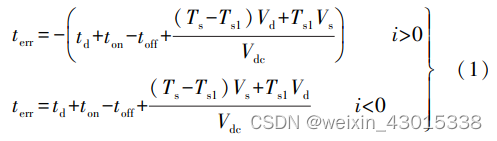
永磁同步电机驱动死区补偿
1 死区效应及补偿 1. 1 死区效应 在本文的电机控制嵌入式系统中,逆变器为三 相电压型桥式逆变电路,如图 1 所示。 在理想状态 下,上桥臂和下桥臂的控制信号满足互补通断原则, 即上桥臂开通时,下桥臂关断,反之亦然。 而在实际 应用中,开关管的通断需要一定的开通时…...

智能体合集
海外版coze: 前端代码助手 后端代码助手: 前端代码助手:...

智能农业管理系统设计
一、引言 随着物联网、云计算和大数据技术的快速发展,智能农业管理系统成为提高农业生产效率、优化资源配置、降低环境污染的重要手段。本设计旨在构建一个集数据采集、传输、处理、分析于一体的智能农业管理系统,为农业生产提供全方位、精准化的服务。 …...
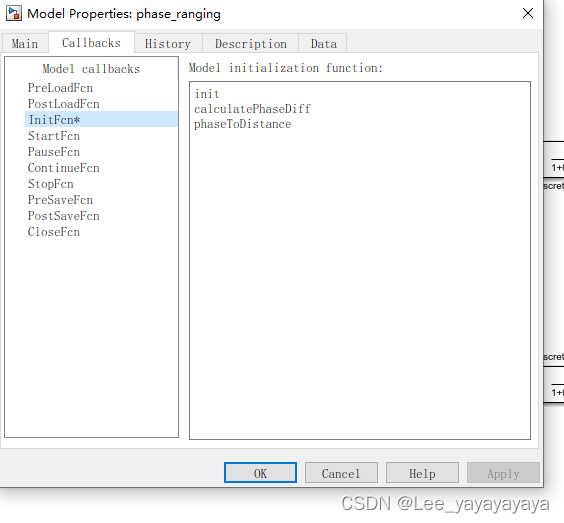
Matlab的Simulink系统仿真(simulink调用m函数)
这几天要用Simulink做一个小东西,所以在网上现学现卖,加油! 起初的入门是看这篇文章MATLAB 之 Simulink 操作基础和系统仿真模型的建立_matlab仿真模型搭建-CSDN博客 写的很不错 后面我想在simulink中调用m文件 在 Simulink 中调用 MATLA…...

C语言中操作符详解(一)
众所周知,在我们的C语言中有着各式各样的操作符,并且在此之前呢,我们已经认识并运用了许许多多的操作符,都是诸君的老朋友了昂 操作符作为我们使用C语言的一个非常非常非常重要的工具,诸君一定要加以重视,…...

【论文阅读】Multi-Camera Unified Pre-Training via 3D Scene Reconstruction
论文链接 代码链接 多摄像头三维感知已成为自动驾驶领域的一个重要研究领域,为基于激光雷达的解决方案提供了一种可行且具有成本效益的替代方案。具有成本效益的解决方案。现有的多摄像头算法主要依赖于单目 2D 预训练。然而,单目 2D 预训练忽略了多摄像…...

深入了解NumPy的原理与使用
文章目录 一、引言二、NumPy的原理1. 多维数组对象2. 广播(Broadcasting)3. 内存效率和速度 三、NumPy的使用1. 创建数组2. 数组操作3. 广播(Broadcasting)示例 四、总结 一、引言 在Python的数据科学和科学计算领域,…...

Linux Centos 环境下搭建RocketMq集群(双主双从)
1、下载rocketmq的包 下载 | RocketMQ 2、配置环境变量 1、编辑环境变量文件:vim /etc/profile2、加入如下配置: #rocketmq 4.9.8 ROCKETMQ_HOME/home/rocketmq/rocketmq-4.9.8 export PATH${ROCKETMQ_HOME}/bin:${PATH}3、刷新配置:source…...

全网最全postman接口测试教程和项目实战~从入门到精通
Postman实现接口测试内容大纲一览: 一、什么是接口?为什么需要接口? 接口指的是实体或者软件提供给外界的一种服务。 因为接口能使我们的实体或者软件的内部数据能够被外部进行修改。从而使得内部和外部实现数据交互。所以需要接口。 比如&…...

【ARM】MDK Debug模式下Disassembly窗口介绍
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 主要了解Disassembly窗口中包含的内容,和如何利用Disassembly中的内容了解程序的存储和调用情况。 2、 问题场景 对于Disassembly窗口中具体包含的内容不了解,无法合理地应用Disassembly窗口…...

灵活的招聘管理系统有五种方法帮助成功招聘
还记得以前的时代吗?这取决于你的年龄,直到智能手机、流媒体电视和电子邮件出现。今天,任何活着的成年人都经历了技术上的巨大变化,这创造了一种新的行为方式。人才获取也是如此。 一个值得推荐的招聘管理系统 招聘团队被困在满足…...

美摄科技匿名化处理解决方案,包含模糊、同色、马赛克、效果遮挡等各种形式
信息安全已成为企业发展中不可忽视的重要一环,随着信息安全法规的日益严格和公众对个人隐私保护意识的不断提高,企业如何在保障业务顺畅进行的同时,满足信息安全和隐私保护的要求,成为了亟待解决的问题。美摄科技凭借其强大的技术…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
