当前位置： 首页 > news >正文

【自动驾驶】通过下位机发送的加速度、角速度计算机器人在世界坐标系中的姿态

news 2026/2/9 12:17:27

文章目录

    • 原始代码
      • 全局变量定义
      • 逆平方根函数
      • 四元数解算函数
      • 理论解释
        • 四元数
        • 加速度计数据归一化
        • 计算方向余弦矩阵的第三行
        • 计算误差
        • 计算并应用积分反馈
        • 应用比例反馈
        • 积分陀螺仪数据，更新四元数
        • 归一化四元数
        • 更新姿态数据
      • 整体流程

原始代码

#define SAMPLING_FREQ 20.0f // 采样频率
/**************************************
Function: 平方根倒数 求四元数用到
***************************************/
float InvSqrt(float number)
{volatile long i;volatile

相关文章：

【自动驾驶】通过下位机发送的加速度、角速度计算机器人在世界坐标系中的姿态

文章目录 原始代码全局变量定义逆平方根函数四元数解算函数理论解释四元数加速度计数据归一化计算方向余弦矩阵的第三行计算误差计算并应用积分反馈应用比例反馈积分陀螺仪数据，更新四元数归一化四元数更新姿态数据整体流程原始代码 #define SAMPLING_FREQ 20.0f // 采样频率…...

编程日记 2024/6/22 2:57:58

Python 设计模式(第2版) -- 第四部分（其他设计模式）

Python 设计模式(第2版) 最后介绍下其他设计模式。 模型—视图—控制器（MVC）-- 复合模式 根据 GoF 的定义，“复合模式将两个或更多模式组合成解决常见或普遍性问题的解决方案”。复合模式不是同时使用的一组模式，而是一个问题的…...

编程日记 2024/6/22 2:54:53

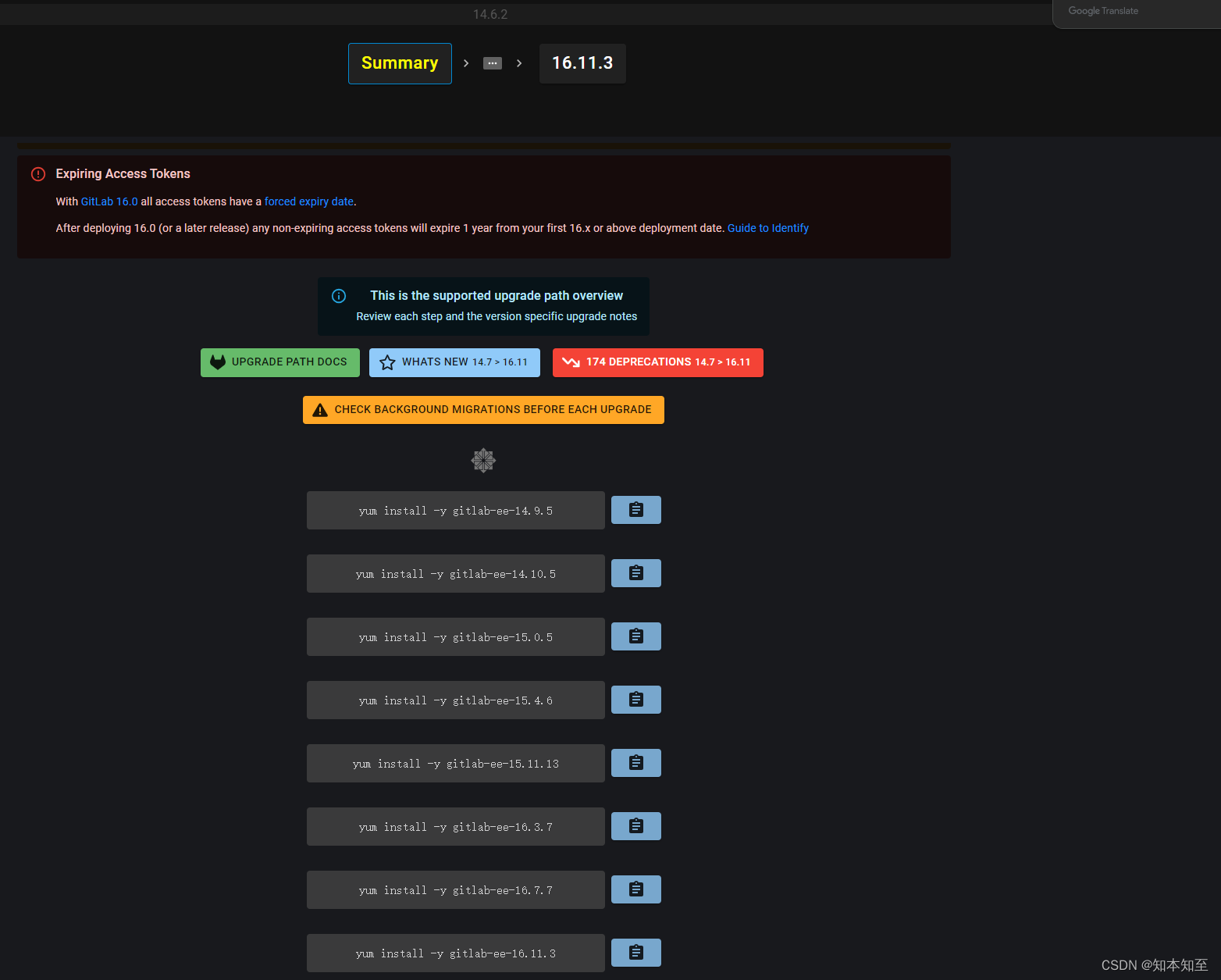
gitlab升级16.11.3-ee

背景 这是事后一段时间补充记录的博客。 升级目的：修补漏洞CVE-2024-4835 未经认证的威胁攻击者能够利用该漏洞在跨站脚本 (XSS) 攻击中，轻松接管受害者账户。 gitlab版本为14.6.2-ee升级至16.11.3-ee 思路 翻阅文档找升级方法及升级版本路径。使用…...

编程日记 2024/6/22 2:53:52

剑指offer 算法题（搜索二维矩阵）

剑指offer 第二题 去力扣里测试算法 思路一&#xff1a; 直接暴力遍历二维数组。 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (unsigned int i{ 0 }; i < matrix.size(); i){for (unsigned int j{ 0 };…...

编程日记 2024/6/22 2:52:51

SaaS平台数据对接为什么要选择API对接？

SaaS平台数据对接是指将一个或多个SaaS平台中的数据集成到其他应用或平台中的过程。在当前的数字化时代&#xff0c;企业越来越倾向于使用SaaS平台来管理他们的业务和数据。然而&#xff0c;这些数据通常散布在不同的SaaS平台中&#xff0c;这对于企业数据的整合和分析来说可能…...

编程日记 2024/6/22 2:51:50

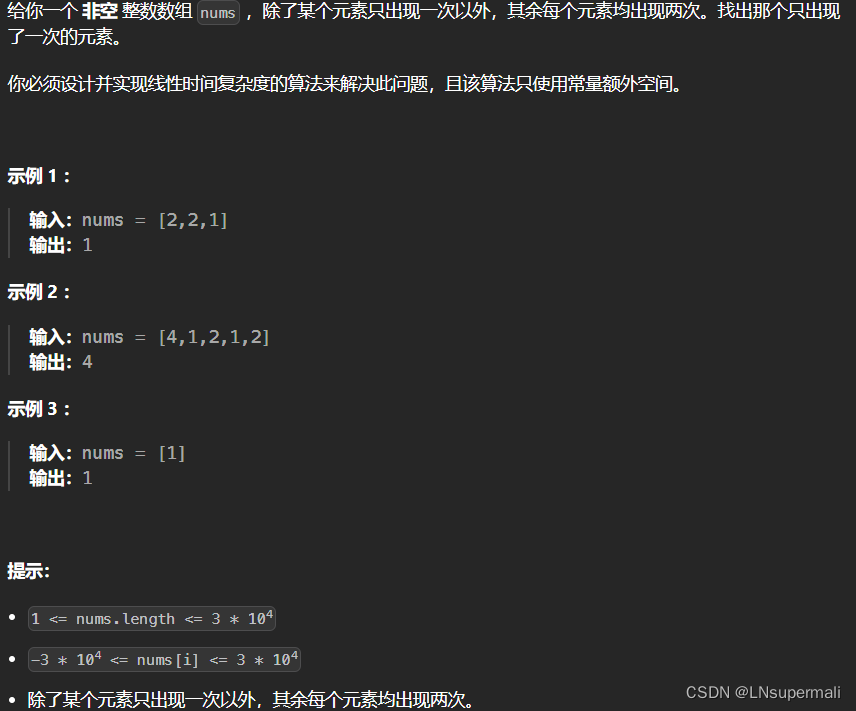
力扣136. 只出现一次的数字

Problem: 136. 只出现一次的数字 文章目录 题目描述思路复杂度Code 题目描述 思路 由于题目要求使用线性时间复杂度和常量级的空间复杂度&#xff0c;再加上找重复元素这个特性&#xff0c;我们可以想到使用位运算来求解&#xff1a; 1.任何数与其本身异或得0&#xff0c;任何…...

编程日记 2024/6/22 2:50:49

重学java 74.Lombok的使用

少点心气&#xff0c;多点干劲 —— 24.6.18 一、lombok的安装使用 1.作用: 简化javabean开发 2.使用: a.下插件 ->如果是idea2022不用下载了,自带 b.导lombok的jar包 安装教程&#xff1a; http://t.csdnimg.cn/wq9MM c.修改设置 二、lombok的介绍 Lombok通过增加一…...

编程日记 2024/6/22 2:47:46

数据结构6---树

一、定义 树(Tree)是n(n>0)个结点的有限集。当n0时成为空树,在任意一棵非空树中: 1、有且仅有一个特定的称为根(Root)的结点; 2、当n>1时,其余结点可分为m(m>日)个互不相交的有限集T1、T2、...、 Tm&#xff0c;其中每一个集合本身又是一棵树&#xff0c;并且称为根的…...

编程日记 2024/6/22 2:46:45

一键制作，打造高质量的数字刊物

随着数字化时代的到来&#xff0c;数字刊物已经成为信息传播的重要载体。它以便捷、环保、互动性强等特点&#xff0c;受到了越来越多人的青睐。然而&#xff0c;如何快速、高效地制作出高质量的数字刊物&#xff0c;成为许多创作者面临的难题。今天&#xff0c;教大家一个制作…...

编程日记 2024/6/22 2:45:43

Java面试题：对比继承Thread类和实现Runnable接口两种创建线程的方法，以及它们的优缺点

Java 中创建线程有两种主要的方法&#xff1a;继承 Thread 类和实现 Runnable 接口。下面我将分别介绍这两种方法&#xff0c;并对比它们的优缺点。 继承 Thread 类 方法&#xff1a; 创建一个继承自 Thread 的子类。重写 Thread 类的 run 方法。创建子类的实例并调用 start…...

编程日记 2024/6/22 2:44:42

编译原理-各章典型题型+思路求解

第2章文法和语言习题 基础知识&#xff1a; 思路&#xff1a; 基础知识&#xff1a; 思路&#xff1a; 基础知识&#xff1a; 编译原理之 短语&直接短语&句柄 定义与区分_编译原理短语,直接短语,句柄-CSDN博客 思路&#xff1a; 题目&#xff1a; 基础解释&#xff1a…...

编程日记 2024/6/22 2:43:41

【绝对有用】C++ vector排序

在 C 中&#xff0c;有多种方法可以对向量&#xff08;即 std::vector&#xff09;进行排序。最常用的方法是使用标准库中的 std::sort 函数。以下是一些例子&#xff1a; 使用 std::sort 函数 std::sort 函数是标准库 <algorithm> 中的一个函数&#xff0c;可以对向量…...

编程日记 2024/6/22 2:42:40

linux——VScode安装

方法一&#xff1a;使用snap一键安装 Snap Store 是 Ubuntu、Debian、Fedora 和其他几个 Linux 发行版中的一个应用商店&#xff0c;提供了数千个应用程序和工具的安装。Snap Store 使用 Snap 包格式&#xff0c;这是一种通用的 Linux 软件包格式&#xff0c;使得在不同的 Lin…...

编程日记 2024/6/22 2:41:39

X-LoRA：高效微调 LoRA 系列，实现不同领域知识专家混合模型

&#x1f4dc; 文献卡 X-LoRA: Mixture of Low-Rank Adapter Experts, a Flexible Framework for Large Language Models with Applications in Protein Mechanics and Molecular Design作者: Eric L. Buehler; Markus J. BuehlerDOI: 10.48550/arXiv.2402.07148摘要:We report…...

编程日记 2024/6/22 2:40:37

基于卷积神经网络的目标检测

卷积神经网络基础知识 1.什么是filter 通常一个6x6的灰度图像&#xff0c;构造一个3*3的矩阵&#xff0c;在卷积神经网络中称之为filter,对&#xff16;x6的图像进行卷积运算。 2.什么是padding 假设输出图像大小为nn与过滤器大小为ff&#xff0c;输出图像大小则为(n−f1)∗(…...

编程日记 2024/6/22 2:39:36

Mysqld数据库管理

一.Mysqld数据库类型 常用的数据类型 int 整型 无符号[0-4294967296&#xff08;2的32次方&#xff09;-1]&#xff0c;有符号[-2147483648&#xff08;2的31次方&#xff09;-2147483647]float单精度浮点 4字节32位double双精度浮点 8字节64位char固定长度的字符类型…...

编程日记 2024/6/22 2:38:35

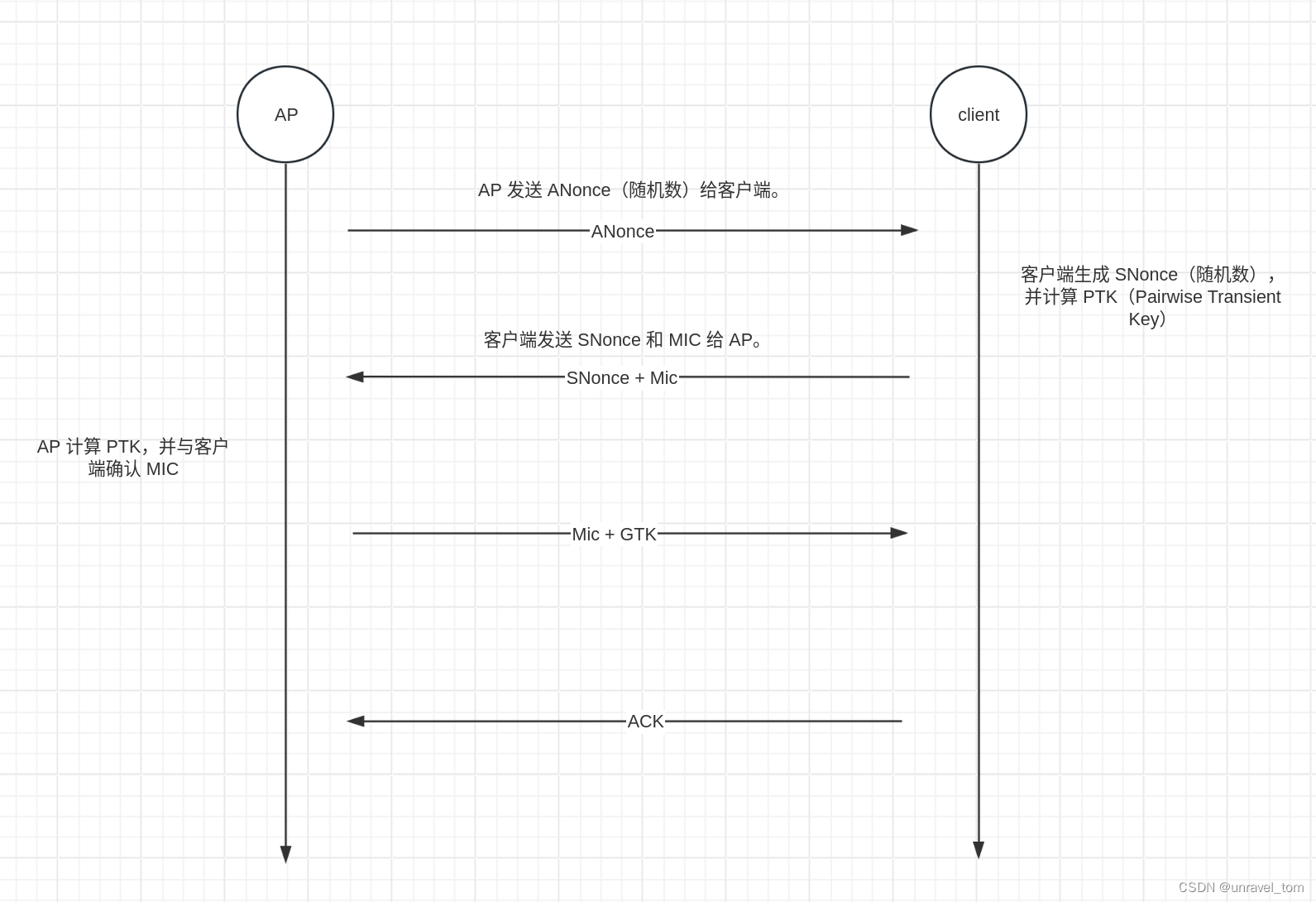
Wifi通信协议：WEP，WPA，WPA2，WPA3，WPS

前言 无线安全性是保护互联网安全的重要因素。连接到安全性低的无线网络可能会带来安全风险&#xff0c;包括数据泄露、账号被盗以及恶意软件的安装。因此&#xff0c;利用合适的Wi-Fi安全措施是非常重要的&#xff0c;了解WEP、WPA、WPA2和WPA3等各种无线加密标准的区别也是至…...

编程日记 2024/6/22 2:37:34

开源【汇总】

开源【汇总】 前言版权推荐开源【汇总】最后 前言 先占个位 2024-6-21 21:29:33 以下内容源自《【创作模板】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此话 本文首次发布于CSDN平台 作者是CSDN日星月云 博客主页是https://jsss-1.blog.csdn.net 禁止其他平台发…...

编程日记 2024/6/22 2:36:32

英文字母表

目录 一 设计原型 二 后台源码 一 设计原型 二 后台源码 namespace 英文字母表 {public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e){foreach (var item in panel1.Controls){if (item ! null)…...

编程日记 2024/6/22 2:35:29

Redis缓存穿透

缓存穿透&#xff1a; 查询一个不存在的数据&#xff0c;mysql查询不到数据也不会直接写入缓存&#xff0c;就会导致每次请求都查数据库。 方法一&#xff1a; 方法二&#xff1a; 布隆过滤器&#xff1a; 简单来说就是一个二进制数组&#xff0c;用0和1来判断数组中是否存在…...

编程日记 2024/6/22 2:33:27

Java - Mysql数据类型对应

Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

编程新知 2025/12/14 11:45:25

什么是库存周转？如何用进销存系统提高库存周转率？

你可能听说过这样一句话&#xff1a; “利润不是赚出来的&#xff0c;是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业&#xff0c;很多企业看着销售不错&#xff0c;账上却没钱、利润也不见了&#xff0c;一翻库存才发现&#xff1a; 一堆卖不动的旧货…...

编程新知 2026/1/26 13:21:10

将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？

Otsu 是一种自动阈值化方法&#xff0c;用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理&#xff0c;能够自动确定一个阈值&#xff0c;将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

编程新知 2026/1/9 19:36:58

高等数学（下）题型笔记（八）空间解析几何与向量代数

目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

编程新知 2026/1/28 9:04:29

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾&#xff1a; 在上一篇中&#xff0c;我们成功地为应用集成了数据库&#xff0c;并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了&#xff01;但是&#xff0c;如果你仔细审视那些 API&#xff0c;会发现它们还很“粗糙”&#xff1a;有…...

编程新知 2026/1/22 20:46:43

零基础设计模式——行为型模式 - 责任链模式

第四部分&#xff1a;行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习&#xff01;行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想&#xff1a;使多个对象都有机会处…...

编程新知 2026/1/31 9:33:18

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角&#xff0c;以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向&#xff0c;距离坐标原点x个像素;第二个是y坐标&#xff0c;表示当前位置为垂直方向&#xff0c;距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32

Linux离线（zip方式）安装docker

目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1&#xff1a;修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本&#xff1a;CentOS 7 64位 内核版本&#xff1a;3.10.0 相关命令&#xff1a; uname -rcat /etc/os-rele…...

编程新知 2025/11/23 23:50:53