机器人里程计(Odometry)
机器人里程计(Odometry)是机器人定位和导航中的一个关键概念,它涉及到利用传感器数据来估计机器人在环境中的位置和姿态。里程计的基本原理是根据机器人自身动作的反馈来计算其相对于初始位置的位移。这通常包括机器人从一个已知位置开始,然后使用各种类型的传感器来测量其自身的运动。
以下是一些常见的里程计类型:
1. **轮式里程计(Wheel Odometry)**:
- 使用安装在机器人轮子上的编码器来测量轮子的转速和转动角度。
- 根据轮子的直径和编码器读数,可以计算出机器人在地面上的位移。
- 这种方法简单且成本低,但受地面摩擦力、打滑和磨损的影响,长时间累积误差较大。
2. **惯性测量单元(IMU)**:
- IMU包含加速度计和陀螺仪,用于测量线性和角加速度。
- 可以结合轮式里程计数据,通过滤波器(如卡尔曼滤波器)来减少累积误差。
3. **视觉里程计(Visual Odometry,VO)**:
- 利用相机捕捉到的连续图像序列,通过特征匹配等计算机视觉技术来估计机器人运动。
- 可分为单目和双目视觉里程计,后者能提供更准确的距离信息。
- 在光照稳定和纹理丰富的环境中效果较好。
4. **激光里程计(Laser Odometry)**:
- 利用激光雷达传感器获取周围环境的点云数据,通过比较连续点云之间的差异来估计机器人位移。
- 需要复杂的点云匹配算法,但精度较高。
5. **多传感器融合**:
- 结合多种传感器的数据,如轮式里程计、IMU、视觉和激光数据,以提高定位精度和鲁棒性。
里程计是许多机器人技术的核心组成部分,比如在SLAM(Simultaneous Localization and Mapping,同时定位与地图构建)算法中,它提供了机器人在未知环境中移动的初步估计,然后通过其他传感器数据(如激光扫描或视觉特征)进行修正和优化,以构建地图并精确定位机器人。
然而,里程计的一个重要缺点是其误差会随时间累积,因此,在长时间或长距离操作中,需要结合其他定位方法(如GPS、信标定位或全局定位系统)来定期校正里程计数据,以维持较高的定位精度。
相关文章:
)
机器人里程计(Odometry)
机器人里程计(Odometry)是机器人定位和导航中的一个关键概念,它涉及到利用传感器数据来估计机器人在环境中的位置和姿态。里程计的基本原理是根据机器人自身动作的反馈来计算其相对于初始位置的位移。这通常包括机器人从一个已知位置开始&…...

后端实现预览pdf,mp4,图片
PDF预览 /*** pdf预览* param response*/RequestMapping(value "/preview")public void showPdf(HttpServletResponse response) {try {//String filePath this.getClass().getClassLoader().getResource("../../static/pdf/readme.pdf").getPath();Stri…...

【C++】数据类型、函数、头文件、断点调试、输入输出、条件与分支、VS项目设置
四、基本概念 这部分和C语言重复的部分就简写速过,因为我之前写过一个C语言的系列,非常详细。C和C这些都是一样的,所以这里不再一遍遍重复码字了。感兴趣的同学可以翻看我之前的C语言系列文章。 1、数据类型 编程的本质就是操作数据。 操…...
)
Spring框架的原理及应用详解(六)
本系列文章简介: 在当今的软件开发世界中,随着应用复杂性的不断增加和技术的快速发展,传统的编程方式已经难以满足快速迭代、高可扩展性和易于维护的需求。为此,开发者们一直在寻求更加高效、灵活且易于管理的开发框架,以帮助他们应对这些挑战。Spring框架就是在这样的背景…...

C++ | Leetcode C++题解之第151题反转字符串中的单词
题目: 题解: class Solution { public:string reverseWords(string s) {int left 0, right s.size() - 1;// 去掉字符串开头的空白字符while (left < right && s[left] ) left;// 去掉字符串末尾的空白字符while (left < right &…...

Leetcode 415. 字符串相加-大数相加
415. 字符串相加 - 力扣(LeetCode) class Solution {/**2024.6.17大数相加,从2个字符串最后一位开始加,如果没遍历到下标0,就一直遍历,减去‘a’得到数值,循环结束条件就是 字符串1遍历完了&am…...
IDEA集成Docker实现快捷部署
本文已收录于专栏 《运维》 目录 背景介绍优势特点操作步骤一、修改Docker配置二、配置Docker插件三、编写Maven插件四、构建Docker镜像五、创建Docker容器 总结提升 背景介绍 在我们手动通过Docker部署项目的时候,都是通过把打包好的jar包放到服务器上并且在服务器…...
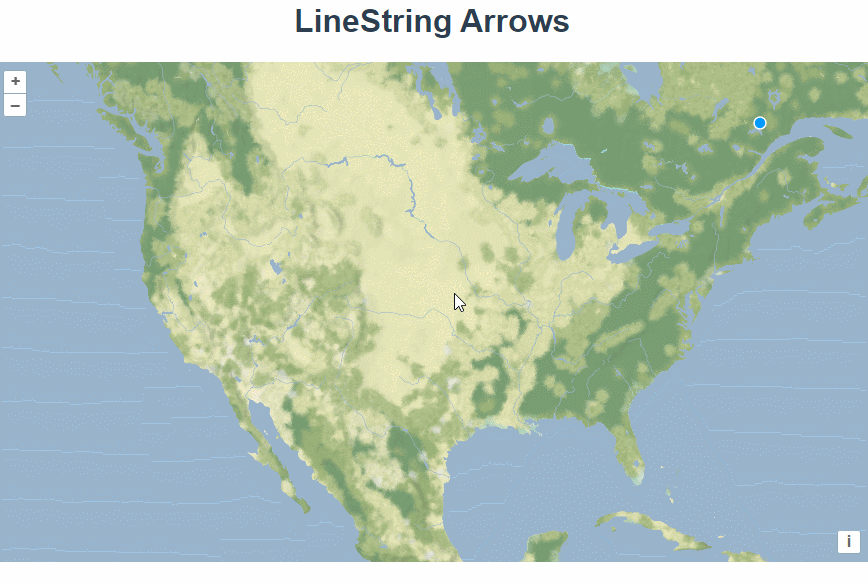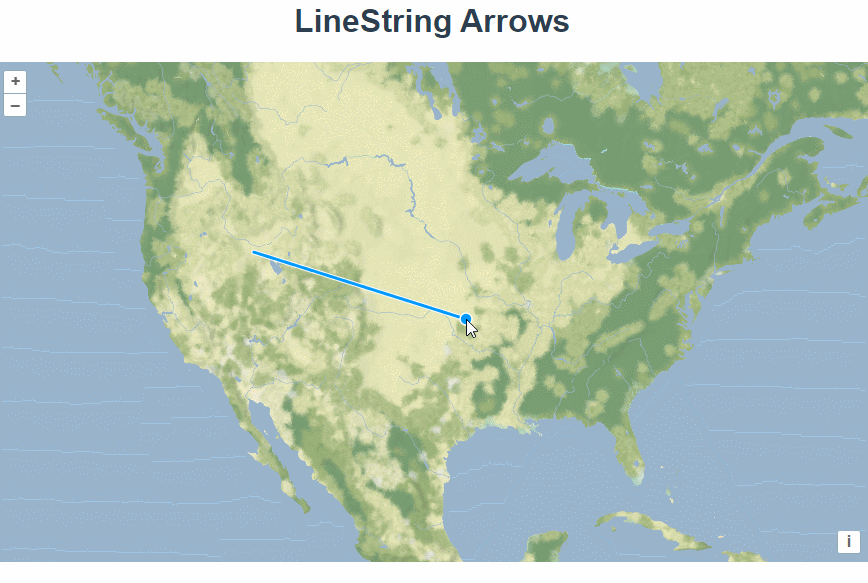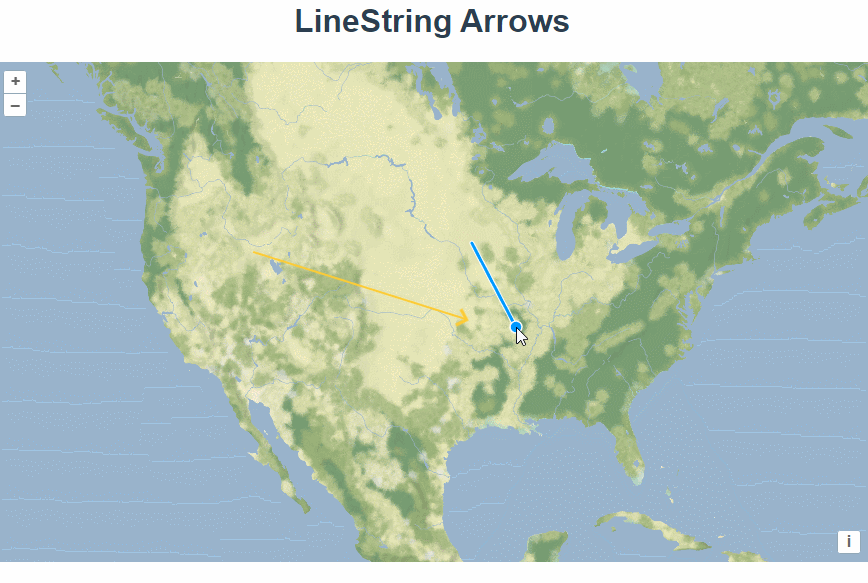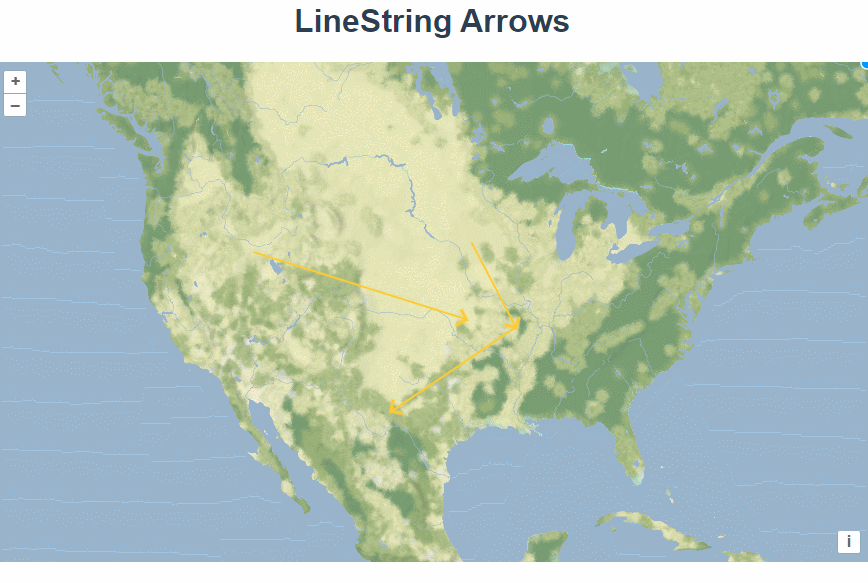
五十四、openlayers官网示例LineString Arrows解析——在地图上绘制箭头
官网demo地址: LineString Arrows 这篇介绍了在地图上绘制箭头。 创建一个矢量数据源,将其绑定为draw的数据源并展示在矢量图层上。 const source new VectorSource();const vector new VectorLayer({source: source,style: styleFunction,});map.ad…...

内核学习——3、自旋锁的作用及其实现
作用: 保护一段临界区的操作时独占的,不能由其他cpu或者线程同时访问破坏数据结构多核系统SMP: 主要考虑一个cpu进入临界区之后,其他CPU不能再去进入这个临界代码区单核系统: 不能被其他进程抢占单核系统自旋锁实现&am…...

恒昌公益第五所“云杉校园”于湖南怀化正式揭牌
在中国近代史上湖南无疑是不可忽视的存在,在“敢为天下先”的湖湘文化熏陶下更是涌现了无数改变国家命运的人物。而作为推动民族复兴与社会进步的关键支柱,重视教育的传统起到的作用功不可没。在迈向中国式现代化的当下,积极推动优质教育资源…...

番外篇 | YOLOv8算法解析和实战应用:车辆检测 + 车辆追踪 + 行驶速度计算
前言:Hello大家好,我是小哥谈。YOLOv8是ultralytics公司在2023年1月10号开源的,是YOLOv5的下一个重大更新版本,目前支持图像分类、物体检测和实例分割任务,在还没有开源时就收到了用户的广泛关注。它是一个SOTA模型,建立在以前YOLO版本的成功基础上,并引入了新的功能和改…...

【React】useState 的原理
useState 是 React Hooks 中的一个核心函数,用于在函数组件中添加和管理状态。以下是 useState 的原理及其工作方式的详细解释: 1. 基本概念 useState 允许你在函数组件中添加 state。它接受一个参数,这个参数是 state 的初始值。useState 返回一个包含两个元素的数组: 第…...

从二元一次方程组到二阶行列式再到克拉默法则
目录 引言1 二元一次方程组什么是二元一次方程组?解法概述示例1. 操作步骤2. 消元法 2 二阶行列式引入行列式行列式定义示例计算 3 克拉默法则什么是克拉默法则?克拉默法则公式使用克拉默法则求解 4 总结 引言 在数学中,线性代数提供了一套强…...
示例:WPF中绑定枚举到ComboBox想显示成中文或自定义名称如何实现
一、目的:在开发过程中绑定的枚举不想显示成英文字段怎么办,这里通过TypeConverter的方式来实现绑定的枚举从定义的特性中读取 二、实现 首先定义如下枚举 [TypeConverter(typeof(DisplayEnumConverter))]public enum MyEnum{[Display(Name "无&q…...

嵌入式系统软件架构设计方法
1.嵌入式系统软件架构设计的目的 嵌入式系统软件架构是开发大型嵌入式系统密集型软件贯穿始终的关键桥梁,同时软件架构也是软件开发的基础。架构设计的目的是: 保证应用的代码逻辑清晰,避免重复的设计;实现软件的可移植性&#…...
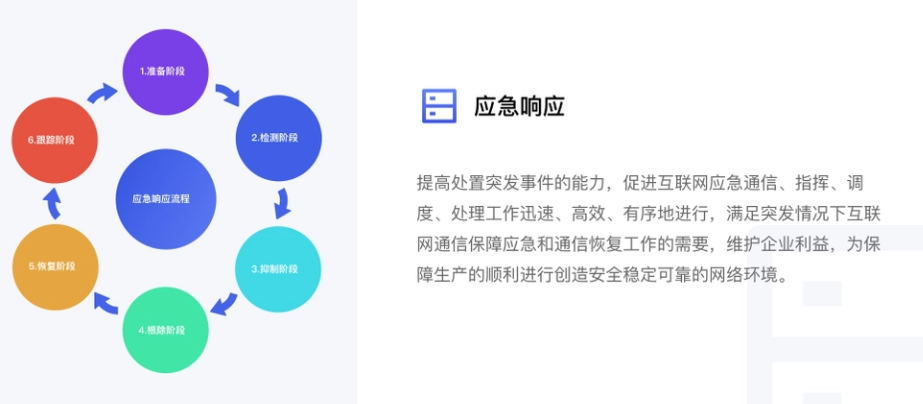
【面试题】风险评估和应急响应的工作流程
风险评估和应急响应是网络安全管理中两个重要的环节。下面分别介绍它们的工作流程: 一、风险评估工作流程: 1.确定评估范围:明确需要评估的信息系统或资产的范围。 2.资产识别:识别并列出所有需要评估的资产,包括硬件…...

Vue70-路由的几个注意点
一、路由组件和一般组件 1-1、一般组件 1-2、路由组件 不用写组件标签。靠路由规则匹配出来,由路由器渲染出来的组件。 1-3、注意点1 一般组件和路由组件,一般放在不同的文件夹,便于管理。 一般组件放在components文件夹下。 1-4、注意点…...
Aidlux 1.4 部署Nextcloud 2024.6实录 没成功
Aidux阉割版Debain10,坑很多,比如找不到实际的系统日志,有知道的大神吗? 1 Apache2安装 # 测试Apache2 sudo apt update && sudo apt upgrade sudo apt install apache2 -y80端口疑似被禁止只能换端口 rootlocalhost:/…...

网络与协议安全复习 - 电子邮件安全
文章目录 PGP(Pretty Good Privacy)功能 S/MIME(Secure/Multipurpose Internet Mail Extensions)DKIM(Domain Keys Identified Mail) PGP(Pretty Good Privacy) 使用符号: Ks:会话密钥、KRa:A 的私钥、KUa:A 的公钥、EPÿ…...

Python里的序列化是什么?
在Python中,序列化(serialization)是一个过程,它可以将数据结构或对象状态转换为可以存储或传输的形式。通常,这意味着将数据结构或对象转换为字节流,以便可以将其写入文件、发送到网络,或用于其…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...
