【代码随想录训练营】【Day38】第九章|动态规划|理论基础|509. 斐波那契数|70. 爬楼梯|746. 使用最小花费爬楼梯
理论基础
动态规划与贪心的区别并不是学习动态规划所必须了解的,所以并不重要。
想要了解动态规划算法题的特点,可以直接做下面三道入门简单题练练手感,找找感觉,很快就能体会到动态规划的解题思想。
总结成一句话就是:动态规划就是利用已知解求未知解,利用之前得到的结果得到下一个结果的过程。
详细的基础理论知识可查阅:《代码随想录》— 动态规划 — 理论基础
斐波那契数
题目详细:LeetCode.509
动态规划入门题,详细的题解可查阅:《代码随想录》— 斐波那契数
Java解法(动态规划):
class Solution {public int fib(int n) {if(n < 2){return n;}int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for(int i = 2; i < n + 1; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}
爬楼梯
题目详细:LeetCode.70
动态规划入门题,思路和解法跟上一题斐波那契数很相似,详细的题解可查阅:《代码随想录》— 爬楼梯
Java解法(动态规划):
class Solution {public int climbStairs(int n) {if(n < 3){return n;}int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for(int i = 3; i < n + 1; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}
使用最小花费爬楼梯
题目详细:LeetCode.746
又是一道简单题,练手非常过瘾,解题思路也十分简单,由题可知:
- 爬楼梯可以从下标为0或1的台阶开始爬楼梯
- 每一次花费后,可选择向上爬一个或者两个台阶
如果那么根据规律,假如我们爬上第三个台阶,会有两种情况:
- 第一种:从下标为0的台阶开始,向上爬两个台阶到达第三个台阶
- 第二种:从下标为1的台阶开始,向上爬一个台阶到达第三个台阶
- 为了使用最小花费爬楼梯,我们爬上第三个台阶的消费应该取两种花费情况中的最小值,即
cost[3] = Math.min(cost[1] + cost[3], cost[2] + cost[3]); - 同理我们可以得到后序各个台阶花费情况,即本题的递推公式为
cost[i] = Math.min(cost[i - 1] + cost[i], cost[i - 2] + cost[i]);
当我们遍历结束后,得到了到达各个台阶的最小花费,但要注意,此时我们到达楼梯顶部的最小花费这一最终返回结果还被没计算出来:
cost[cost.length - 1]的值仅表示到达第cost.length - 1个台阶的最小花费而已cost[cost.length - 2]的值仅表示到达第cost.length - 2个台阶的最小花费而已- 那么当我们到达第
cost[cost.length - 1]或cost[cost.length - 2]个台阶后,也可以选择向上爬一个或者两个台阶 - 所以我们最后还需要通过比较
cost[cost.length - 1]和cost[cost.length - 2],取两者之间的最小值来作为到达楼梯顶部的最小花费
Java解法(动态规划):
class Solution {public int minCostClimbingStairs(int[] cost) {for(int i = 2; i < cost.length; i++){cost[i] = Math.min(cost[i - 1] + cost[i], cost[i - 2] + cost[i]);}return Math.min(cost[cost.length - 1], cost[cost.length - 2]);}
}
相关文章:

【代码随想录训练营】【Day38】第九章|动态规划|理论基础|509. 斐波那契数|70. 爬楼梯|746. 使用最小花费爬楼梯
理论基础 动态规划与贪心的区别并不是学习动态规划所必须了解的,所以并不重要。 想要了解动态规划算法题的特点,可以直接做下面三道入门简单题练练手感,找找感觉,很快就能体会到动态规划的解题思想。 总结成一句话就是…...
| 机考必刷)
华为OD机试题 - 快递货车(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:快递货车题目输入输出示例一输入输出Code解题思路版权说明华为O…...

前端——7.图像标签和路径
这篇文章,我们来讲解一下图像标签 目录 1.图像标签 1.1介绍 1.2实际展示 1.3图像标签的属性 1.3.1 alt属性 1.3.2 title属性 1.3.3 width / height 属性 1.3.4 border属性 1.4注意事项 2.文件夹 2.1目录文件夹和根目录 2.2 VSCode打开目录文件夹 3.路…...

java -- stream流
写在前面: stream流一直在使用,但是感觉还不够精通,现在深入研究一下。 stream这个章节中,会用到 函数式接口–lambda表达式–方法引用的相关知识 介绍 是jdk8引进的新特性。 stream流是类似一条流水线一样的操作,每次对数据进…...

【Spring6】| Bean的四种获取方式(实例化)
目录 一:Bean的实例化方式 1. 通过构造方法实例化 2. 通过简单工厂模式实例化 3. 通过factory-bean实例化 4. 通过FactoryBean接口实例化 5. BeanFactory和FactoryBean的区别(面试题) 6. 使用FactoryBean注入自定义Date 一:…...
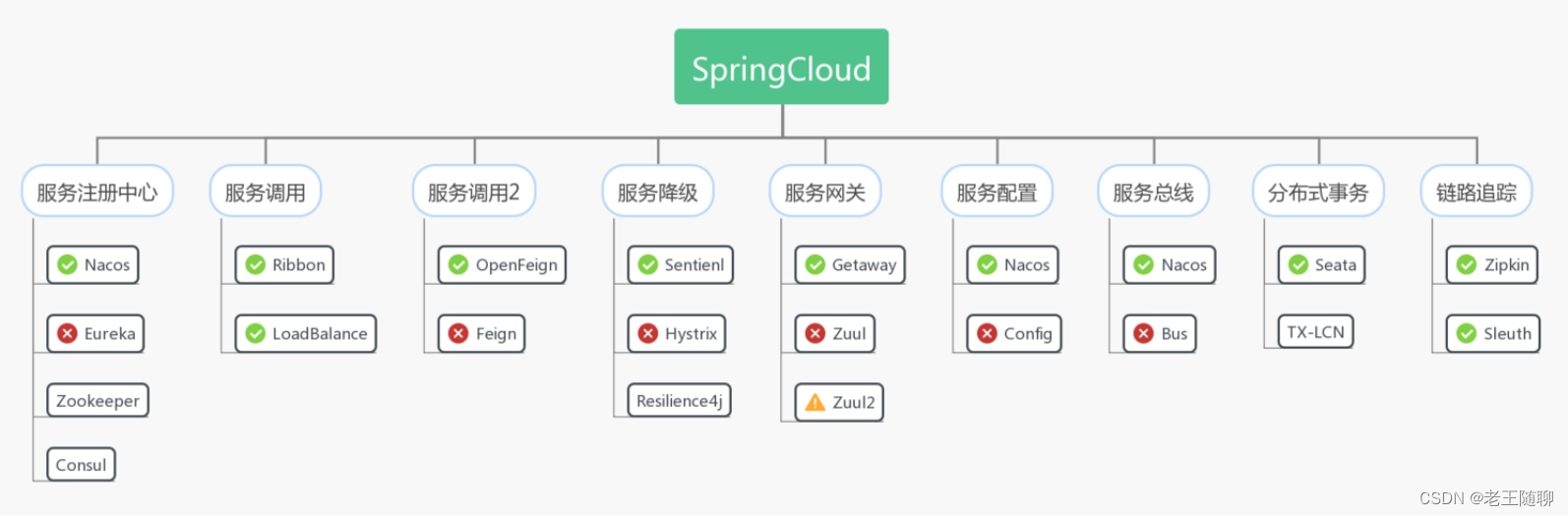
01: 新手学SpringCloud前需知道的5点
目录 第一点: 什么是微服务架构 第二点:为什么需要学习Spring Cloud 第三点: Spring Cloud 是什么 第四点: SpringCloud的优缺点 1、SpringCloud优点 2、SpringCloud缺点 第五点: SpringCloud由什么组成 1&…...

ubuntu apt安装arm交叉编译工具
查找查找编译目标为32位的gcc-arm交叉编译器命令apt-cache search arm|awk index($1,"arm")!0 {print}|grep gcc-arm\|g-arm #或者 apt-cache search arm|awk index($1,"arm")!0 {print}|grep -E gcc-arm|g\\-arm输出如下g-arm-linux-gnueabihf - GNU C co…...

阿里云一面经历
文章目录 ES 查询方式都有哪些?1 基于词项的查询term & terms 查询Fuzzy QueryWildcard Query2 基于全文的查询Match QueryQuery String QueryMatch Phrase Query3 复合查询Bool QueryElasticsearch 删除原理ES 大文章怎么存arthas 常用命令arthas 排查问题过程arthas 工作…...

Java Stream中 用List集合统计 求和 最大值 最小值 平均值
对集合数据的统计,是开发中常用的功能,掌握好Java Stream提供的方法,避免自己写代码统计,可以提高工作效率。 先造点数据: pigs.add(new Pig(1, "猪爸爸", 31, "M", false)); pigs.add(new Pig(…...
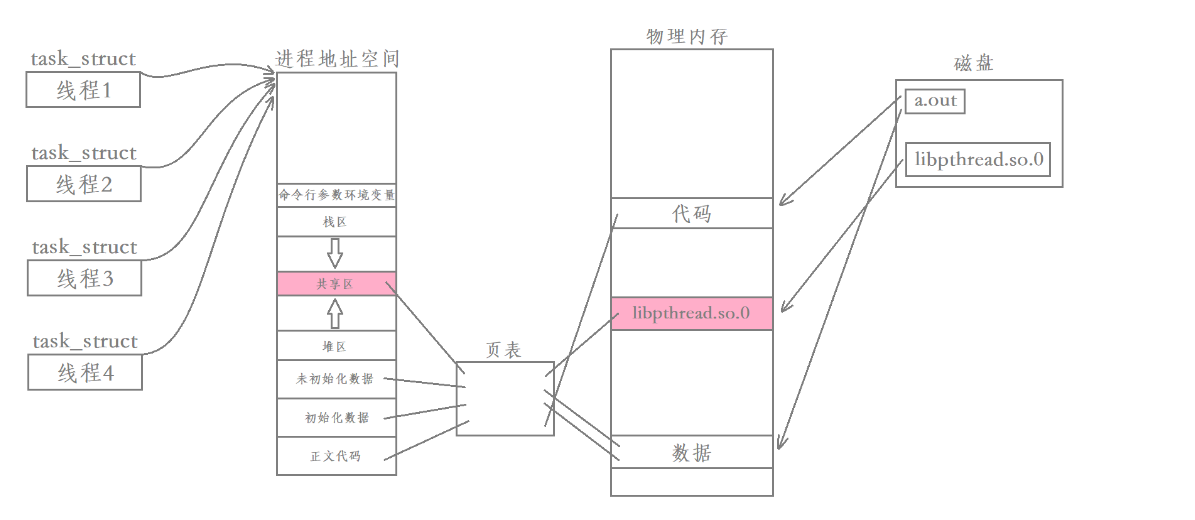
【Linux】多线程---线程控制
进程在前面已经讲过了,所以这次我们来讨论一下多线程。前言:线程的背景进程是Linux中资源及事物管理的基本单位,是系统进行资源分配和调度的一个独立单位。但是实现进程间通信需要借助操作系统中专门的通信机制,但是只这些机制将占…...
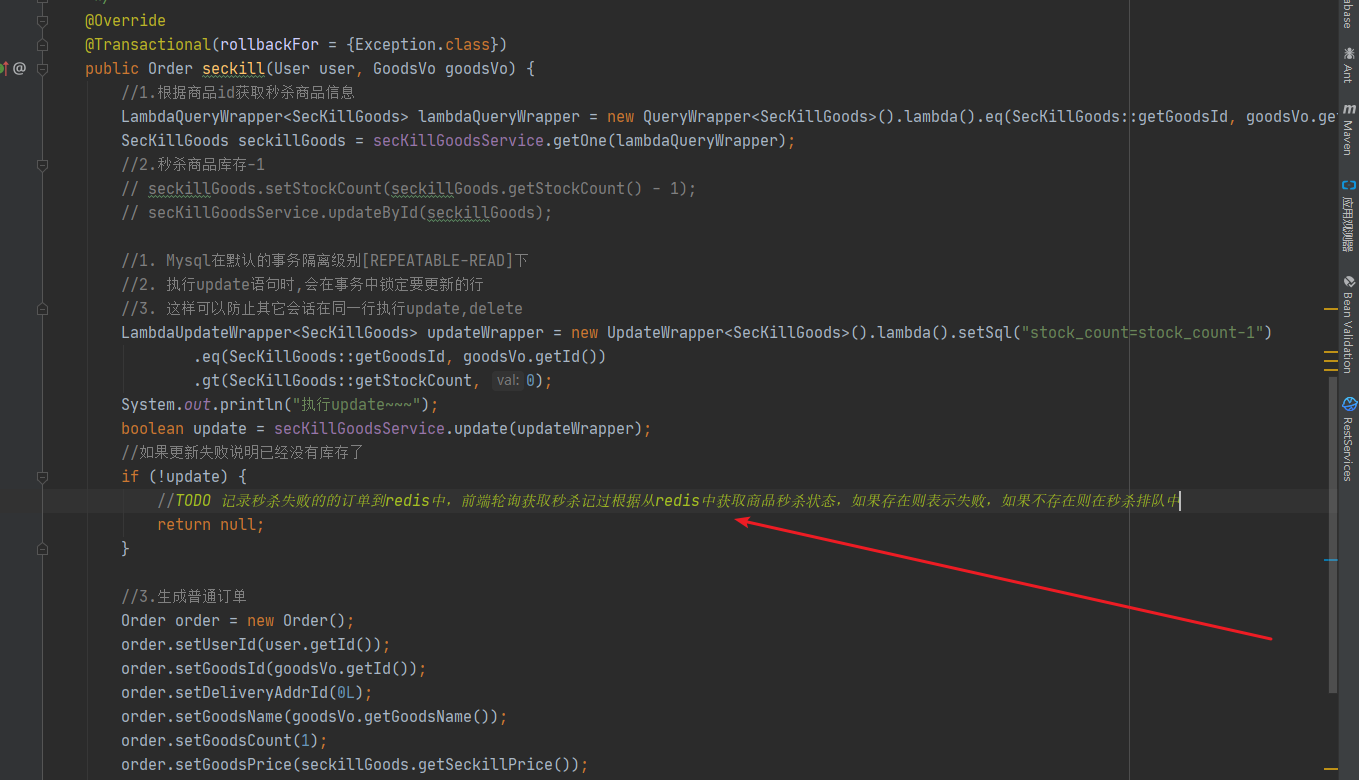
秒杀高并发解决方案
秒杀高并发解决方案 1.秒杀/高并发方案-介绍 秒杀/高并发 其实主要解决两个问题,一个是并发读,一个是并发写并发读的核心优化理念是尽量减少用户到 DB 来"读"数据,或者让他们读更少的数据, 并 发写的处理原则也一样针对秒杀系统需…...

【每日一题】蓝桥杯加练 | Day07
文章目录一、三角回文数1、问题描述2、解题思路3、AC代码一、三角回文数 原题链接:三角回文数 1、问题描述 对于正整数 n, 如果存在正整数 k 使得n123⋯k k(k1)2\frac{k(k1)}{2}2k(k1) , 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066123⋯363 。 如果一…...

条件语句(分支语句)——“Python”
各位CSDN的uu们你们好呀,最近总是感觉特别特别忙,但是却又不知道到底干了些什么,好像啥也没有做,还忙得莫名其妙,言归正传,今天,小雅兰的内容还是Python呀,介绍一些顺序结构的知识点…...

论文投稿指南——中文核心期刊推荐(国家财政)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
面向数据安全共享的联邦学习研究综述
开放隐私计算 摘 要:跨部门、跨地域、跨系统间的数据共享是充分发挥分布式数据价值的有效途径,但是现阶段日益严峻的数据安全威胁和严格的法律法规对数据共享造成了诸多挑战。联邦学习可以联合多个用户在不传输本地数据的情况下协同训练机器学习模型&am…...
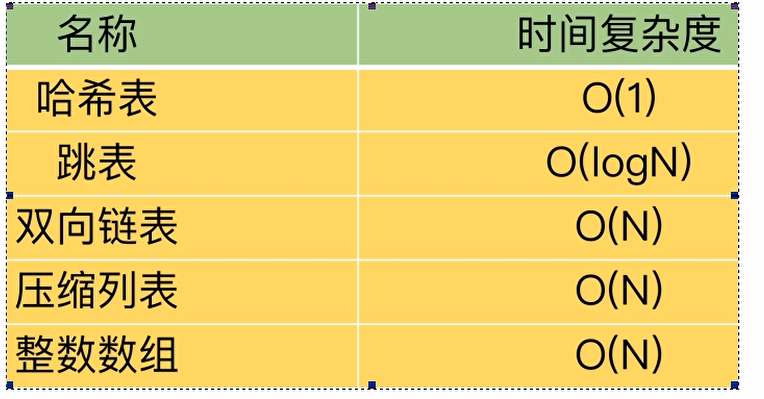
Redis经典五种数据类型底层实现原理解析
目录总纲redis的k,v键值对新的三大类型五种经典数据类型redisObject结构图示结构讲解数据类型与数据结构关系图示string数据类型三大编码格式SDS详解代码结构为什么要重新设计源码解析三大编码格式hash数据类型ziplist和hashtable编码格式ziplist详解结构剖析ziplist的优势(为什…...

Jackson 返回前端的 Response结果字段大小问题
目录 1、问题产生的背景 2、出现的现象 3、解决方案 4、成果展现 5、总结 6、参考文章 1、问题产生的背景 因为本人最近工作相关的对接外部项目,在我们国内有很多程序员都是使用汉语拼音或者部分字母加上英文复合体定义返回实体VO,这样为了能够符合…...

每天五分钟机器学习:你理解贝叶斯公式吗?
本文重点 贝叶斯算法是机器学习算法中非常经典的算法,也是非常古老的一个算法,但是它至今仍然发挥着重大的作用,本节课程及其以后的专栏将会对贝叶斯算法来做一个简单的介绍。 贝叶斯公式 贝叶斯公式是由联合概率推导而来 其中p(Y|X)称为后验概率,P(Y)称为先验概率…...

C++的入门
C的关键字 C总计63个关键字,C语言32个关键字 命名空间 我们C的就是建立在C语言之上,但是是高于C语言的,将C语言的不足都弥补上了,而命名空间就是为了弥补C语言的不足。 看一下这个例子。在C语言中会报错 #include<stdio.h>…...

数据的存储
类型的意义:使用这个类型开辟内存空间的大小(大小决定了使用范围)如何看待内存空间视角类型的基本归类整型家族浮点数家族构造类型指针类型空类型整型存储解构:整型在计算机中占用四个字节,整型分为无符号整型和有符号整型在计算机…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
