[C++][数据结构][跳表]详细讲解
目录
- 0.什么是跳表?
- 1.SkipList的优化思路
- 2.SkipList的效率如何保证?
- 3.SkipList实现
- 4.SkipList VS 平衡搜索树 && Hash
0.什么是跳表?
- SkipList本质上也是一种查找结构,用于解决算法中的查找问题,跟平衡搜索树和哈希表的价值是一样的,可以作为key或者key/value的查找模型
- SkipList,是在有序链表的基础上发展起来的
- 如果是一个有序的链表,查找数据的时间复杂度是 O ( N ) O(N) O(N)
1.SkipList的优化思路
-
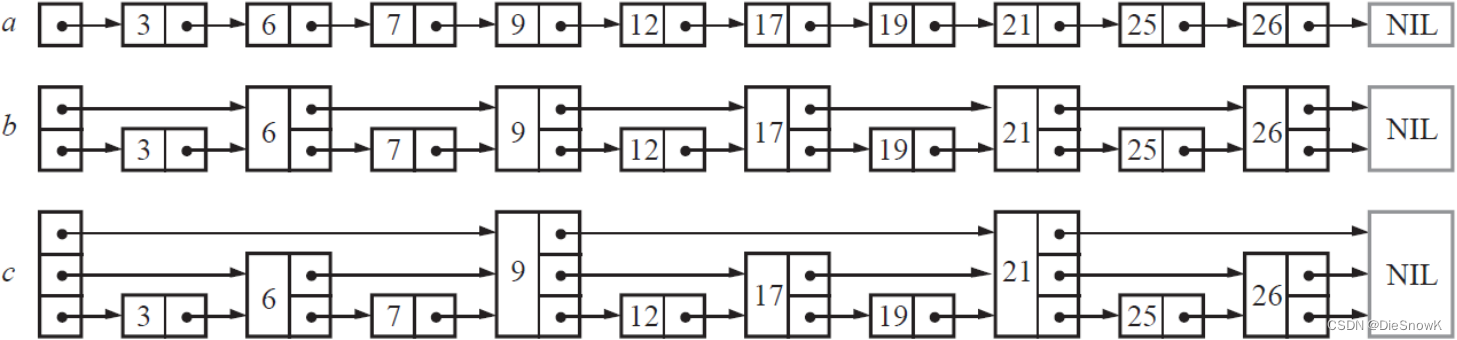
假如每相邻两个节点升高一层,增加一个指针,让指针指向下下个节点,如下图b所示
- 这样所有新增加的指针连成了一个新的链表,但它包含的节点个数只有原来的一半
- 由于新增加的指针,我们不再需要与链表中每个节点逐个进行比较了,需要比较的节点数大概只有原来的一半
-
以此类推,可以在第二层新产生的链表上,继续为每相邻的两个节点升高一层,增加一个指针,从而产生第三层链表,这样搜索效率就进一步提高了,如下图c
-
SkipList正是受这种多层链表的想法的启发而设计出来的
-
实际上,按照上面生成链表的方式,上面每一层链表的节点个数,是下面一层的节点个数的一半,这样查找过程就非常类似二分查找,使得查找的时间复杂度可以降低到 O ( l o g 2 N ) O(log_2N) O(log2N)
-
但是这个结构在插入删除数据的时候有很大的问题
-
插入或者删除一个节点之后,就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系
-
如果要维持这种对应关系,就必须把新插入的节点后面的所有节点(也包括新插入的节点)重新进行调整,这会让时间复杂度重新蜕化成O(n)
-
-
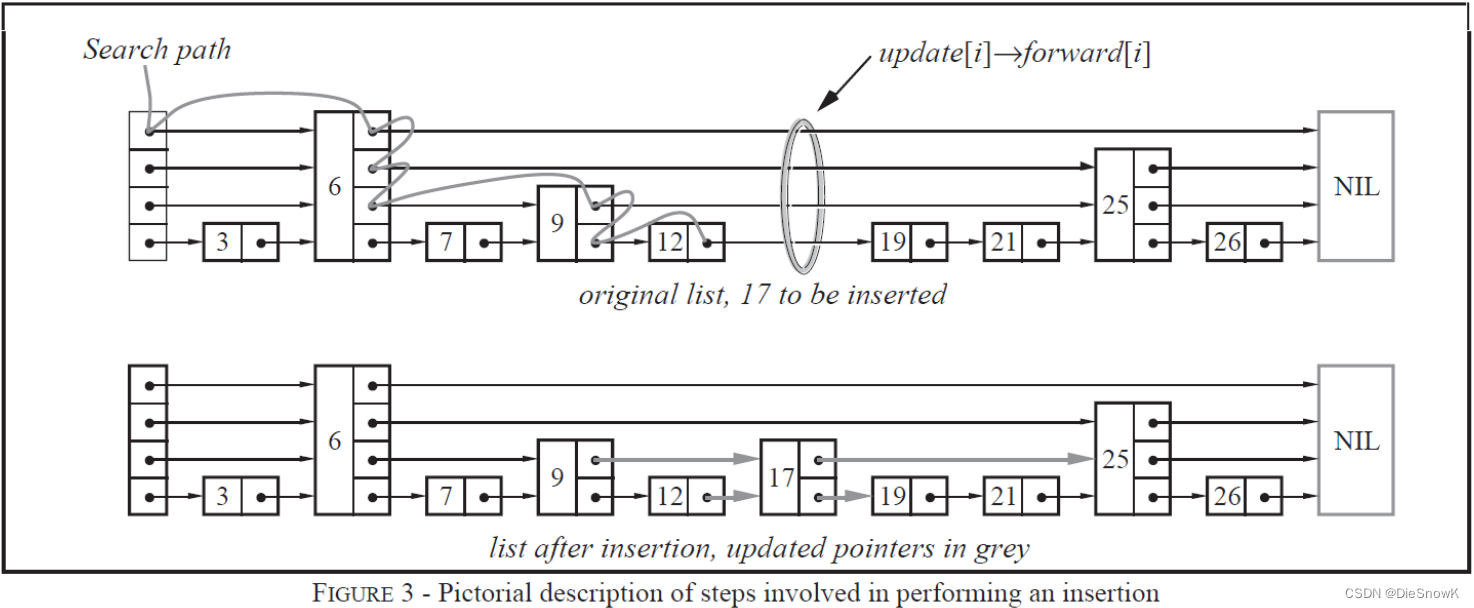
SkipList的设计为了避免这种问题,做了一个大胆的处理
-
不再严格要求对应比例关系,而是插入一个节点的时候随机出一个层数
-
这样每次插入和删除都不需要考虑其他节点的层数, 这样就好处理多了
-
2.SkipList的效率如何保证?
-
SkipList插入一个节点时随机出一个层数,听起来这么随意,如何保证搜索时的效率呢?
-
首先要细节分析的是这个随机层数是怎么来的
- 一般跳表会设计一个最大层数maxLevel的限制
- 其次会设置一个多增加一层的概率p
- 计算这个随机层数的伪代码如下图:

-
**参考:**在Redis的SkipList实现中,这两个参数的取值为:
p = 1/4; maxLevel = 32; -
根据前面
randomLevel()的伪代码,产生越高的节点层数,概率越低- 节点层数至少为1,而大于1的节点层数,满足一个概率分布
- 节点层数恰好等于1的概率为 1 − p 1-p 1−p
- 节点层数大于等于2的概率为 p p p,而节点层数恰好等于2的概率为 p ∗ ( 1 − p ) p*(1-p) p∗(1−p)
- 节点层数大于等于3的概率为 p 2 p^2 p2,而节点层数恰好等于3的概率为 p 2 ∗ ( 1 − p ) p^2*(1-p) p2∗(1−p)
- 节点层数大于等于4的概率为 p 3 p^3 p3,而节点层数恰好等于4的概率为 p 3 ∗ ( 1 − p ) p^3*(1-p) p3∗(1−p)
-
因此,一个节点的平均层数(即包含的平均指针数目),计算如下:
- 当 p = 1 / 2 p=1/2 p=1/2时,每个节点所包含的平均指针数目为2
- 当 p = 1 / 4 p=1/4 p=1/4时,每个节点所包含的平均指针数目为1.33
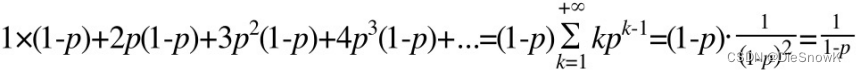
-
SkipList的平均时间复杂度为: O ( l o g N ) O(logN) O(logN),
3.SkipList实现
- 插入结点的关键是找到这个位置的每一层前一个结点
- 比它小,向下走
- 比它大,向右走
struct SkipListNode
{int _val;vector<SkipListNode*> _nextV;SkipListNode(int val, int level): _val(val), _nextV(level, nullptr){}
};class Skiplist
{typedef SkipListNode Node;
public:Skiplist(){srand(time(nullptr));_head = new Node(-1, 1); // 头节点,层数是1}bool Search(int target){Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){if (cur->_nextV[level] && target > cur->_nextV[level]->_val){// 目标值比下一个结点值大,向右走cur = cur->_nextV[level];}else if (!cur->_nextV[level] || target < cur->_nextV[level]->_val){// 下一个结点是空(尾) || 目标值比下一个节点值要小,向下走level--;}else{return true;}}return false;}void Add(int num){vector<Node*> preV = FindPrevNode(num);int n = RandomLevel();Node* newnode = new Node(num, n);// 如果n超过当前最大的层数,那就升高一下_head的层数if (n > _head->_nextV.size()){_head->_nextV.resize(n, nullptr);preV.resize(n, _head);}// 链接前后结点for (size_t i = 0; i < n; i++){newnode->_nextV[i] = preV[i]->_nextV[i];preV[i]->_nextV[i] = newnode;}}bool Erase(int num){vector<Node*> preV = FindPrevNode(num);// 第一层下一个不是val,则val不在表中if (!preV[0]->_nextV[0] || preV[0]->_nextV[0]->_val != num){return false;}Node* del = preV[0]->_nextV[0];// del结点每一层前后指针链接起来for (size_t i = 0; i < del->_nextV.size(); i++){preV[i]->_nextV[i] = del->_nextV[i];}delete del;// 如果删除最高层结点,把头节点的层数也降一下// 可以稍微提高查找效率int i = _head->_nextV.size() - 1;while (i >= 0){if (!_head->_nextV[i]){i--;}else{break;}}_head->_nextV.resize(i + 1);return true;}// SkipList精髓vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;// 插入位置每一层前一个结点指针vector<Node*> preV(level + 1, _head);while (level >= 0){if (cur->_nextV[level] && num > cur->_nextV[level]->_val){// 目标值比下一个结点值大,向右走cur = cur->_nextV[level];}else if (!cur->_nextV[level] || num <= cur->_nextV[level]->_val){preV[level--] = cur;}}return preV;}// v1.0 Cint RandomLevel(){size_t level = 1;// rand() / RAND_MAX -> [0, 1]while (rand() <= RAND_MAX * _p && level <= _maxLevel){level++;}return level;}// v2.0 C++// int RandomLevel()// {// static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());// static std::uniform_real_distribution<double> distribution(0.0, 1.0);// size_t level = 1;// while (distribution(generator) <= _p && level < _maxLevel)// {// ++level;// }// return level;// }
private:Node* _head;size_t _maxLevel = 32;double _p = 0.5;
};
4.SkipList VS 平衡搜索树 && Hash
- SkipList相比平衡搜索树(AVL树和红黑树),都可以做到遍历数据有序,时间复杂度也差不多
- SkipList的优势:
- SkipList实现简单,容易控制
- 平衡树增删查改遍历都更复杂
- SkipList的额外空间消耗更低
- 平衡树节点存储每个值有三叉链,平衡因子/颜色等消耗
- SkipList中 p = 1 / 2 p=1/2 p=1/2时,每个节点所包含的平均指针数目为2
- SkipList中 p = 1 / 4 p=1/4 p=1/4时,每个节点所包含的平均指针数目为1.33
- SkipList实现简单,容易控制
- SkipList的优势:
- SkipList相比哈希表而言,就没有那么大的优势了
- SkipList劣势:
- 哈希表平均时间复杂度是 O(1),比SkipList快
- 哈希表空间消耗略多一点
- SkipList优势:
- 遍历数据有序
- SkipList空间消耗略小一点,哈希表存在链接指针和表空间消耗
- 哈希表扩容有性能损耗
- 哈希表在极端场景下哈希冲突高,效率下降厉害,需要红黑树补足接力
- SkipList劣势:
相关文章:
[C++][数据结构][跳表]详细讲解
目录 0.什么是跳表?1.SkipList的优化思路2.SkipList的效率如何保证?3.SkipList实现4.SkipList VS 平衡搜索树 && Hash 0.什么是跳表? SkipList本质上也是一种查找结构,用于解决算法中的查找问题,跟平衡搜索树…...

tinyxml
github下载相关的软件包,其中有四个文件需要主要需要关注就是分别是tinyxml12.cpp,tinyxml12.h,rss网页xml文件,还有就是官方给的test文件tinyxmltest.cpp。 example1就是提供一个打开文件的方式 int example_1() {XMLDocument …...
Docker(三)-Docker常用命令
1.run run命令执行流程:2.帮助启动类命令 2.1 启动docker systemctl start docker2.2 停止docker systemctl stop docker2.3 重启docker systemctl restart docker2.4查看docker状态 systemctl status docker2.5开机启动 systemctl enable docker2.6查看docker概要信息 …...
[MRCTF2020]PixelShooter
一个apk文件 jeb打开发现是apk文件 apk游戏逆向必须知道的知识: 一般关键数据在 Assets/bin/data/managed/assembly-csharp.dll这个文件里面 我不知道jeb为什么这里我没有 apk是个压缩包 直接解压 这个文件解压也可以发现flag {Unity_1S_Fun_233}...

vue实现的商品列表网页
一、商品列表效果如下 二、代码; vue实现的商品列表网页 , 图片在vue项目的Public文件夹里的 imgs中 <template><div class"common-layout"><!-- el-container:外层容器。 当子元素中包含 <el-header> 或 <el-foo…...

【泛微系统】e-cology非标配功能概览
关于泛微非标功能的功能编号、功能名称及支持版本 编号名称支持版本001考勤功能4.500.0124-9.00+KB900190206002短信通用接口5.000.0327+KB50001003 及以上版本004计划任务接口5.0+KB50001003及以上版本005集成登录接口6.0及以上版本006流程中自定义浏览框5.0+KB50001003及以上…...

Python基础教程(二十八):pip模块
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 💝Ὁ…...

通信系统概述
1.定义 通信系统(也称为通信网络)是利用各种通信线路将地理上分散的、具有独立功能的计算机系统和通信设备按不同的形式连接起来,依靠网络软件及通信协议实现资源共享和信息传递的系统。 2.概述 随着通信技术和网络技术的不断发展ÿ…...
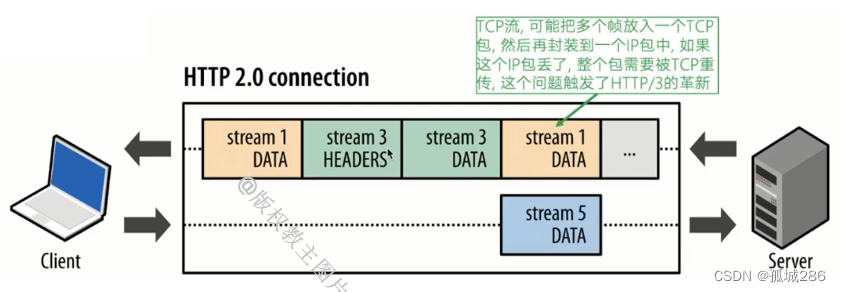
http发展史(http0.9、http1.0、http1.1、http/2、http/3)详解
文章目录 HTTP/0.9HTTP/1.0HTTP/1.1队头阻塞(Head-of-Line Blocking)1. TCP 层的队头阻塞2. HTTP/1.1 的队头阻塞 HTTP/2HTTP/3 HTTP/0.9 发布时间:1991年 特点: 只支持 GET 方法没有 HTTP 头部响应中只有 HTML 内容࿰…...
)
Hadoop 面试题(四)
1. 简述Hadoop节点的动态上线下线的大概操作 ? 在Hadoop集群中,节点的动态上下线指的是在不停止整个集群服务的情况下,添加或移除节点。这种能力对于维护和扩展集群非常重要。以下是Hadoop节点动态上线下线的大概操作步骤: 动态…...

绽放光彩的小程序 UI 风格
绽放光彩的小程序 UI 风格...
电脑文件夹怎么加密?文件夹加密的5种方法
在数字化时代,信息安全显得尤为重要。对于个人电脑用户来说,文件夹加密是一种有效保护隐私和数据安全的方法。本文将介绍五种文件夹加密的方法,帮助您更好地保护自己的重要文件。 如何设置文件夹密码方法一:利用Windows系统自带的…...

异步复位同步释放
目录 描述 输入描述: 输出描述: 参考代码 描述 题目描述: 请使用异步复位同步释放来将输入数据a存储到寄存器中,并画图说明异步复位同步释放的机制原理 信号示意图: clk为时钟 rst_n为低电平复位 d信号输入…...

JupyterLab使用指南(七):JupyterLab使用 LaTeX 生成数学公式
在 JupyterLab 中,可以使用 LaTeX 语法生成复杂的数学公式。JupyterLab 内置对 LaTeX 的支持,使得我们可以方便地在 notebook 中编写和展示数学公式。以下是详细的步骤和示例。 1. 使用 LaTeX 生成数学公式 LaTeX 是一种专门用于排版数学公式的语言。J…...
docker 环境部署
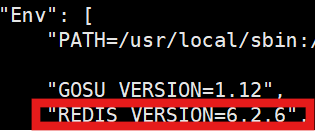
1.Redis部署 用docker拉取redis镜像 docker pull redis 用docker查看拉取的镜像版本号,这里查到的是 6.2.6 版本 docker inspect redis 通过wget指令下载对应版本的tar包,下载完成后解压 wget https://download.redis.io/releases/redis-6.2.6.tar.gz …...

Spring中的ContextPath总结
Spring中的ContextPath总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. ContextPath的概念 在Spring中,ContextPath是指Web应用程序的上下文…...

C++设计模式——Composite组合模式
一,组合模式简介 真实世界中,像企业组织、文档、图形软件界面等案例,它们在结构上都是分层次的。将系统分层次的方式使得统一管理和添加不同子模块变得容易,在软件开发中,组合模式的设计思想和它们类似。 组合模式是…...

Android提供的LruCache类简介(1)
* If your cached values hold resources that need to be explicitly released, * override {link #entryRemoved}. * 如果你cache的某个值需要明确释放,重写entryRemoved() * If a cache miss should be computed on demand for the corresponding keys, * ov…...

【分布式系列】分布式锁timeout了怎么办?
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
方法总结)
System.getProperty()方法总结
System.getProperty()方法总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!System.getProperty()方法是Java中用于获取系统属性的方法之一。它允许我们访问J…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
