洛谷——P2824 排序
题目来源:[HEOI2016/TJOI2016] 排序 - 洛谷![]() https://www.luogu.com.cn/problem/P2824
https://www.luogu.com.cn/problem/P2824
问题思路
本文介绍一种二分答案的做法,时间复杂度为:(n+m)*log(n)*log(n).本题存在nlog(n)的做法,然而其做法没有二分答案的做法通俗易懂.
默认读者已读过原题,故直接介绍思路.
- 二分枚举答案为mid,对于原序列中大于或等于mid的元素,将其转化为1,对于其他元素,将其转化为0.
- 现在,原排列已转化为01序列,m次操作对01序列进行排序.
- 经过m次排序操作后,如果第p个位置上的元素为1,那么更新二分边界 r = mid.否则如果第p个位置上的元素为0,那么更新二分边界 l = mid.
- 如何维护m次操作呢?该问题转化为线段树的修改+查找问题。没有接触过线段树修查问题的读者,建议先去学习相关知识,此处不多赘述.
好了,思路介绍完了,你可能惊讶于为什么二分答案可行.如下便是二分答案可行性的一些解释.
假如经过m次操作后,第p个位置上的元素为x0。我们考虑m次普通的序列排序,但是此次排序咱们让每一个元素都夹带“私货”.对应于问题思路中的第一步,令mid = x0,对于x>=mid的元素,让它带上额外的元素1.对于x<x0的元素,让它带上额外的元素0.经过m次操作后,元素x0位于第p个位置上,且额外的“私货”——元素1,也随之到达了第p个位置.
看到这里是否嗅到了二分答案的味道?既然 mid = x0可行,那么按照mid = x0 - 1,x0 - 2....的要求,给元素分配额外“私货”0和1,那么 1 依旧会随着元素x0来到第p个位置上.然而,假如mid>x0,那么跟随元素x0到达第p个位置上的额外“私货”便是元素0了.
经过上述解释,你应该理解了二分答案在该题目中的可行性.
当我们不再考虑普通的序列排序,而是考虑01序列的排序时,对元素0和1进行排序后的结果,必定能够映射到其普通序列的正确的排序结果上.举个例子,对序列 perm = [1,5,2,4,3] 进行排序,先二分答案 mid = 3,那么perm 转化 01序列 bperm = [0,1,0,1,1],那么对 bperm进行升序排序的结果为: bperm = [0,0,1,1,1],该排序结果能够映射到其普通序列的正确排序结果上,即
==> perm = [1,2,3,4,5].
OK,解释到此结束,更多细节问题请参考代码:
#include<bits/stdc++.h>
using namespace std;const int N = 100005;
int a[N];int ls(int u) { return u << 1; }
int rs(int u) { return u << 1 | 1; }struct tree {int l, r, s, tag;
}tr[N * 4];void build(int u, int l, int r) {tr[u] = { l,r,0,-1 };if (l == r)return;int mid = l + r >> 1;build(ls(u), l, mid);build(rs(u), mid + 1, r);
}void addTag(int u, int v) {tr[u].s = v * (tr[u].r - tr[u].l + 1);tr[u].tag = v;
}void pu(int u) {tr[u].s = tr[ls(u)].s + tr[rs(u)].s;
}void pd(int u) {// tag == -1代表该线段的标签已重置...if (tr[u].tag != -1) {addTag(ls(u), tr[u].tag);addTag(rs(u), tr[u].tag);tr[u].tag = -1;}
}void update(int L, int R, int u, int v) {if (tr[u].l > R || tr[u].r < L) return;if (L <= tr[u].l && tr[u].r <= R) {addTag(u, v);return;}pd(u);int mid = (tr[u].l + tr[u].r) >> 1;if (L <= mid) update(L, R, ls(u), v);if (R > mid) update(L, R, rs(u), v);pu(u);
}int query(int L, int R, int u) {if (tr[u].l > R || tr[u].r < L) return 0;if (L <= tr[u].l && tr[u].r <= R) return tr[u].s;pd(u);int mid = (tr[u].l + tr[u].r) >> 1;int ans = 0;if (L <= mid) ans = query(L, R, ls(u));if (R > mid) ans = ans + query(L, R, rs(u));return ans;
}int main() {ios::sync_with_stdio(0), cin.tie(0);int n, m;cin >> n >> m;for (int i = 1;i <= n;i++) cin >> a[i];vector<array<int, 3>>op(m);for (int i = 0;i < m;i++) {cin >> op[i][0] >> op[i][1] >> op[i][2];}build(1, 1, n);int q;cin >> q;int l = 0, r = n + 1;while (l + 1 != r) {update(1, n, 1, 0);int mid = l + r >> 1;for (int i = 1;i <= n;i++)if (a[i] >= mid) update(i, i, 1, 1);for (int i = 0;i < m;i++) {int o = op[i][0], ql = op[i][1], qr = op[i][2];int k = query(ql, qr, 1);int cnt = qr - ql + 1;// [qr-k+1,qr]全为1,[ql,qr-k]全为0...if (k == 0 || k == cnt) continue;if (o == 0) {update(ql, qr - k, 1, 0);update(qr - k + 1, qr, 1, 1);}else {update(ql, ql + k - 1, 1, 1);update(ql + k, qr, 1, 0);}}query(q, q, 1) == 1 ? l = mid : r = mid;}cout << l << '\n';return 0;
}相关文章:
洛谷——P2824 排序
题目来源:[HEOI2016/TJOI2016] 排序 - 洛谷https://www.luogu.com.cn/problem/P2824 问题思路 本文介绍一种二分答案的做法,时间复杂度为:(nm)*log(n)*log(n).本题存在nlog(n)的做法,然而其做法没有二分答案的做法通俗易懂. 默认读…...

echart在线图表demo下载直接运行
echart 全面的数据可视化图表解决方案 | 折线图、柱状图、饼图、散点图、水球图等各类图表展示 持续更新中 三色带下表题速度仪表盘 地图自定义图标 动态环形图饼状图 动态水波动圆形 多标题指针仪表盘 温度仪表盘带下标题 横向柱状图排名 环形饼状图 双折线趋势变化...

MLX5_SET_TO_ONES宏解析
看代码时,遇到一个非常复杂的宏MLX5_SET_TO_ONES,这个宏的主要作用是对特定的数据结构置位,宏的上下文如下: #define __mlx5_nullp(typ) ((struct mlx5_ifc_##typ##_bits *)0) #define __mlx5_bit_off(typ, fld) (offsetof(struc…...
SQL Server入门-SSMS简单使用(2008R2版)-1
环境: win10,SQL Server 2008 R2 参考: SQL Server 新建数据库 - 菜鸟教程 https://www.cainiaoya.com/sqlserver/sql-server-create-db.html 第 2 课:编写 Transact-SQL | Microsoft Learn https://learn.microsoft.com/zh-cn/…...

高考专业抉择探索计算机专业的未来展望及适合人群
身份:一位正在面临人生重要抉择的高考生,一位计算机行业从业者 正文: 随着2024年高考落幕,我与数百万高三学生一样,又将面临人生中的重要抉择:选择大学专业。对于许多学生来说,计算机科学…...

windows安装spark
在 Windows 上安装 Spark 并进行配置需要一些步骤,包括安装必要的软件和配置环境变量。以下是详细的步骤指南: 步骤一:安装 Java 下载和安装 Java Development Kit (JDK) 到 Oracle JDK 下载页面 或 OpenJDK 下载页面 下载适合你系统的 JDK。…...
【信息学奥赛】CSP-J/S初赛03 计算机网络与编程语言分类
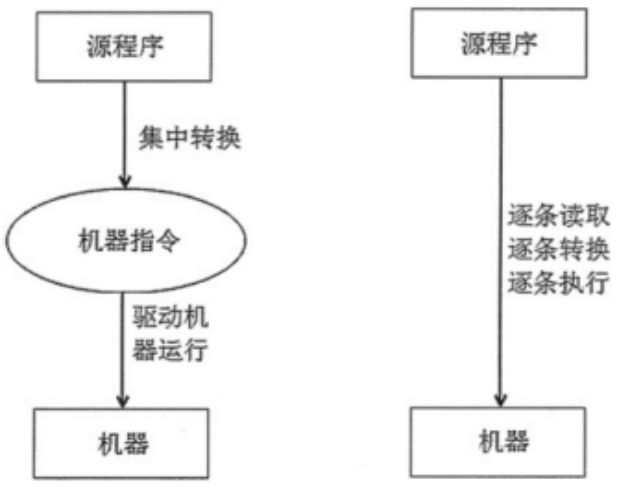
第1节 计算机网络基础 1.1 网络的定义 所谓计算机网络,就是利用通信线路和设备,把分布在不同地理位置上的多台计算机连 接起来。计算机网络是现代通信技术与计算机技术相结合的产物。 网络中计算机与计算机之间的通信依靠协议进行。协议是计算机收、发…...

python20 函数的定及调用
函数的定及调用 函数是将一段实现功能的完整代码,使用函数名称进行封装,通过函数名称进行调用。以此达到一次编写,多次调用的目的 用 def 关键字来声明 函数 格式: def 函数名(参数列表):函数体[:return 返回值是可选的࿰…...
【Android WebView】WebView基础
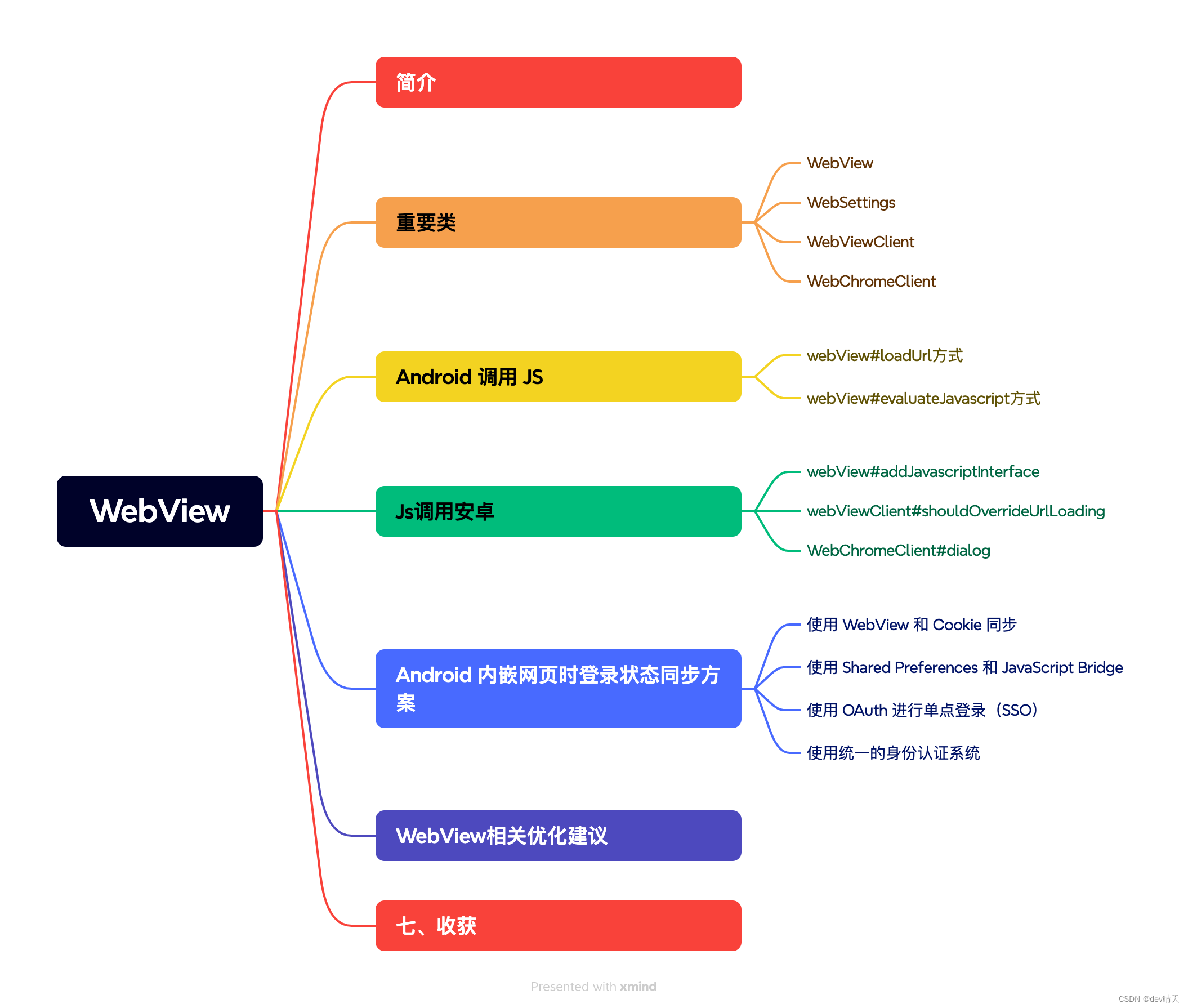
一、简介 WebView是一个基于webkit引擎、展现web页面的控件。Android的Webview在低版本和高版本采用了不同的webkit版本内核,4.4后直接使用了Chrome。 二、重要类 以WebView类为基础,WebSettings、WebViewClient、WebChromeClient为辅助共同完成安卓段加…...
Python酷库之旅-第三方库openpyxl(03)
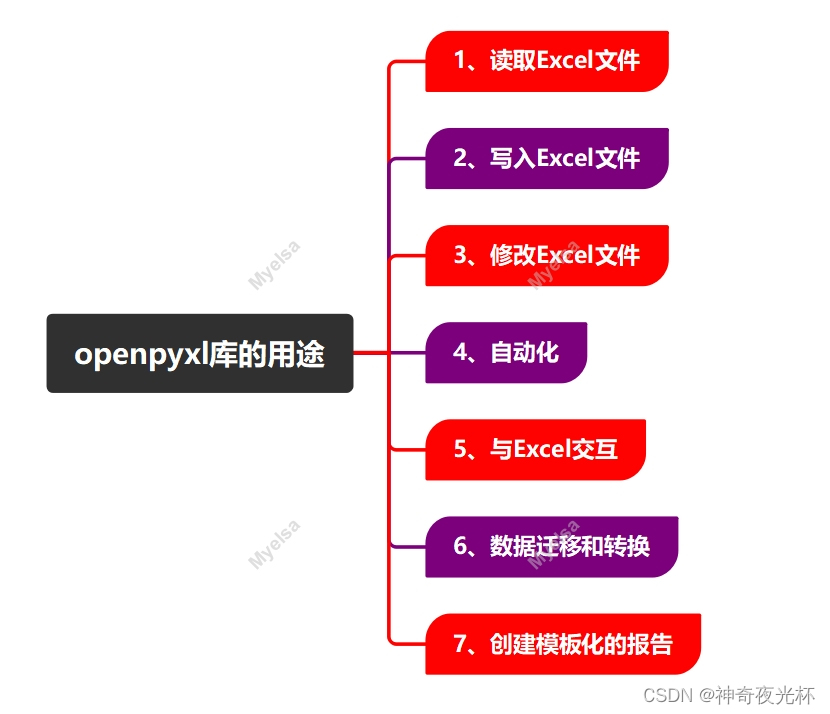
目录 一、 openpyxl库的由来 1、背景 2、起源 3、发展 4、特点 4-1、支持.xlsx格式 4-2、读写Excel文件 4-3、操作单元格 4-4、创建和修改工作表 4-5、样式设置 4-6、图表和公式 4-7、支持数字和日期格式 二、openpyxl库的优缺点 1、优点 1-1、支持现代Excel格式…...
电脑丢失dll文件一键修复的方法有哪些?分析dll文件修复的多种策略
我们经常会遇到各种各样的问题,其中之一就是DLL文件的丢失。DLL文件(动态链接库)是操作系统和应用程序正常运行所必需的文件,当这些文件丢失或损坏时,可能会导致软件无法正常启动,甚至影响系统的稳定性。对…...

小程序项目业务逻辑回忆4
用户查询积分 积分获取规则如下: 邀请其他用户购票参会,将获取该用户花费金额的10%获取积分。 邀请用户注册参观展览,需注册并现场签到,将获取10分的奖励积分。 邀请企业用户参展,将获取企业参展金额的5%获取到积分。 上述3条积分获取规…...
)
LeetCode 16.最接近的三数之和(C++)
链接 https://leetcode.cn/problems/3sum-closest/description/ 题目 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例1 输入&a…...

JSON.parse 解析NaN, Infinity, -Infinity失败
背景 JSON.parse() 方法解析字符串时, 如果字符串包含NaN, Infinity, -Infinity会报错。因为我们需要先将NaN, Infinity, -Infinity替换成字符类型,再做转换 解决方法 function convert(str) {str str.replace(/NaN/g, "NaN");str str.re…...

【计算机】我不允许还有人不知道数据库是什么
数据库是计算机科学中的一个核心概念,它是用于存储、检索、管理和处理数据的系统。在现代的软件开发和信息技术中,数据库扮演着至关重要的角色。以下是关于数据库的一些基本要点: 数据存储: 数据库提供了一个结构化的方式来存储数据,使得数据可以高效地组织和访问。它通过…...
制作WIFI二维码,实现一键扫描连接WIFI
在现代社会,Wi-Fi已成为我们日常生活中不可或缺的一部分。无论是在家庭、办公室还是公共场所,我们都希望能够快速方便地连接到Wi-Fi网络。下面小编就来和大家分享通过制作WIFI二维码,来实现一键扫描就可以连接WIFI的方法。连接WIFI不用在告诉…...
数据结构-图的基本概念
图的定义 图时由非空的顶点集合和一个描述顶点之间关系的集合组成。可以定义为: G表示一个图,V表示点集,E表示边集。集合E的每一个二元组都包含两个值和,表示…...
)
【HarmonyOS NEXT 】鸿蒙generateBarcode (码图生成)
本模块支持将字符串转换为二维码或条形码,目前已支持的码制式为EAN-8、EAN-13、UPC-A、UPC-E、Codabar、Code 39、Code 93、Code 128、ITF-14、QR Code、Data Matrix、PDF417、Aztec。暂时不支持多功能码生成。 起始版本:4.1.0(11) 导入模块 import {…...

python测试工程师 之 unittest框架总结
unittest 学习目标unittest 框架的基本使⽤⽅法(组成)断⾔的使⽤ (让程序⾃动的判断预期结果和实际结果是否相符)参数化(多个测试数据, 测试代码写⼀份 传参)⽣成测试报告 复习pythonunittest 框架的介绍核⼼要素(组成)1. TestCase 测试⽤例, 这个测试⽤例是 unittest 的组成部…...

微服务中的相关概念
Eureka Eureka 是由 Netflix 开发的一个服务发现和注册中心,广泛应用于微服务架构中。Eureka 主要用于管理和协调分布式服务的注册和发现,确保各个服务之间能够方便地找到并通信。它是 Netflix OSS(Netflix Open Source Software)…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
