解两道四年级奥数题(等差数列)玩玩
1、1~200这200个连续自然数的全部数字之和是________。
2、2,4,6,……,2008这些偶数的所有各位数字之和是________。
这两道题算易错吧,这里求数字之和,比如124这个数的全部数字之和是1+2+4=7。
两题数学解题思路一样,数字之和,数字无非就是0-9这10个数,要求和0可以忽略,所以就是1-9这九个数。那么我们只要算出每个数出现几次就可以了。
第一题:
1出现在个位数的情况有,1,11,21,...191,所以一共有(0,1,2,19)组一共出现20次。
同理2-9也是20次,所以个位数所有数字和为(1+2+...+9)*20=900。
1出现在十位数的情况有:(10,11,...19),(110,111,...119)两组,一组10个数,所以也出现20次。
同理2-9也是20次,所以十位数所有数字和为(1+2+...+9)*20=900。
1出现在百位数的情况有,100,101...199一共100次。
2出现在百位数的情况只有200一个。
所以百位数所有数字和为100*1+2=102。
综上,1~200这200个连续自然数的全部数字之和是:900+900+102=1902。
第二题:
个位数只能是偶数,所以:
2出现在个位数的情况有2,12,22,...2002,所以一共有(0,1,2,...200)组一共有201次。
同理4,6,8出现在个位数的情况为201次,所以所有个位数字之和为201*(2+4+6+8)=4020。
十位数开始可以奇数了,所以从1开始算:
1出现在十位数的情况有:(10,12,14,16,18),(110,112,114,116,118)...(1910,1912,19141916,1918),一共有(0,10,20...190)共20组5个数,也就是一共出现100次。
同理2,9也是100次,所以十位数所有数字和为(1+2+...+9)*100=4500。
1出现在百位数的情况有:(100,102,...198)(1100,1102,...1198)一共2组50个数,所以一共出现100次
同理2-9在百位也各出现100次,所以百位数所有数字和为(1+2+...+9)*100=4500。
1出现在千位数的情况有1000,1002,1004...1998一共出现500次
2出现在千位数的情况有2000,2002,...2008一共出现5次。
3-9没在千位数出现,所以千位数所有数字和为500*1+5*2=510。
综上,2,4,6,……,2008这些偶数的所有各位数字之和是4020+4500+4500+510=13530。
以上是数学的解法,下面用编程python的解法,python的解法主要是利用遍历每个数的所有数字和。代码如下:
第一题:
n = 0
r = 0while n < 200:n = n + 1r = r + n % 10 #累加所有个位数if 9 < n < 100:r =r + n // 10#累加所有两位数的十位数if n >= 100:r = r + n // 100 + n //10 % 10#累加所有三位数的百位数+十位数print(r)
第二题:
n = 0
r = 0while n < 2008:n = n + 2r = r + n % 10 #累加所有个位数if 9 < n < 100:r = r + n // 10#累加所有两位数的十位数if 100 <= n < 1000:r = r + n // 100 + n // 10 % 10 #累加所有三位数的百位数和十位数if n >= 1000:r = r + n // 1000 + n // 100 % 10 + n // 10 % 10 #累加所有四位数的千位数+百位数+十位数print(r)
相关文章:

解两道四年级奥数题(等差数列)玩玩
1、1~200这200个连续自然数的全部数字之和是________。 2、2,4,6,……,2008这些偶数的所有各位数字之和是________。 这两道题算易错吧,这里求数字之和,比如124这个数的全部数字之和是1247。 …...

深入理解Python中的并发与异步的结合使用
在上一篇文章中,我们讨论了异步编程中的性能优化技巧,并简单介绍了trio和curio库。今天,我们将深入探讨如何将并发编程与异步编程结合使用,并详细讲解如何利用trio和curio库优化异步编程中的性能。 文章目录 并发与异步编程的区…...

如何将 ChatGPT 集成到你的应用中
在当今快速发展的技术环境中,将人工智能聊天解决方案集成到你的应用程序中可以显著提升用户体验和参与度。OpenAI 的 ChatGPT 以其对话能力和高级语言理解而闻名,对于希望在其应用程序中实现智能聊天功能的开发人员来说是一个绝佳的选择。那我们今天就来…...

在 Swift 中,UILabel添加点击事件的方法
在 Swift 中,可以使用 UITapGestureRecognizer 给 UILabel 添加点击事件。以下是一个详细的步骤和示例代码: 1. 创建 UILabel 并添加到视图 在 Storyboard 或代码中创建一个 UILabel 并将其添加到视图中。 2. 启用 UILabel 的用户交互 默认情况下&am…...
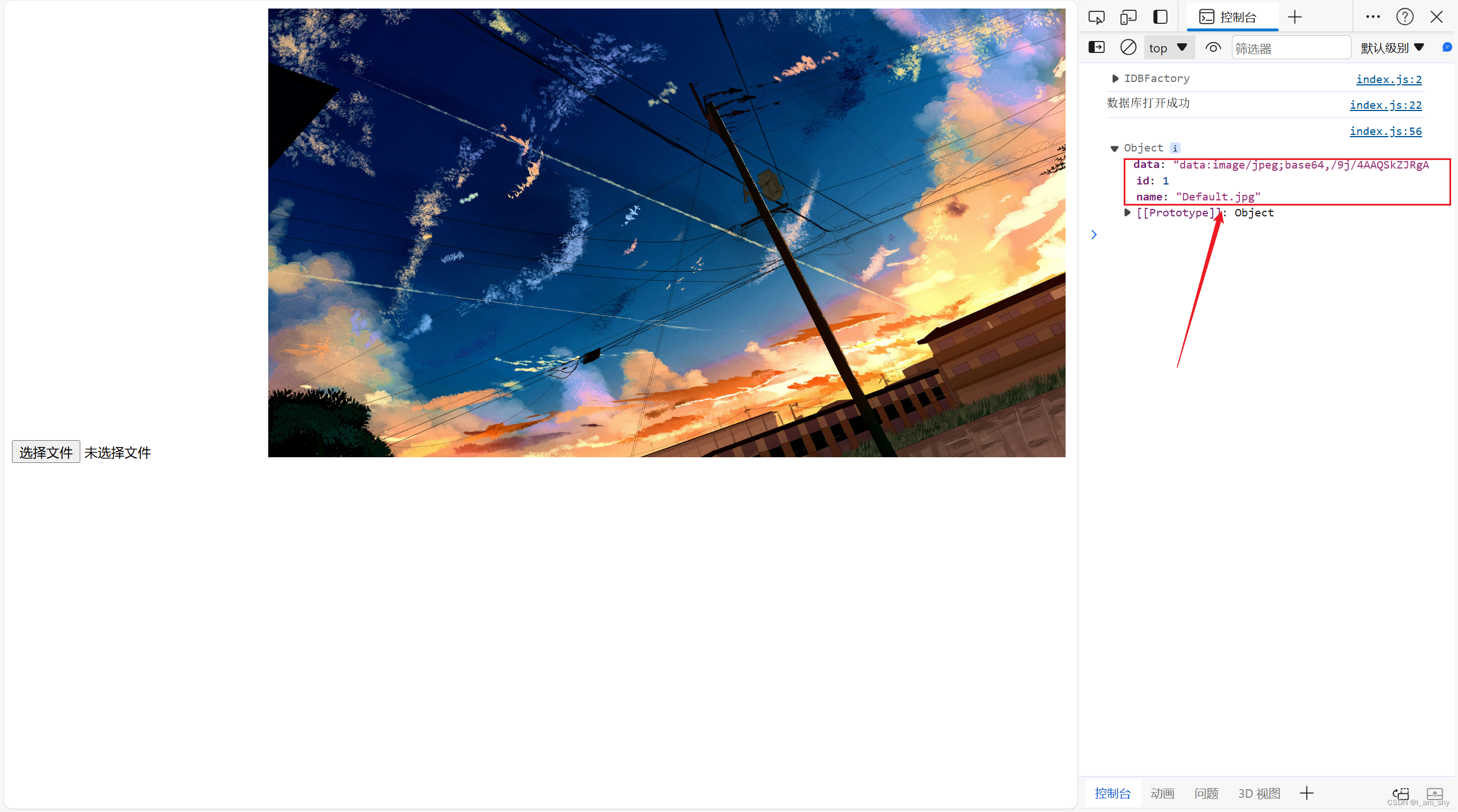
indexedDB---掌握浏览器内建数据库的基本用法
1.认识indexedDB IndexedDB 是一个浏览器内建的数据库,它可以存放对象格式的数据,类似本地存储localstore,但是相比localStore 10MB的存储量,indexedDB可存储的数据量远超过这个数值,具体是多少呢? 默认情…...
【css】如何修改input选中历史选项后,自动填充的蓝色背景色
自动填充前: 自动填充后: 解决办法 方法一:设置背景透明(通过拉长过渡时间,和延迟过渡开始时间,掩盖input自动填充背景颜色) PS:注意,这个过渡效果会在你的delay tim…...

红队内网攻防渗透:内网渗透之内网对抗:网络通讯篇防火墙组策略入站和出站规则单层双层C2正反向上线解决方案
红队内网攻防渗透 1. 内网网络通讯1.1 防火墙策略-入站规则&出站规则&自定义1.1.1 防火墙默认入站&出站策略1.1.2 防火墙自定义入站&出站策略1.1.3 内网域防火墙同步策略1.2 防火墙限制1.2.1 防火墙限制端口1.2.2 防火墙限制协议1.2.2.1 防火墙协议入站限制1.2…...

linux 查看进程启动方式
目录 如果是systemd管理的服务怎么快速找到对应的服务器呢 什么是CGroup 查找进程对应的systemd服务 方法一:查看 /proc//cgroup 文件 方法二:使用 ps 命令结合 --cgroup 选项 方法三:systemd-cgls 关于 system.slice 与 user.slice …...
基于Java实训中心管理系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟 感兴趣的可以先收藏起来,…...

第2章 Android应用的界面编程
🌈个人主页:小新_- 🎈个人座右铭:“成功者不是从不失败的人,而是从不放弃的人!”🎈 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 🏆所属专栏࿱…...

springboot学习-图灵课堂-最详细学习
springboot-repeat springBoot学习代码说明为什么java -jar springJar包后项目就可以启动 配置文件介绍 springBoot学习 依赖引入 <properties><project.build.sourceEncoding>UTF-8</project.build.sourceEncoding><maven.compiler.target>8</mav…...

Total CAD Converter与Total Excel Converter软件分享
1.软件介绍 Total CAD Converter Total CAD Converter 是一款功能强大的工具,能够将 CAD 文件转换为多种格式,如 PDF、TIFF、JPEG、BMP、WMF、PNG、DXF、BMP、CGM、HPGL、SVG、PS 和 SWF 等。其支持的源格式丰富多样,包括 dxf、dwg、dwf、d…...

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 启动多任务排序(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 启动多任务排序(200分) 🌍 评测功能需要订阅专栏后私信联系…...

【会议征稿,JPCS出版】第三届电力系统与能源技术国际学术会议(ICPSET 2024,7月5-7)
第三届电力系统与能源技术国际学术会议(ICPSET 2024)将于2024年7月5-7日在杭州举办。由浙江水利水电学院电机产业学院主办,AEIC学术交流中心承办,湖州市南浔创新研究院、南浔区科技局(科协)协办 。会议主要…...
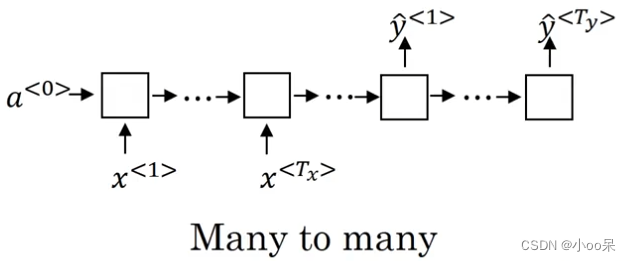
【机器学习300问】118、循环神经网络(RNN)的基本结构是怎样的?
将讲解循环神经网络RNN之前,我先抛出几个疑问:为什么发明循环神经网络?它的出现背景是怎样的?这些问题可以帮助我们更好的去理解RNN。下面我来逐一解答。 一、循环神经网络诞生的背景 循环神经网络(RNN)的…...

loveqq-framework 和 thymeleaf 整合遇到的 th:field 的坑,原来只有 spring 下才有效
相信大家在使用 thymeleaf 的时候,绝大部分都是和 springboot 一块儿使用的,所以 th:field 属性用的很舒服。 但实际上,th:field 只有在 spring 环境下下有用,单独的 thymeleaf 是不支持的! 为什么我知道呢ÿ…...

hugging face:大模型时代的github介绍
1. Hugging Face是什么: Hugging Face大模型时代的“github”,很多人有个这样的认知,但是我觉得不完全准确,他们相似的地方在于资源丰富,github有各种各样的软件代码和示例,但是它不是系统的,没…...

如何快速绘制logistic回归预测模型的ROC曲线?
临床预测模型,也是临床统计分析的一个大类,除了前期构建模型,还要对模型的预测能力、区分度、校准度、临床获益等方面展开评价,确保模型是有效的! 其中评价模型的好坏主要方面还是要看区分度和校准度,而区分…...

实现具有多个实现类的接口并为每个实现类定义一个名字的方法
在Java中,实现具有多个实现类的接口并为每个实现类定义一个名字的方法,可以通过使用工厂模式或服务定位器模式来完成。以下是使用工厂模式的一个示例: 定义接口和实现类 首先,定义一个接口和多个实现类: // 接口 publ…...

Linux解压缩命令
文章目录 前言1. tar - 打包和压缩文件2. gzip - 压缩文件3. gunzip - 解压缩gzip文件4. bzip2 - 压缩文件5. unzip - 解压缩zip文件6. zip - 压缩文件为zip格式7. 7z - 7-Zip压缩工具8. unrar - 解压缩RAR文件 前言 解压缩文件在Linux中是常见的任务,以下是一些常…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
