【线性代数】【一】1.6 矩阵的可逆性与线性方程组的解
文章目录
- 前言
- 一、求解逆矩阵
- 二、线性方程组的解的存在性
- 总结
前言
前文我们引入了逆矩阵的概念,紧接着我们就需要讨论一个矩阵逆的存在性以及如何求解这个逆矩阵。最后再回归上最初的线性方程组的解,分析其中的联系。
一、求解逆矩阵
我们先回想一下在1.3消去法的矩阵表示中,我们知道对一个系数矩阵做一些了的初等行变换,可以将矩阵变为上三角矩阵U。再往前一步,如果我们继续对U做初等行变换,那么我们最终可以得到一个单位矩阵 I I I或者是一个包含零行的对角矩阵(只有对角元素可能存在非零值,全零矩阵为特殊对角矩阵)。
首先第一种情况,变成单位矩阵,此时,我们可以把所有初等行变换所对应的矩阵累乘起来,表示为 B = E n E n − 1 . . . E 2 E 1 B=E_nE_{n-1}...E_2E_1 B=EnEn−1...E2E1,于是我们有 B A = I BA=I BA=I。也就是说, B B B就是我们想要找的系数矩阵 A A A的逆矩阵。
而另一种情况,存在零行,就说明在初等行变换的过程中,存在两行线性相关了,经过乘系数相减后就变为全零了。此时则不存在 A A A的逆矩阵。这个也很好说明:存在零行的矩阵,无论乘上什么矩阵,结果还会有零行,因此不可能为单位阵。而初等变换不改变矩阵的可逆性,因此不存在 A A A的逆矩阵。
因此我们可以归纳一下,如果矩阵中的两行线性相关了,则必然可以通过初等变换进行消去得到零行,而存在零行则必然不可逆。从而得到一个结论:矩阵中的行(列)向量若线性相关,则矩阵不可逆。 这里,有必要再重新定义一下线性相关:对于一组向量 a 1 , a 2 , . . . a n a_1,a_2,...a_n a1,a2,...an,都有 a 1 x 1 + a 2 x 2 + . . . a n x n = 0 a_1x_1+a_2x_2+...a_nx_n=0 a1x1+a2x2+...anxn=0当且仅当系数 x i x_i xi均为0时成立,则称这组向量线性无关,否则为线性相关。 这个结论似乎和我们之前说的略有出入,前面说的是两行线性相关,而给出的定义是讨论一组向量的线性相关。其实下面是更一般的情况,即使一组向量线性相关,其中也可以存在个别向量之间线性无关。
按照所给定义,而只要矩阵中的所有行向量线性相关,则根据定义必然可以找到一组非全零系数 a i a_i ai使得上述方程成立,也就是说明存在某一个行向量可以被其他行向量线性表示( a n = a 1 x 1 + a 2 x 2 + . . . a n − 1 x n − 1 a_n=a_1x_1+a_2x_2+...a_{n-1}x_{n-1} an=a1x1+a2x2+...an−1xn−1)。因此,我们可以通过初等变换,将该行向量化为零行。(按照线性表示系数的相反数,依次去作乘系数相加,最后该行会被完全消去, a n − a 1 x 1 − a 2 x 2 − . . . a n − 1 x n − 1 = 0 a_n-a_1x_1-a_2x_2-...a_{n-1}x_{n-1}=0 an−a1x1−a2x2−...an−1xn−1=0)也就是必然可以推导出零行。
反之,若线性无关,则没有任何一行向量可以被其他行向量线性表示,也就找不到任意一组系数对应的初等变换,可以完全消去该行,因此矩阵的行(列)向量线性无关则必然存在逆矩阵。
二、线性方程组的解的存在性
现在我们从刚刚所介绍的线性相关性的角度,再来审视一下线性方程组的解。我们要求方程组 A X = 0 AX=0 AX=0的解,就是要找到一组线性组合系数,将矩阵中的列向量进行线性组合后得到一个零向量。这不就是线性相关性的定义吗,如果这个方程组只要零向量的解,则说明所有列向量线性无关,反正则线性相关。因此,系数矩阵A为可逆矩阵 ↔ \leftrightarrow ↔矩阵中的列(行)向量线性无关 ↔ \leftrightarrow ↔线性方程组 A X = 0 AX=0 AX=0只有零解。
如果系数矩阵不可逆,则线性方程组必然存在非零解,且必然有无穷多个非零解。(即使只有一个向量可以被其他向量线性表示,也只需要对线性表示的系数同时乘上一个非零数,线性表示方程仍然成立,而乘上该非零数以后得到的x仍然是非零解。)
此外,关于 A X = b AX=b AX=b这种线性方程组的解,将在更加深入地讨论了线性相关性,矩阵的秩等内容后做深入分析。
总结
本文先从初等变换的角度,给出了判断矩阵可逆性以及求逆的方法,随后再给出了线性相关性的定义以及矩阵的可逆性、向量线性相关性、以及线性方程组的解的相关关系。
相关文章:

【线性代数】【一】1.6 矩阵的可逆性与线性方程组的解
文章目录 前言一、求解逆矩阵二、线性方程组的解的存在性总结 前言 前文我们引入了逆矩阵的概念,紧接着我们就需要讨论一个矩阵逆的存在性以及如何求解这个逆矩阵。最后再回归上最初的线性方程组的解,分析其中的联系。 一、求解逆矩阵 我们先回想一下在…...
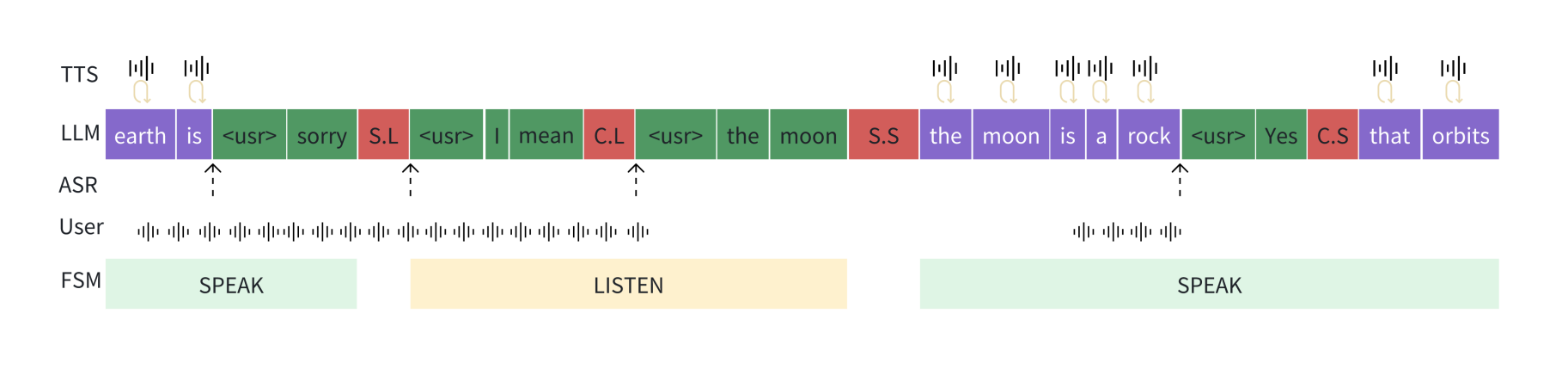
基于大型语言模型的全双工语音对话方案
摘要解读 我们提出了一种能够以全双工方式运行的生成性对话系统,实现了无缝互动。该系统基于一个精心调整的大型语言模型(LLM),使其能够感知模块、运动功能模块以及一个具有两种状态(称为神经有限状态机,n…...

Spring Boot集成Minio插件快速入门
1 Minio介绍 MinIO 是一个基于 Apache License v2.0 开源协议的对象存储服务。它兼容亚马逊 S3 云存储服务接口,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等,而一个对象文件可以是任意大小&…...

【C++新特性】右值引用
右值和右值的区别 C11 中右值可以分为两种:一个是将亡值( xvalue, expiring value),另一个则是纯右值( prvalue, PureRvalue): 纯右值:非引用返回的临时变量、运算表达式产生的临时变…...
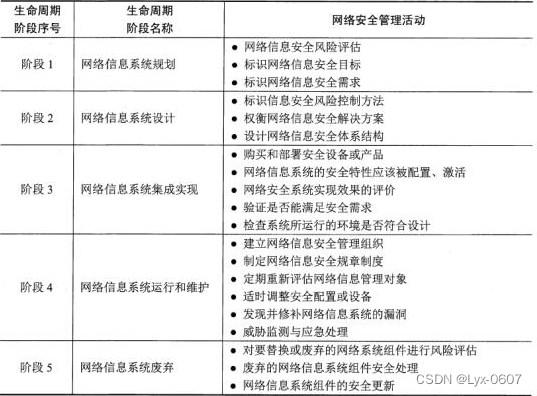
信息安全基础知识(完整)
信息安全基础知识 安全策略表达模型是一种对安全需求与安全策略的抽象概念表达,一般分为自主访问控制模型(HRU)和强制访问控制模型(BLP、Biba)IDS基本原理是通过分析网络行为(访问方式、访问量、与历史访问…...
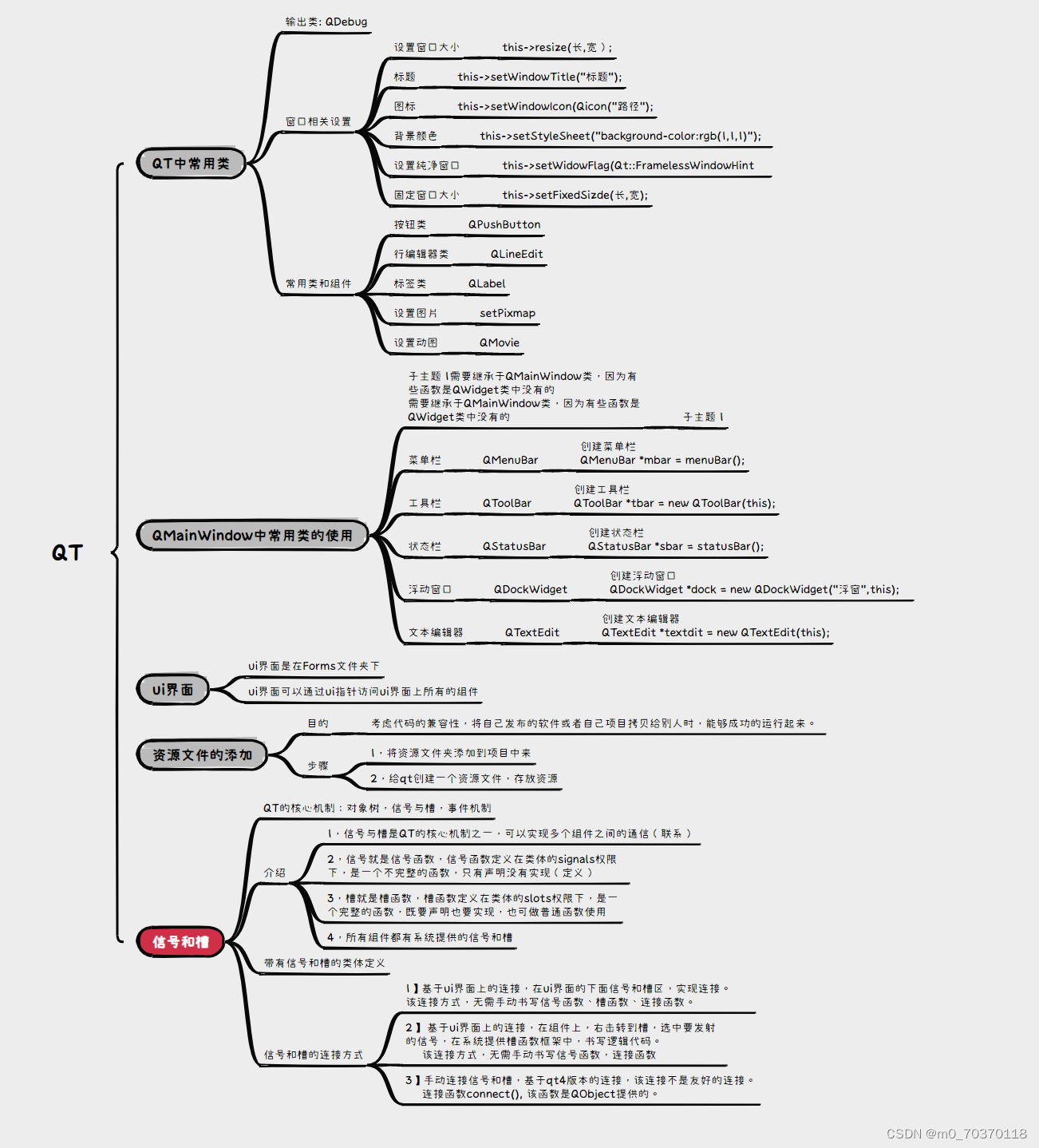
QT
#include "widget.h" #include "ui_widget.h" Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) ,Gcancle(new QPushButton("取消",this)) ,EmmEdit(new QLineEdit(this)) { ui->setupUi(this);…...

双例集合(三)——双例集合的实现类之TreeMap容器类
Map接口有两个实现类,一个是HashMap容器类,另一个是TreeMap容器类。TreeMap容器类的使用在API上于HashMap容器类没有太大的区别。它们的区别主要体现在两个方面,一个是底层实现方式上,HashMap是基于Hash算法来实现的吗,…...

[SAP ABAP] 运算符
1.算数运算符 算术运算符描述加法-减法*乘法/除法MOD取余 示例1 输出结果: 输出结果: 2.比较运算符 比较运算符描述示例 等于 A B A EQ B <> 不等于 A <> B A NE B >大于 A > B A GT B <小于 A < B A LT B >大于或等于 A > B A GE B <小…...
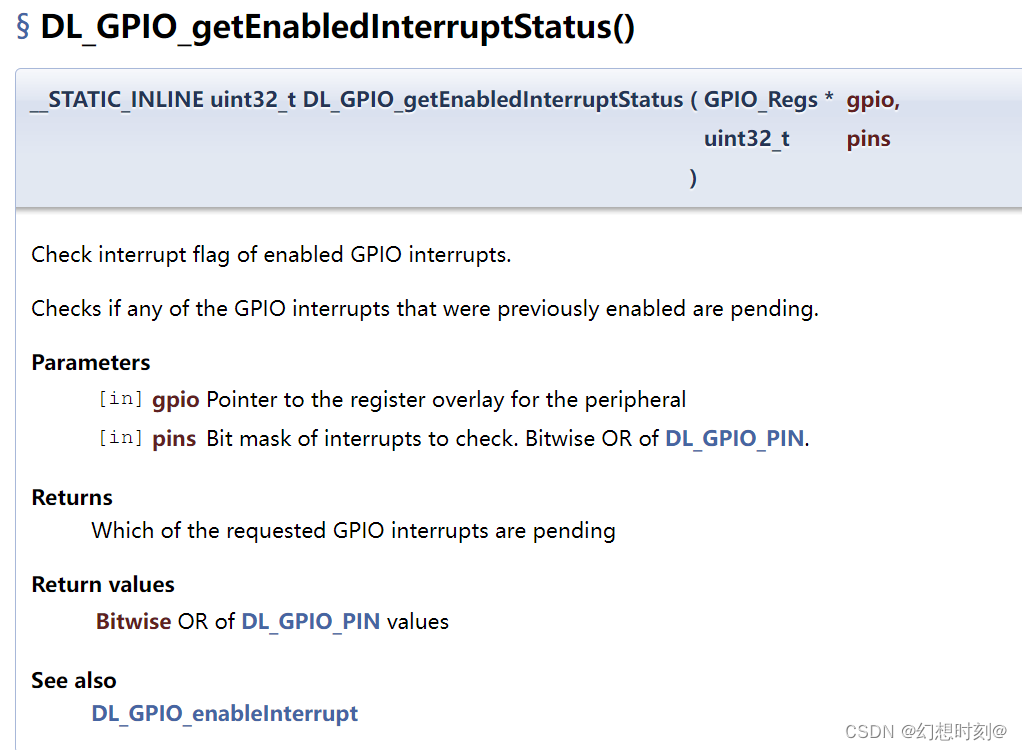
MSPM0G3507 ——GPIO例程讲解2——simultaneous_interrupts
主函数: #include "ti_msp_dl_config.h"int main(void) {SYSCFG_DL_init();/* Enable Interrupt for both GPIOA and GPIOB ports */NVIC_EnableIRQ(GPIO_SWITCHES_GPIOA_INT_IRQN); //启用SWITCHES——A的中断 NVIC_EnableIRQ(GPIO_S…...

某程序员:30岁了,老婆管钱,背着我买了50万股票,亏了20w,强制她清仓后又买了36万
“辛辛苦苦攒了几年钱,本想买房买车,结果全被老婆炒股亏掉了!” 近日,一位30岁的程序员大哥在网上吐苦水,引发了网友们的热议。 这位程序员大哥和妻子结婚后,一直秉持着“男主外,女主内”的传统…...

Docker常见面试题整理
文章目录 1. Docker 是什么?它解决了什么问题?2. Docker 和虚拟机(VM)的区别是什么?3、Docker三个核心概念4、如何构建一个 Docker 镜像?5、如何将一个 Docker 容器连接到多个网络?6、Docker Co…...
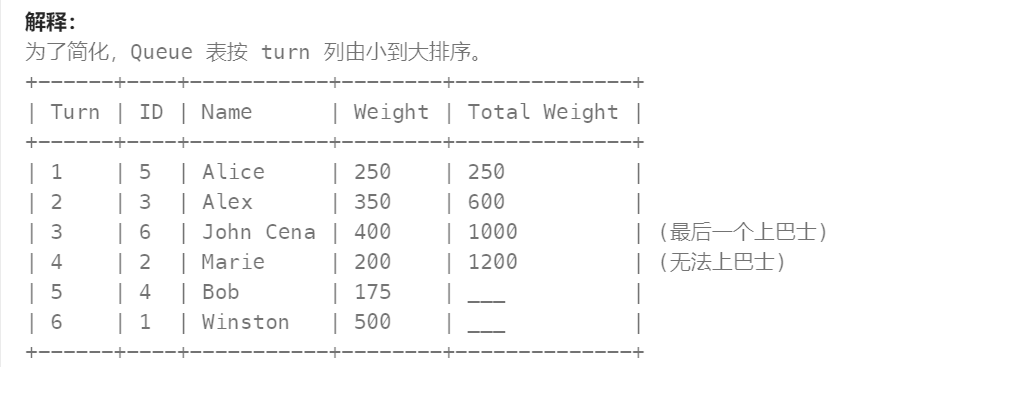
35 - 最后一个能进入巴士的人(高频 SQL 50 题基础版)
35 - 最后一个能进入巴士的人 -- sum(weight) over(order by turn) as total,根据turn升序,再求前面数的和 selectperson_name from(selectperson_name,sum(weight) over(order by turn) as totalfromQueue) new_Queue wheretotal<1000 order by total desc lim…...

WPF将dll文件嵌入到exe文件中
WPF将dll文件嵌入到exe文件中 第一步:打开.csproj文件,在Import节点后添加如下代码: <Target Name"AfterResolveReferences"><ItemGroup><EmbeddedResource Include"(ReferenceCopyLocalPaths)" Condit…...
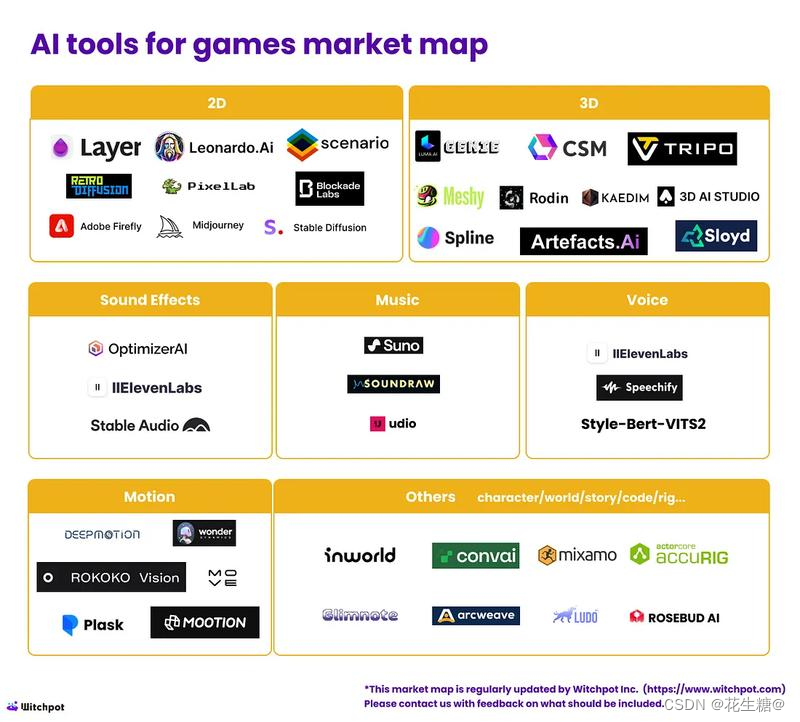
2024年AI+游戏赛道的公司和工具归类总结
随着人工智能技术的飞速发展,AI在游戏开发领域的应用越来越广泛。以下是对2024年AI+游戏赛道的公司和工具的归类总结,涵盖了从角色和场景设计到音频制作,再到动作捕捉和动画生成等多个方面。 2D与3D创作 2D创作工具:专注于角色和场景的平面设计,提供AI辅助的图案生成和风…...
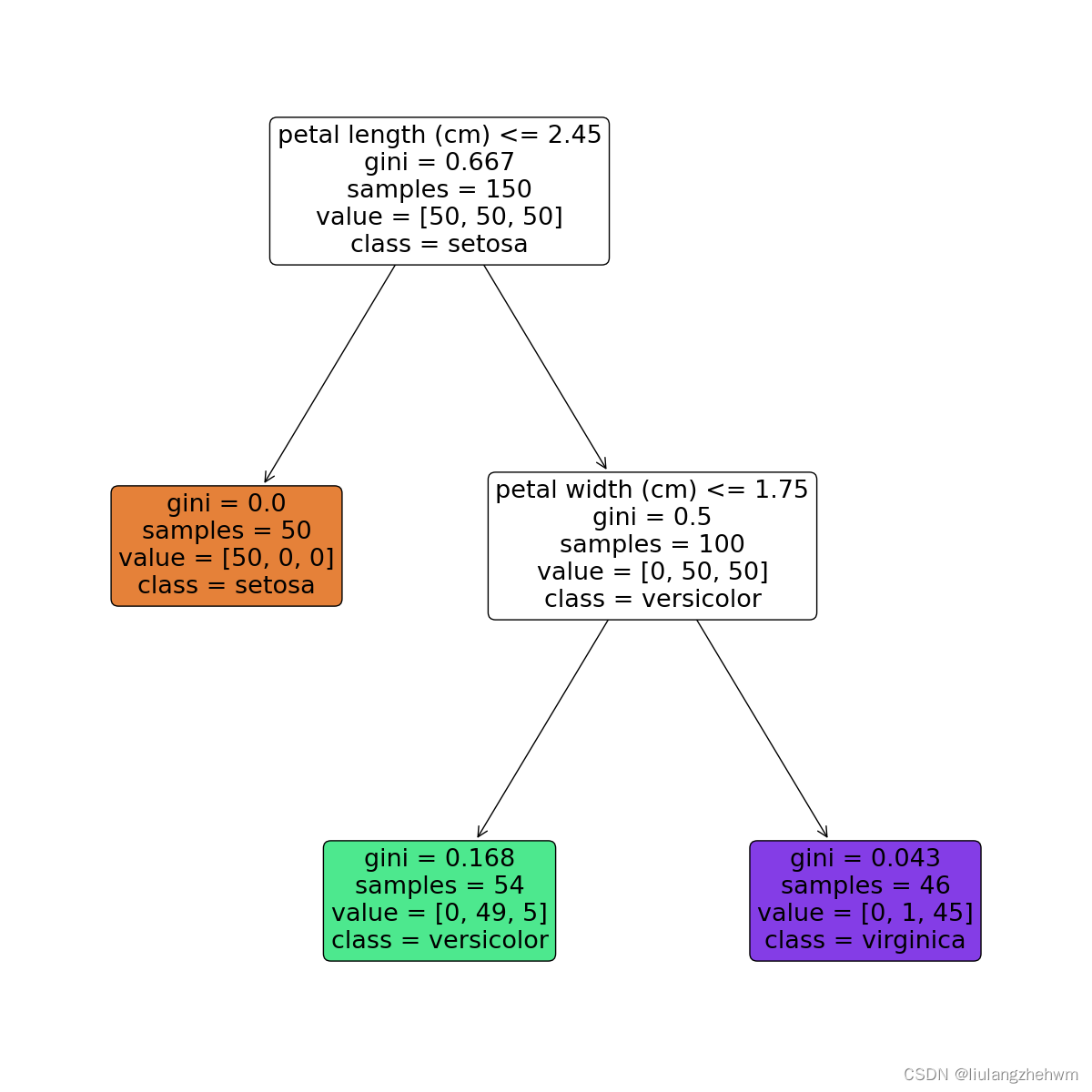
svm和决策树基本知识以及模型评价以及模型保存
svm和决策树基本知识以及模型评价以及模型保存 文章目录 一、SVM1.1,常用属性函数 二、决策树2.1,常用属性函数2.2,决策树可视化2.3,决策树解释 3,模型评价3.1,方面一(评价指标)3.2&…...

C++ 79 之 自己写异常类
#include <iostream> #include <string> using namespace std;class MyOutOfRange : public exception{ // 选中exception右键 转到定义 复制一份 virtual const char* what() const _GLIBCXX_TXN_SAFE_DYN _GLIBCXX_NOTHROW 进行函数重写 public: string m_msg;M…...

如何搭建一个成功的短剧制作平台
要搭建一个成功的短剧制作平台,需要考虑多个方面,包括目标定位、技术选择、内容管理、用户体验等。 1、明确目标和定位: 确定你的目标受众是谁,他们的年龄、兴趣、消费习惯等。 明确短剧制作平台的主要定位,是提供原创…...
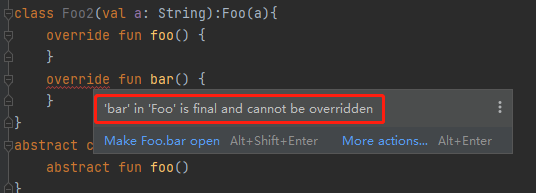
kotlin类
一、定义 1、kotlin中使用关键字class 声明类,如果一个类没有类体,也可以省略花括号, 默认为public 类型的: // 这段代码定义了一个公开的、不可被继承的Test类 class Test{} // 没有类体,可以省略花括号 class Test 底层代码&…...
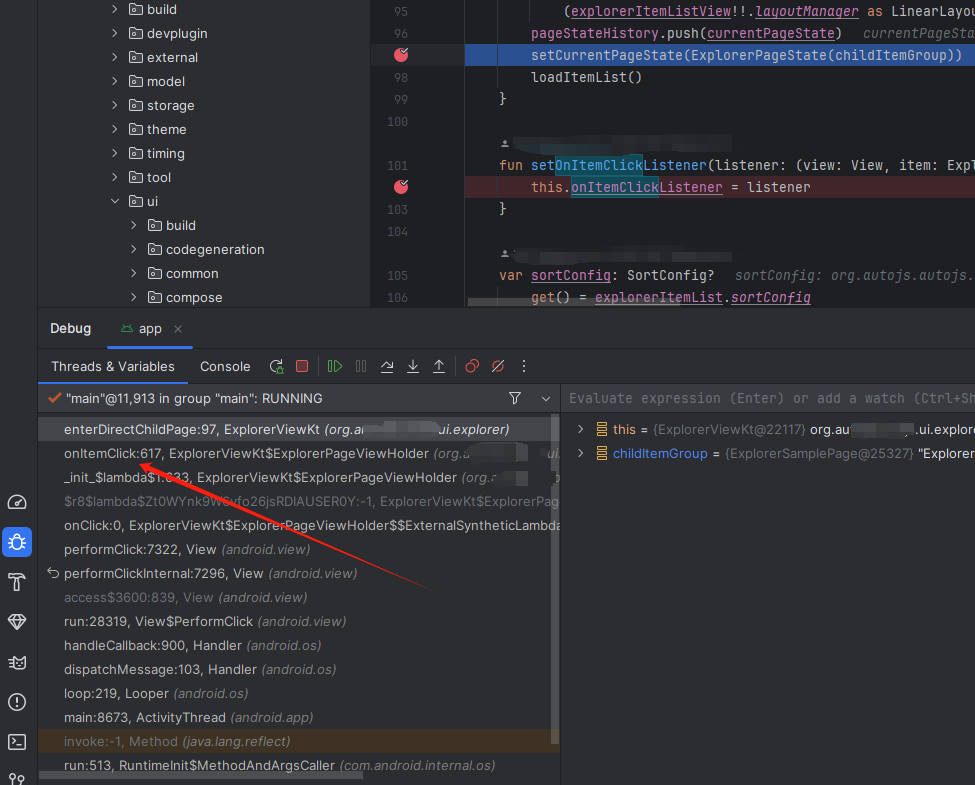
android | studio的UI布局和代码调试 | UI调试 (用于找到项目源码)
网上找到一个项目,想快速的搞懂是怎么实现的,搞了半天发现原来android都升级到Jetpack Compose了,然后去找源码挺不容易的,摸索中发现了这个调试的方法,还可以。 https://developer.android.com/studio/debug/layout-i…...
——ConfigurableField)
LangChain实战技巧之六:一起玩转config(上篇)——ConfigurableField
简介 Config 包含两大类内容, ConfigurableField 可配置的字段 configurable_alternatives 可配置的替代方案 分别使用两篇文章来给大家介绍,本篇先介绍ConfigurableField 常规介绍 一些资料会这样介绍 model_spec model.configurable_fields(model…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
