微积分-导数1(导数与变化率)
切线
要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线,我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x)),然后求出割线 P Q PQ PQ的斜率:
m P Q = f ( x ) − f ( a ) x − a m_{PQ} = \frac{f(x) - f(a)}{x - a} mPQ=x−af(x)−f(a)
当 Q Q Q沿着曲线向 P P P逐渐靠近, m P Q m_{PQ} mPQ会越来越接近切线的斜率 m m m。
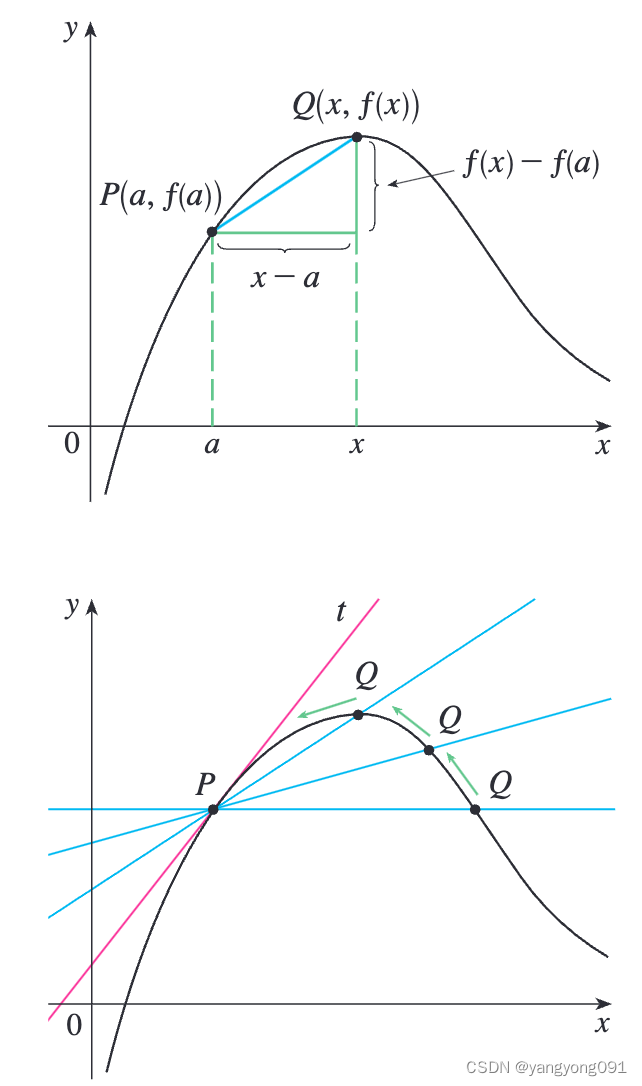
定义 1:与曲线 f ( x ) f(x) f(x)切于点 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))的切线是一条穿过 P P P的直线,其斜率为:
m = lim x → a f ( x ) − f ( a ) x − a m = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} m=x→alimx−af(x)−f(a)
例一
求抛物线 y = x 2 y = x^2 y=x2在点 P ( 1 , 1 ) P(1, 1) P(1,1)的切线公式。
解:
已知 a = 1 a = 1 a=1和 f ( x ) = x 2 f(x) = x^2 f(x)=x2,因此切线的斜率为:
m = lim x → 1 f ( x ) − f ( 1 ) x − 1 = lim x → 1 x 2 − 1 x − 1 = lim x → 1 ( x − 1 ) ( x + 1 ) x − 1 = lim x → 1 ( x + 1 ) = 1 + 1 = 2 \begin{align*} m &= \lim_{x \to 1} \frac{f(x) - f(1)}{x - 1} \\ &= \lim_{x \to 1} \frac{x^2 - 1}{x - 1} \\ &= \lim_{x \to 1} \frac{(x - 1)(x + 1)}{x - 1} \\ &= \lim_{x \to 1} (x + 1) \\ &= 1 + 1 = 2 \end{align*} m=x→1limx−1f(x)−f(1)=x→1limx−1x2−1=x→1limx−1(x−1)(x+1)=x→1lim(x+1)=1+1=2
再使用切点式,有
y − 1 = 2 ( x − 1 ) y = 2 x − 1 \begin{align*} y - 1 &= 2(x - 1) \\ y &= 2x - 1 \end{align*} y−1y=2(x−1)=2x−1
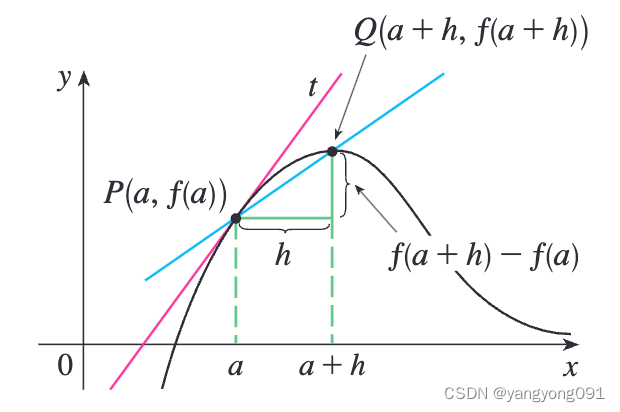
除定义中给出的求切线斜率的表达式之外,还有用下面的表达式 2求切线斜率:
m = lim h → 0 f ( a + h ) − f ( a ) h m = \lim_{{h \to 0}} \frac{{f(a + h) - f(a)}}{h} m=h→0limhf(a+h)−f(a)
例二
求双曲线 y = 3 / x y = 3/x y=3/x在点 ( 3 , 1 ) (3, 1) (3,1)的切线方程。
根据表达式2有
m = lim h → 0 f ( 3 + h ) − f ( 3 ) h = lim h → 0 ( 3 3 + h − 1 h ) = lim h → 0 ( 3 − ( 3 + h ) 3 + h h ) = lim h → 0 ( − h h ( 3 + h ) ) = lim h → 0 ( − 1 3 + h ) = − 1 3 \begin{align*} m &= \lim_{{h \to 0}} \frac{f(3 + h) - f(3)}{h} \\ &= \lim_{{h \to 0}} \left( \frac{\frac{3}{3 + h} - 1}{h} \right) \\ &= \lim_{{h \to 0}} \left( \frac{\frac{3 - (3 + h)}{3 + h}}{h} \right) \\ &= \lim_{{h \to 0}} \left( \frac{-h}{h(3 + h)} \right) \\ &= \lim_{{h \to 0}} \left( \frac{-1}{3 + h} \right) \\ &= -\frac{1}{3} \end{align*} m=h→0limhf(3+h)−f(3)=h→0lim(h3+h3−1)=h→0lim(h3+h3−(3+h))=h→0lim(h(3+h)−h)=h→0lim(3+h−1)=−31
速度
已知路程和时间的关系式 f ( x ) f(x) f(x),可以通过下面的表达式求位置 P P P和 Q Q Q之间移动的平均速度:
f ( a + h ) − f ( a ) h \frac{f(a+h) - f(a)}{h} hf(a+h)−f(a)
现在假设我们计算越来越短的时间间隔 ([a, a+h]) 上的平均速度。换句话说,我们让 (h) 趋近于 0。就像在下落的球的例子中一样,我们定义在时间 (t=a) 时的速度(或瞬时速度)(v(a)) 为这些平均速度的极限:
v ( a ) = lim h → 0 f ( a + h ) − f ( a ) h v(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} v(a)=h→0limhf(a+h)−f(a)
例三
假设一个球从CN塔上层观景台(距地面450米)掉下。
(a) 球在5秒钟后的速度是多少?
(b) 球撞到地面时的速度是多少?
提示:自由落体运动的公式为 s ( t ) = 1 2 g t 2 s(t) = \frac{1}{2} g t^2 s(t)=21gt2。
导数
导数定义:一个函数 f f f在某个数 a a a处的导数,记作 f ’ ( a ) f’(a) f’(a),定义为:
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h f{\prime}(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} f′(a)=h→0limhf(a+h)−f(a)
这个极限,如果存在,就被称为函数 f f f在点 a a a处的导数,它表示函数 f f f在 a a a处的瞬时变化率或斜率。也可以用下面的方程表示:
f ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a f{\prime}(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} f′(a)=x→alimx−af(x)−f(a)
例四
找到函数 f ( x ) = x 2 + 8 x + 19 f(x) = x^2 + 8x + 19 f(x)=x2+8x+19在数 a a a处的导数。
根据切线和导数的定义,我们可以得出一个结论:切线在点 ( a , f ( a ) ) (a, f(a)) (a,f(a))的斜率等于导数 f ′ ( a ) f{\prime}(a) f′(a)。
如果我们使用直线的点斜式方程,我们可以写出曲线 y = f ( x ) y = f(x) y=f(x)在点 ( a , f ( a ) ) (a, f(a)) (a,f(a))处的切线方程: y − f ( a ) = f ′ ( a ) ( x − a ) y - f(a) = f'(a)(x - a) y−f(a)=f′(a)(x−a)
例五
找到抛物线 y = x 2 + 8 x + 19 y = x^2 + 8x + 19 y=x2+8x+19在点 ( 3 , − 6 ) (3, -6) (3,−6)处的切线方程。
变化率
假设 y y y是 x x x的函数,我们写作 y = f ( x ) y = f(x) y=f(x)。如果 x x x从 x 1 x_1 x1变化到 x 2 x_2 x2,那么 x x x的变化量(也称为 x x x的增量)是
Δ x = x 2 − x 1 \Delta x = x_2 - x_1 Δx=x2−x1
相应地 y y y的变化量是
Δ y = f ( x 2 ) − f ( x 1 ) \Delta y = f(x_2) - f(x_1) Δy=f(x2)−f(x1)
商
Δ y Δ x = f ( x 2 ) − f ( x 1 ) x 2 − x 1 \frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} ΔxΔy=x2−x1f(x2)−f(x1)
被称为 y y y相对于 x x x在区间 [ x 1 , x 2 ] [x_1, x_2] [x1,x2]上的平均变化率,可以解释为图中割线 P Q PQ PQ的斜率。
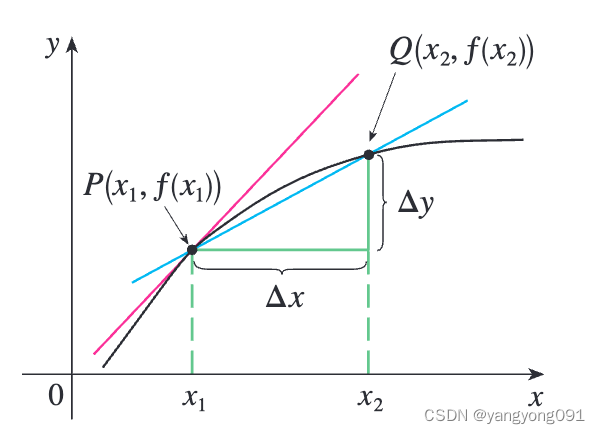
通过与速度类比,我们通过让 x 2 x_2 x2趋近 x 1 x_1 x1,从而让 Δ x \Delta x Δx趋近0,来考虑在越来越小的区间上的平均变化率。这些平均变化率的极限称为 y y y相对于 x x x在 x = x 1 x = x_1 x=x1处的瞬时变化率,它(与速度的情况一样)被解释为曲线 y = f ( x ) y = f(x) y=f(x)在点 P ( x 1 , f ( x 1 ) ) P(x_1, f(x_1)) P(x1,f(x1))处的切线的斜率:
lim Δ x → 0 Δ y Δ x = lim x 2 → x 1 f ( x 2 ) − f ( x 1 ) x 2 − x 1 \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1} Δx→0limΔxΔy=x2→x1limx2−x1f(x2)−f(x1)
前面我们已经知道,导数 f ′ ( a ) f'(a) f′(a)是曲线 y = f ( x ) y = f(x) y=f(x)在 x = a x = a x=a处的切线的斜率。现在我们知道切线的斜率就是瞬时变化率,因此可以说:导数 f ′ ( a ) f'(a) f′(a)是 y = f ( x ) y = f(x) y=f(x)在 x = a x = a x=a处的瞬时变化率。
如果我们绘制曲线 y = f ( x ) y = f(x) y=f(x),那么瞬时变化率就是该曲线在 x = a x = a x=a处的切线的斜率。这意味着,当导数很大时(因此曲线很陡,如图中的点P), y y y值变化很快。当导数很小时,曲线相对平缓(如点Q), y y y值变化缓慢。
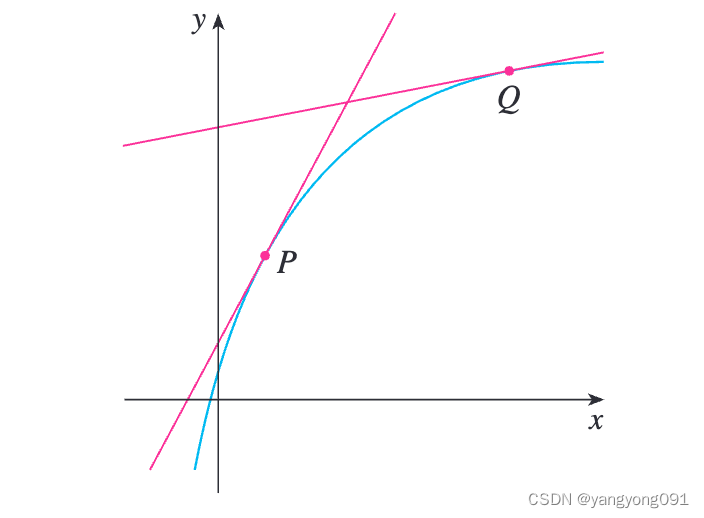
例六
制造商生产固定宽度的织物卷,生产 x x x 码织物的成本是 C ( x ) C(x) C(x) 美元。
(a) 导数 f ’ ( x ) f’(x) f’(x) 的含义是什么?它的单位是什么?
(b) 在实际中,说 f ’ ( 1000 ) = 9 f’(1000) = 9 f’(1000)=9 是什么意思?
(c) 你认为哪个大, f ’ ( 50 ) f’(50) f’(50) 还是 f ’ ( 500 ) f’(500) f’(500)或 f ’ ( 5000 ) f’(5000) f’(5000) 呢?
例七
让 D ( t ) D(t) D(t)表示时间 t t t时的美国国债。表格提供了从1985年到2010年每年底的估算值,单位为十亿美元。解释并估算 D ′ ( 2000 ) D\prime(2000) D′(2000)的值。
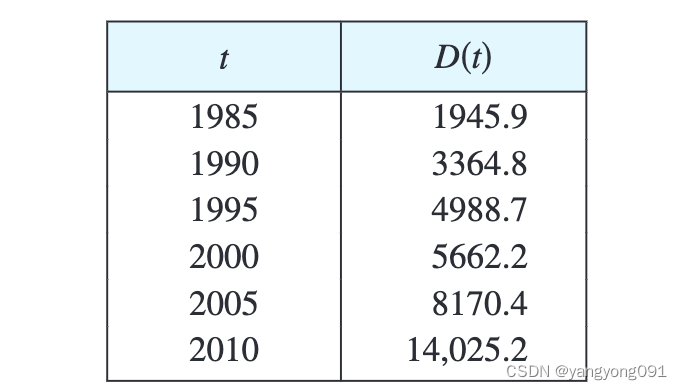
解:
导数 D ’ ( 2000 ) D’(2000) D’(2000) 表示国债 D D D 相对于时间 t t t 在 t = 2000 t = 2000 t=2000 时的变化率,即2000年国债的增长率。根据变化率方程有
D ′ ( 2000 ) = lim t → 2000 D ( t ) − D ( 2000 ) t − 2000 D{\prime}(2000) = \lim_{t \to 2000} \frac{D(t) - D(2000)}{t - 2000} D′(2000)=t→2000limt−2000D(t)−D(2000)
因此,我们计算并列出差商(平均变化率)的数值如下。
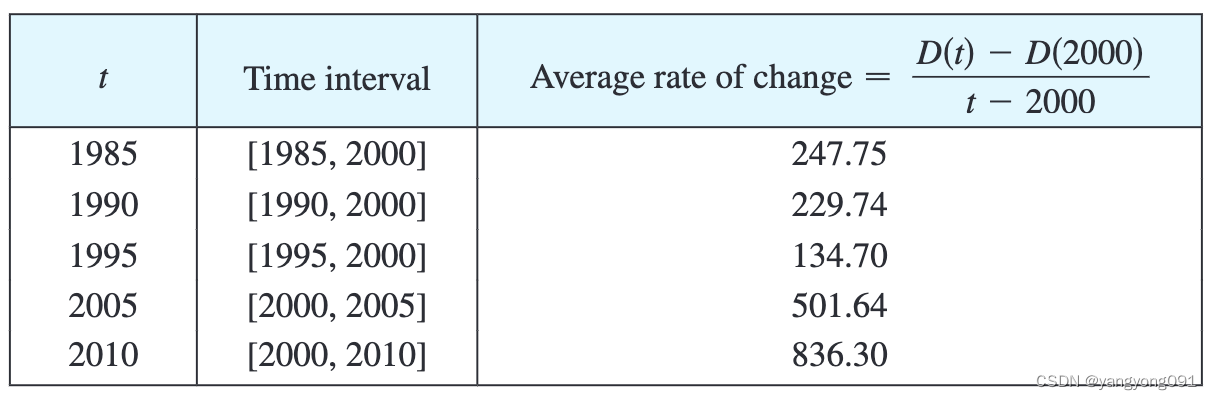
从这张表格中我们可以看出, D ′ ( 2000 ) D{\prime}(2000) D′(2000)大约在每年 134.7 134.7 134.7亿到 501.64 501.64 501.64亿美元之间。【在这里,我们做出一个合理的假设,即债务在1995年到2005年之间没有剧烈波动。】我们估计美国国债在2000年的增长率大约是这两个数字的平均值,即 D ′ ( 2000 ) ≈ 318 亿美元每年 D'(2000) \approx 318亿美元每年 D′(2000)≈318亿美元每年
相关文章:

微积分-导数1(导数与变化率)
切线 要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线,我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x)),然后求出割线 P Q PQ PQ的斜率: m P Q f ( x ) − f ( a ) x − a m_{PQ} \…...

最新PHP仿猪八戒任务威客网整站源码/在线接任务网站源码
资源介绍 老规矩,截图为亲测,前后台显示正常,细节功能未测,有兴趣的自己下载。 PHP仿猪八戒整站源码下载,phpmysql环境。威客开源建站系统,其主要交易对象是以用户为主的技能、经验、时间和智慧型商品。经…...
Windows安装配置jdk和maven
他妈的远程连接不上公司电脑,只能在家重新配置一遍,在此记录一下后端环境全部配置 Windows安装配置JDK 1.8一、下载 JDK 1.8二、配置环境变量三、验证安装 Windows安装配置Maven 3.8.8一、下载安装 Maven并配置环境变量二、设置仓库镜像及本地仓库三、测…...

电子SOP实施(MQTT协议)
架构图 服务与程序 用docker启动mqtt broker(服务器) 访问:http://192.168.88.173:18083/#/dashboard/overview 用户名:admin 密码:*** 消息发布者(查找sop的url地址,发布出去) 修改url,重新发布消息 import ran…...

【Unity导航系统】Navigation组件的概念及其使用示例
Unity中的NavMeshObstacle组件是一个用于动态障碍物的组件,它可以实时地影响导航网格(NavMesh)。当游戏对象附加了NavMeshObstacle组件时,它可以在AI进行路径规划时被识别为障碍物,从而让AI避开这些动态变化的障碍。 …...
vue-cli 根据文字生成pdf格式文件 jsPDF
1.安装jspdf npm install jspdf --save 2.下载ttf格式文件 也可以用C:\Windows\Fonts下的字体文件,反正调一个需要的ttf字体文件就行,但有的字体存在部分字体乱码现象 微软雅黑ttf下载地址: FontsMarket.com - Download Microsoft YaHei …...

【嵌入式DIY实例】-Nokia 5110显示DS3231 RTC数据
Nokia 5110显示DS3231 RTC数据 文章目录 Nokia 5110显示DS3231 RTC数据1、硬件准备与接线2、代码实现本文将介绍如何使用 ESP8266 NodeMCU 板和 DS3231 RTC 模块制作一个简单的数字实时时钟,其中可以使用连接到 NodeMCU 的两个按钮设置时间和日期,并将它们打印在诺基亚 5110 …...

【十三】图解mybatis缓存模块之装饰器模式
图解mybatis缓存模块之装饰器模式 简介 之前有写过一篇博客介绍过mybatis的缓存模块设计【九】mybatis 缓存模块设计-CSDN博客 ,当时着重讲解的是mybatis种一级缓存和二级缓存,本次博客补充讲解一下装饰器模式的应用,本篇主要分两部分讲解&a…...
字节大神强推千页PDF学习笔记,弱化学历问题,已拿意向书字节提前批移动端!
主要问java,以及虚拟机,问了一点android 1.实习项目有关的介绍以及问题回答 2.反射与代理的区别,动态代理,静态代理,二者的区别,以及代理模式的UML图 3.字节码技术 4.虚拟机的双亲委派,以及好…...

Python爬虫-贝壳二手房“改进版”
前言 本文是该专栏的第31篇,后面会持续分享python爬虫干货知识,记得关注。 在本专栏之前的文章《Python爬虫-贝壳二手房》中,笔者有详细介绍,基于python爬虫采集对应城市的二手房数据。 而在本文,笔者将基于该项目案例的基础上,进行一个项目代码的“改进版”。 具体实…...

zookeeper学习、配置文件参数详解
zookeeper学习、配置文件参数详解 zookeeper 配置文件参数详解tickTime 、session 的过期时间、maxSessionTimeout 三者之间的关系initLimit,syncLimit什么区别minSessionTimeout 默认值,**他的单位是ms** zookeeper 配置文件参数详解 ZooKeeper 是一个分布式协调服…...

SVG 模糊效果
SVG 模糊效果 SVG(Scalable Vector Graphics,可缩放矢量图形)是一种基于XML的图像格式,用于描述二维图形。它是一种矢量图形格式,因此可以无限放大而不失真。SVG广泛应用于网页设计、动画制作和图形编辑等领域。本文将介绍SVG中一种特殊的效果——模糊效果,以及如何使用…...
Electron+vite+vuetify项目搭建
最近想用Electron来进行跨平台的桌面应用开发。同时想用vuetify作为组件,于是想搭建一个这样的开发环境。其中踩了不少坑,总是会出现各种的编译错误和问题,依赖的各种问题,搞了好久最终环境终于弄好可正常开发了。这里分享下快速搭…...

洛谷:P1085 [NOIP2004 普及组] 不高兴的津津
1. 题目链接 https://www.luogu.com.cn/problem/P1085 P1085 [NOIP2004 普及组] 不高兴的津津 2. 题目描述 题目描述:津津每天要上课还要上辅导班,每天学习超过8小时就不开心,帮忙检查下津津的下周日程安排,然后告诉我她哪天不高…...
Webpack4从入门到精通以及和webpack5对比_webpack现在用的是哪个版本
3.1 打包样式资源css-loader、style-loader… {// 匹配哪些文件test: /\.less$/,// 使用哪些loader进行处理use: [// use数组中loader执行顺序:从右到左,从下到上,依次执行(先执行css-loader)// style-loader:创建style标签&#…...

巴鲁夫MacroBuilder2.0.0.0软件巴鲁夫和使用手侧
巴鲁夫MacroBuilder2.0.0.0软件巴鲁夫和使用手侧...
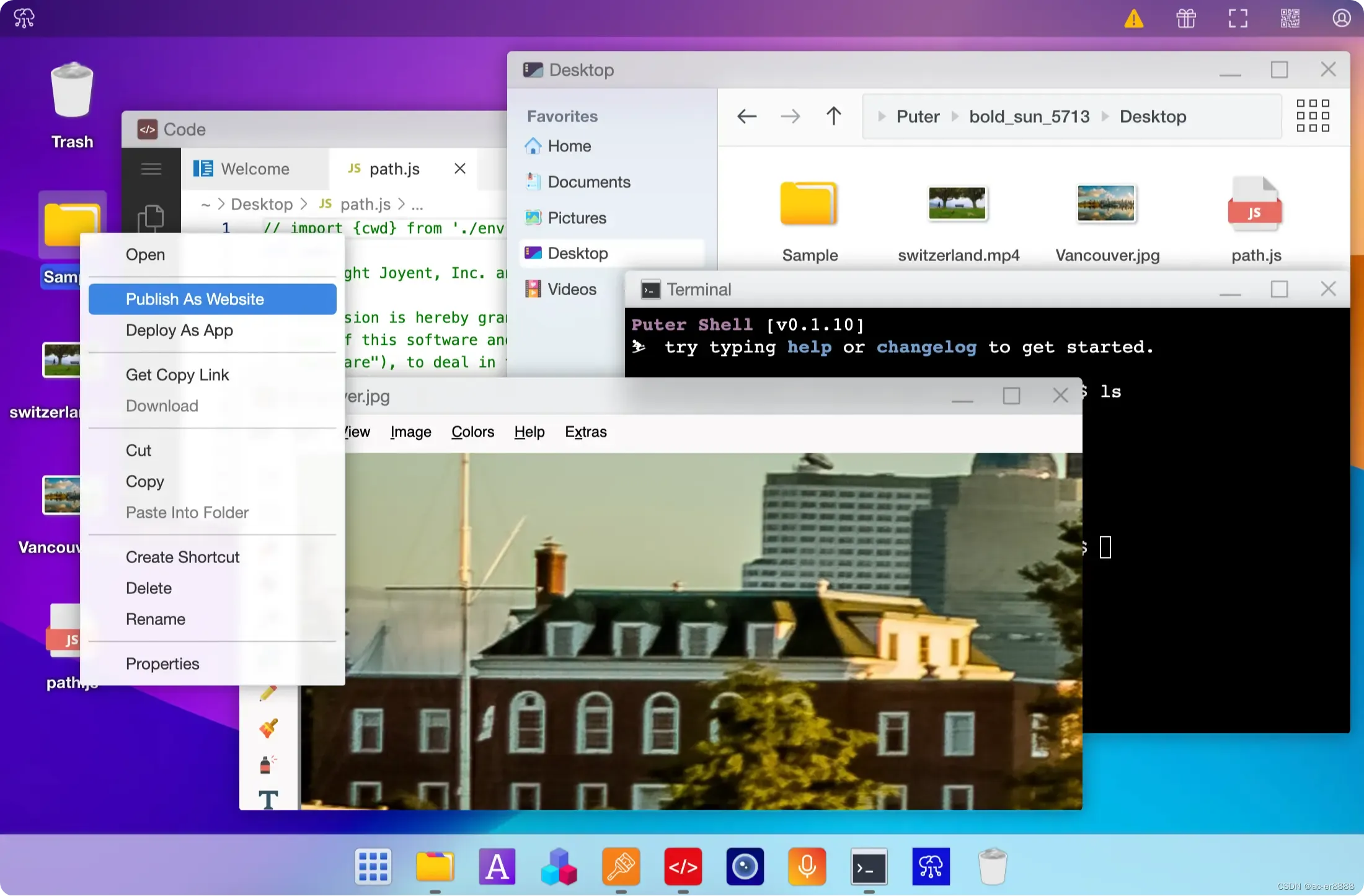
分享:Javascript开源桌面环境-Puter
Puter这是一个运行在浏览器里的桌面操作系统,提供了笔记本、代码编辑器、终端、画图、相机、录音等应用和一些小游戏。该项目作者出于性能方面的考虑没有选择 Vue 和 React 技术栈,而是采用的 JavaScript 和 jQuery 构建,支持 Docker 一键部署…...
【idea-jdk1.8】使用Spring Initializr 创建 Spring Boot项目没有JDK8
信息差真可怕! 很久没创建springboot项目,今天使用idea的Spring Initializr 创建 Spring Boot项目时,发现java版本里,无法选择jdk1.8,只有17、21、22;前段时间也听说过,springboot将放弃java8&a…...
)
647. 回文子串(leetcode)
647. 回文子串(leetcode) 题目描述 给你一个字符串 s ,请你统计并返回这个字符串中回文子串的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 示例1 输入:s “abc” 输出…...

【车载开发系列】汽车嵌入式开发常用工具介绍
【车载开发系列】汽车嵌入式开发常用工具介绍 【车载开发系列】汽车嵌入式开发常用工具介绍 【车载开发系列】汽车嵌入式开发常用工具介绍一. ChipON IDE For KungFu32二. ChipON PRO KF32三. GIT四. JLink五. S32DS六. parasoft ctest七. TCANLINPro八. vector Canoe 一. Chip…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
