华为HCIP Datacom H12-821 卷5
1.单选题
下列哪种工具不能被 route-policy 的 apply 子句直接引用?
A、IP-Prefix
B、tag
C、community
D、origin
正确答案： A
解析：
因route-policy工具中， apply 后面跟的是路由的相关属性。 但是ip-prefix是用来匹配路由的工具。
2.单选题
相关文章：
华为HCIP Datacom H12-821 卷5
1.单选题 下列哪种工具不能被 route-policy 的 apply 子句直接引用? A、IP-Prefix B、tag C、community D、origin 正确答案： A 解析： 因route-policy工具中， apply 后面跟的是路由的相关属性。 但是ip-prefix是用来匹配路由的工具。 2.单选题...
Mongodb数据库基本操作
本文为在命令行模式下Mongodb数据库的基本操作整理。 目录 数据库操作 创建数据库 查看所有数据 查看当前数据库 删除数据库 断开连接 查看命令api 集合操作 查看当前数据库下集合 创建集合 删除当前数据库中的集合 文档操作 插入文档 insertOne()方法 insertMa…...
【机器学习】基于Softmax松弛技术的离散数据采样
1.引言 1.1.离散数据采样的意义 离散数据采样在深度学习中起着至关重要的作用，它直接影响到模型的性能、泛化能力、训练效率、鲁棒性和解释性。 首先，采样方法能够有效地平衡数据集中不同类别的样本数量，使得模型在训练时能够更均衡地学习…...
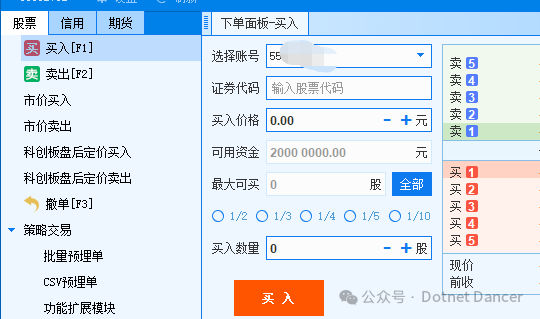
.NET+Python量化【1】——环境部署和个人资金账户信息查询
前言：量化资料很少，.NET更少。那我就来开个先河吧~ 以下是使用QMT进行量化开发的环境部署和基础信息获取有关操作。 1、首先自己申请券商的QMT权限，此步骤省略。 2、登陆QMT，选择极简模式，或者独立交易模式之类的。会进…...
洛谷 P10584 [蓝桥杯 2024 国 A] 数学题（整除分块+杜教筛）
题目 思路来源 登录 - Luogu Spilopelia 题解 参考了两篇洛谷题解，第一篇能得出这个式子，第二篇有比较严格的复杂度分析 结合去年蓝桥杯洛谷P9238，基本就能得出这题的正确做法 代码 #include<bits/stdc.h> #include<iostream&g…...
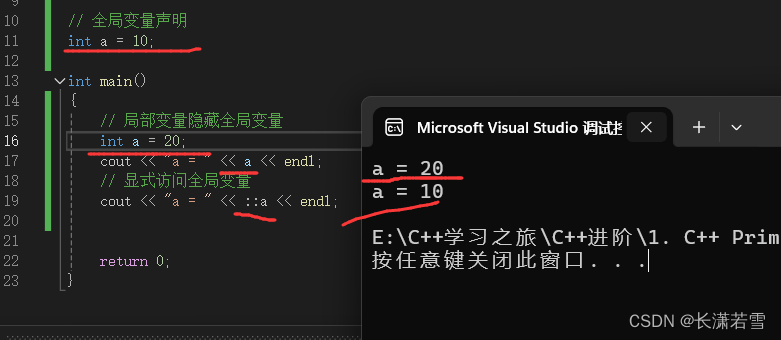
深入讲解C++基础知识（一）
目录 一、基本内置类型1. 类型的作用2. 分类3. 整型3.1 内存描述及查询3.2 布尔类型 —— bool3.3 字符类型 —— char3.4 其他整型 4. 有符号类型和无符号类型5. 浮点型6. 如何选择类型7. 类型转换7.1 自动类型转换7.2 强制类型转换7.3 类型转换总结 8. 类型溢出8.1 注意事项 …...
Python爬虫实战：批量下载网站图片
1.获取图片的url链接 首先，打开百度图片首页，注意下图url中的index 接着，把页面切换成传统翻页版（flip），因为这样有利于我们爬取图片！ 对比了几个url发现，pn参数是请求到的数量。…...
使用 JavaScript 获取电池状态
在现代的移动设备和笔记本电脑上，了解电池状态是一项非常有用的功能。使用 JavaScript 可以轻松地获取电池的充电状态、电量百分比等信息。本文将介绍如何使用 JavaScript 访问这些信息，并将其显示在网页上。 1. HTML 结构 首先，我们需要一…...
java—类反射机制
简述 反射机制允许程序在执行期间借助于Reflection API取得任何类的内部信息（如成员变量，构造器，成员方法等），并能操作对象的属性及方法。反射机制在设计模式和框架底层都能用到。 类一旦加载，在堆中会产生…...
浏览器-服务器架构 (BS架构) 详解
目录 前言1. BS架构概述1.1 BS架构的定义1.2 BS架构的基本原理 2. BS架构的优势2.1 客户端简化2.2 易于更新和维护2.3 跨平台性强2.4 扩展性高 3. BS架构的劣势3.1 网络依赖性强3.2 安全性问题3.3 用户体验局限 4. BS架构的典型应用场景4.1 企业内部应用4.2 电子商务平台4.3 在…...
微型操作系统内核源码详解系列五（四）：cm3下svc启动任务
系列一：微型操作系统内核源码详解系列一：rtos内核源码概论篇（以freertos为例）-CSDN博客 系列二：微型操作系统内核源码详解系列二：数据结构和对象篇（以freertos为例）-CSDN博客 系列…...
筛质数（暴力法、埃氏筛、欧拉筛）
筛质数（暴力法、埃氏筛、欧拉筛） 暴力法 思路分析： 直接双for循环来求解质数 如果不设置标记只是简单地执行了break会导致内部循环(由j控制)而不是立即打印i或者跳过它。如果打印语句写到内部循环中，也会导致每个 非素数也被打…...
使用USI作为主SPI接口
代码; lcd_drive.c //***************************************************************************** // // File........: LCD_driver.c // // Author(s)...: ATMEL Norway // // Target(s)...: ATmega169 // // Compiler....: AVR-GCC 3.3.1; avr-libc 1.0 // // D…...
AI播客下载：Eye on AI（AI深度洞察）
"Eye on A.I." 是一档双周播客节目，由长期担任《纽约时报》记者的 Craig S. Smith 主持。在每一集中，Craig 都会与在人工智能领域产生影响的人们交谈。该播客的目的是将渐进的进步置于更广阔的背景中，并考虑发展中的技术的全球影响…...
Flink 窗口触发器
参考： NoteWarehouse/05_BigData/09_Flink(1).md at main FGL12321/NoteWarehouse GitHub Flink系列 9. 介绍 Flink 窗口触发器、移除器和延迟数据等 | hnbian https://github.com/kinoxyz1/bigdata-learning-notes/blob/master/note/flink/Window%26%E6%97%B6…...
Java面试题：解释线程间如何通过wait、notify和notifyAll方法进行通信
在 Java 中，线程间的通信可以通过 wait()、notify() 和 notifyAll() 这三个方法实现。这些方法是 Java 线程 Thread 类的一部分，它们与 synchronized 关键字一起使用，以实现线程间的协调。 基本概念 wait()：当一个线程执行到 wa…...
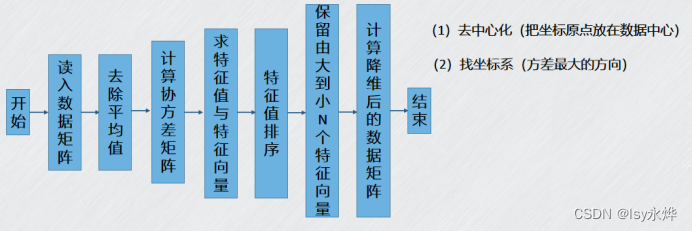
【机器学习 复习】第9章 降维算法——PCA降维
一、概念 1.PCA （1）主成分分析（Principal ComponentAnalysis，PCA）一种经典的线性降维分析算法。 （2）原理，这里以二维转一维为例，原来的平面变成了一条直线 这是三维变二…...
Ubuntu系统docker gpu环境搭建
Ubuntu系统dockergpu环境搭建 安装步骤前置安装安装指定版本的依赖包用docker官方脚本安装Docker-ce添加稳定仓库和GPG秘钥更新源 安装docker安装nvidia-docker2重启docker服务阿里云镜像加速 相关命令网络 docker常用命令镜像容器 docker相关问题解决方案使用wsl时docker的容器…...
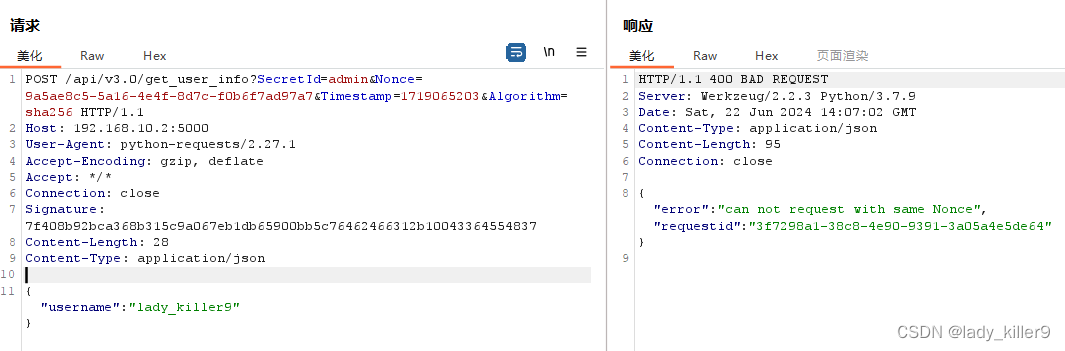
网络安全-如何设计一个安全的API（安全角度）
目录 API安全概述设计一个安全的API一个基本的API主要代码调用API的一些问题 BasicAuth认证流程主要代码问题 API Key流程主要代码问题 Bearer auth/Token auth流程 Digest Auth流程主要代码问题 JWT Token流程代码问题 Hmac流程主要代码问题 OAuth比较自定义请求签名身份认证&…...
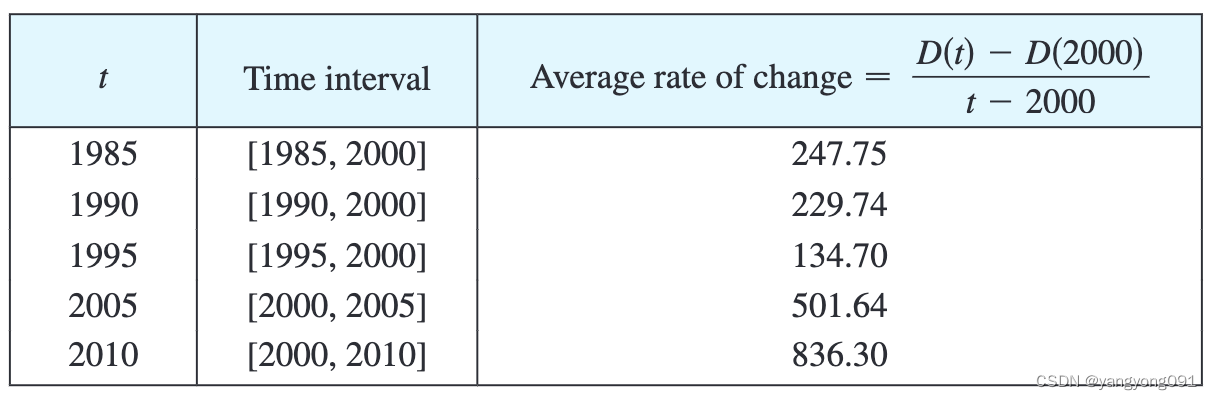
微积分-导数1（导数与变化率）
切线 要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线，我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x))，然后求出割线 P Q PQ PQ的斜率： m P Q f ( x ) − f ( a ) x − a m_{PQ} \…...
Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展：显示创建时间8. 功能扩展：记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
练习（含atoi的模拟实现,自定义类型等练习）
一、结构体大小的计算及位段 （结构体大小计算及位段 详解请看：自定义类型：结构体进阶-CSDN博客） 1.在32位系统环境，编译选项为4字节对齐，那么sizeof(A)和sizeof(B)是多少？ #pragma pack(4)st…...
Cesium1.95中高性能加载1500个点
一、基本方式： 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06（十亿美元）。漏洞扫描服务市场行业预计将从 2024 年的 3.48（十亿美元）增长到 2032 年的 9.54（十亿美元）。预测期内漏洞扫描服务市场 CAGR（增长率&…...
vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径：src/utils/timer.ts 完整代码： import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
零基础设计模式——行为型模式 - 责任链模式
第四部分：行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习！行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想：使多个对象都有机会处…...
重启Eureka集群中的节点，对已经注册的服务有什么影响
先看答案，如果正确地操作，重启Eureka集群中的节点，对已经注册的服务影响非常小，甚至可以做到无感知。 但如果操作不当，可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
AirSim/Cosys-AirSim 游戏开发（四）外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机，因为在使用过程中发现 Airsim 对外部监控相机的描述模糊，而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置，最后在源码示例中找到了，所以感…...
Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋，无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话，配置.bahs_profile后也能解决上下翻页这些，但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可，…...