Representation RL:HarmonyDream: Task Harmonization Inside World Models
ICML2024
paper
code
Intro
基于状态表征的model-based强化学习方法一般需要学习状态转移模型以及奖励模型。现有方法都是将二者联合训练但普遍缺乏对如何平衡二者之间的比重进行研究。本文提出的HarmonyDream便是通过自动调整损失系数来维持任务间的和谐,即在世界模型学习过程中保持观测状态建模和奖励建模之间的动态平衡。
Method
算法基于DreamV2的世界模型架构:
- Representation model: z t ∼ q θ ( z t ∣ z t − 1 , a t − 1 , o t ) z_{t}\sim q_{\theta }( z_{t}\mid z_{t- 1}, a_{t- 1}, o_{t}) zt∼qθ(zt∣zt−1,at−1,ot)
- Observation model: o ^ t ∼ p θ ( o ^ t ∣ z t ) \hat{o}_t\sim p_\theta(\hat{o}_t\mid z_t) o^t∼pθ(o^t∣zt)
- Transition model: z ^ t ∼ p θ ( z ^ t ∣ z t − 1 , a t − 1 ) \hat{z} _t\sim p_\theta ( \hat{z} _t\mid z_{t- 1}, a_{t- 1}) z^t∼pθ(z^t∣zt−1,at−1)
- Reward model: r ^ t ∼ p θ ( r ^ t ∣ z t ) . \hat{r}_t\sim p_\theta\left(\hat{r}_t\mid z_t\right). r^t∼pθ(r^t∣zt).
所有参数通过联合训练以下三个损失函数
- Observation loss: L o ( θ ) = − log p θ ( o t ∣ z t ) \mathcal{L}_o(\theta)=-\log p_\theta(o_t\mid z_t) Lo(θ)=−logpθ(ot∣zt)
- Reward loss: L r ( θ ) = − log p θ ( r t ∣ z t ) \mathcal{L}_{r}(\theta)=-\log p_{\theta}(r_{t}\mid z_{t}) Lr(θ)=−logpθ(rt∣zt)
- Dynamics loss: L d ( θ ) = K L [ q θ ( z t ∣ z t − 1 , a t − 1 , o t ) ∥ p θ ( z ^ t ∣ z t − 1 , a t − 1 ) ] \mathcal{L}_{d}(\theta)=KL[q_{\theta}(z_{t}\mid z_{t-1},a_{t-1},o_{t})\parallel p_{\theta}(\hat{z}_{t}\mid z_{t-1},a_{t-1})] Ld(θ)=KL[qθ(zt∣zt−1,at−1,ot)∥pθ(z^t∣zt−1,at−1)],
对三种目标加权后便是最终优化目标
L ( θ ) = w o L o ( θ ) + w r L r ( θ ) + w d L d ( θ ) . \mathcal{L}(\theta)=w_o\mathcal{L}_o(\theta)+w_r\mathcal{L}_r(\theta)+w_d\mathcal{L}_d(\theta). L(θ)=woLo(θ)+wrLr(θ)+wdLd(θ).
HarmonyDream提出动态加权方法,
L ( θ , σ o , σ r , σ d ) = ∑ i ∈ { o , r , d } H ^ ( L i ( θ ) , σ i ) (5) = ∑ i ∈ { o , r , d } 1 σ i L i ( θ ) + log ( 1 + σ i ) . \begin{aligned} \mathcal{L}(\theta,\sigma_{o},\sigma_{r},\sigma_{d})& =\sum_{i\in\{o,r,d\}}\hat{\mathcal{H}}(\mathcal{L}_{i}(\theta),\sigma_{i}) \\ &&\text{(5)} \\ &=\sum_{i\in\{o,r,d\}}\frac{1}{\sigma_{i}}\mathcal{L}_{i}(\theta)+\log{(1+\sigma_{i})}. \end{aligned} L(θ,σo,σr,σd)=i∈{o,r,d}∑H^(Li(θ),σi)=i∈{o,r,d}∑σi1Li(θ)+log(1+σi).(5)
其中 σ i \sigma_i σi由 σ i = exp ( s i ) > 0 \sigma_i=\exp(s_i)>0 σi=exp(si)>0表示,源码中 s s s为一个可梯度回传的参数且初始化为0。
self.harmony_s1 = torch.nn.Parameter(-torch.log(torch.tensor(1.0))) #reward
self.harmony_s2 = torch.nn.Parameter(-torch.log(torch.tensor(1.0))) # image
self.harmony_s3 = torch.nn.Parameter(-torch.log(torch.tensor(1.0))) # kl
结果

相较于DreamerV2提升明显。结合DreamerV3的效果也很好。
相关文章:

Representation RL:HarmonyDream: Task Harmonization Inside World Models
ICML2024 paper code Intro 基于状态表征的model-based强化学习方法一般需要学习状态转移模型以及奖励模型。现有方法都是将二者联合训练但普遍缺乏对如何平衡二者之间的比重进行研究。本文提出的HarmonyDream便是通过自动调整损失系数来维持任务间的和谐,即在世界…...
Centos7系统下Docker的安装与配置
文章目录 前言下载Docker安装yum库安装Docker启动和校验配置Docker镜像加速卸载Docker 前言 此博客的内容的为自己的学习笔记,如果需要更具体的内容,可查看Docker官网文档内容 注意:以下命令在root管理员用户下运行,如果在普通用…...

无人机校企合作
有没有想过,无人机和校企合作能碰撞出怎样的火花?🔥今天就来给大家揭秘一下这个神秘组合! 无人机,作为现代科技的代表,已经渗透到我们生活的方方面面。而校企合作,更是推动科技创新、培养人才的…...
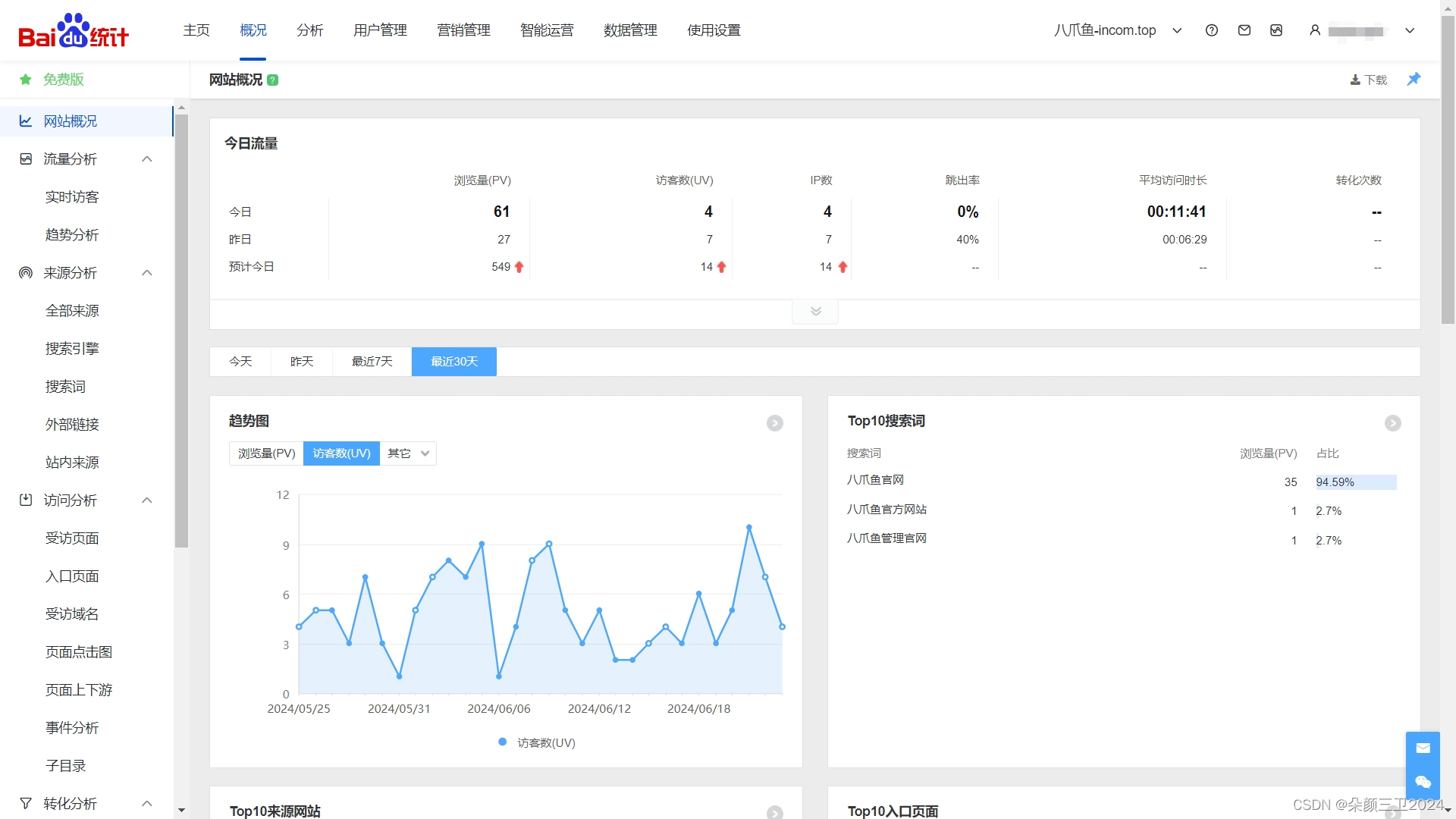
八爪鱼现金流-028,个人网站访问数据统计分析,解决方案
个人网站访问数据统计分析,解决方案 调研 结论:使用百度统计 步骤 1.注册百度统计 2.获取安装代码 3.在项目中,页面代码添加如下片段 <script>var _hmt _hmt || [];(function() {var hm document.createElement("script&…...

大厂面试官问我:布隆过滤器有不能扩容和删除的缺陷,有没有可以替代的数据结构呢?【后端八股文二:布隆过滤器八股文合集】
往期内容: 面试官问我:Redis处理点赞,如果瞬时涌入大量用户点赞(千万级),应当如何进行处理?【后端八股文(1)】-CSDN博客 本文为【布隆过滤器八股文合集】初版,…...

PHP米表域名出售管理源码带后台
源码介绍 html5米表源码PHP域名销售程序安装方法: 本站已测试,各项功能正常,功能易用,不复杂,非常适合个人米表使用 1、所有文件传至网站目录 2、浏览器执行http://你的访问网址/install 3、输入mysql帐号及密码信息,提交安装 源码截图 源码下载 …...
【开发12年码农教你】Android端简单易用的SPI框架-——-SPA
Service(priority 1) public class APrinterService implements IPrinterService { Override public void print() { System.out.println(“this is a printer service.”); } } 复制代码 B模块 —— BPrinterService Service(path“b_printer”, priority 2) public class…...
以太坊==MetaMask获取测试币最新网址
估算分数https://community.infura.io/t/unable-to-receive-sepolia-eth-from-faucet/7715 Gitcoin Passport 水龙头地址,填入自己的测试地址 水龙头项目地址 GitHub - pk910/PoWFaucet: Modularized faucet for EVM chains with different protection methods (…...

军用FPGA软件 Verilog语言的编码准测之触发器、锁存器
军用FPGA软件 Verilog语言的编码准测之触发器、锁存器 语言 :Verilg HDL EDA工具:ISE、Vivado、Quartus II 军用FPGA软件 Verilog语言的编码准测之触发器、锁存器一、引言二、基本编程规范之触发器强制准则1---禁止在同一个 always 语句中混合使用有复位…...
智能汽车 UI 风格独具魅力
智能汽车 UI 风格独具魅力...

javafx例子笔记
文章目录 创建过程javafx独立版报错 Exception in thread "WindowsNativeRunloopThread" java.lang.NoSuchMethodError: <init> javafx是java gui工具。 一般会转换为exe,成为可交互的应用。 那么来个简单的例子吧。 先说明一点,javafx不…...

【ajax基础】回调函数地狱
一:什么是回调函数地狱 在一个回调函数中嵌套另一个回调函数(甚至一直嵌套下去),形成回调函数地狱 回调函数地狱存在问题: 可读性差异常捕获严重耦合性严重 // 1. 获取默认第一个省份的名字axios({url: http://hmaj…...
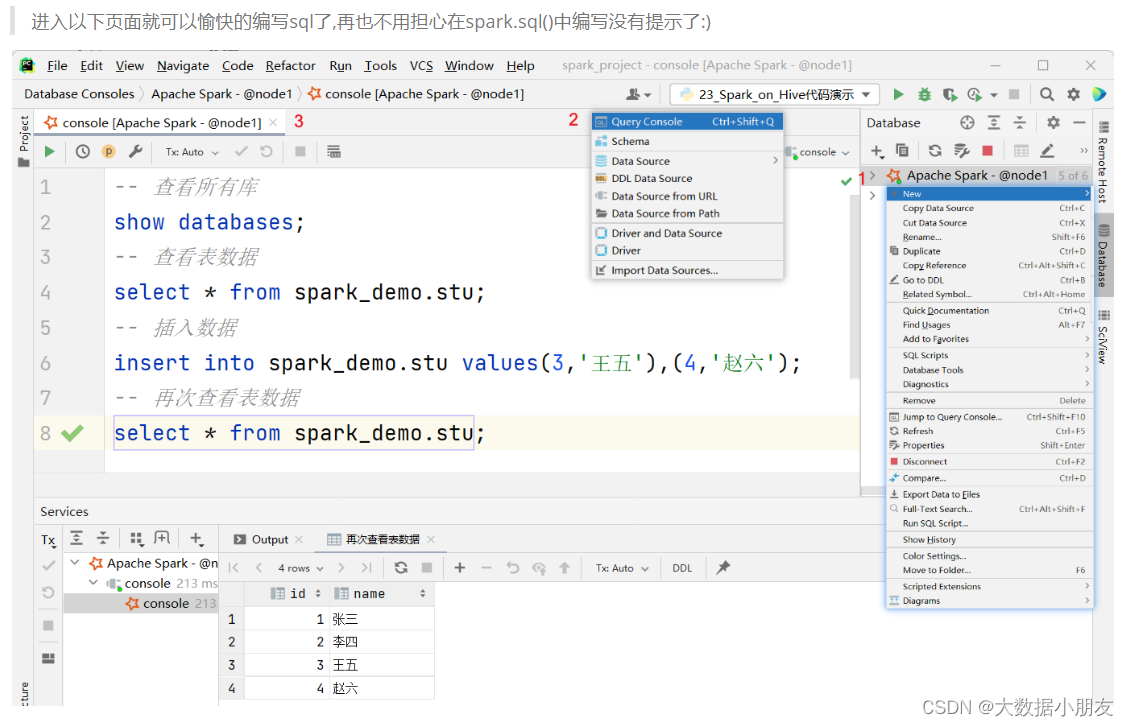
SparkSQL的分布式执行引擎-Thrift服务:学习总结(第七天)
系列文章目录 SparkSQL的分布式执行引擎 1、启动Thrift服务 2、beeline连接Thrift服务 3、开发工具连接Thrift服务 4、控制台编写SQL代码 文章目录 系列文章目录前言一、SparkSQL的分布式执行引擎(了解)1、启动Thrift服务2、beeline连接Thrift服务3、开发工具连接Thrift服务4、…...

联华集团:IT团队如何实现从成本中心提升至价值中心|OceanBase 《DB大咖说》(十)
OceanBase《DB大咖说》第 10 期,我们邀请到了联华集团的CTO楼杰,来分享他如何思考 IT 业务价值,以及联华华商数据库的升级实践。 楼杰从大学毕业后就进入了联华工作,并一直扎根在近 20 年的,从一名底层的技术员成长为…...
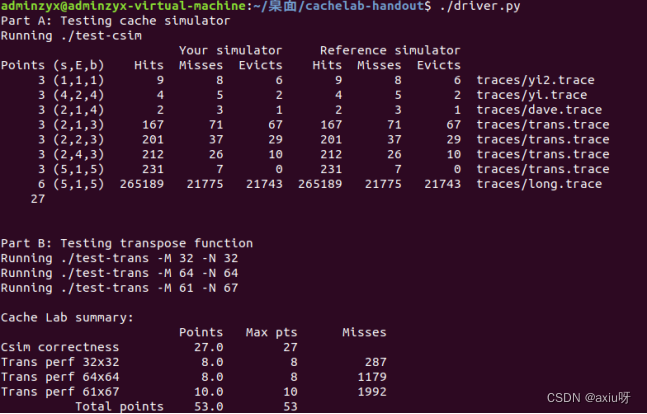
计算机系统基础实训五—CacheLab实验
实验目的与要求 1、让学生更好地应用程序性能的优化方法; 2、让学生更好地理解存储器层次结构在程序运行过程中所起的重要作用; 3、让学生更好地理解高速缓存对程序性能的影响; 实验原理与内容 本实验将帮助您了解缓存对C程序性能的影响…...

PHP框架之CodeIgniter框架
CodeIgniter框架详细说明 CodeIgniter是一个简单而强大的PHP框架,专为快速开发Web应用程序而设计。它遵循MVC(模型-视图-控制器)设计模式,为开发者提供了丰富的功能和灵活性,同时保持代码的轻量级和易于管理。CodeIgn…...
714. 买卖股票的最佳时机含手续费
714. 买卖股票的最佳时机含手续费 原题链接:完成情况:解题思路:ExplanationSummary 参考代码:_714买卖股票的最佳时机含手续费 错误经验吸取 原题链接: 714. 买卖股票的最佳时机含手续费 https://leetcode.cn/probl…...
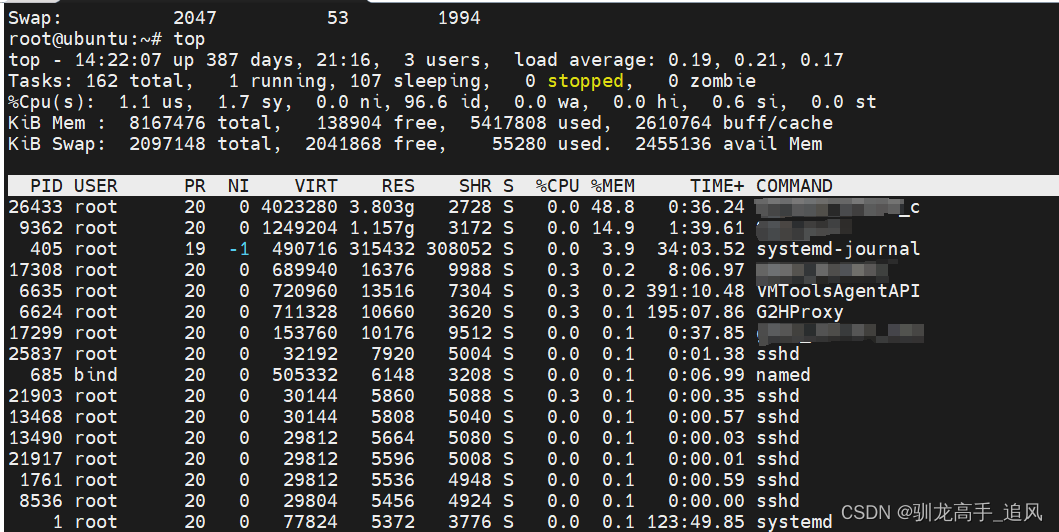
Linux系统查看程序内存及CPU占用
文章目录 1.free命令2.top命令3.PS命令3.1 查看内存占用前10位:3.2 查看CPU占用前10位 参考文档 1.free命令 可以通过free命令查看物理内存占用情况 #单位KB free #单位MB free -m #单位GB free -h 2.top命令 输入top命令,会输出定时刷新的程序PID、内…...
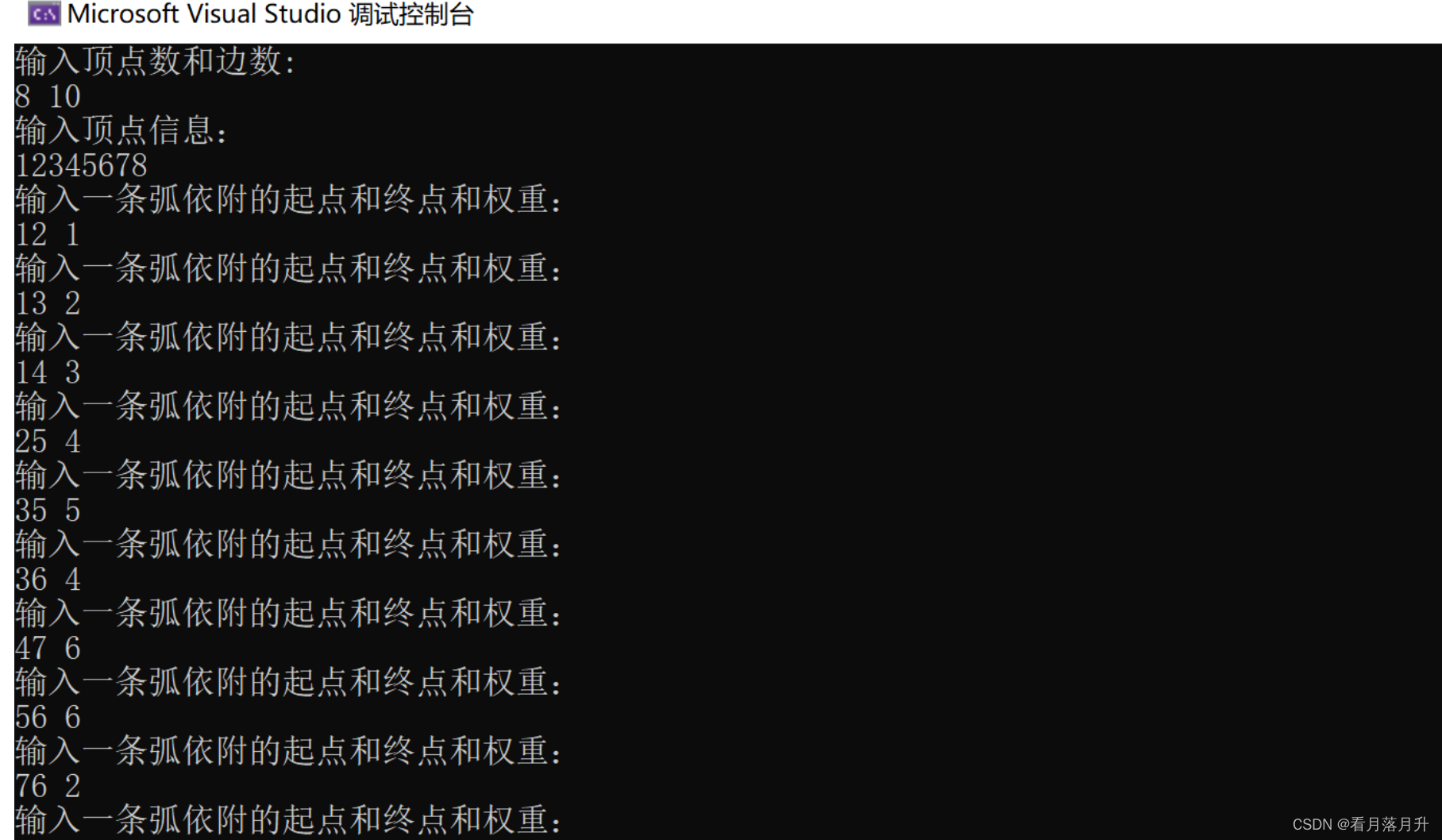
数据结构7---图
一、定义 对于图的定义,我们需要明确几个注意的地方:一线性表中我们把数据元素叫元素,树中叫结点,在途中数据元素我们则称之为顶点(Vertex)。 对于图的定义,我们需要明确几个注意的地方: 线性表中我们把数据元素叫元素…...
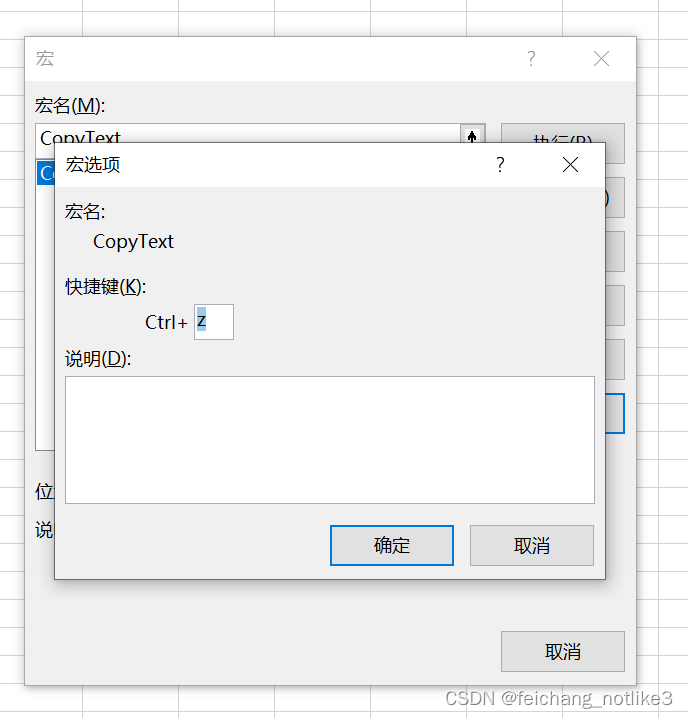
Excel 如何复制单元格而不换行
1. 打开excle, sheet1右键单击>查看代码>插入>模块 输入代码 Sub CopyText() Updated by NirmalDim xAutoWrapper As ObjectSet xAutoWrapper New DataObject or GetObject("New:{1C3B4210-F441-11CE-B9EA-00AA006B1A69}")xAutoWrapper.SetText ActiveC…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
