数据结构与算法笔记:基础篇 - 初始动态规划:如何巧妙解决“双十一”购物时的凑单问题?
概述
淘宝的 “双十一” 购物节有各种促销活动,比如 “满 200 元减 50元”。假设你女朋友购物车中有 n 个(n > 100)想买的商品,它希望从里面选几个,在凑够满减条件的前提下,让选出来的商品价格总和最长成都接近满减条件(200 元),这样就可以极大限度地 “薅羊毛”。作为程序员的你,能不能编个代码来帮她搞定?
要想高效地解决这个问题,就要用到本章讲的动态规划(Dynamic Programming)。
动态规划学习线路
动态规划比较适合用来求解最优问题,比如求最大值、最小值等等。它可以非常显著地降低时间复杂度,提高代码的执行效率。不过,它也是出了名的难学。它的主要学习难点跟递归类似,那就是求解问题的过程不太符合人类常规的思维方式。对于新手来说,想要入门确实不容易。不过,等你掌握了之后,你会发现,实际上并没有想象中那么难。
为了让你更容易理解动态规划,我分了三章进行讲解。这三章分别是,初始动态规划、动态规划理论、动态规划实战。
第一章,我会通过两个非常经典的动态规划问题模型,向你展示我们为什么需要动态规划,以及动态规划解题方法是如何演化出来的。实际上,你只要掌握了这两个例子的解决思路,对于其他很多动态规划问题,你都可以套用类似的思路来解决。
第二章,我会总结动态规划适合解决的问题的特征,以及动态规划解题思路。此外,还会将贪心、分治、回溯、动态规划这四种算法思想放在一起,对比分析它们各种的特点以及适用的场景。
第三章,我会教你应用第二节讲的动态规划理论知识,实战解决三个非常经典的动态规划问题,加深你对理论的理解。弄懂了这三章中的例子,对于动态规划这个知识点,你就算是入门了。
0-1 背包问题
再讲贪心算法、回溯算法时,多次讲到背包问题。本章,依旧拿这个问题来举例。
对于一组不同重量、不可分割的物品,我们需要选择一些装入背包,在满足背包最大重量限制的前提下,背包中物品总重量的最大值是多少?
关于这个问题,上篇文章讲了回溯的解决方法,也就是穷举搜索所有可能得装法,然后找出满足条件的最大值。不过,回溯算法的复杂度比较高,是指数级别。有没有什么规律,可以有效降低时间复杂度呢?我们一起来看看。
// 回溯算法实现private int maxW = Integer.MIN_VALUE; // 结果放到 maxW 中private int[] weight = {2,2,4,6,3}; // 物品重量private int n = 5; // 物品个数private int w = 9; // 背包承受的最大重量public void f(int i, int cw) { // 调用f(0,0)if (cw == w || i == n) { // cw == w表示装满了;i==n表示物品都考察完了if (cw > maxW) maxW = cw;return;}f(i+1, cw); // 选择不装第i个物品if (cw + weight[i] <= w) {f(i+1, cw + weight[i]); // 选择装第i个物品}}
规律是不是不好找?那我们就举个例子、画个图看看。我们假设背包的最大承重是 9。我们有 5 个不同的物品,每个物品的重量分别是 2,2,4,6,3。如果我们把这个例子的回溯求解过程,用递归树画出来,就是下面这个样子:
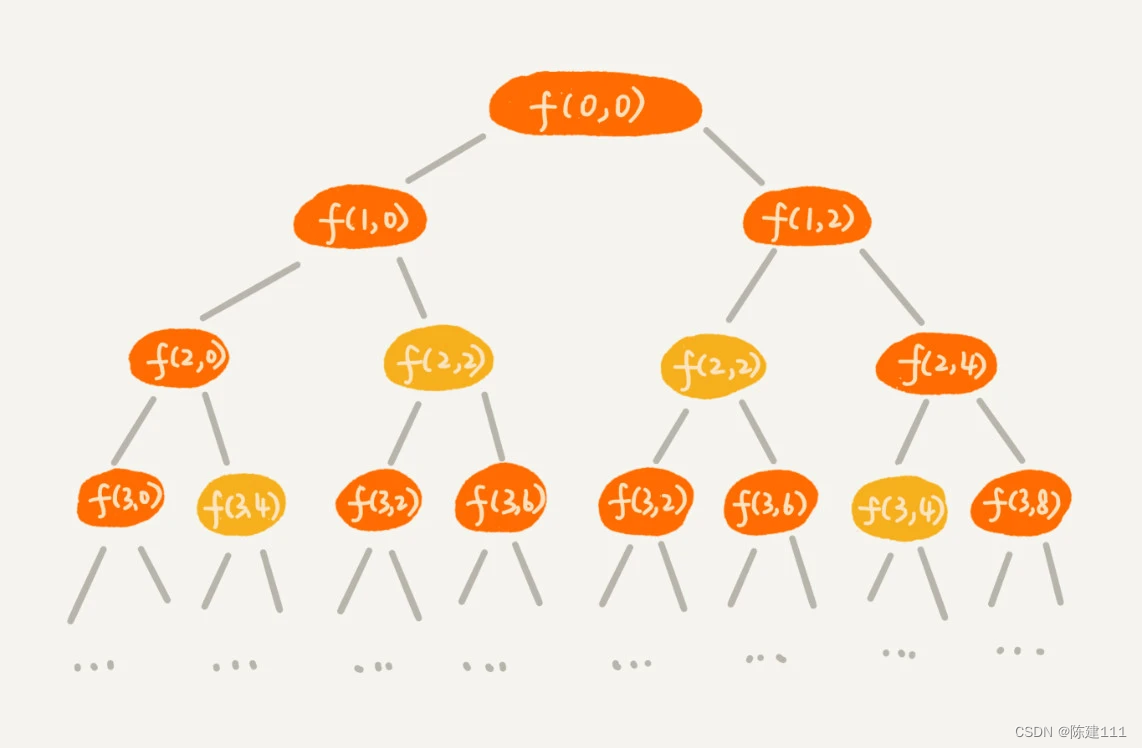
递归树种的每个结点表示一种状态,我们用 (i, cw) 来表示。其中,i 表示将要决策第几个物品是否装入背包,cw 表示当前背包中物品的总重量。比如,(2, 2) 表示我们将要决策第 2 个物品是否装入背包,在决策前,背包中的总总量是 2。
从递归树中,你应该会发现,有些子问题的求解是重复的,比如 f(2, 2) 和 f(3,4) 都被重复计算了两次。我们可以借助递归那一节将的 “备忘录” 的解决方式,记录已经计算好的 f(i,cw),当再次计算到重复的 f(i,cw) 时,可以直接从备忘录中取出来用,就不用再递归计算了,这样就可以比避免冗余计算。
// 回溯算法实现private int maxW = Integer.MIN_VALUE; // 结果放到 maxW 中private int[] weight = {2,2,4,6,3}; // 物品重量private int n = 5; // 物品个数private int w = 9; // 背包承受的最大重量private boolean[][] mem = new boolean[5][10]; //备忘录,默认为falsepublic void f(int i, int cw) { // 调用f(0,0)if (cw == w || i == n) { // cw == w表示装满了;i==n表示物品都考察完了if (cw > maxW) maxW = cw;return;}if (mem[i][cw]) return; // 重复状态mem[i][cw] = true;f(i+1, cw); // 选择不装第i个物品if (cw + weight[i] <= w) {f(i+1, cw + weight[i]); // 选择装第i个物品}}
这种解决方法非常好。实际上,它已经跟动态规划的执行效率基本上没有差别。但是,多一种方法就多一种解决思路,我们现在来看看动态规划是怎么做的。
我们把整个求解过程分为 n 个阶段,每个阶段会决策一个物品是否放到背包中。每个物品的决策(放入或不放入背包)完之后,背包中的重量会有多种情况,也就是说,会达到多种不同的状态,对应到递归树中,就是有很多不同的节点。
我们把每一层重复的状态(节点)合并,只记录不同的状态,然后基于上一层的状态集合,来推导下一层的状态集合。我们可以通过合并每一层的重复状态,这样就保证每一层不同状态的个数斗不过超过 w 个(w 表示背包的承载重量),也就是例子中的 9。于是,我们就成功避免了每层状态个数的指数级增长。
我们用一个二维数组 states[n][w+1],来记录每层可以达到的不同状态。
第 0 个(下标从 0 开始编号)物品的重量是 2,要么装入背包,要么不装入背包,决策完之后,会对应背包的两种状态,背包中物品的总重量是 0 或者 2。我们用 state[0][0]=true 和 state[0][2]=true 来表示这两种状态。
第 1 个物品的重量是 2,基于之前的背包状态,在这个物品决策完之后,不同的状态有 3 个,背包中物品总重量分别是 0(0+0),2(0+2 or 2+0),4(2+2)。我们用 state[1][0]=true, state[1][2]=true, state[1][4]=true 来表示这三种状态。
依次类推,直到考察完所有的物品后,整个 states 状态数组就计算好了。我把整个计算的过程画了出来,你可以看看。图中 0 表示 false,1 表示 true。我们只需要在最后一层,找一个职位 true 的最近接 w(这里是 9)的值,就是背包中物品总重量的最大值。
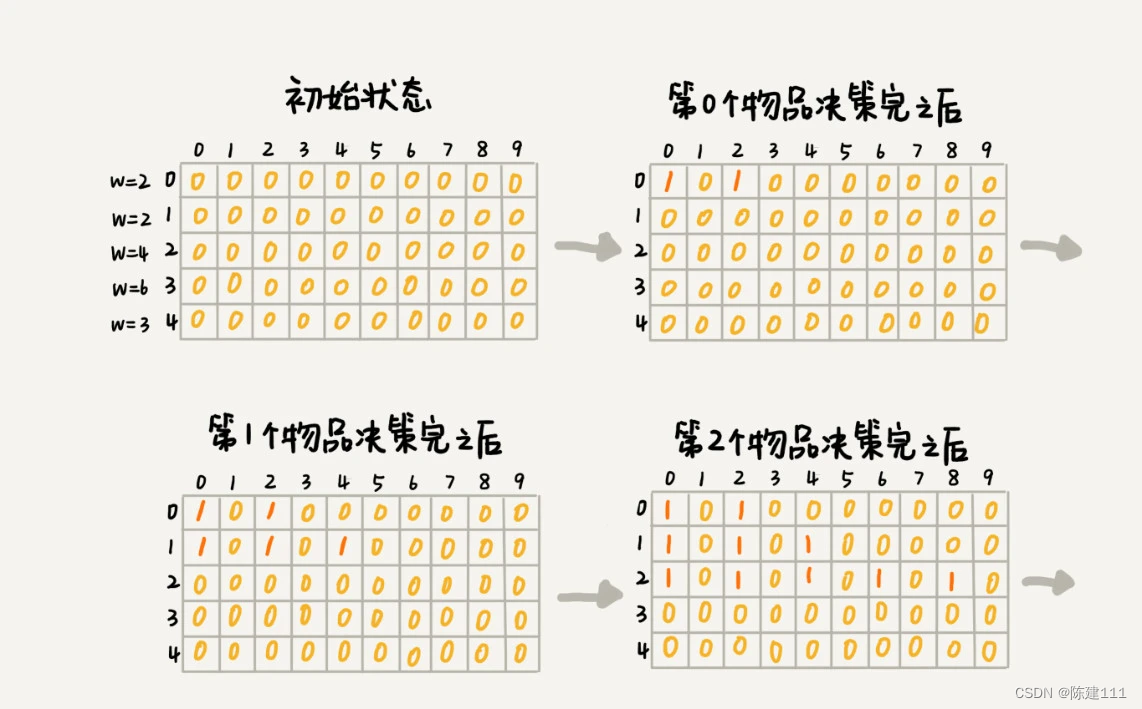
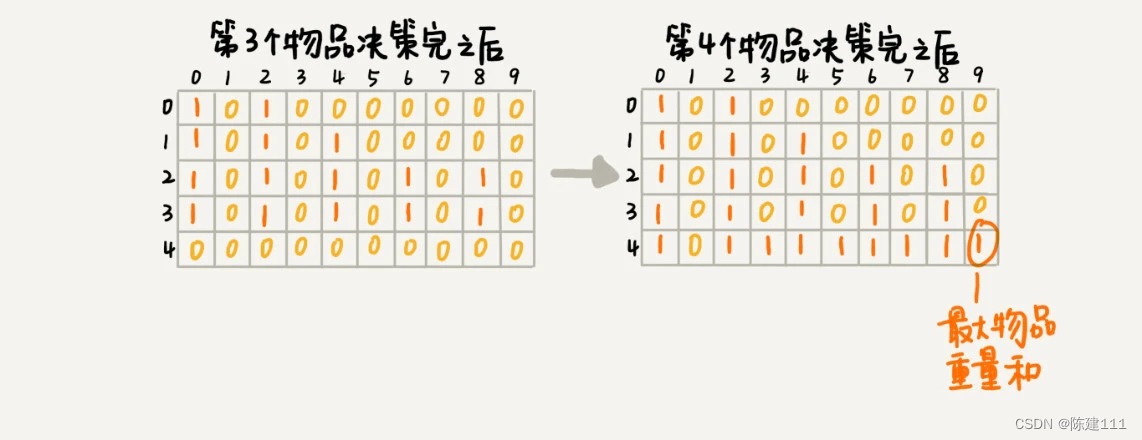
文字描述可能不够清楚。我把上面的过程,翻译成代码,你可以结合着一款看下。
// weight:物品重量,n:物品个数,w:背包重量public int knapsack(int[] weight, int n, int w) {boolean[][] states = new boolean[n][w+1]; // 默认值faslestates[0][0] = true; // 第一行的数据要特殊处理,可以利用哨兵优化if (weight[0] <= w) {states[0][weight[0]] = true;}for (int i = 1; i < n; i++) { // 动态规划状态转移for (int j = 0; j <= w; j++) { // 不把第i个物品放入背包if (states[i-1][j] == true) states[i][j] = true;}for (int j = 0; j <= w - weight[i]; j++) { // 把第i个物品放入背包if (states[i-1][j] == true) states[i][j+weight[i]] = true;}}for (int i = w; i >= 0; i--) { // 输出结果if (states[n-1][i] == true) return i;}return 0;}
实际上,这就是一种用动态规划解决问题的思路。我们把问题分解为多个阶段,每个阶段对应一个决策。我们记录每一个阶段可达的状态集合(去掉重复的),然后通过当前阶段的状态集合,来推导下一阶段的状态集合,动态地往前推进。这也是动态规划这个名字的由来,你可以自己体会一下,是不是还挺形象的?
前面我们讲到,用回溯算法解决这个问题的时间复杂度是 O ( 2 n ) O(2^n) O(2n),是指数级的。那动态规划解决方案的时间复杂度是多少呢?
这个代码的时间复杂度非常好分析,耗时最多的部分就是代码中的两层 for 循环,所以时间复杂度是 O ( n ∗ w ) O(n*w) O(n∗w)。n 表示物品个数,w 表示背包可以承受的总重量。
从理论上讲,指数级的时间复杂度肯定要比 O ( n ∗ w ) O(n*w) O(n∗w) 高很多。为了让你有更加深刻的感受,我来举个例子给你比较一下。
我们假设有 10000 个物品,重量分布在 1 到 15000 之间,背包可以承载的总重量是 30000。如果我们用回溯法解决,用具体的数值表示出时间复杂度是 2 10000 2^{10000} 210000,这是一个相当大的数字。如果我们用动态规划解决,用具体的数值表示出时间复杂度,就是 10000*30000。虽然看起来也很大,但是和 2 10000 2^{10000} 210000 比起来,要小太多。
尽管动态规划的执行效率比较高,但是就刚刚的代码来说,我们需要额外申请一个 n 乘以 m+1 的二维数组,对空间的消耗比较多。所以,有时候,我们会说,动态规划是一种空间换时间的解决思路。你可能要问了,有什么办法可以降低空间消耗吗?
实际上,我们只需要一个大小为 w+1 的一维数组就可以解决这个问题。动态规划状态转移的过程都可以基于一个一维数组来操作。具体的代码实现如下所示,你可以仔细看下。
public int knapsack2(int[] weight, int n, int w) {boolean[] states = new boolean[w+1]; // 默认值faslestates[0] = true; // 第一行的数据要特殊处理,可以利用哨兵优化if (weight[0] <= w) {states[weight[0]] = true;}for (int i = 1; i < n; i++) { // 动态规划状态转移// 不把第i个物品放入背包与i-1的结果一致,所以不用再处理for (int j = w - weight[i]; j >= 0; j--) { // 把第i个物品放入背包if (states[j] == true) states[j+weight[i]] = true;}}for (int j = w; j >= 0; j--) { // 输出结果if (states[j] == true) return j;}return 0;}
我强调一下代码中的第 9 行,j 需要从大到小来处理。如果我们按照 j 从小到大处理的话,会出现 for 循环重复计算的问题。
0-1 背包问题升级版
我们继续升级难度。我改造了一下刚刚的背包问题。你看下这个问题又该如何用动态规划解决呢?
刚刚讲的背包问题,只涉及背包重量和物品重量。我们现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品,我们选择将某些物品放入背包,在满足背包最大重量限制的前提下,背包中装入物品的总结之最大是多少呢?
这个问题依旧可以用回溯算法来解决。这个问题并不复杂,所以具体的实现思路,就不用文字描述了,直接给你看代码。
// 回溯算法实现private int maxV = Integer.MIN_VALUE; // 结果放到 maxW 中private int[] weight = {2,2,4,6,3}; // 物品重量private int[] value = {3,4,8,9,6}; // 物品价值private int n = 5; // 物品个数private int w = 9; // 背包承受的最大重量public void f(int i, int cw, int cv) { // 调用f(0,0,0)if (cw == w || i == n) { // cw == w表示装满了;i==n表示物品都考察完了if (cw > maxV) maxV = cw;return;}f(i+1, cw, cv); // 选择不装第i个物品if (cw + weight[i] <= w) {f(i+1, cw + weight[i], cv + value[i]); // 选择装第i个物品}}
针对上面的代码,我们还是照例画出递归树。在递归树中,每个节点表示一个状态。现在我们需要 3 个变量 (i,cw,cv) 来表示一个状态。其中,i 表示即将要决策的第 i 个物品是否装入背包,cw 表示当前背包中物品的总重量,cv 表示当前背包中物品的总价值。
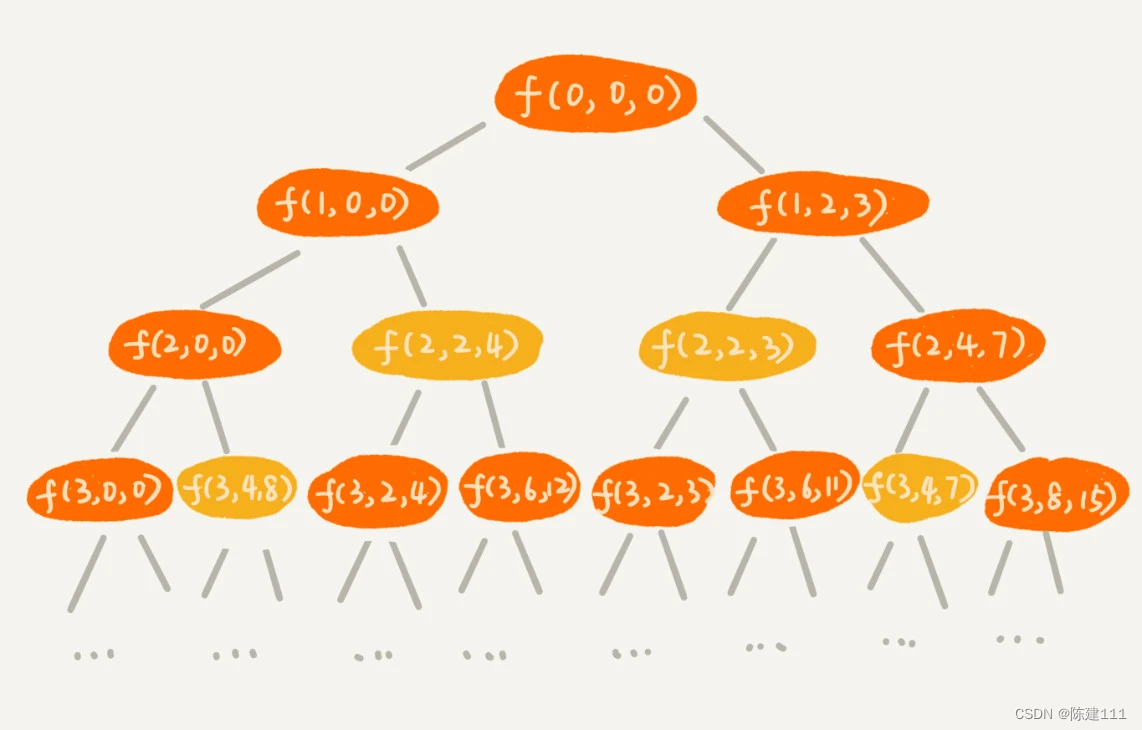
我们发现,在递归树中,有几个节点 i 和 cw 是相同的,比如 f(2,2,4) 和 f(2,2,3)。在背包中物品总重量是一样的情况下,f(2,2,4) 这种状态对应的物品总价值更大,我们可以舍弃 f(2,2,3) 这种状态,只需要沿着 f(2,2,4) 这条决策路线继续往下决策就可以。
也就是说,对于 (i,cw) 相同的不同状态,我们只需要保留 cv 值最大的那个,继续递归处理,其他状态不予考虑。
思路说完了,但是代码如何实现呢?如果用回溯算法,这个问题就没法再用 “备忘录” 解决了。所以,我们就需要换种思路,看看动态规划是不是更容易地解决这个问题?
我们还是把整个求解过程分为 n 个阶段,每个阶段会决策一个物品是否放到背包中。每个阶段决策完之后,背包中的物品的总重量以及总价值,会有多种情况,也就会达到多种不同的状态。
我们用一个二维数组 states[n][w+1],来记录每层可达到的不同状态。不过这里数组存储的值不再试 boolean,而是当前状态对应地最大总价值。我们把每一层中 (i,cw) 重复的状态(节点)合并,只记录 cv 值最大的那个状态,然后基于这些状态来推导下一层的状态。
我们把这个动态规划的过程翻译成代码,就是下面这个样子。
// weight:物品重量,value:物品价值,n:物品个数,w:背包重量public int knapsack3(int[] weight, int[] value, int n, int w) {int[][] states = new int[n][w+1];for (int i = 1; i < n; i++) { // 初始化statesfor (int j = 0; j <= w; j++) {states[i][j] = -1;}}states[0][0] = 0; // 第一行的数据要特殊处理,可以利用哨兵优化if (weight[0] <= w) {states[0][weight[0]] = value[0];}for (int i = 1; i < n; i++) { // 动态规划状态转移for (int j = 0; j <= w; j++) { // 不把第i个物品放入背包if (states[i-1][j] >= 0) states[i][j] = states[i-1][j];}for (int j = 0; j <= w - weight[i]; j++) { // 把第i个物品放入背包if (states[i-1][j] >= 0) {int v = states[i-1][j] + value[i];if (v > states[i][j + weight[i]]) {states[i][j + weight[i]] = v;}}}}// 找出最大值int maxValue = -1;for (int j = w; j >= 0; j--) { // 输出结果if (states[n-1][j] > maxValue) maxValue = states[n-1][j];}return maxValue;}
关于这个问题的时间、空间复杂度的分析,跟上一个例子大同小异,所以就不赘述了。我直接给出答案,时间复杂度是 O ( n ∗ w ) O(n*w) O(n∗w),空间复杂度也是 O ( n ∗ w ) O(n*w) O(n∗w)。跟上一个例子类似,空间复杂度也是可以优化的,你可以自己写一下。
如何巧妙解决“双十一”购物时的凑单问题?
对于这个问题,你当然可以利用回溯算法,穷举所有的排列组合,看大于等于 200 并且最接近 200 的组合是哪一个?但是,这样效率太低了点,时间复杂度非常高,是指数级的。当 n 很大时,可能 “双十一” 已经结束了,你的代码还没有运行处结果,这显然会让你在女朋友心中的形象大大减分。
实际上,它跟第一个例子中讲的 0-1 背包问题很像,只不过是把 “重量” 换成了价格。购物车中有 n 个商品。我们针对每个商品都决策是否否买。每次决策之后,对应不同的状态集合。我们还是用一个二维数组 states[n][x],来记录每次决策之后所有可达的状态。不过,这里的 x 值是多少呢?
0-1 背包问题中,我们找的是小于等于 w 的最大值,x 就是背包的最大承载重量 w+1。对于这个问题来说,我们要找的是大于等于 200(满减条件)的值中最小的,所以就不能设置 200 加 1了。就这个实际的问题而言,如果要购买的物品的总价格超过 200 太多,比如 1000,那这个羊毛 “薅” 得就没有太大意义了。所以,我们可以限定 x 值为 1001。
不过这个问题不仅要求大于等于 200 的总价格中的最小的,我们还要找出这个最小总价对应都该买哪些商品。实际上,我们可以利用 states 数组,倒推出这个被选择的商品序列。我先把代码写出来,待会再照着代码给你解释。
// items:商品价格;n:商品个数;w:满减条件,比如200public void double11advance(int[] items, int n, int w) {boolean[][] states = new boolean[n][3*w+1]; // 超过3被就没有薅羊毛的价值了states[0][0] = true; // 第一行的数据要特殊处理,可以利用哨兵优化if (items[0] <= 3*w) {states[0][items[0]] = true;}for (int i = 1; i < n; i++) { // 动态规划状态转移for (int j = 0; j < 3*w; j++) { // 不买第i个商品if (states[i-1][j] == true) states[i][j] = states[i-1][j];}for (int j = 3*w - items[i]; j >= 0; j--) { // 买第i个商品if (states[i-1][j] == true) states[i][j+items[i]] = true;}}int j;for (j = w; j < 3*w+1; j++) {if (states[n-1][j] == true) break; // 输出结果大于等于w的最小值}if (j == 3*w+1) return; // 没有可行解for (int i = n-1; i >= 0; i--) {if (j - items[i] >= 0 && states[i-1][j-items[i]] == true) {System.out.print(items[i] + " "); // 购买这个商品j = j - items[i];} // else 没有购买这个商品,j不变}if (j != 0) System.out.print(items[0]);}
代码的前半部分跟 0-1 背包问题没有什么不同,我们着重看下后半部分,看它是如何打印出选择购买哪些商品的。
状态 (i,j) 只有可能从 (i-1,j) 或者 (i-1, j-items[i]) 这两个状态推到过来。所以,我们就检查这两个状态是否是可达的,也就是 states[i-1][j] 或 states[i-1][j-items[i]] 是否为 true。
如果 states[i-1][j] 可达,就说明我们没有购买第 i 个上篇,如果 states[i-1][j-items[i]] 可达,那就说明我们选择购买了第 i 个商品。我们从中选择一个可达的状态(如果两个都可达,就随意选择一个),然后,继续迭代地考察其他商品是否有选择购买。
小结
动态规划的第一章到此就讲完了。内容比较多,你可能要多花一点时间来消化。
本章的内容不涉及动态规划的理论,我通过两个例子,给你展示了动态规划是如何解决问题的,并且一点一点详细给你讲解了动态规划解决问题的思路。这两个例子都是非常经典的动态规划问题,只要你真正搞懂了这两个问题,基本上动态规划就已经入门一半了。所以,你要多花点时间,真正弄懂这两个问题。
从例子中,你应该能发现,大部分动态规划能解决的问题,都可以通过回溯法来解决,只不过回溯算法解决起来比较低效,时间复杂度是指数级的。动态规划算法,在执行效率方面,要高很多。尽管执行效率提高了,但是动态规划的空间复杂度也提高了,所以,很多时候,我们会说,动态规划是一种空间换时间的算法思想。
前面也说了,本章的内容不涉及理论知识。这两个例子的分析过程,我并没有涉及任何高深的理论方面的东西。而且,我个人觉得,贪心、分治、回溯、动态规划,这四个算法有关的理论知识,大部分都是 “后验性” 的,也就是说,在解决问题的过程中,我们往往是先想到如何用某个算法思想解决问题,然后才用算法理论知识,去验证这个算法思想解决问题的正确性。所以,你大可不必过于急于寻求动态规划的理论知识。
相关文章:

数据结构与算法笔记:基础篇 - 初始动态规划:如何巧妙解决“双十一”购物时的凑单问题?
概述 淘宝的 “双十一” 购物节有各种促销活动,比如 “满 200 元减 50元”。假设你女朋友购物车中有 n 个(n > 100)想买的商品,它希望从里面选几个,在凑够满减条件的前提下,让选出来的商品价格总和最长…...

使用 select 进行 UART 通信的注意事项
文章目录 引言UART 通信中的 select 函数select 函数的工作原理使用 select 进行 UART 通信的注意事项示例代码 引言 UART(Universal Asynchronous Receiver/Transmitter)是一种用于异步串行通信的硬件协议,常用于计算机和外设之间的数据交换…...

干货 | 2024低空经济产业发展白皮书(免费下载)
【1】关注本公众号,转发当前文章到微信朋友圈 【2】私信发送 2024低空经济产业发展白皮书 【3】获取本方案PDF下载链接,直接下载即可。 如需下载本方案PPT/WORD原格式,诚挚邀请您微信扫描以下二维码加入方案驿站知识星球,获取上…...
打开nginx连接的php页面报错502
目录 问题描述: 原因: 1. 使用 Unix 域套接字(Unix Socket) 区别和优势: 2. 使用 TCP/IP 套接字 区别和优势: 如何选择 扩展:Rocky_Linux9.4安装PHP的步骤: 使用Remi存储库…...
)
Qt之文件操作(QFile、QFileInfo、QTemporaryFile)
文章目录 前言QFile如何使用 QFile QFileInfo如何使用 QFileInfo QTemporaryFile如何使用 QTemporaryFile QFile常用函数QFileInfo常用函数QTemporaryFile常用函数总结 前言 在开发 Qt 应用程序时,我们经常需要进行文件操作,如读取文件、写入文件、获取…...

Python爬虫初试
在Python中,我们可以使用一些强大的库来编写一个功能强大的爬虫, Python 首先安装必要的库(如果尚未安装) pip install requests beautifulsoup4 import requests from bs4 import BeautifulSoup import osdef download_images(…...
系统架构之系统初始化流程)
ARM-V9 RME(Realm Management Extension)系统架构之系统初始化流程
安全之安全(security)博客目录导读 目录 一、重置取消 二、应用处理单元(PE)初始启动 三、MSD初始化 四、GPT初始化 五、初始启动退出(由所有应用PE执行) 六、RMSD初始化 七、PE进入丢失上下文的低功耗状态 本博客提供了R…...
软件工程考试题备考
文章目录 前言一、二、1.2 总结 前言 一、 B D C 类图、对象图、包图 其他系统及用户 功能需求 用例 人、硬件或其他系统可以扮演的角色7. D C 数据 原型/系统原型;瀑布 A 功能;功能需求 D 数据存储;圆形/圆角矩形;矩形 C T;T;F C C B C D C …...
一款基于WordPress开发的高颜值的自适应主题Puock
主题特性 支持白天与暗黑模式 全局无刷新加载 支持博客与CMS布局 内置WP优化策略 一键全站变灰 网页压缩成一行 后台防恶意登录 内置出色的SEO功能 评论Ajax加载 文章点赞、打赏 支持Twemoji集成 支持QQ登录 丰富的广告位 丰富的小工具 自动百度链接提交 众多页面模板 支持评论…...

浙教版 七年级下册 科学复习干货
七年级下册 浙教版科学 复习干货 文章目录 七年级下册 浙教版科学 复习干货第 I 章人类 H u m a n Human Human人类生殖系统胚胎发育、娩出过程青春期 动物 A n i m a l Animal Animal生长时期有性生殖无性生殖 植物 P l a n t Plant Plant种子结构种子萌发芽花有性生殖无性…...

罗盘时钟lua迷你世界
--罗盘时钟 --星空露珠工作室制作 --作者:韩永旗 --数字换中文 local zhChar {一,二,三,四,五,六,七,八,九} function formatNumber( num ) if type(num)~number then return num..is not a num end if num>99 then return num..不是两位数 end if num0 then return 零 el…...

【Java】Java基础语法
一、注释详解 1.1 注释的语法: // 单行注释/*多行注释 *//**文档注释 */ 1.2 注释的特点: 注释不影响程序的执行,在Javac命令进行编译后会将注释去掉 1.3 注释的快捷键 二、字面量详解 2.1 字面量的概念: 计算机是用来处理…...
利用golang_Consul代码实现Prometheus监控目标的注册以及动态发现与配置
文章目录 前言一、prometheus发现方式二、监控指标注册架构图三、部分代码展示1.核心思想2.代码目录3、程序入口函数剖析4、settings配置文件5、初始化配置文件及consul6、全局变量7、配置config8、公共方法目录common9、工具目录tools10、service层展示11、命令行参数12、Make…...
Python爬虫介绍
Python 作为一种广泛应用的编程语言,在 Web 开发、大数据开发、人工智能开发和嵌入式开发等领域都有着重要的应用。 Python 的易学性、清晰性和可移植性等特点使它得到很多技术人士的喜爱。对于数据科学和机器学习领域的程序员来说,Python 提供了强大的…...
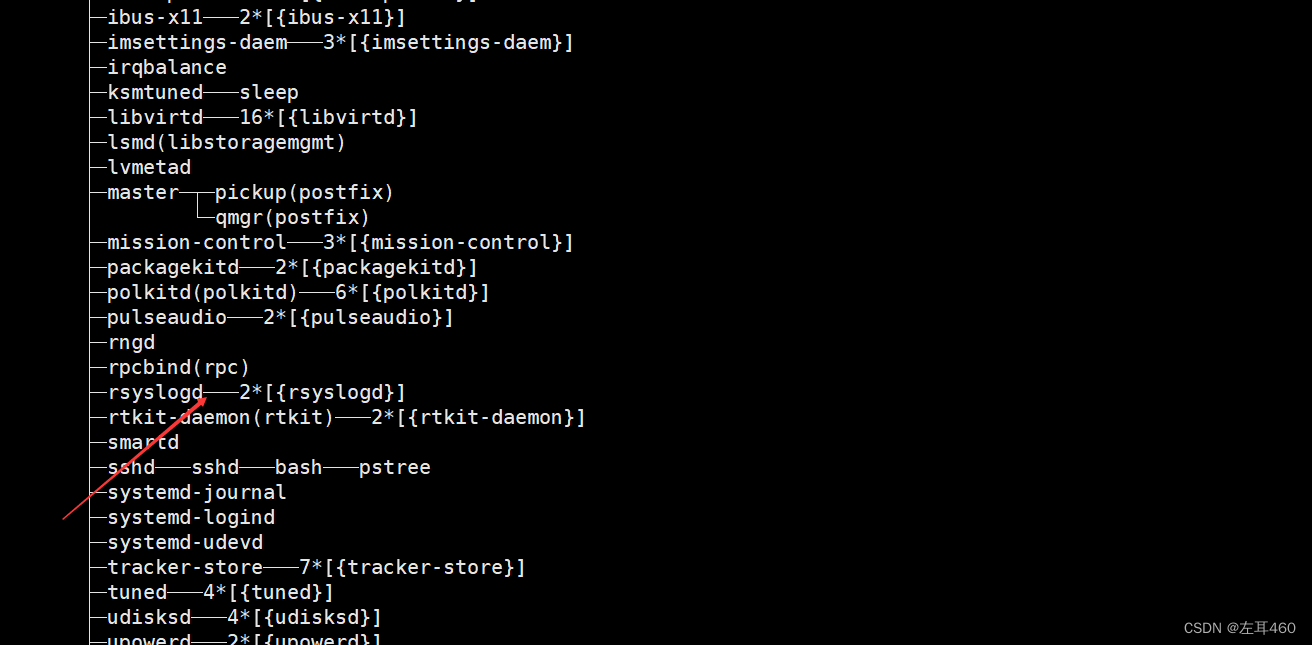
Linux 进程管理
一、查看进程 使用ps -aux进行查看,其中a表示列出所有进程信息,u以用户格式显示进程信息,x显示后台进程参数,也可以使用| grep 进行进程的筛选 以下是显示进程后的示意 USER为进程执行的用户 PID为进程号 %CPU为该进程的cpu占用…...

【车载测试】CAN协议、CAN- FD协议和FlexRay协议 区别
【上半场电动化,下半场智能化】 一、CAN协议 和 CAN- FD协议的区别 CAN(Controller Area Network)协议是一种广泛用于汽车和工业控制系统等领域的现场总线协议。CAN- FD(Flexible Data Rate)协议是对CAN协议的扩展&am…...

对日期的处理
对日期的处理 对编码进行统一,在脚本最开始: # -*- coding: utf-8 -*-这里涉及到两个操作,一个是将数据进行标准化,比如有些日期是2024/05/06这并不符合日期的标准格式,需要转换成这样的2024-05-06 def tran_std(st…...

赵丽颖纯白茉莉绽放温柔之美
赵丽颖纯白茉莉,绽放温柔之美在这个繁忙喧嚣的娱乐圈,赵丽颖以其独特的魅力,成为了无数人心中的白月光。近日,赵丽颖工作室发布了一组live图,她身着一袭温柔白裙,宛如一朵盛开的纯白茉莉花,美得…...

软考高级论文真题“论湖仓一体架构及其应用”
论文真题 随着5G、大数据、人工智能、物联网等技术的不断成熟,各行各业的业务场景日益复杂,企业数据呈现出大规模、多样性的特点,特别是非结构化数据呈现出爆发式增长趋势。在这一背景下,企业数据管理不再局限于传统的结构化OLTP…...

CentOS系统查看版本的各个命令
cat /etc/centos-release 查看CentOS版本 uname -a 命令的结果分别代表:当前系统的内核名称、主机名、内核发型版本、节点名、系统时间、硬件名称、硬件平台、处理器类型以及操作系统名称 cat /proc/version 命令用于查看Linux内核的版本信息。执行该命令后…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
