密码学及其应用——为什么选择接近的质数因子对RSA加密算法不安全?
RSA加密算法是一种广泛使用的非对称加密算法,它的安全性依赖于大整数分解的难度。具体来说,RSA算法生成的公钥包含一个大整数N,这是两个大质数p和q的乘积。然而,如果这两个质数p和q太接近,则可以相对容易地对N进行因式分解,从而破解加密。
1. 质数选择的影响
在RSA加密算法中,选择的质数p和q不应过于接近。如果p和q的差距很小,那么可以通过以下方法进行因式分解:
1.1 计算 的值
的值
假设且
(假设
)。根据代数恒等式,我们有:
进一步展开和简化,可以得到:
1.2 利用这个结果来分解N
由于,我们可以通过找到满足这个等式的t和s来尝试分解N。如果能够找到这样的t和s,那么可以利用t和s来计算p和q。具体来说,p和q可以通过解二元一次方程组
和
来找到。
2. 实际例子
让我们来看一个具体的例子,通过代码实现上述方法来分解给定的。
import mathdef fermat_factor(n):a = math.isqrt(n)b2 = a * a - nb = math.isqrt(b2)while b * b != b2:a += 1b2 = a * a - nb = math.isqrt(b2)p = a + bq = a - breturn p, qN = 1607363
p, q = fermat_factor(N)
print(f"p = {p}, q = {q}")
运行上述代码后,我们可以得到p和q的值:
p = 1439, q = 1117这个例子清楚地展示了为什么在RSA中选择接近的质数因子是不安全的。通过利用p和q过于接近的弱点,我们可以成功分解N并找到质数因子,从而破解RSA加密。
3. 总结
为了保证RSA加密算法的安全性,质数因子p和q需要选择得足够远离。这不仅增加了因式分解的难度,还确保了加密系统的安全性。上述例子展示了如果质数因子选择不当,攻击者可以通过相对简单的数学方法轻松破解RSA加密。这强调了在密码学中,细节和选择的正确性对安全性的重要性。
相关文章:
密码学及其应用——为什么选择接近的质数因子对RSA加密算法不安全?
RSA加密算法是一种广泛使用的非对称加密算法,它的安全性依赖于大整数分解的难度。具体来说,RSA算法生成的公钥包含一个大整数N,这是两个大质数p和q的乘积。然而,如果这两个质数p和q太接近,则可以相对容易地对N进行因式…...

爱心商城管理系统的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,企业管理,用户管理,论坛管理,商品管理,公告管理,用户捐赠 企业账户功能包括:系统首页,个人中…...

【python】linux下安装chromedriver
首先,安装selenium模块 pip3 install selenium查看系统内chrome版本: google-chrome --version 根据谷歌浏览器版本下载对应的浏览器驱动版本: wget https://storage.googleapis.com/chrome-for-testing-public/126.0.6478.114/linux64/ch…...

Day18—使用Scrapy框架快速开发爬虫
Scrapy是一个强大的Python框架,用于快速开发爬虫程序。它提供了一整套工具来处理网页爬取和数据提取,非常适合于数据挖掘和信息抓取。本文将详细介绍如何使用Scrapy框架,包括创建项目、编写爬虫规则、设置中间件和管道等。 1. Scrapy框架概述 Scrapy框架以其高性能、易用性…...
04--MySQL8.0_JDBC
第一章 JDBC概述 之前我们学习了JavaSE,编写了Java程序,数据保存在变量、数组、集合等中,无法持久化,后来学习了IO流可以将数据写入文件,但不方便管理数据以及维护数据的关系; 后来我们学习了数据库管理软件MySQL,可以方便的管理数据1。 那么如何将它俩结合起来呢?即…...
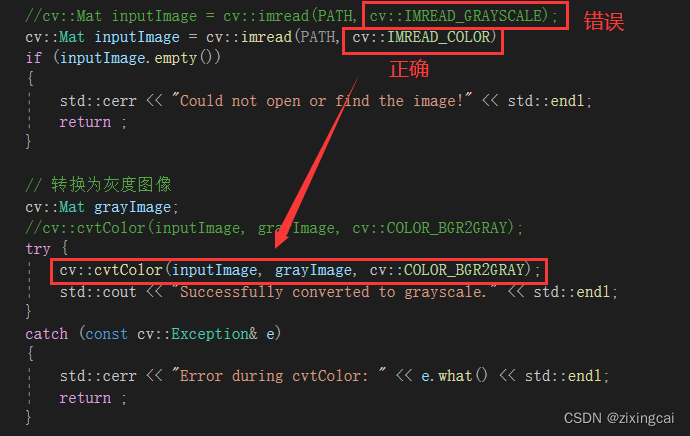
OPENCV中0x00007FFE5F35F39C发生异常
原因:读取图片时已经为灰度图像,又进行了一次灰度处理cvtColor 解决方法:如上图所示,将cv::imread的第二个参数改为cv::IMREAD_COLOR;或者保留cv::IMREAD_GRAYSCALE,删去后面的cv::cvtColor...
 -- 第三部分(行为型模式))
Python 设计模式(第2版) -- 第三部分(行为型模式)
Python 设计模式(第2版) 再介绍下行为型设计模式。 行为型模式,顾名思义,它主要关注的是对象的责任。它们用来处理对象之间的交互,以实现更大的功能。行为型模式建议:对象之间应该能够彼此交互,同时还应该是松散耦合…...
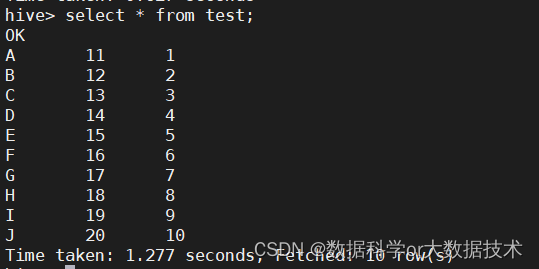
EXCEL数据导入HIVE
引言 本文将论述如何将Windows本地的excel表数据,导入到虚拟机Linux系统中的Hadoop生态中的Hive数据仓库中。 实验准备 DBeaver Hive3.1(Hadoop3.1) excel数据表 实验步骤 一、首先打开虚拟机,启动Hadoop,启动h…...

C语言常用标准头文件
头文件的基础概念 在C的系列语言程序中,头文件(通常扩展名为.h)被大量使用,它通常包含函数、变量、结构体等的声明和定义,以及一些宏定义和类型定义。头文件的主要作用是为了方便管理和重用代码,它可以被多…...
vuejs3用gsap实现动画
效果 gsap官网地址: https://gsap.com/ 安装gsap npm i gsap 创建Gsap.vue文件 <script setup> import {reactive, watch} from "vue"; import gsap from "gsap"; const props defineProps({value:{type:Number,default:0} }) cons…...

企业级-PDF文件下载
作者:fyupeng 技术专栏:☞ https://github.com/fyupeng 项目地址:☞ https://github.com/fyupeng/rpc-netty-framework 留给读者 一、介绍 文件下载在浏览器可以根据响应头设置纯下载和直接打开两种方式。 二、代码 RequestMapping("/…...

00 - React 基础
1. React 基础 安装react指令 可参考: 官网官网使用教程 如: npx create-react-app 项目名 如:npx create-react-app react-redux-proJSX JSX 是一种 JavaScript 的语法扩展,类似于 XML 或 HTML,允许我们在 Java…...

基于WPF技术的换热站智能监控系统17--项目总结
1、项目颜值,你打几分? 基于WPF技术的换热站智能监控系统01--项目创建-CSDN博客 基于WPF技术的换热站智能监控系统02--标题栏实现-CSDN博客 基于WPF技术的换热站智能监控系统03--实现左侧加载动画_wpf控制系统-CSDN博客 基于WPF技术的换热站智能监…...

CI /CD学习
CI/CD概述 CI/CD 是持续集成和持续交付/部署的缩写,旨在简化并加快软件开发生命周期。 持续集成(CI)是指自动且频繁地将代码更改集成到共享源代码存储库中的做法。持续交付和/或持续部署(CD)是一个由两部分组成的过程…...
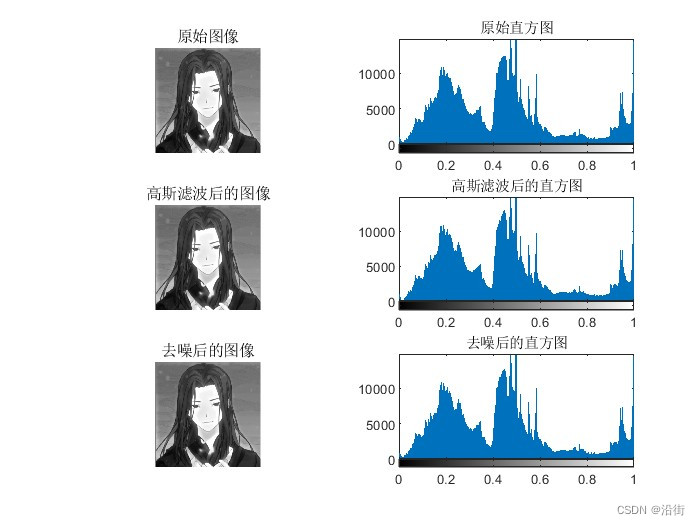
基于matlab的高斯滤波与图像去噪
1 高斯滤波原理 1.1 原理 高斯滤波是一种线性平滑滤波技术,主要用于消除图像中的高斯噪声。它的工作原理可以理解为对整幅图像进行加权平均的过程,即每个像素点的值都由其本身和邻域内的其他像素值经过加权平均后得到。 高斯滤波实质上是一种信号的滤…...
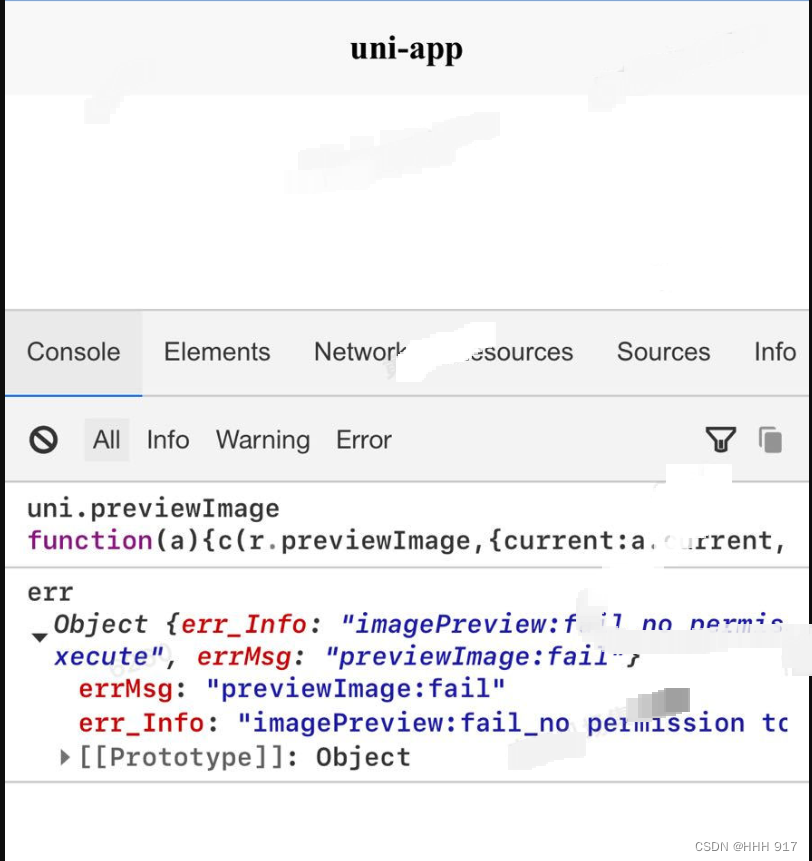
解决 uniapp h5 页面在私有企微iOS平台 间歇性调用uni api不成功问题(uni.previewImage为例)。
demo <template><view class"content"><image class"logo" src"/static/logo.png"></image><button click"previewImage">预览图片</button></view> </template><script> //打…...
Jenkins nginx自动化构建前端vue项目
在现代的Web开发中,Vue.js已经成为一种非常流行的JavaScript框架。为了更高效地管理和部署Vue.js项目,使用自动化构建工具是至关重要的。Jenkins作为一款强大的持续集成和持续部署(CI/CD)工具,为我们提供了一种便捷的方…...

Devicetree - 删除某个节点或属性
在设备树(devicetree)中,删除语法用于从现有设备树中删除属性或节点。这通常在设备树覆盖文件(DTS)或片段文件中完成。该语法使用 /delete-property/ 和 /delete-node/ 指令。 以下是如何使用这些指令的示例࿱…...

Xcode will continue when the operation completes
Xcode 15后,连接手机经常出现 Preparing iPhone. Xcode will continue when the operation completes.记录一下解决办法。其他提示,Xcode连接不上手机也可以尝试通过这个方法解决。 注意:最好关闭科学上网再操作。 从Xcode取消iPhone的配对(右键单击 -Unpair Devi…...
Python爬虫-贝壳新房
前言 本文是该专栏的第32篇,后面会持续分享python爬虫干货知识,记得关注。 本文以某房网为例,如下图所示,采集对应城市的新房房源数据。具体实现思路和详细逻辑,笔者将在正文结合完整代码进行详细介绍。接下来,跟着笔者直接往下看正文详细内容。(附带完整代码) 正文 地…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
