代码随想录算法训练营day64 | 98. 所有可达路径
图论理论基础
1、图的种类
整体上一般分为 有向图 和 无向图。
加权有向图,就是图中边是有权值的,加权无向图也是同理。
2、度
无向图中有几条边连接该节点,该节点就有几度
在有向图中,每个节点有出度和入度。出度:从该节点出发的边的个数。入度:指向该节点边的个数。
3、连通性
在图中表示节点的连通情况,我们称之为连通性
连通图和强连通图
- 在无向图中,任何两个节点都是可以到达的,我们称之为连通图。如果有节点不能到达其他节点,则为非连通图。
- 在有向图中,任何两个节点是可以相互到达的,我们称之为 强连通图。
连通分量和强连通分量
- 在无向图中的极大连通子图称之为该图的一个连通分量。
- 在有向图中极大强连通子图称之为该图的强连通分量。
4、图的构造
一般使用邻接表、邻接矩阵 或者用类来表示。主要是 朴素存储、邻接表和邻接矩阵。
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
邻接矩阵
优点:
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
缺点:
- 遇到稀疏图,会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
- 邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
邻接表
优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点连接情况相对容易
缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点连接其他节点的数量。
- 实现相对复杂,不易理解
5、图的遍历方式
- 深度优先搜索(dfs)
- 广度优先搜索(bfs)
深搜理论基础
关键就两点:
- 搜索方向,是认准一个方向搜,直到碰壁之后再换方向
- 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程
代码框架
void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}98. 所有可达路径(卡码网)
深搜三部曲
- 确认递归函数,参数
- 确认终止条件
- 处理目前搜索节点出发的路径
邻接矩阵写法
def dfs(graph, x, n, result, path):# 当前遍历的节点x 到达节点n if x == n: # 找到符合条件的一条路径result.append(path[:])returnfor i in range(1, n+1): # 遍历节点x链接的所有节点if graph[x][i] == 1: path.append(i)dfs(graph, i, n, result, path)path.pop()if __name__ == "__main__":n, m = map(int, input().strip().split())# 节点编号从1到n,所以申请 n+1 这么大的数组graph = [[0] * (n + 1) for _ in range(n+1)]for _ in range(m):s, t = map(int, input().strip().split())# 使用邻接矩阵 表示无线图,1 表示 s 与 t 是相连的graph[s][t] = 1result = []dfs(graph, 1, n, result, [1])# 输出结果if len(result) == 0:print(-1)for path in result:print(" ".join([str(i) for i in path]))
邻接表写法
def dfs(graph, x, n, result, path):# 当前遍历的节点x 到达节点n if x == n: # 找到符合条件的一条路径result.append(path[:])returnfor i in graph[x]: # 遍历节点x链接的所有节点path.append(i)dfs(graph, i, n, result, path)path.pop()if __name__ == "__main__":n, m = map(int, input().strip().split())# 节点编号从1到n,所以申请 n+1 这么大的数组graph = [[] for _ in range(n+1)] # 邻接表for _ in range(m):s, t = map(int, input().strip().split())# 使用邻接表graph[s].append(t)result = []dfs(graph, 1, n, result, [1])# 输出结果if len(result) == 0:print(-1)for path in result:print(" ".join([str(i) for i in path]))主要在生成图和遍历图的时候不一样
广搜理论基础
广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
代码框架
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图,也就是一个二维数组
// visited标记访问过的节点,不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列que.push({x, y}); // 起始节点加入队列visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点while(!que.empty()) { // 开始遍历队列里的元素pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + dir[i][0];int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过if (!visited[nextx][nexty]) { // 如果节点没被访问过que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问}}}}相关文章:

代码随想录算法训练营day64 | 98. 所有可达路径
图论理论基础 1、图的种类 整体上一般分为 有向图 和 无向图。 加权有向图,就是图中边是有权值的,加权无向图也是同理。 2、度 无向图中有几条边连接该节点,该节点就有几度 在有向图中,每个节点有出度和入度。出度ÿ…...
php上传zip压缩包到服务器并解压,解析压缩包内excel表格数据导入到数据库
需求: 1.需要管理后台将excel表格中的每条单词数据导入到数据库中. 2.每条单词数据对应的图片和音频文件需要上传到服务器中. 为了让客户上传数据方便,考虑了一下决定通过后台上传压缩包的方式实现 测试压缩包: 压缩包的目录结构 管理后台导入教材 public function upload…...

48-5 内网渗透 - JuicyPotato、Pipe Potato提权
Juicy Potato Juicy Potato 与 Rotten Potato(烂土豆) 的原理几乎完全相同,只是在后者的基础上做了扩展,以便更灵活地利用 Rotten Potato。Juicy Potato 不再像 Rotten Potato 那样依赖于一个现有的 Meterpreter,并且可以自定义 COM 对象加载的端口,以及根据系统版本更换…...
Windows C++ 应用软件开发从入门到精通详解
目录 1、引言 2、IDE 开发环境介绍 2.1、Visual Studio 2.2、Qt Creator 3、 C语言特性 3.1、熟悉泛型编程 3.2、了解C/C异常处理 3.3、熟练使用STL容器 3.4、熟悉C11新特性 4、Windows 平台的编程技术与调试技能 4.1、需要掌握的若干编程技术和基础知识 4.2、需…...

Leetcode 3195. Find the Minimum Area to Cover All Ones I
Leetcode 3195. Find the Minimum Area to Cover All Ones I 1. 解题思路2. 代码实现 题目链接:3195. Find the Minimum Area to Cover All Ones I 1. 解题思路 这一题还是挺简单的,只要找到所有1所在的元素的上下左右4个边界,作为目标矩形…...

ONLYOFFICE8.1版本桌面编辑器测评
目录 一、引言 二、界面设计:简洁大方,操作便捷 三、功能评测:全面升级,满足多样需求 四、性能评测:稳定流畅,高效运行 五、总结与展望 ONLYOFFICE官网链接:ONLYOFFICE - 企业在线办公应用…...

线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
文章目录 1. 单位矩阵的秩1变换1.1 功能说明1.2 证明 2. 单位矩阵 I n I_n In的秩k变换3. 一般矩阵A的秩k变换4. 公式用途4.1 求解方程4.2 卡曼滤波 1. 单位矩阵的秩1变换 1.1 功能说明 假设我们有一个单位矩阵I,列向量u,v那么当我们对单位向量I减去秩为1的矩阵…...

强强联合 极光推送(JPush)成为华为生态市场首家推送类SDK服务商
近日,中国领先的客户互动和营销科技服务商,极光(Aurora Mobile,纳斯达克股票代码:JG)的核心产品极光推送(JPush)顺利通过华为开发者联盟的多项测试及审核,成为首家在Harm…...

防止在 Qt 中触发信号
在 Qt 中工作时,有时我们需要暂时阻止某些信号的触发。以下是一个经典场景:我们有一个 QCheckBox 对象,当用户勾选或取消勾选时,需要调用一个函数,因此我们将这个函数连接到 stateChanged(int state) 信号。然而&#…...
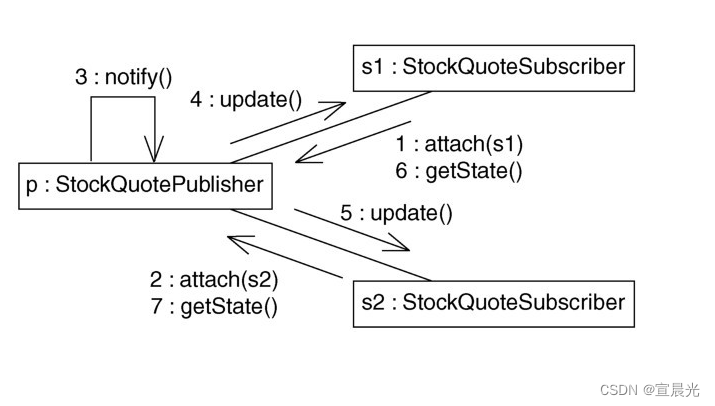
【UML用户指南】-17-对基本行为建模-交互
目录 1、消息的可视化表示 2、对象与角色 3、链和连接件 4、消息 5、序列 6、创建、修改和撤销 7、表示法 8、常用建模技术 8.1、对控制流建模 8.1.1、基于时间的控制流 8.1.2、基于结构的控制流 在任何有意义的系统中,对象都不是孤立存在的,…...

Java中的类加载器与热部署技术详解
Java中的类加载器与热部署技术详解 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在软件开发中,特别是在大型应用和服务的开发过程中,类…...
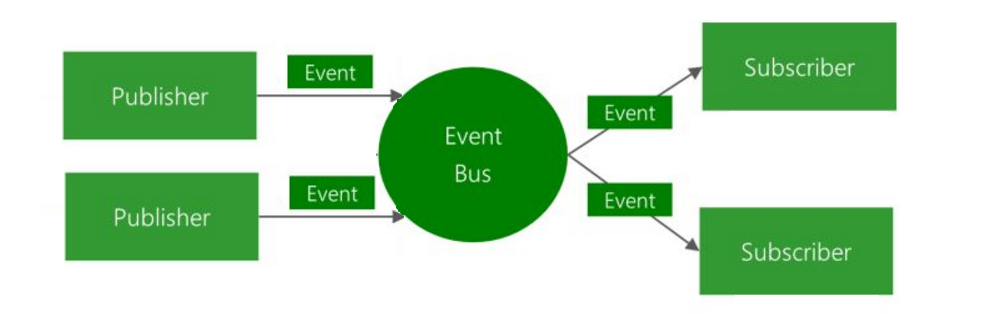
【事件总线】EventBus
文章目录 概述如何使用如何发布消息如何进行消息监听 来源 概述 事件总线是对发布-订阅模式(观察者)的一种实现,是一种集中式事件处理机制,允许不同的组件之间进行彼此通信而又不需要相互依赖,达到一种解耦的目的。 …...
LeetCode 热题100 --双指针
双指针 b站UP主蜜糖:由于数据特征的有序性(大小或者正负),所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。 283.移动零 相关标签 :…...

从《深入设计模式》一书中学到的编程智慧
软件设计原则 优秀设计的特征 在开始学习实际的模式前,让我们来看看软件架构的设计过程,了解一下需要达成目标与需要尽量避免的陷阱。 代码复用 无论是开发何种软件产品,成本和时间都最重要的两个维度。较短的开发时间意味着可比竞争对…...

Redis 基本配置
Redis的配置文件通常位于 /etc/redis/redis.conf。以下是一些常见的Redis配置选项和它们的说明: 基本配置 1. 绑定地址 bind 127.0.0.1默认情况下,Redis只监听本地接口。如果需要远程访问,可以修改成bind 0.0.0.0,不过这会带来…...
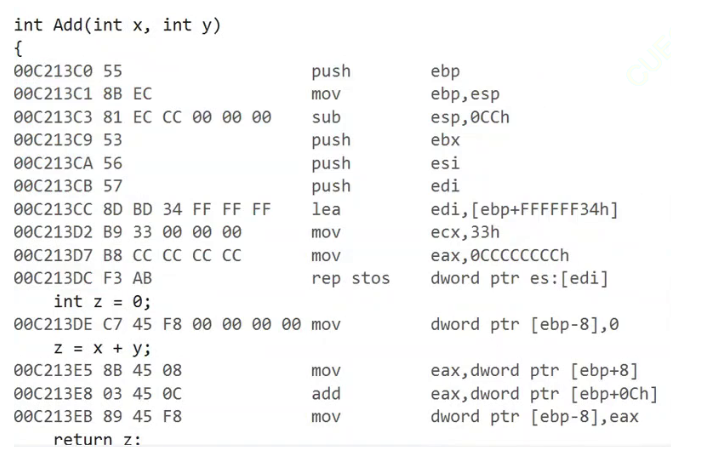
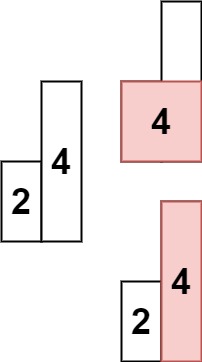
【C++庖丁解牛】函数栈帧的创建与销毁
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1. 寄存器2. ebp和esp是如…...
Java基础16(集合框架 List ArrayList容器类 ArrayList底层源码解析及扩容机制)
目录 一、什么是集合? 二、集合接口 三、List集合 四、ArrayList容器类 1. 常用方法 1.1 增加 1.2 查找 int size() E get(int index) int indexOf(Object c) boolean contains(Object c) boolean isEmpty() List SubList(int fromindex,int …...

数组:移除元素
参考资料:代码随想录 本题思路:通过快慢指针将两次循环减少到一次 class Solution {public int removeElement(int[] nums, int val) {//0 1 2 2 2 2 3int fast 0;int slow 0;while(fast < nums.length){if(nums[fast] ! val){nums[slow] nums[f…...
——通信杂谈(完结))
胡说八道(24.6.22)——通信杂谈(完结)
上回书说到雷达和香农的信息论,今天来进行完结。 数字幅值调制或幅值键控(ASK)调制方式是指载波信号的幅值随数字基带信号而变化,因此可以实现将基带信号搬移到载波频段。2ASK是利用代表数字信息0或1的基带矩形脉冲去键控一个连续…...
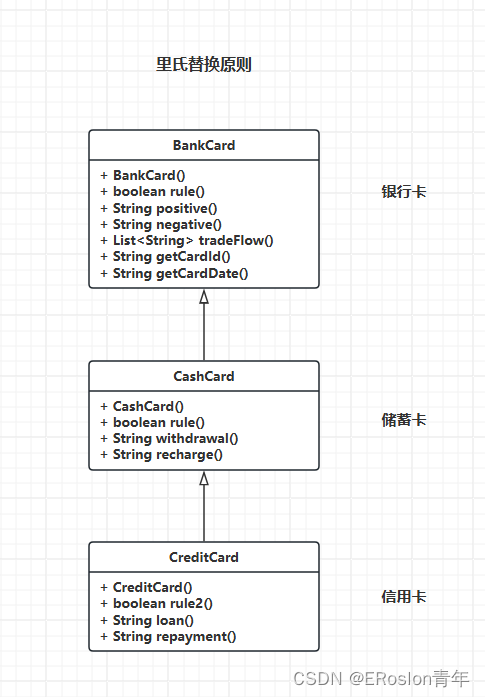
设计模式原则——里氏替换原则
设计模式原则 设计模式示例代码库地址: https://gitee.com/Jasonpupil/designPatterns 里氏替换原则 继承必须确保父类所拥有的性质在子类中依然成立 与开闭原则不同的是开闭原则可以改变父类原有的功能,里氏替换原则不能修改父类的原有的性质&#…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

MyBatis-Plus 常用条件构造方法
1.常用条件方法 方法 说明eq等于 ne不等于 <>gt大于 >ge大于等于 >lt小于 <le小于等于 <betweenBETWEEN 值1 AND 值2notBetweenNOT BETWEEN 值1 AND 值2likeLIKE %值%notLikeNOT LIKE %值%likeLeftLIKE %值likeRightLIKE 值%isNull字段 IS NULLisNotNull字段…...
