常用算法及参考算法 (1)累加 (2)累乘 (3)素数 (4)最大公约数 (5)最值问题 (6)迭代法
常用算法及参考算法
(1)累加
(2)累乘
(3)素数
(4)最大公约数
(5)最值问题
(6)迭代法

1. 累加
#include <stdio.h>int main() {int n, i, sum = 0;printf("Enter a positive integer n: ");scanf("%d", &n);for (i = 1; i <= n; i++) {sum += i;}printf("The sum from 1 to %d is: %d\n", n, sum);return 0;
}
2. 累乘
#include <stdio.h>int main() {int n, i, product = 1;printf("Enter a positive integer n: ");scanf("%d", &n);for (i = 1; i <= n; i++) {product *= i;}printf("The product from 1 to %d is: %d\n", n, product);return 0;
}
3. 素数判断
#include <stdio.h>
#include <stdbool.h>bool isPrime(int num) {if (num <= 1) return false;for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return false;}}return true;
}int main() {int num;printf("Enter a positive integer: ");scanf("%d", &num);if (isPrime(num)) {printf("%d is a prime number.\n", num);} else {printf("%d is not a prime number.\n", num);}return 0;
}
4. 最大公约数(最小公倍数可以通过两数乘积除以最大公约数得到)
#include <stdio.h>int gcd(int a, int b) {if (b == 0) return a;return gcd(b, a % b);
}int main() {int a, b, g;printf("Enter two integers: ");scanf("%d %d", &a, &b);g = gcd(a, b);printf("The GCD of %d and %d is: %d\n", a, b, g);// LCM = (a * b) / GCD(a, b)printf("The LCM of %d and %d is: %d\n", a, b, (a * b) / g);return 0;
}
5. 最值问题(这里以找数组中的最大值为例)
#include <stdio.h>int main() {int arr[] = {5, 2, 9, 1, 5, 6};int size = sizeof(arr) / sizeof(arr[0]);int max = arr[0];for (int i = 1; i < size; i++) {if (arr[i] > max) {max = arr[i];}}printf("The maximum value in the array is: %d\n", max);return 0;
}
6. 迭代法(这里以计算平方根为例,使用牛顿法)
#include <stdio.h>
#include <math.h>double sqrt_iter(double x, double epsilon) {double guess = x / 2.0;while (fabs(guess * guess - x) >= epsilon) {guess = (guess + x / guess) / 2.0;}return guess;
}int main() {double x, epsilon;printf("Enter a number and epsilon: ");scanf("%lf %lf", &x, &epsilon);printf("The square root of %.2lf is approximately %.5lf\n", x, sqrt_iter(x, epsilon));return 0;
}
这些示例代码可能需要根据具体需求进行调整。
相关文章:

常用算法及参考算法 (1)累加 (2)累乘 (3)素数 (4)最大公约数 (5)最值问题 (6)迭代法
常用算法及参考算法 (1)累加 (2)累乘 (3)素数 (4)最大公约数 (5)最值问题 (6)迭代法 1. 累加 #include <stdio.h>int main() {…...
java简易计算器(多种方法)
parseDouble() 方法属于 java.lang.Double 类。它接收一个字符串参数,其中包含要转换的数字表示。如果字符串表示一个有效的 double,它将返回一个 double 值。 应用场景 parseDouble() 方法在以下场景中非常有用: 从用户输入中获取数字&a…...

spring的bean定义和扫描规则
1、bean的基本定义 在Spring框架中,Bean是一个核心概念,它是Spring IoC(Inverse of Control,控制反转)容器管理的一个对象实例。简单来说,Bean就是由Spring容器初始化、配置和管理的对象。这些对象可以是J…...
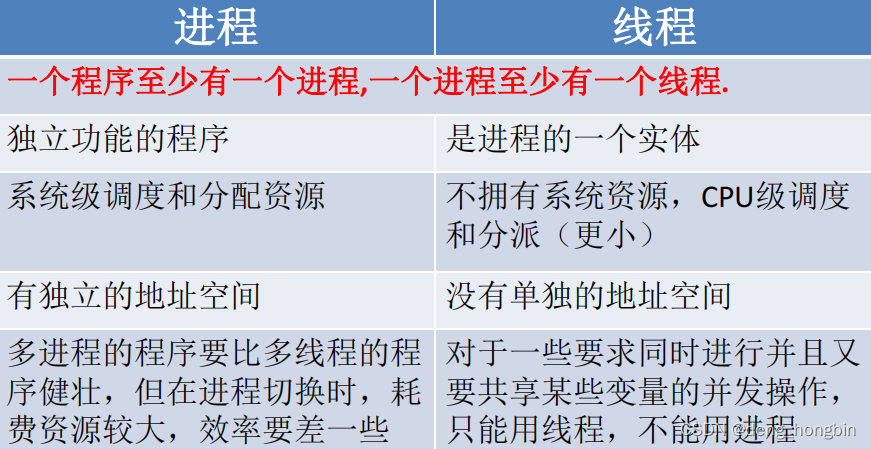
软件工程体系概念
软件工程 软件工程是应用计算机科学、数学及 管理科学等原理开发软件的工程。它借鉴 传统工程的原则、方法,以提高质量,降 低成本为目的。 一、软件生命周期 二、软件开发模型 1.传统模型 瀑布模型、V模型、W模型、X 模型、H 模型 (1)瀑布模型 瀑布…...
史上最全整合nacos单机模式整合哈哈哈哈哈
Nacos 是阿里巴巴推出的一个新开源项目,它主要是一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。 Nacos提供了一组简单易用的特性集,帮助用户快速实现动态服务发现、服务配置、服务元数据及流量管理。 Nacos 的关键特性包括&#x…...

Python xml.dom.minidom 读取XML元素
哈喽,大家好,我是木头左! 什么是 XML? XML(可扩展标记语言)是一种用于描述数据结构和交换数据的标记语言。它被广泛用于 Web 应用程序中,用于存储和传输数据。XML 具有自描述性,因此可以很容易地理解和处理。 Python 中的 xml.dom.minidom Python 提供了一个内置的库…...

【Python/Pytorch 】-- K-means聚类算法
文章目录 文章目录 00 写在前面01 基于Python版本的K-means代码02 X-means方法03 最小二乘法简单理解04 贝叶斯信息准则 00 写在前面 时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数…...

【Eureka】介绍与基本使用
Eureka介绍与基本使用 一个简单的Eureka服务器的设置方法:1 在pom.xml中添加Eureka服务器依赖:2 在application.properties或application.yml中添加Eureka服务器配置:3 创建启动类,使用EnableEurekaServer注解启用Eureka服务器&am…...
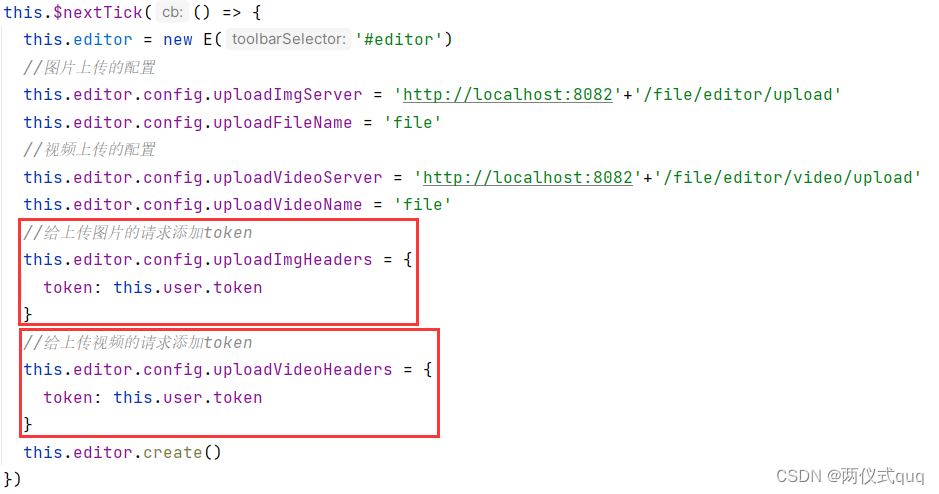
SpringBoot+Vue集成富文本编辑器
1.引入 我们常常在各种网页软件中编写文档的时候,常常会有富文本编辑器,就比如csdn写博客的这个页面,包含了富文本编辑器,那么怎么实现呢?下面来详细的介绍! 2.安装wangeditor插件 在Vue工程中,…...

React@16.x(34)动画(中)
目录 3,SwitchTransition3.1,原理3.1.2,key3.1.2,mode 3.2,举例3.3,结合 animate.css 4,TransitionGroup4.1,其他属性4.1.2,appear4.1.2,component4.1.3&…...

ONLYOFFICE 8.1:全面升级,PDF编辑与本地化加强版
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.1版本新增了那些特别的实用模块? 2.1. 轻松编辑器 PDF 文件 2.2. 用幻灯片版式快速修改幻灯片 2.3. 无缝切换文档编辑、审阅和查…...

C++ 入门
前言 c的发展史: C的起源可以追溯到1979年,当时Bjarne Stroustrup在贝尔实验室开始开发一种名为“C with Classes”的语言。以下是C发展的几个关键阶段: 1979年:Bjarne Stroustrup在贝尔实验室开始开发“C with Classes”。1983…...

GPT-5发布倒计时:AI智能从高中生到博士生的跨越
嘿,小伙伴们!最近有个大新闻,OpenAI的首席技术官米拉穆拉蒂在一次采访中透露,GPT-5将在一年半后发布。她把这个升级比作从聪明的高中生到博学的博士生的飞跃,听起来是不是很酷? 现在GPT-4o还有不少功能没上…...

Docker 拉取镜像失败处理 配置使用代理拉取
解决方案 1、在 /etc/systemd/system/docker.service.d/http-proxy.conf 配置文件中添加代理信息 2、重启docker服务 具体操作如下: 创建 dockerd 相关的 systemd 目录,这个目录下的配置将覆盖 dockerd 的默认配置 代码语言:javascript 复…...

视频汇聚安防综合管理系统EasyCVR平台GB28181设备注册未上线的原因排查与解决
视频汇聚安防综合管理平台EasyCVR视频监控系统基于云边端架构,可支持海量视频汇聚集中管理,能提供视频监控直播、云端录像、云存储、录像检索与回看、告警(协议告警/智能告警/1400视图库告警)、平台级联、AI智能分析接入等视频能力…...
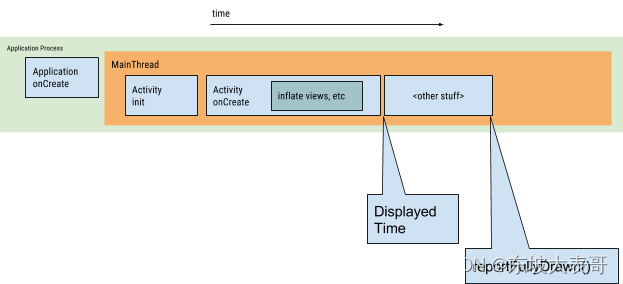
【性能优化】Android冷启动优化
文章目录 常见现象APP的启动流程计算启动时间Displayed Timeadb dump 启动优化具体策略总结参考链接 常见现象 各种第三方工具初始化和大量业务逻辑初始化,影响启动时间,导致应用启动延迟、卡顿等现象 APP的启动流程 加载和启动应用程序; …...

Git拉完整代码缺少某个类
已找到具体问题,对比之后发现应该是拉去的文件名字字符太长导致! 使用 Git LFS Git LFS(Large File Storage)是 Git 的一个扩展,它可以帮助管理大型文件,包括长文件名。如果你的项目包含大量的大型文件或长…...
Windows资源管理器down了,怎么解
ctrlshiftesc 打开任务管理器 文件 运行新任务 输入 Explorer.exe 资源管理器重启 问题解决 桌面也回来了...
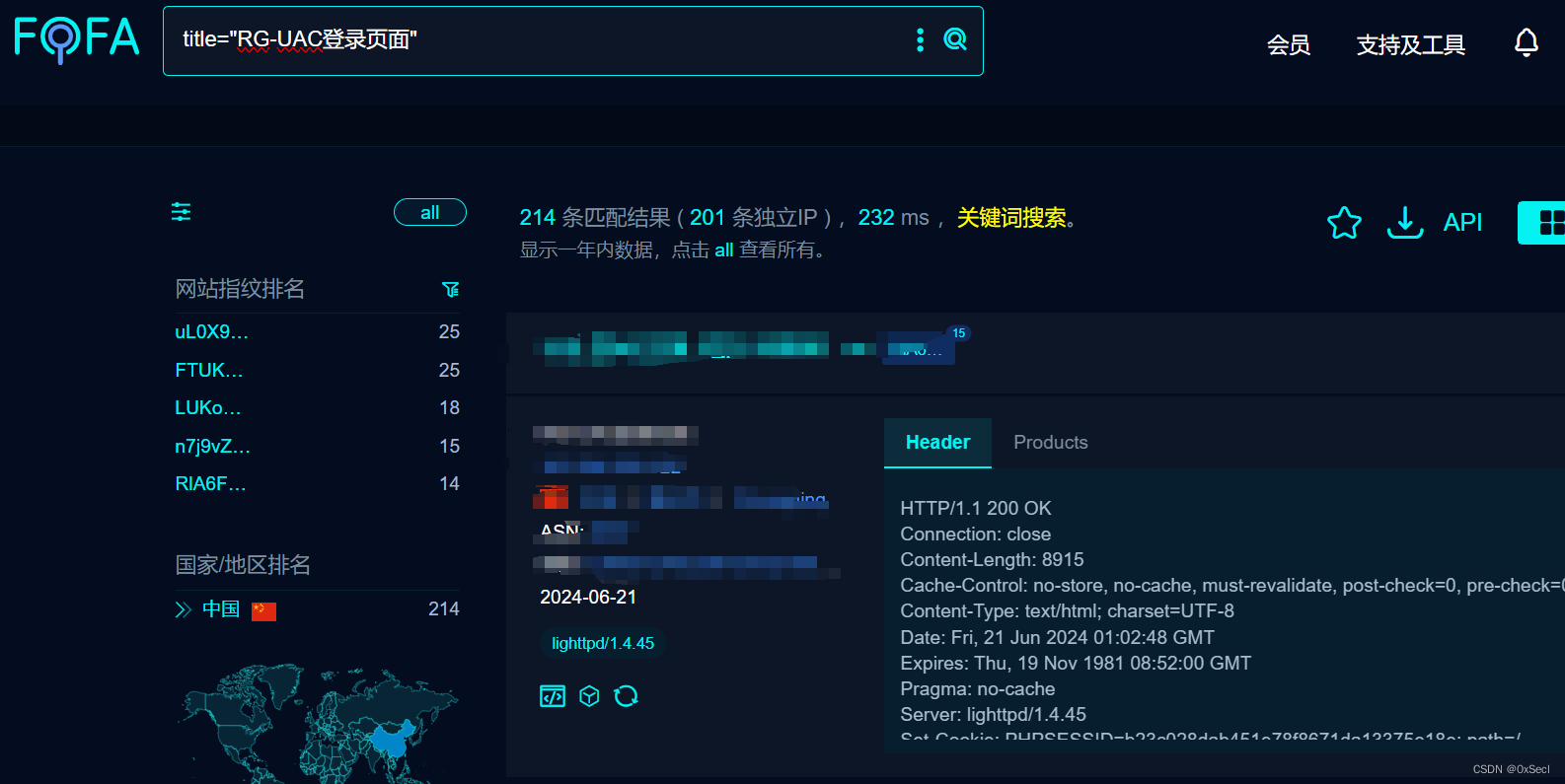
锐捷统一上网行为管理与审计系统 static_convert.php 前台RCE漏洞复现
0x01 产品简介 锐捷统一上网行为管理与审计RG-UAC系列是星网锐捷网络有限公司自主研发的上网行为管理与审计产品,具备的上网行为日志审计功能,能够全面、准确、细致的审计并记录多种上网行为日志,包括网页、搜索、外发文件、邮件、论坛、IM等等,并对日志数据进行统计分析,…...

在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS
在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS 在远程管理服务器时,SSH(Secure Shell)协议是我们常用的工具之一。它提供了一种加密的方式来访问和管理远程主机。默认情况下,SSH使用22端口,但有时我们需要通过指定…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
