【Python/Pytorch 】-- K-means聚类算法

文章目录
文章目录
- 00 写在前面
- 01 基于Python版本的K-means代码
- 02 X-means方法
- 03 最小二乘法简单理解
- 04 贝叶斯信息准则
00 写在前面
时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数值,并且由机器学习决定的集群数量远远小于体素的数量。因此,对一个聚类进行平均可以大大提高聚类级逆解的信噪比,这可以用作体素级优化的鲁棒初始猜测。
在该演变算法的基础上,总结了K-means算法、X-means算法、最小二乘法、贝叶斯信息准则
01 基于Python版本的K-means代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 生成具有三个簇的示例数据
n_samples = 300
n_features = 2
centers = 3
cluster_std = 1.0x, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, cluster_std=cluster_std, random_state=42)# 设置K值(簇的数量)
k = 3# 初始化KMeans算法
kmeans = KMeans(n_clusters=k, random_state=42)# 进行聚类
kmeans.fit(X)# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_# 绘制聚类结果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o', edgecolor='k', s=50)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x', s=200, linewidths=3, zorder=10)
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()
02 X-means方法
传统的K-means聚类算法需要预先确定聚类的数量K。在这里,使用了一种称为X-means的方法,该方法能够自动选择K。X-means方法通过两个步骤反复迭代来选择合适的聚类数量K。
- 步骤1:
- 首先执行传统的K-means聚类,给定一个初始的聚类数量。
- 计算贝叶斯信息准则(BIC),BIC是聚类对数似然和对K的惩罚项的和。
- 随着K的增加,拟合的优度(对数似然)增加,但过拟合的可能性也增加。惩罚项用来减少这种可能性。
- 步骤2:
- 每个聚类的质心(质心)被替换为两个子质心,并在该聚类内使用这些子质心作为初始猜测进行局部K-means(K = 2)。
- 计算该聚类的BIC:如果BIC较大,则进行替换,否则保留“父”质心。
- 重复步骤1和步骤2,直到整体BIC不再增加或 K达到预先设定的最大值为止。
- 在这项研究中,初始聚类数为1,最大聚类数为50。
03 最小二乘法简单理解
最小二乘法(Least Squares Method, LSM)是统计学和数据分析中常用的一种方法,用于拟合数据模型。它的本质是一个优化过程,因为它通过最小化目标函数来找到模型参数的最优解。
(1)最小二乘法的基本思想
假设我们有一组观测数据点(x1, y1),(x2, y2),…,(xn, yn),我们希望找到一个函数 f(x)来拟合这些数据点。最简单的情况是线性拟合,即找到一个直线模型 y=ax+b,使得该直线尽可能靠近所有观测数据点。
最小二乘法的目标是最小化以下目标函数(误差的平方和):
S ( a , b ) = ∑ i = 1 n ( y i − ( a x i + b ) ) 2 S(a,b) = {\textstyle \sum_{i=1}^{n}} (y_{i}-(ax_{i}+b) )^{2} S(a,b)=∑i=1n(yi−(axi+b))2
其中,yi是观测值,axi+b是预测值。
(2)最小二乘法的优化过程
- 步骤1:
定义目标函数:目标函数S(a,b) 表示预测值与观测值之间的误差的平方和。 - 步骤2:
求导数:为了找到使目标函数最小的参数 a 和b,我们对 S(a, b) 分别对a 和 b 求偏导数,并将其设为零,得到一组方程:
∂ S ∂ a = − 2 ∑ i = 1 n x i ( y i − a x i − b ) = 0 \frac{\partial S}{\partial a} = -2 {\textstyle \sum_{i=1}^{n}} x_{i}(y_{i}-ax_{i}-b)=0 ∂a∂S=−2∑i=1nxi(yi−axi−b)=0
∂ S ∂ b = − 2 ∑ i = 1 n ( y i − a x i − b ) = 0 \frac{\partial S}{\partial b} = -2 {\textstyle \sum_{i=1}^{n}} (y_{i}-ax_{i}-b)=0 ∂b∂S=−2∑i=1n(yi−axi−b)=0 - 步骤3:
解方程:通过求解上述方程组,可以得到最优参数 a 和 b 的值。具体求解过程可以得到如下结果:
a = n ∑ i = 1 n x i y i − ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 a = \frac{n {\textstyle \sum_{i=1}^{n}}x_{i}y_{i}-\sum_{i=1}^{n}x_{i}\sum_{i=1}^{n}y_{i} }{n {\textstyle \sum_{i=1}^{n}}x_{i}^{2}-({\textstyle \sum_{i=1}^{n}}x_{i})^{2} } a=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxiyi−∑i=1nxi∑i=1nyi
b = ∑ i = 1 n y i − a ∑ i = 1 n x i n b = \frac{{\textstyle \sum_{i=1}^{n}}y_{i}-a\sum_{i=1}^{n}x_{i}}{n} b=n∑i=1nyi−a∑i=1nxi - 步骤4:
优化的本质:最小二乘法的过程实际上是通过优化方法来最小化目标函数。优化在这里的意思是找到使目标函数达到最小值的参数组合。在最小二乘法中,这个目标函数是误差的平方和,优化过程就是通过求解导数来找到误差平方和的最小值。
04 贝叶斯信息准则
贝叶斯信息准则(Bayesian Information Criterion, BIC)是一种统计量,用于模型选择,特别是在评估模型复杂性和拟合优度之间的平衡时使用。
BIC 的计算公式如下:
B I C = − 2 l n ( L ) + k l n ( n ) BIC=-2ln(L) +kln(n) BIC=−2ln(L)+kln(n)
其中:
- ln(L)是模型的对数似然(log-likelihood)。对数似然度量了模型对数据的拟合优度。对数似然值越大,说明模型越能解释数据。
- k是模型的参数数量。在聚类模型中,参数数量通常包括聚类数K和每个聚类的参数(如均值和方差)。k越大,模型越复杂。
- n是样本数量。样本数量是指数据中的观测值个数。
- BIC 的公式中,-2ln(L)代表了模型的拟合优度,值越小,拟合越好。kln(n)是对模型复杂性的惩罚项,随着参数数量 k 和样本数量n的增加,惩罚项也增加。这个项用来防止过拟合。BIC 的值越小,模型越好。因此,在选择模型时,希望找到使 BIC 最小的模型。
相关文章:

【Python/Pytorch 】-- K-means聚类算法
文章目录 文章目录 00 写在前面01 基于Python版本的K-means代码02 X-means方法03 最小二乘法简单理解04 贝叶斯信息准则 00 写在前面 时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数…...

【Eureka】介绍与基本使用
Eureka介绍与基本使用 一个简单的Eureka服务器的设置方法:1 在pom.xml中添加Eureka服务器依赖:2 在application.properties或application.yml中添加Eureka服务器配置:3 创建启动类,使用EnableEurekaServer注解启用Eureka服务器&am…...
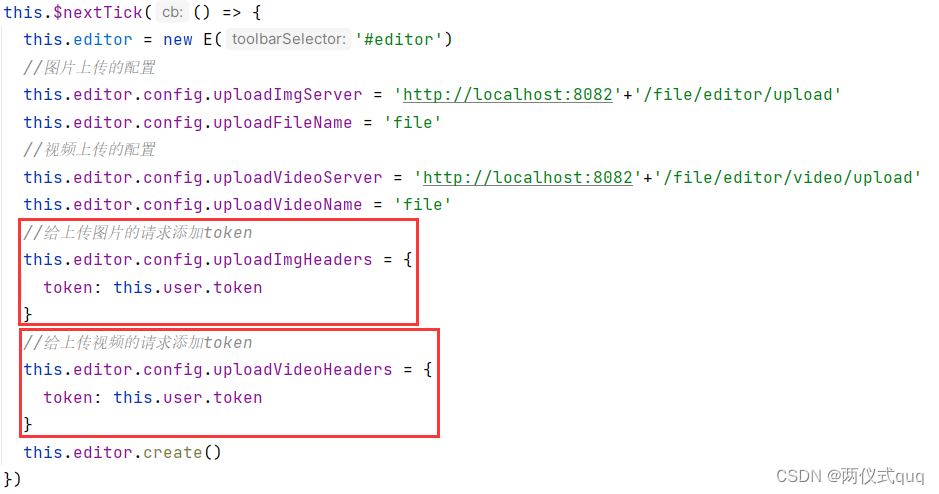
SpringBoot+Vue集成富文本编辑器
1.引入 我们常常在各种网页软件中编写文档的时候,常常会有富文本编辑器,就比如csdn写博客的这个页面,包含了富文本编辑器,那么怎么实现呢?下面来详细的介绍! 2.安装wangeditor插件 在Vue工程中,…...

React@16.x(34)动画(中)
目录 3,SwitchTransition3.1,原理3.1.2,key3.1.2,mode 3.2,举例3.3,结合 animate.css 4,TransitionGroup4.1,其他属性4.1.2,appear4.1.2,component4.1.3&…...

ONLYOFFICE 8.1:全面升级,PDF编辑与本地化加强版
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.1版本新增了那些特别的实用模块? 2.1. 轻松编辑器 PDF 文件 2.2. 用幻灯片版式快速修改幻灯片 2.3. 无缝切换文档编辑、审阅和查…...

C++ 入门
前言 c的发展史: C的起源可以追溯到1979年,当时Bjarne Stroustrup在贝尔实验室开始开发一种名为“C with Classes”的语言。以下是C发展的几个关键阶段: 1979年:Bjarne Stroustrup在贝尔实验室开始开发“C with Classes”。1983…...

GPT-5发布倒计时:AI智能从高中生到博士生的跨越
嘿,小伙伴们!最近有个大新闻,OpenAI的首席技术官米拉穆拉蒂在一次采访中透露,GPT-5将在一年半后发布。她把这个升级比作从聪明的高中生到博学的博士生的飞跃,听起来是不是很酷? 现在GPT-4o还有不少功能没上…...

Docker 拉取镜像失败处理 配置使用代理拉取
解决方案 1、在 /etc/systemd/system/docker.service.d/http-proxy.conf 配置文件中添加代理信息 2、重启docker服务 具体操作如下: 创建 dockerd 相关的 systemd 目录,这个目录下的配置将覆盖 dockerd 的默认配置 代码语言:javascript 复…...

视频汇聚安防综合管理系统EasyCVR平台GB28181设备注册未上线的原因排查与解决
视频汇聚安防综合管理平台EasyCVR视频监控系统基于云边端架构,可支持海量视频汇聚集中管理,能提供视频监控直播、云端录像、云存储、录像检索与回看、告警(协议告警/智能告警/1400视图库告警)、平台级联、AI智能分析接入等视频能力…...
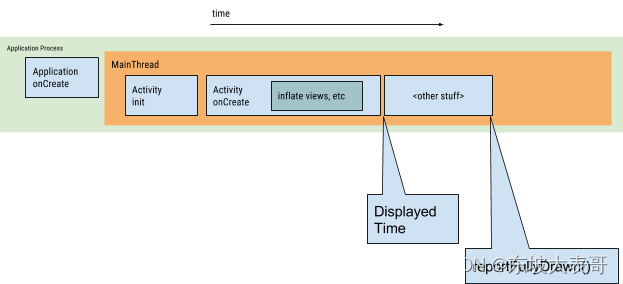
【性能优化】Android冷启动优化
文章目录 常见现象APP的启动流程计算启动时间Displayed Timeadb dump 启动优化具体策略总结参考链接 常见现象 各种第三方工具初始化和大量业务逻辑初始化,影响启动时间,导致应用启动延迟、卡顿等现象 APP的启动流程 加载和启动应用程序; …...

Git拉完整代码缺少某个类
已找到具体问题,对比之后发现应该是拉去的文件名字字符太长导致! 使用 Git LFS Git LFS(Large File Storage)是 Git 的一个扩展,它可以帮助管理大型文件,包括长文件名。如果你的项目包含大量的大型文件或长…...
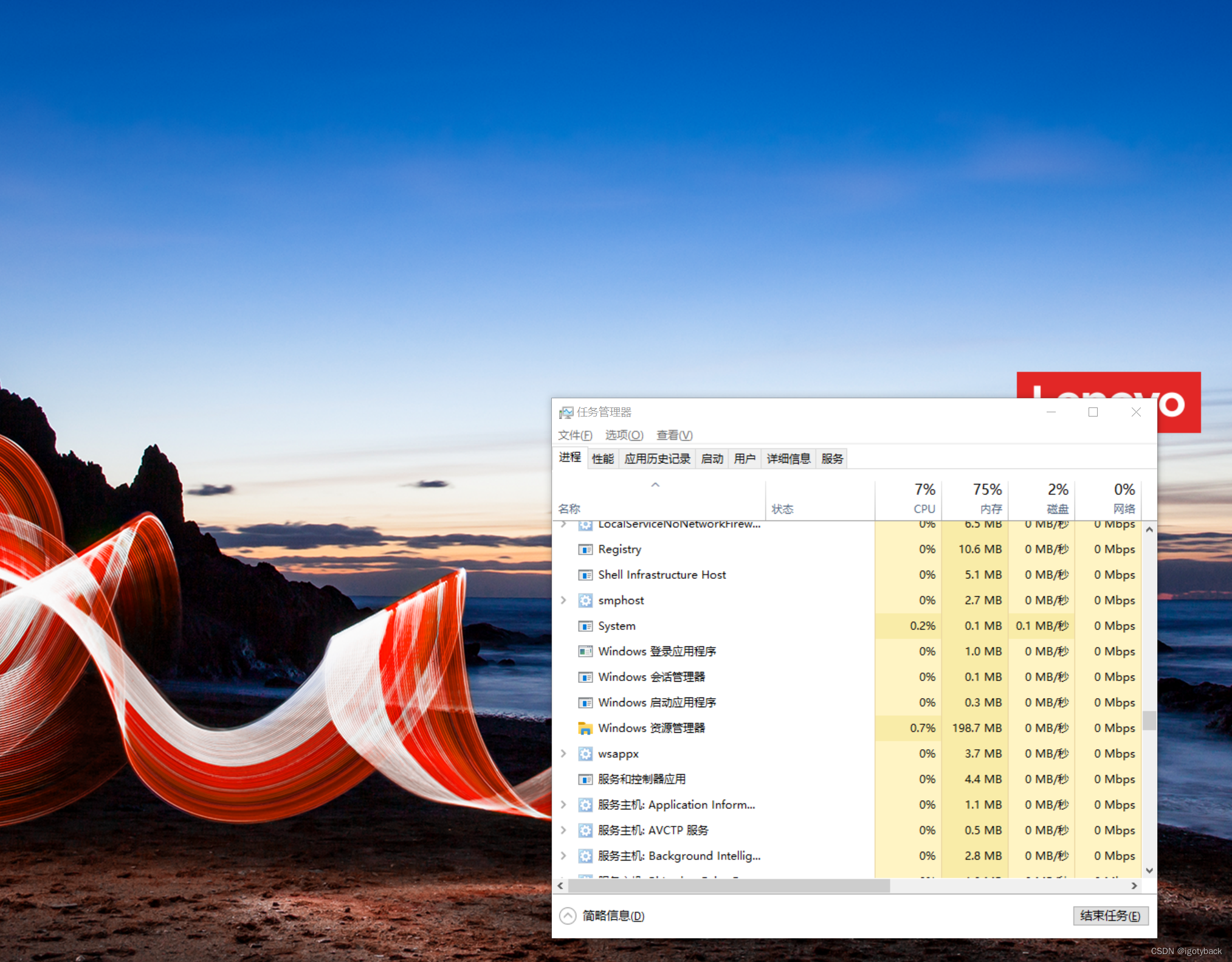
Windows资源管理器down了,怎么解
ctrlshiftesc 打开任务管理器 文件 运行新任务 输入 Explorer.exe 资源管理器重启 问题解决 桌面也回来了...
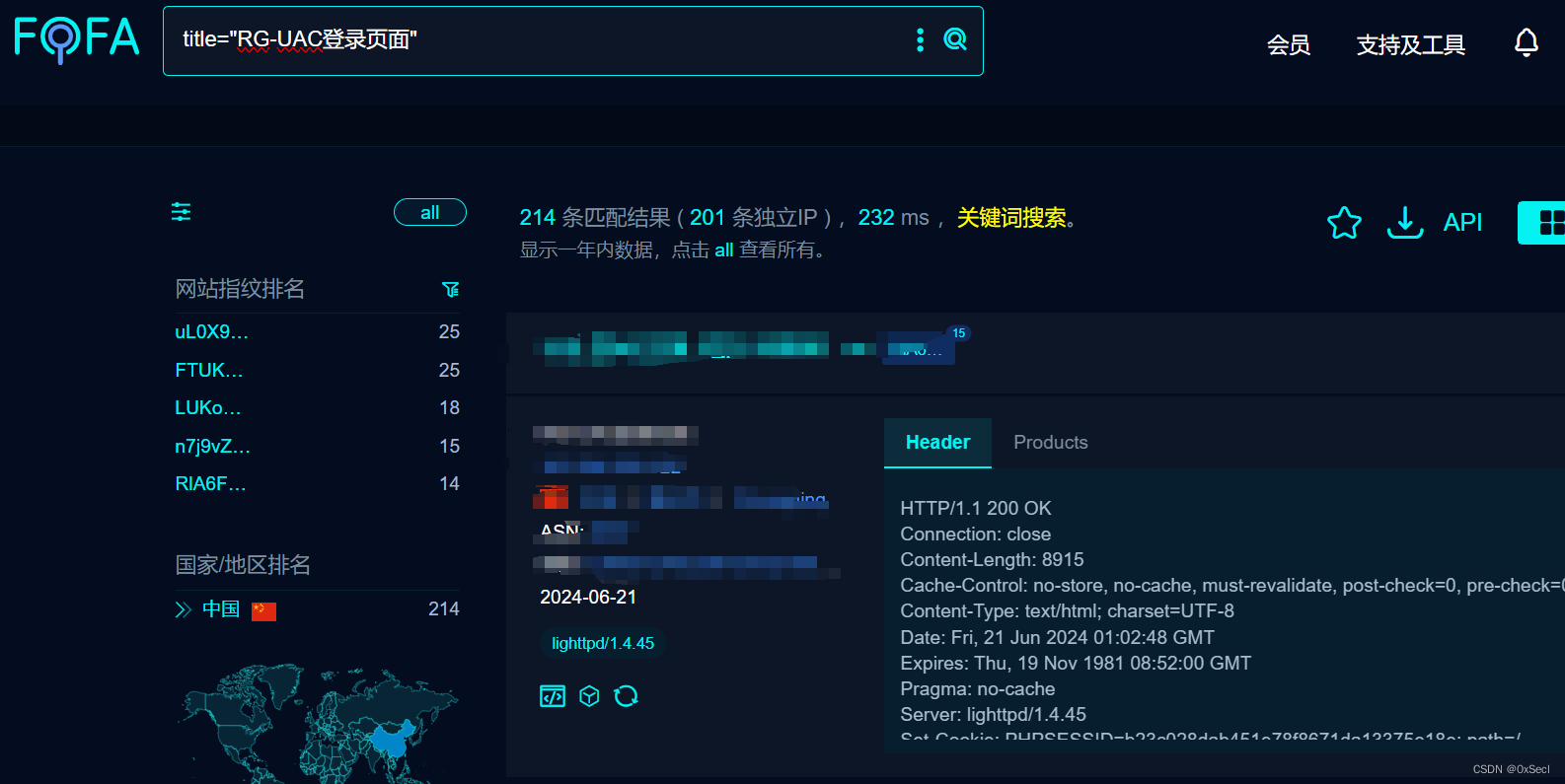
锐捷统一上网行为管理与审计系统 static_convert.php 前台RCE漏洞复现
0x01 产品简介 锐捷统一上网行为管理与审计RG-UAC系列是星网锐捷网络有限公司自主研发的上网行为管理与审计产品,具备的上网行为日志审计功能,能够全面、准确、细致的审计并记录多种上网行为日志,包括网页、搜索、外发文件、邮件、论坛、IM等等,并对日志数据进行统计分析,…...

在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS
在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS 在远程管理服务器时,SSH(Secure Shell)协议是我们常用的工具之一。它提供了一种加密的方式来访问和管理远程主机。默认情况下,SSH使用22端口,但有时我们需要通过指定…...

如何安全进行亚马逊、沃尔玛测评?
在亚马逊、沃尔玛、速卖通、阿里国际站等电商平台上,测评已成为一种高效的推广手段,但伴随的风险也不容忽视。这些风险主要源于平台严格的大数据风控机制,它涵盖了多个方面,以确保评价的真实性和合规性。 首先,硬件参数…...

自动化喷涂生产线控制方法概述
喷涂生产线涉及控制机械臂及传送带等,以及触摸屏人机界面,以及各种电机,电磁阀等,本文针对具体控制方法进行讨论。 一套自动化喷涂生产线装配完成后,进入到控制调试阶段,首先要进行工艺参数的设置ÿ…...
【Linux】Centos升级到国产操作系统Openeuler
一、前言 迁移工具采用Openeuler官网提供的x2openEuler工具,是一款将源操作系统迁移到目标操作系统的迁移工具套件,具有批量化原地升级能力,当前支持将源 OS 升级至 openEuler 20.03。 官网链接:openEuler迁移专区 | 迁移专区首页…...

【扫雷游戏】C语言详解
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...

自定义平台后台登录地址前缀的教程
修改平台后台地址默认的 admin 前缀 修改后端 config/admin.php 配置文件,为自定义的后缀修改 平台后台前端源码中 src/settings.js 文件,修改为和上面一样的配置修改后重新打包前端代码,并且覆盖到后端的 public 目录下重启 swoole 服务即可...

kylin v10 离线安装chrome centos离线安装chrome linux离线安装谷歌浏览器
1. 先用自己联网的计算机,下载离线安装包,浏览器输入链接下载安装包: https://dl.google.com/linux/direct/google-chrome-stable_current_x86_64.rpm 1.2. 信创环境不用执行下面,因为没网 1.3. 若为阿里云服务器,或服…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
