【C++进阶】四、红黑树(三)
目录
一、红黑树的概念
二、红黑树的性质
三、红黑树节点的定义
四、红黑树的插入
五、红黑树的验证
六、红黑树与AVL树的比较
七、完整代码
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的
如下图就是一棵红黑树:
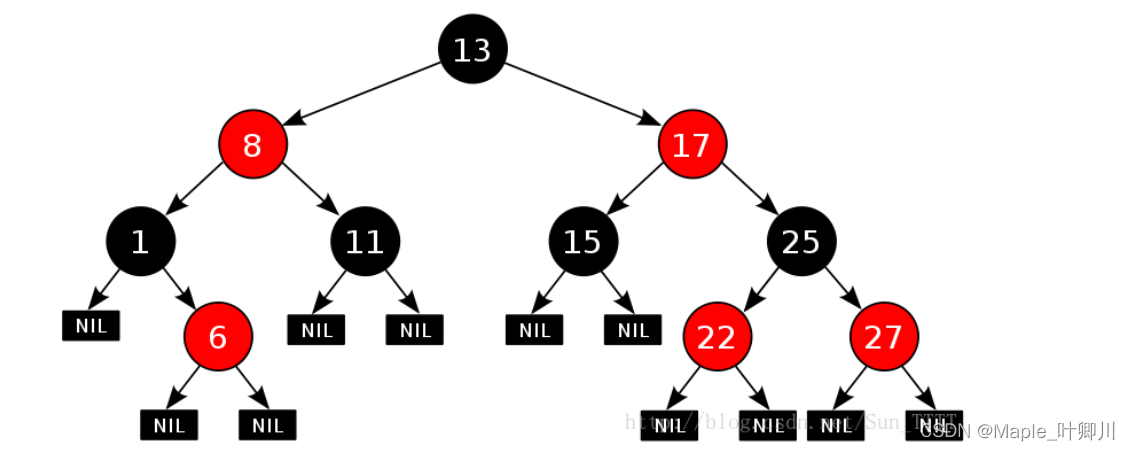
二、红黑树的性质
红黑树有以下性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的,即没有连续红色节点
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,如上图的NIL节点)
- 红黑树最优情况(左右平衡):全黑或每条路径都是一黑一红相间的满二叉树,搜索高度 logN
- 红黑树最差情况(左右极不平衡):每颗子树左子树全黑,右子树一黑一红,搜索高度 2*logN
红黑树不追求极致的平衡,AVL树则是追求极致的平衡,红黑树是近似平衡;红黑树这种近似平衡的结构大大减少了大量的旋转,红黑树的综合性能优于 AVL树
为什么红黑树满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
- 红黑树的最短路径:全黑,一条路径上的全是黑色节点
- 红黑树的最长路径:一黑一红相间的路径
比如:
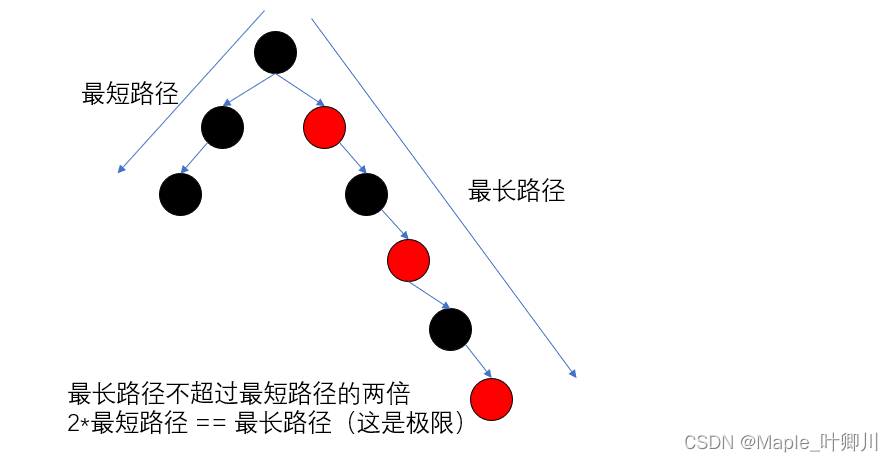
三、红黑树节点的定义
红黑树也是使用键值对,即KV模型,也是为了方便后序操作,红黑树的结构也是三叉链,即增加了指向父节点的 parent指针,还增加了一个成员变量,用于标识节点的颜色(red or black)
enum Colour
{RED,BLACK,
};//K:key, V:value
template<class K, class V>
struct RBTreeNode
{//构造函数RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}//成员变量pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:private:Node* _root = nullptr;//缺省值
};
注:这里使用了枚举来列举颜色
为什么构造红黑树结点时,默认将结点的颜色设置为红色?
- 插入结点如果是黑色的,一定破坏红黑树的性质4,无论如何都必须对红黑树进行调整。
- 插入结点如果是红色的,可能破坏红黑树的性质3,可能需要对红黑树进行调整 或者不需要调整
所以将节点颜色默认设置为红色
四、红黑树的插入
红黑树的插入分两步:
- 按照二叉搜索树的方式插入新节点
- 判断是否需要对红黑树进行调整
(1)插入节点
因为红黑树本身就是一棵二叉搜索树,因此寻找结点的插入位置是非常简单的,按照二叉搜索树的插入规则:
- 待插入结点的key值比当前结点小就插入到该结点的左子树
- 待插入结点的key值比当前结点大就插入到该结点的右子树
- 待插入结点的key值与当前结点的 key 值相等就插入失败
(2)判断是否需要对红黑树进行调整
判断:插入节点的父亲 parent 存在且为红色,则需要进行调整,否则不需要
然后分两种情况:
- (A)parent在 grandfather 的左边
- (B)parent在 grandfather 的右边
注:进行调整的关键是 uncle
(A)parent在 grandfather 的左边有三种情况:
- 情况1:uncle存在且为红,uncle和parent的颜色需要修改为黑,granfather 修改为红,如果满足循环条件继续往上更新
- 情况2:uncle存在且为黑,需要对红黑树进行旋转
- 情况3:uncle不存在,需要对红黑树进行旋转
情况1,图如下:
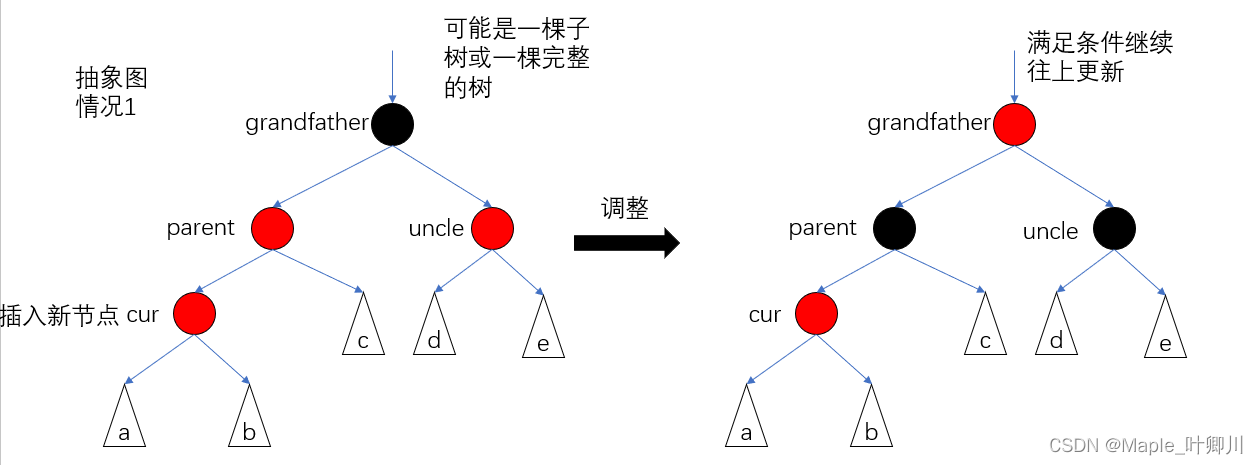
注:情况2和情况3是一起处理的
情况2 + 情况3:
- cur,parent,grandfather 三个节点在一条直线上,单旋处理即可,对 grandfater 进行右单旋,然后 parent 的颜色改为黑,grandfater 的颜色改为红
- cur,parent,grandfather 三个节点是折线,需要双旋处理,对 parent 进行左单旋,然后对 grandfater 进行右单旋,然后 cur 的颜色改为黑,grandfater 的颜色改为红
情况2,图如下:
cur,parent,grandfather 三个节点在一条直线上
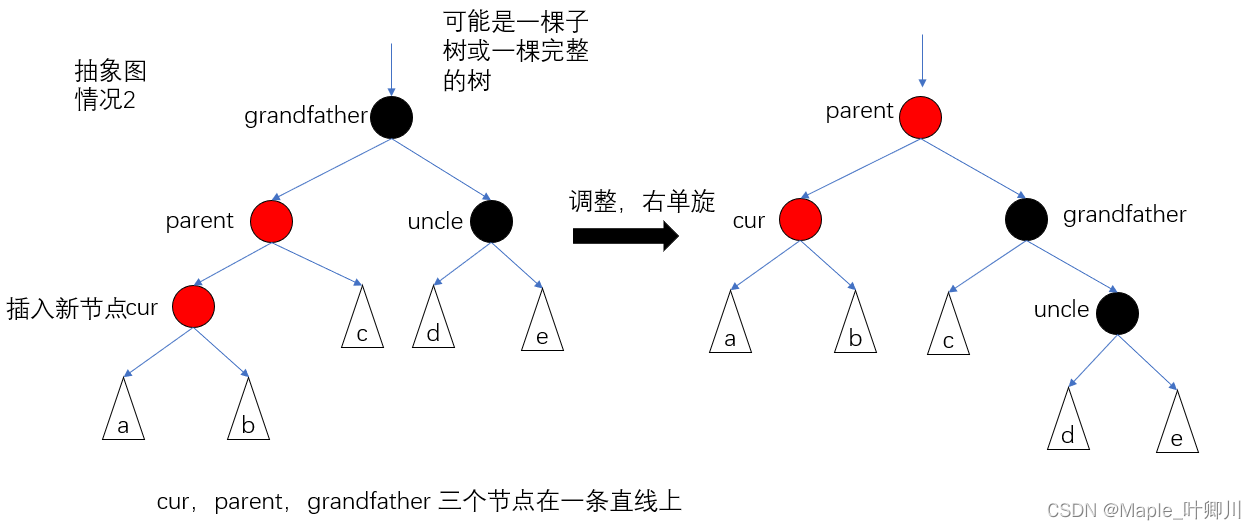
调颜色
 cur,parent,grandfather 三个节点是折线
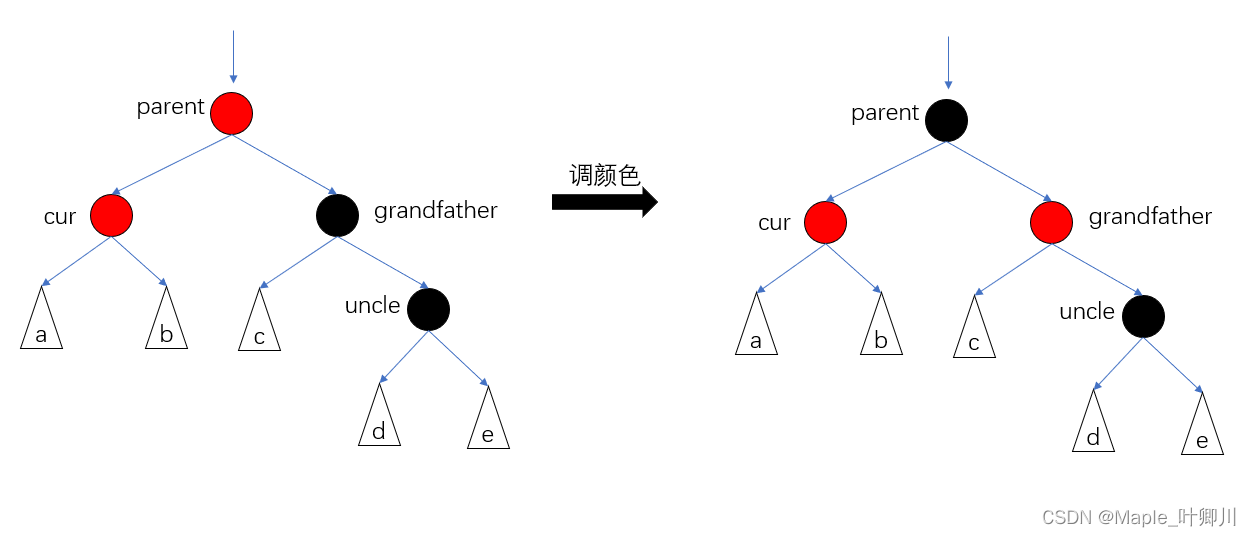
cur,parent,grandfather 三个节点是折线
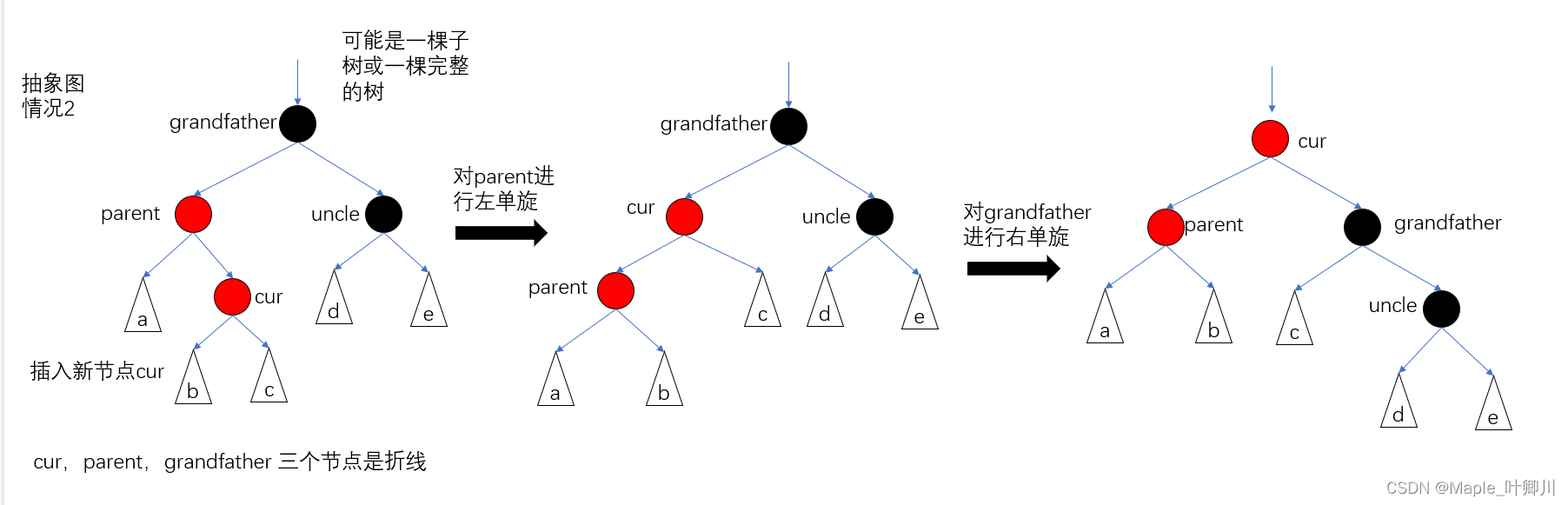
调颜色
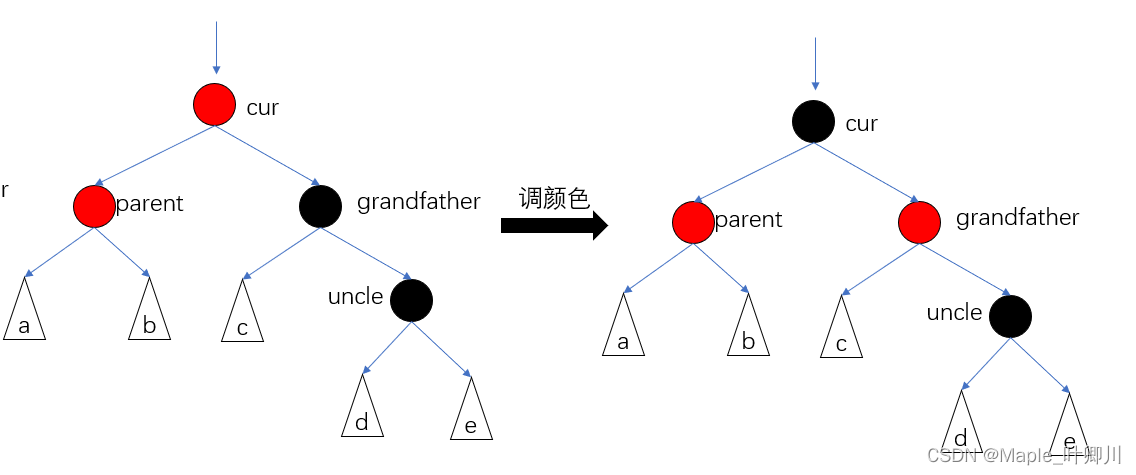
情况3,图如下:
cur,parent,grandfather 三个节点在一条直线上
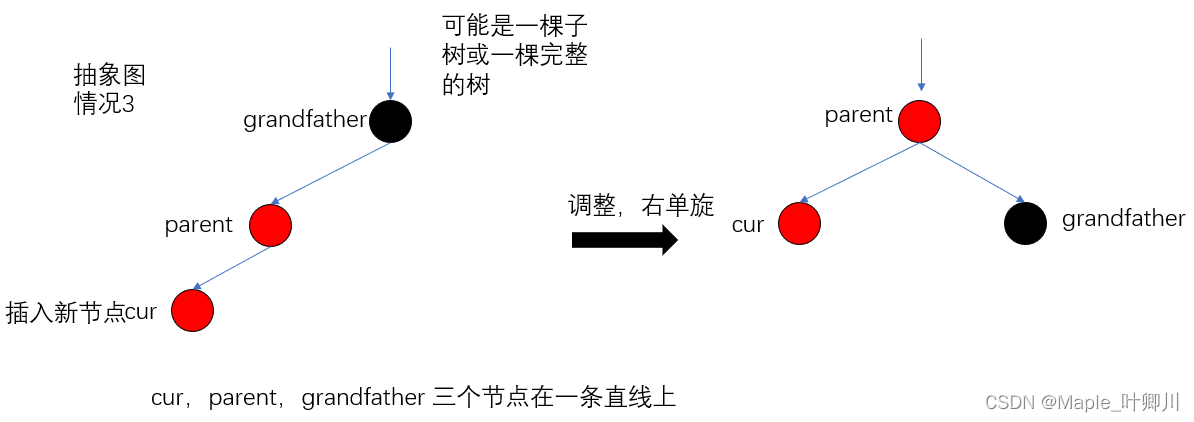
调颜色
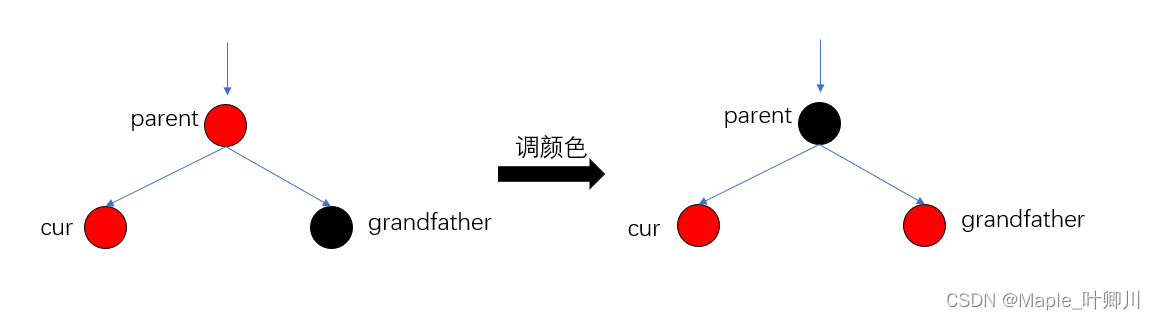
cur,parent,grandfather 三个节点是折线
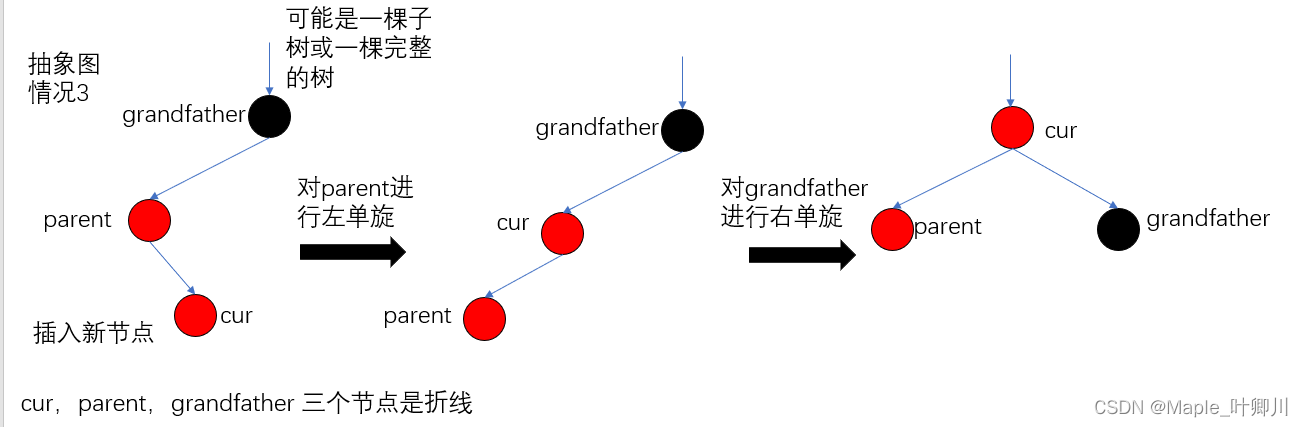
调颜色
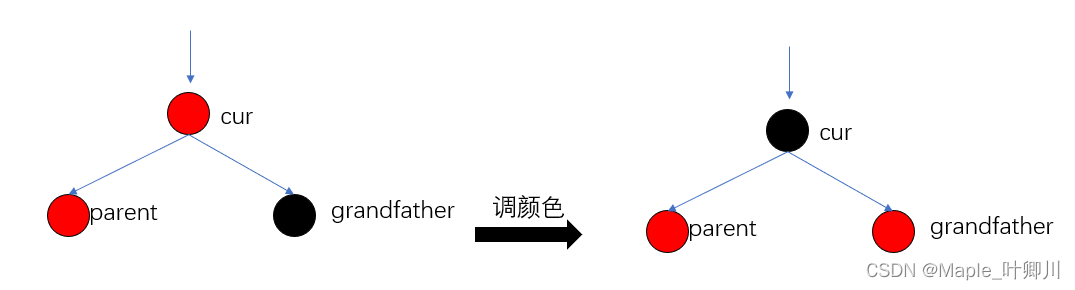
(B)parent在 grandfater 的右边也有三种情况:(与左边情况完全一致,只是旋转不同)
- 情况1:uncle存在且为红,uncle和parent的颜色需要修改为黑,grandfater修改为红,如果满足循环条件继续往上更新
- 情况2:uncle存在且为黑,需要对红黑树进行旋转,对 grandfather 进行右单旋
- 情况3:uncle不存在,需要对红黑树进行双旋转,对 parent 进行左单旋,然后对 grandfather 进行右单旋
注:情况2和情况3是一起处理的
情况2 + 情况3:
- cur,parent,grandfather 三个节点在一条直线上,单旋处理即可,对 grandfather 进行左单旋,然后 parent 的颜色改为黑,grandfater 的颜色改为红
- cur,parent,grandfather 三个节点是折线,需要双旋处理,对 parent 进行右单旋,然后对 grandfather 进行左单旋,然后 cur 的颜色改为黑,grandfather 的颜色改为红
图就不画了,左边的图反过来就是右边的图,旋转在 AVL树有解释,这里就不再解释
经调整后,保持了红黑树的特性
插入代码如下:
//插入
bool Insert(const pair<K, V>& kv)
{//节点为空,新建根节点if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点默认为黑色return true;}//节点为不空Node* parent = nullptr;//用于记录上一个节点Node* cur = _root;//寻找合适的位置进行插入while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else//cur->kv.first == kv.first要插入值已经存在,插入失败{return false;}}cur = new Node(kv);cur->_col = RED;//新节点默认为红//插入if (parent->_kv.first < kv.first)//插入到parent左边{parent->_right = cur;cur->_parent = parent;}else//插入到parent右边{parent->_left = cur;cur->_parent = parent;}//进行调平衡 && 保持红黑树的特性,即插入节点的父亲是红色,需要对红黑树进行调整while (parent && parent->_col == RED)//parent存在且为红 进行调整{Node* grandfather = parent->_parent;//(1)parent在grandfater的左边//(2)parent在grandfater的右边if (parent == grandfather->_left)//parent在grandfater的左边{//情况1:uncle存在且为红,uncle和parent的颜色需要修改为黑,grandfater修改为红,如果满足循环条件继续往上更新//情况2:uncle存在且为黑,需要对红黑树进行旋转//情况3:uncle不存在,需要对红黑树进行旋转//注:情况2和情况3是一起处理的Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//情况1{//修改颜色uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//迭代往上更新cur = grandfather;parent = cur->_parent;}else//情况2 + 情况3{if (cur == parent->_left)//cur,parent,grandfater三个节点在一条直线上,单旋处理即可{RotateR(grandfather);//右单旋parent->_col = BLACK;grandfather->_col = RED;}else//cur,parent,grandfater三个节点是折线,需要双旋处理{RotateL(parent);//左单旋RotateR(grandfather);//右单旋cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后,该子树的根变成了黑色,符合红黑树的特性,无需继续往上处理}}else//parent在grandfater的右边{//在右边 也是上面左边的三种情况Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//情况1{//修改颜色uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//迭代往上更新cur = grandfather;parent = cur->_parent;}else//情况2 + 情况3{if (cur == parent->_right)//cur,parent,grandfater三个节点在一条直线上,单旋处理即可{RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur,parent,grandfater三个节点是折线,需要双旋处理{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后,该子树的根变成了黑色,符合红黑树的特性,无需继续往上处理}}}_root->_col = BLACK;//根的颜色需要变为黑(原因是可能情况1会把根节点变红)return true;
}注:红黑树其他接口就不实现了,在面试考的花也是考查红黑树的插入,即红黑树如何调平衡
五、红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
(1)中序检查
//中序遍历
void InOrder()
{_InOrder(_root);
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}(2)检查红黑树特性
//检查红黑树特性
bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col != BLACK){cout << "违反规则:根节点不为黑色" << endl;return false;}Node* left = _root;int ref = 0;//用于一条路径上记录黑色节点的数量while (left)//求一条路径的黑色节点{if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);
}//检查每条路径的黑色节点是否相等 && 是否出现连续红色节点
bool Check(Node* root, int blackNum, int ref)
{if (root == nullptr){if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);
}六、红黑树与AVL树的比较
红黑树和 AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(logN),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比 AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多
红黑树的应用:
- C++ STL库 -- map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
七、完整代码
RBTree.h
#pragma onceenum Colour
{RED,BLACK,
};//K:key, V:value
template<class K, class V>
struct RBTreeNode
{//构造函数RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}//成员变量pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://插入bool Insert(const pair<K, V>& kv){//节点为空,新建根节点if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点默认为黑色return true;}//节点为不空Node* parent = nullptr;//用于记录上一个节点Node* cur = _root;//寻找合适的位置进行插入while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else//cur->kv.first == kv.first要插入值已经存在,插入失败{return false;}}cur = new Node(kv);cur->_col = RED;//新节点默认为红//插入if (parent->_kv.first < kv.first)//插入到parent左边{parent->_right = cur;cur->_parent = parent;}else//插入到parent右边{parent->_left = cur;cur->_parent = parent;}//进行调平衡 && 保持红黑树的特性,即插入节点的父亲是红色,需要对红黑树进行调整while (parent && parent->_col == RED)//parent存在且为红 进行调整{Node* grandfather = parent->_parent;//(1)parent在grandfater的左边//(2)parent在grandfater的右边if (parent == grandfather->_left)//parent在grandfater的左边{//情况1:uncle存在且为红,uncle和parent的颜色需要修改为黑,grandfater修改为红,如果满足循环条件继续往上更新//情况2:uncle存在且为黑,需要对红黑树进行旋转//情况3:uncle不存在,需要对红黑树进行旋转//注:情况2和情况3是一起处理的Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//情况1{//修改颜色uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//迭代往上更新cur = grandfather;parent = cur->_parent;}else//情况2 + 情况3{if (cur == parent->_left)//cur,parent,grandfater三个节点在一条直线上,单旋处理即可{RotateR(grandfather);//右单旋parent->_col = BLACK;grandfather->_col = RED;}else//cur,parent,grandfater三个节点是折线,需要双旋处理{RotateL(parent);//左单旋RotateR(grandfather);//右单旋cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后,该子树的根变成了黑色,符合红黑树的特性,无需继续往上处理}}else//parent在grandfater的右边{//在右边 也是上面左边的三种情况Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//情况1{//修改颜色uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//迭代往上更新cur = grandfather;parent = cur->_parent;}else//情况2 + 情况3{if (cur == parent->_right)//cur,parent,grandfater三个节点在一条直线上,单旋处理即可{RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur,parent,grandfater三个节点是折线,需要双旋处理{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后,该子树的根变成了黑色,符合红黑树的特性,无需继续往上处理}}}_root->_col = BLACK;//根的颜色需要变为黑(原因是可能情况1会把根节点变红)return true;}//中序遍历void InOrder(){_InOrder(_root);}//检查红黑树特性bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){cout << "违反规则:根节点不为黑色" << endl;return false;}Node* left = _root;int ref = 0;//用于一条路径上记录黑色节点的数量while (left)//求一条路径的黑色节点{if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);}
private://检查每条路径的黑色节点是否相等 && 是否出现连续红色节点bool Check(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//进行链接parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;//记录parent节点的前一个节点subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr)//即subR已经是根节点{_root = subR;_root->_parent = nullptr;}else//subR不是根节点{//与上一个节点进行链接if (ppNode->_left == parent)//parent原本在 ppNode 的左边{ppNode->_left = subR;}else//parent原本在 ppNode 的右边{ppNode->_right = subR;}subR->_parent = ppNode;}}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//进行链接parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;//记录parent节点的前一个节点subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr)//即subL已经是根节点{_root = subL;subL->_parent = nullptr;}else//subR不是根节点{//与上一个节点进行链接if (ppNode->_left == parent)//parent原本在 ppNode 的左边{ppNode->_left = subL;}else//parent原本在 ppNode 的右边{ppNode->_right = subL;}subL->_parent = ppNode;}}
private:Node* _root = nullptr;//缺省值
};
Test.cpp
#include <iostream>
using namespace std;
#include "RBTree.h"void TestRBTree1()
{//int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : arr){t.Insert(make_pair(e, e));}t.InOrder();
}void TestRBTree2()
{srand(time(0));//随机数种子const size_t N = 100000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}cout << t.IsBalance() << endl;
}int main()
{TestRBTree2();return 0;
}----------------我是分割线---------------
文章到这里就结束了,下一篇即将更新
相关文章:

【C++进阶】四、红黑树(三)
目录 一、红黑树的概念 二、红黑树的性质 三、红黑树节点的定义 四、红黑树的插入 五、红黑树的验证 六、红黑树与AVL树的比较 七、完整代码 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可…...
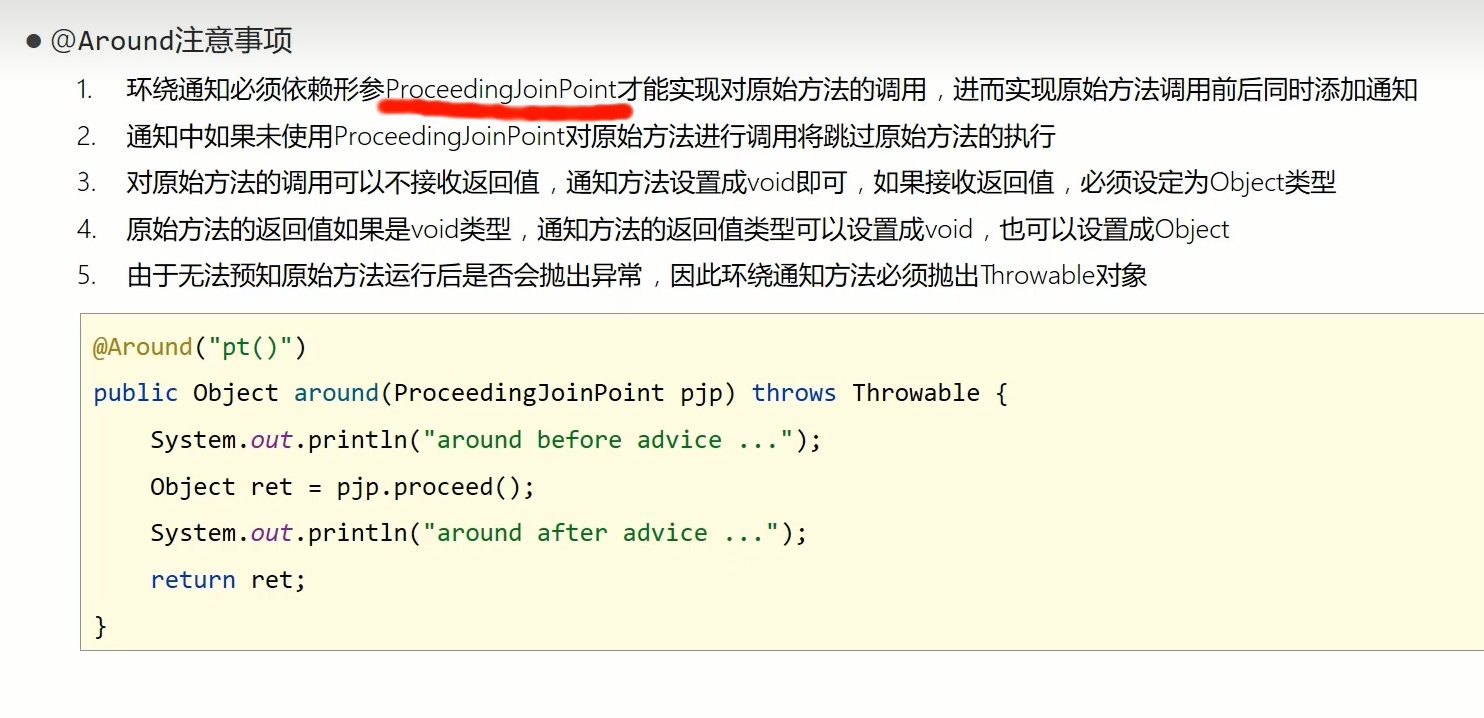
Spring——AOP切入点表达式和AOP通知类型
切入点:要进行增强的方法 切入点表达式:要进行增强的方法的描述式 第一种方法的本质是基于接口实现的动态代理(jdk) 第二种是基于cglib实现的动态代理 AOP切入点表达式 而需要加载多个切入点时,不可能每个切入点都写一个切入点表达式 例子 下面的代理描述的是匹配…...

Hadoop学习:Yarn
1.YARN介绍 一个通用的资源管理系统和调度平台 YARN不分配磁盘,由HDFS分配 相当于一个分布式的操作系统平台,为上层MR等计算程序提供运算所需要的资源(内存、CPU等) 2.YARN三大组件 不要忘记AppMaster,他是程序内部…...

Spring Data JPA
文章目录一、Spring Data基础概念二、JPA与JDBC的相同与不同之处三、Hibernate & JPA快速搭建1.添加依赖2.实体类3.hibernate的配置文件 ——hibernate.cfg.xml四、测试——基于hibernate的持久化(单独使用)五、测试——基于JPA的持久化(…...

java List报错Method threw ‘java.lang.UnsupportedOperationException‘ exception. 解决
问题描述:List使用Arrays.asList()初始化后,再add对象时报错:Method threw java.lang.UnsupportedOperationException exception.错误示例如下: List<ExportListVO.ExportSheet> sheetVOList Arrays.asList(new ExportList…...
数据结构-用栈实现队列
前言: 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾 int pop() 从队列的开头移除并返回元素 int…...

第十四章 从 Windows 客户端控制 IRIS
文章目录第十四章 从 Windows 客户端控制 IRISIRISctlGetDirsSyntaxReturn ValuesIRISctlConfigStatusSyntaxReturn ValuesIRISctlControlSyntaxReturn Values第十四章 从 Windows 客户端控制 IRIS IRIS 为 Windows 客户端程序提供了一种机制来控制 IRIS 配置并启动 IRIS 进程…...
数据结构---双链表
专栏:数据结构 个人主页:HaiFan. 专栏简介:从零开始,数据结构!! 双链表前言双链表各接口的实现为要插入的值开辟一块空间BuyLN初始化LNInit和销毁LNDestory打印链表中的值LNPrint尾插LNPushBack和尾删LNPop…...

Windows 环境安装Scala详情
为了进一步学习Spark,必须先学习Scala 编程语言。首先开始Scala 环境搭建。温馨提示:本文是基于Windows 11 安装Scala 2.13.1 版本第一步:确保本机已经正确安装JDK1.8 环境第二步:Scala 官网下载我们所属scala版本文件。Scala 官网…...
C++ Qt自建网页浏览器
C Qt自建网页浏览器如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助!前言这篇博客针对<<C Qt自建网页浏览器>>编写代码,代码整洁,规则,易读。 学习与应用推荐首选。文…...
Flink从入门到精通系列(四)
5、DataStream API(基础篇) Flink 有非常灵活的分层 API 设计,其中的核心层就是 DataStream/DataSet API。由于新版本已经实现了流批一体,DataSet API 将被弃用,官方推荐统一使用 DataStream API 处理流数据和批数据。…...
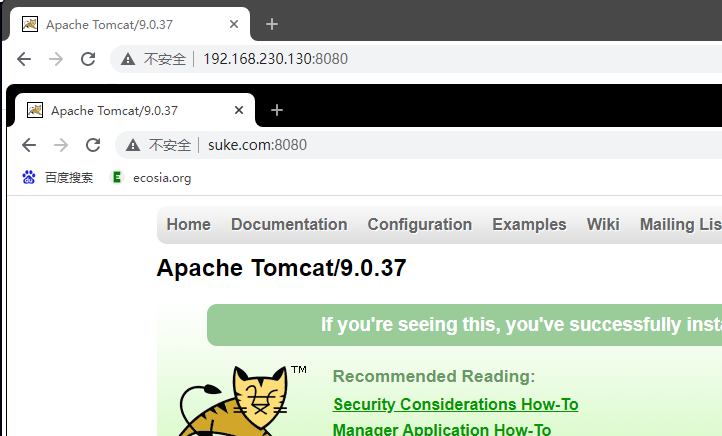
Nginx 配置实例-反向代理案例一
实现效果:使用nginx反向代理,访问 www.suke.com 直接跳转到本机地址127.0.0.1:8080 一、准备工作 Centos7 安装 Nginxhttps://liush.blog.csdn.net/article/details/125027693 1. 启动一个 tomcat Centos7安装JDK1.8https://liush.blog.csdn.net/arti…...

为什么北欧的顶级程序员数量远超中国?
说起北欧,很多人会想到寒冷的冬天,漫长的极夜,童话王国和圣诞老人,但是如果我罗列下诞生于北欧的计算机技术,恐怕你会惊掉下巴。Linux:世界上最流行的开源操作系统,最早的内核由Linus Torvalds开…...
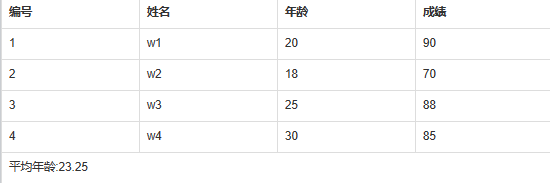
vuex getters的作用和使用(求平均年龄),以及辅助函数mapGetters
getters作用:派生状态数据mapGetters作用:映射getters中的数据使用:方法名自定义,系统自动注入参数:state,每一个方法中必须有return,其return的结果被该方法名所接收。在state中声明数据listst…...
20230311给Ubuntu18.04下的GTX1080M安装驱动
20230311给Ubuntu18.04下的GTX1080M安装驱动 2023/3/11 12:50 2. 安装GTX1080驱动 安装 Nvidia 驱动 367.27 sudo add-apt-repository ppa:graphics-drivers/ppa 第一次运行出现如下的警告: Fresh drivers from upstream, currently shipping Nvidia. ## Curren…...

2023腾讯面试真题:
【腾讯】面试真题: 1、Kafka 是什么?主要应用场景有哪些? Kafka 是一个分布式流式处理平台。这到底是什么意思呢? 流平台具有三个关键功能: 消息队列:发布和订阅消息流,这个功能类似于消息…...
)
23种设计模式-建造者模式(Android应用场景介绍)
什么是建造者模式 建造者模式是一种创建型设计模式,它允许您使用相同的创建过程来生成不同类型和表示的对象。在本文中,我们将深入探讨建造者模式的Java实现,并通过一个例子来解释其工作原理。我们还将探讨如何在Android应用程序中使用建造者…...

English Learning - L2 语音作业打卡 双元音 [ʊə] [eə] Day17 2023.3.9 周四
English Learning - L2 语音作业打卡 双元音 [ʊə] [eə] Day17 2023.3.9 周四💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ʊə…...

【动态规划】多重背包问题,分组背包问题
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

JAVA面向对象特征之——封装
4.封装 private关键字 是一个权限修饰符 可以修饰成员(成员变量和成员方法) 作用是保护成员不被别的类使用,被private修饰的成员只在本类中才能访问 针对private修饰的成员变量,如果需要被其他类使用,提供相应的操作 提供 “get变量名()…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
