高中数学:数列-解数列不等式问题的常用放缩技巧(重难点)
一、放缩技巧
技巧1
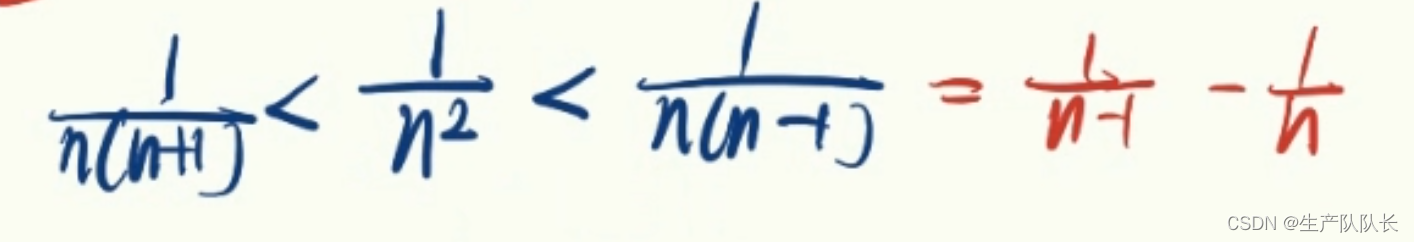
例题
证明:Sn<1

解:

变形
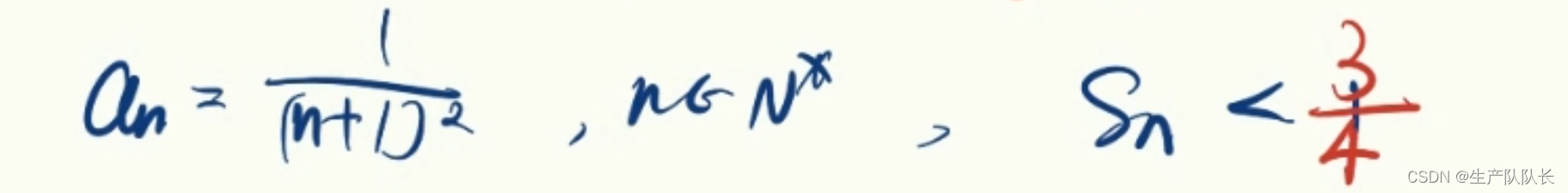
解:
由于第一种情况,我们证明了Sn<1,n≥1,是从第一项就开始放缩的。
发现,无法精确到 3 4 \frac{3}{4} 43
这时,我们就从第二项开始放缩,最终得解。
如果第二项不行,从第三项。以此类推。最终可得解。

总结
本题,我们知道前两项和是
1 4 + 1 9 = 13 36 \frac{1}{4}+\frac{1}{9}=\frac{13}{36} 41+91=3613
那么,我们可以将题目改成
S n < 23 36 S_n<\frac{23}{36} Sn<3623
这个时候,放缩,就要从第三项开始放缩。
技巧2
在1的基础上,提高放缩精确度。
利用平方差公式,进行放缩。
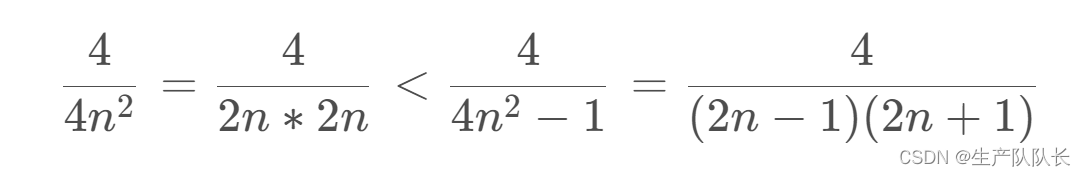
例题
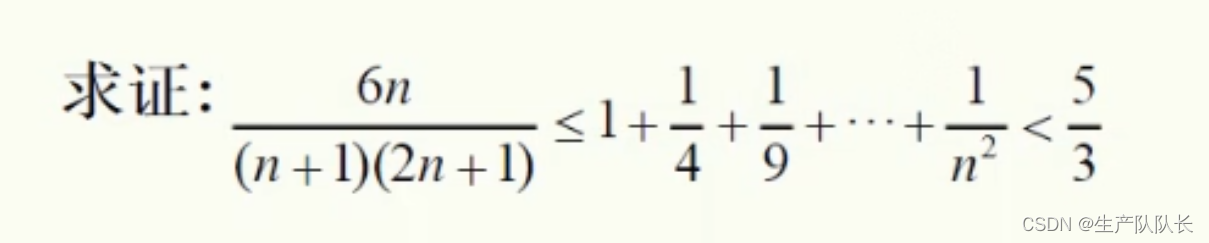
解析:
这里有两个不等号,所以,要证明两次
对于,左边的不等号,我们可以采用技巧1的方式
放缩后,结合二次函数的性质,求出单调性发范围,从而得证
而对于,右边的不等号,我们采用技巧1,就不行了。
分析原因
技巧1中
n 2 > n ∗ ( n − 1 ) = n 2 − n ,可以看出,误差是一个 n 。 n^2>n*(n-1)=n^2-n,可以看出,误差是一个n。 n2>n∗(n−1)=n2−n,可以看出,误差是一个n。
那么,我们如何放缩了?
这里含有一个 n 2 n^2 n2,所以,我们可以想到平方差公式,写成两项乘积的形式
从而,可以使用裂项求和法。
可以这样放缩
4 4 n 2 = 4 2 n ∗ 2 n < 4 4 n 2 − 1 = 4 ( 2 n − 1 ) ( 2 n + 1 ) \frac{4}{4n^2}=\frac{4}{2n*2n}<\frac{4}{4n^2-1}=\frac{4}{(2n-1)(2n+1)} 4n24=2n∗2n4<4n2−14=(2n−1)(2n+1)4
或者
1 n 2 < 1 n 2 − 1 = 1 ( n − 1 ) ( n + 1 ) \frac{1}{n^2}<\frac{1}{n^2-1}=\frac{1}{(n-1)(n+1)} n21<n2−11=(n−1)(n+1)1
这两种放缩方式,都可以解决第二个不等号
放缩技巧都是利用平方差公式
放缩原则:减小误差范围。单项,从误差为n,降到误差为常数C
左边不等号

右边不等号

换放缩方案
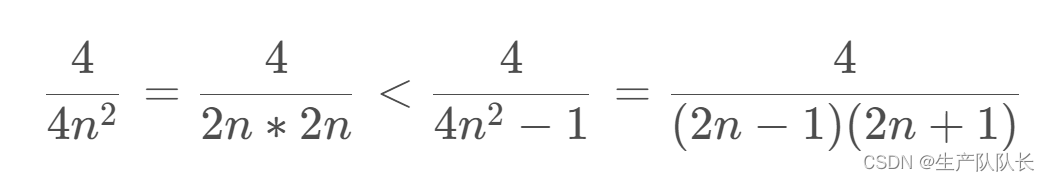
从第二项开始放缩:

总结
上面,我们试了4中放缩方式,现在来说明一下他们之间的精确度
比较他们的大小关系如下:
1 n 2 − n > 1 n 2 − 1 > 4 4 n 2 − 1 > 1 n 2 \frac{1}{n^2-n}>\frac{1}{n^2-1}>\frac{4}{4n^2-1}>\frac{1}{n^2} n2−n1>n2−11>4n2−14>n21
可以发现
4 4 n 2 − 1 \frac{4}{4n^2-1} 4n2−14
距离
1 n 2 \frac{1}{n^2} n21
更近,所以,这个放缩更精确。
以此类推
二、数列不等式放缩原则
1、提高放缩通项公式的精确度。
2、从后几项开始放缩。
相关文章:

高中数学:数列-解数列不等式问题的常用放缩技巧(重难点)
一、放缩技巧 技巧1 例题 证明:Sn<1 解: 变形 解: 由于第一种情况,我们证明了Sn<1,n≥1,是从第一项就开始放缩的。 发现,无法精确到 3 4 \frac{3}{4} 43 这时&am…...
[图解]企业应用架构模式2024新译本讲解17-活动记录1
1 00:00:01,070 --> 00:00:04,180 下一个我们要说的就是 2 00:00:04,190 --> 00:00:06,740 活动记录模式了 3 00:00:07,640 --> 00:00:11,210 同样是数据源架构模式 4 00:00:12,300 --> 00:00:18,480 里面的一个,活动记录 5 00:00:18,490 --> 00…...
[C++深入] --- malloc/free和new/delete
1 new运算符的拓展 1.1 自由存储区与堆的概念 在C++中,内存区分为5个区,分别是堆、栈、自由存储区、全局/静态存储区、常量存储区。 自由存储区是C++基于new操作符的一个抽象概念,凡是通过new操作符进行内存申请,该内存即为自由存储区。 new操作符从自由存储区(free st…...

Spcok测试代码抛异常场景
测试代码抛异常场景 class ExceptionSpec extends Specification {def validateService new ValidateService()Unrolldef "验证UserInfo"() {when: "调用校验方法"validateService.validateUser(user)then: "捕获异常并设置需要验证的异常值&qu…...

【漏洞复现】脸爱云一脸通智慧管理平台 SystemMng 管理用户信息泄露漏洞(XVE-2024-9382)
0x01 产品简介 脸爱云一脸通智慧管理平台是一套功能强大,运行稳定,操作简单方便,用户界面美观,轻松统计数据的一脸通系统。无需安装,只需在后台配置即可在浏览器登录。 功能包括:系统管理中心、人员信息管理中心、设备…...

新手如何入门Web3?
一、什么是Web3? Web3是指下一代互联网,它基于区块链技术,致力于将各种在线活动变得更加安全、透明和去中心化。Web3是一个广义的概念,涵盖了包括数字货币、去中心化应用、智能合约等在内的多个方面。它的主要特点包括去中心化、…...

React.FC`<ChildComponentProps>`解释
代码场景 ParentComponent.tsx import React, { useState } from react; import ChildComponent from ./ChildComponent;function ParentComponent() {const [childData, setChildData] useState<string>();const handleChildData (data: string) > { // 可以直接…...

2024-06-24力扣每日一题
链接: 503. 下一个更大元素 II 题意 循环数组,找出每个元素的往后最近且大于它的元素 解: 今天没试暴力啊,大概率是过不了的 思路就是先找到最大的数,最大数的结果肯定是-1,然后倒着遍历数组…...

pyhon模块以及常用的第三方模块
import my_info as info print(info.name) info.show()from my_info import * print(name) show() pyhon中包的导入 import admin.my_admin as ad # 包名.模块名 admin是包名,my_admin是模块名print(ad.name) print(ad.info())from admin import my_admin as ad # …...

shell脚本—快速修改centos网络配置
shell-文本中自行修改想要的配置 #!/bin/bash# 网卡名称 eth"eth0"# IP 地址 ipaddr"192.168.1.100"# 子网掩码 netmask"255.255.255.0"# 网关 gateway"192.168.1.1"# 写入配置文件 echo "BOOTPROTOstatic" > /etc/sysc…...

线程池概念、线程池的不同创建方式、线程池的拒绝策略
文章目录 💐线程池概念以及什么是工厂模式💐标准库中的线程池💐什么是工厂模式?💐ThreadPoolExecutor💐模拟实现线程池 💐线程池概念以及什么是工厂模式 线程的诞生是因为,频繁的创…...
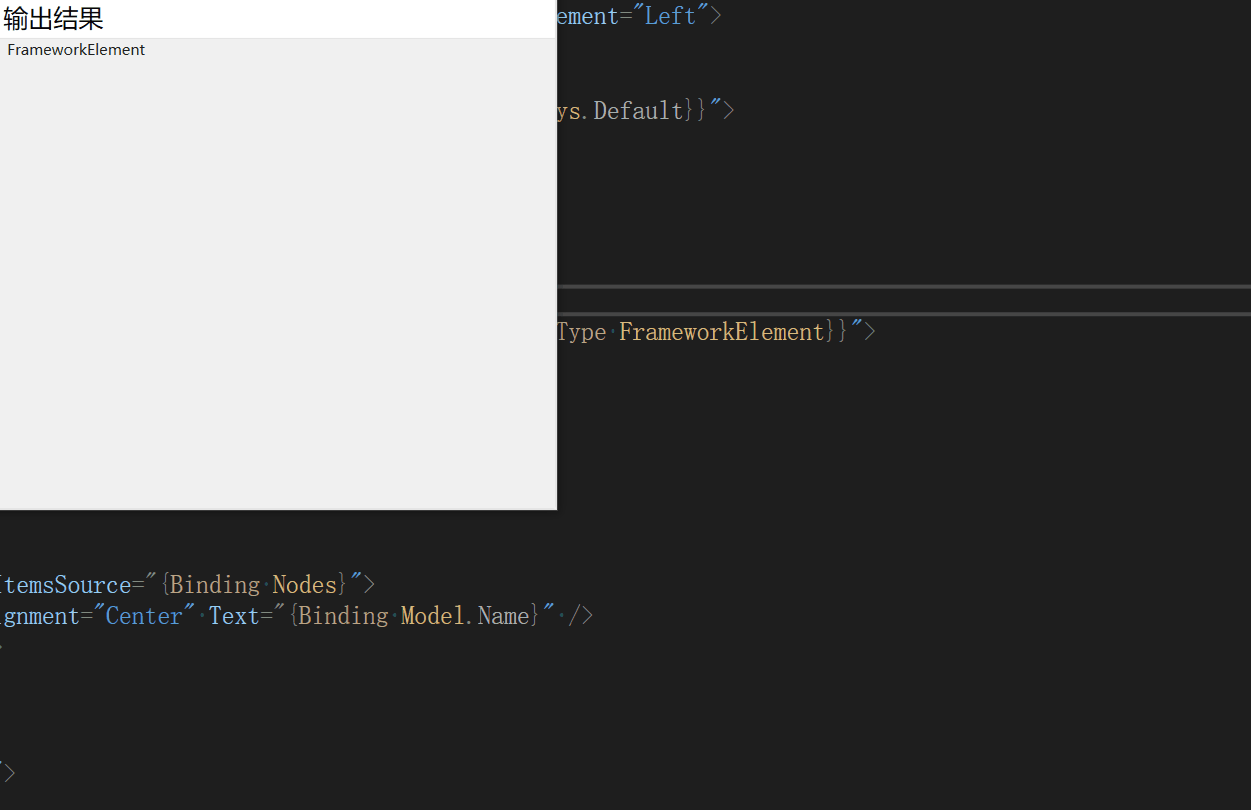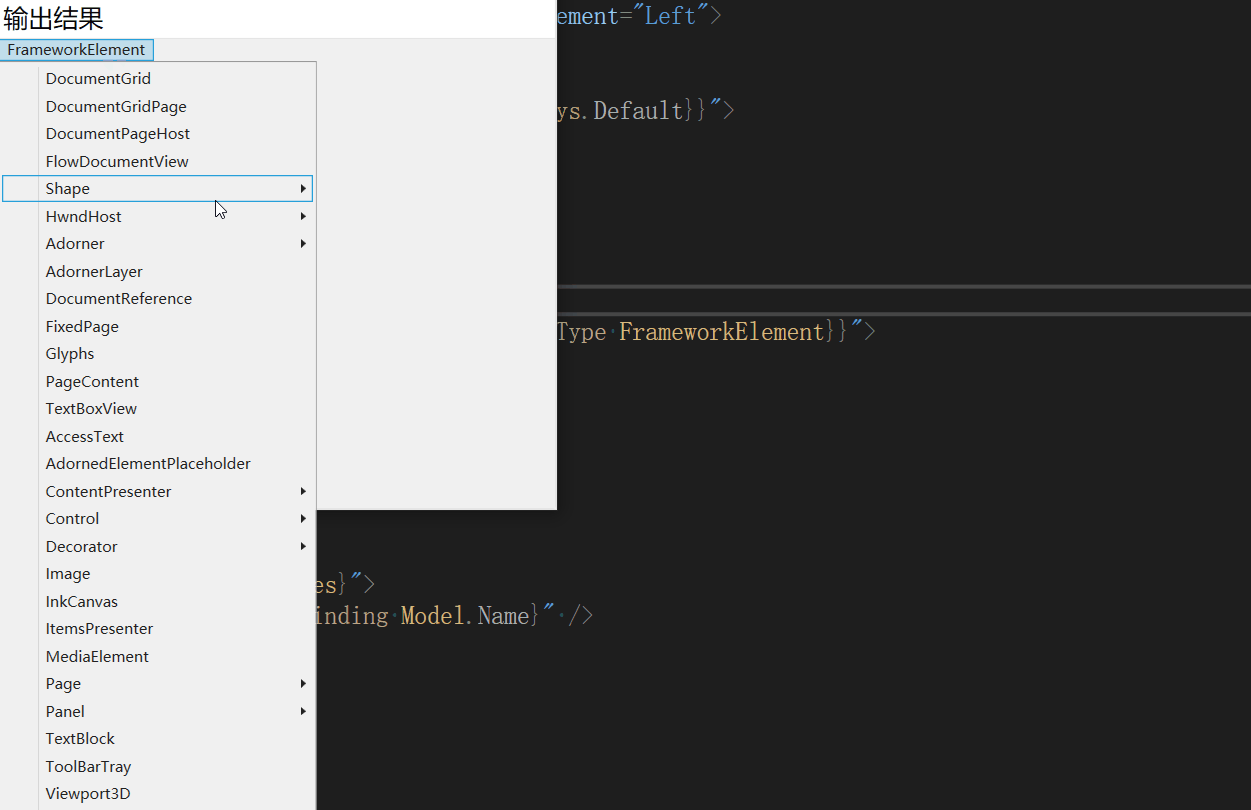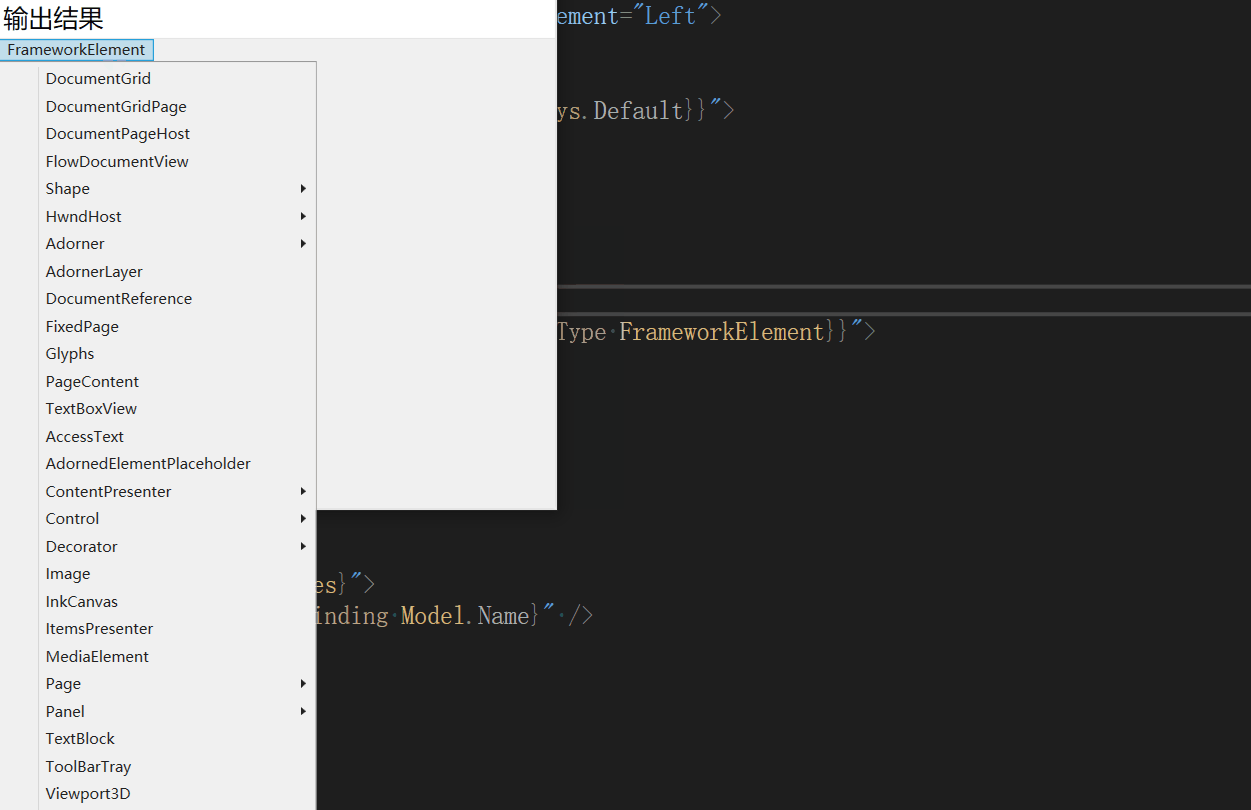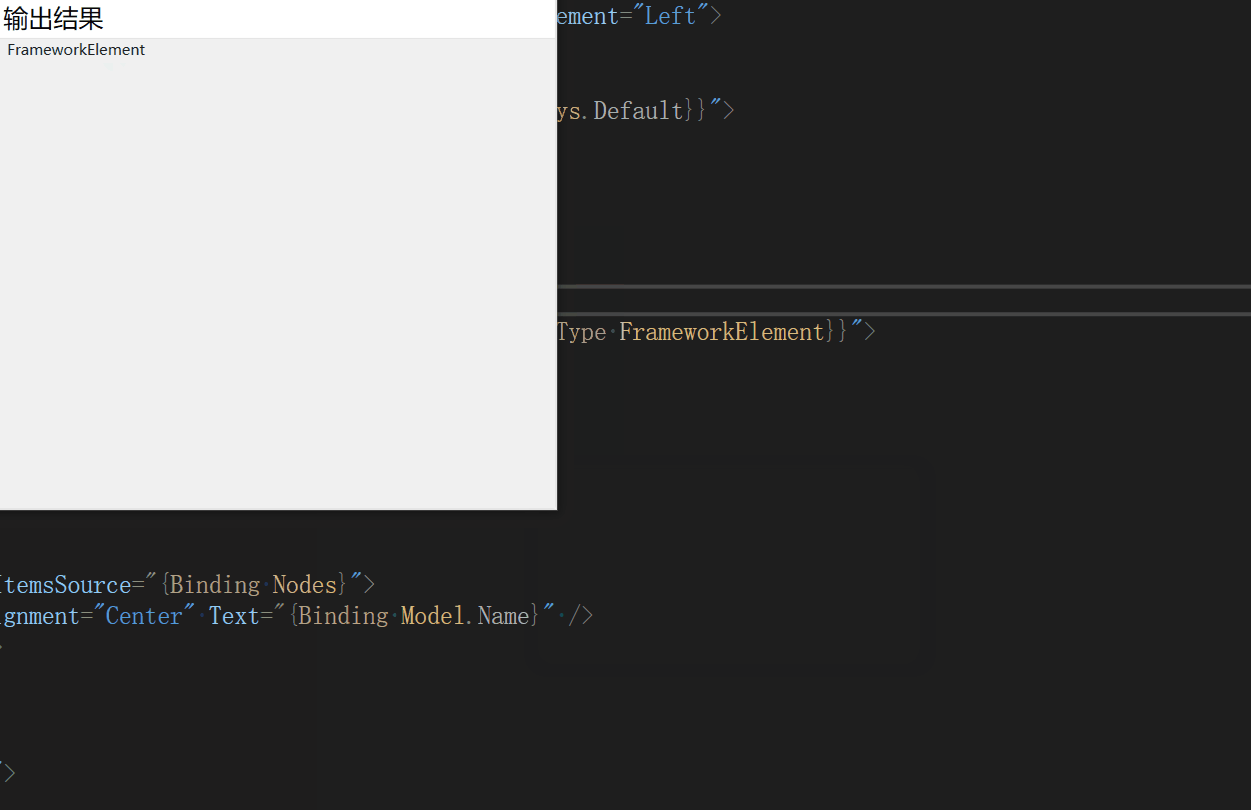
示例:WPF中如何绑定ContextMenu和Menu
一、目的:开发过程中,有些模块的右键ContextMenu菜单是需要动态显示的,既是根据不同条件显示不同的菜单,很多是通过代码去生成ContextMenu的MenuItem,本文介绍通过绑定的方式去加载ContextMenu,Menu菜单栏的…...

区块链小故事
大灰狼与小白兔 一天兔子妈妈出门了,在大门上安装了一个区块链的门把手,这个门把手只有兔子妈妈、小兔子、以及另一个客人都同意的时候,才会开门,有一天客人a的钥匙丢了,被大灰狼捡到了,大灰狼于是去开门&…...

Java | Leetcode Java题解之第167题两数之和II-输入有序数组
题目: 题解: class Solution {public int[] twoSum(int[] numbers, int target) {int low 0, high numbers.length - 1;while (low < high) {int sum numbers[low] numbers[high];if (sum target) {return new int[]{low 1, high 1};} else i…...
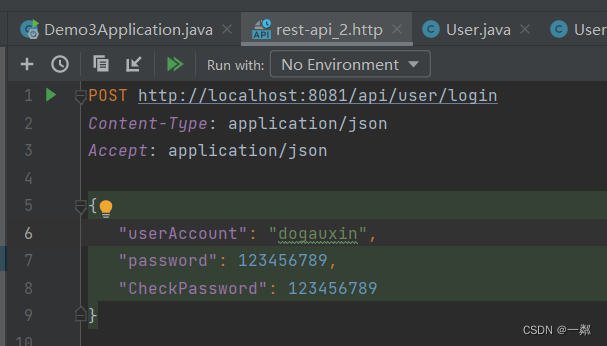
项目训练营第三天
项目训练营第三天 注册登录测试 前面我们编写了用户注册、登录的逻辑代码,每编写完一个功能模块之后,我们都要对该模块进行单元测试,来确保该功能模块的正确性。一般情况下使用快捷键Ctrl Shift Insert,鼠标左击类名可以自动生…...

计算机组成原理 | CPU子系统(1)基本概述
基本结构模型 运算与缓存部件 数据寄存部件 PSW不是很清楚 存储器是什么?属于那个结构里? 时序处理部件 cpu是大脑,控制器是神经元 ①通过硬件产生控制信号 ②通过软件产生控制信号 外频(系统时钟信号),…...

无引擎游戏开发(2):最简游戏框架 | EasyX制作井字棋小游戏I
一、EasyX中的坐标系 不同于数理中的坐标系,EasyX中的y轴是竖直向下的 二、渲染缓冲区 之前的程序添加了这三个函数改善了绘图时闪烁的情况: 小球在"画布“上移动的过程就是我们在调用绘图函数,这个”画布“就是渲染缓冲区,先绘制的内…...

排书 IDA*
原题链接 题目描述 给定 n 本书,编号为 1∼n。 在初始状态下,书是任意排列的。在每一次操作中,可以抽取其中连续的一段,再把这段插入到其他某个位置。我们的目标状态是把书按照 1∼n 的顺序依次排列。求最少需要多少次操作。 输…...
playwright录制脚本原理
Paywright录制工具UI 在上一篇博客中介绍了如何从0构建一款具备录制UI测试的小工具。此篇博客将从源码层面上梳理playwright录制原理。当打开playwright vscode插件时,点击录制按钮,会开启一个新浏览器,如下图所示,在新开浏览器页…...

awk脚本监控
awk脚本监控 使用脚本监控内存,cpu和硬盘的根目录,超过80%提示用户,写成函数库的行,每天早上 的8.50分,执行一次脚本 现在脚本中写需要的内容 cpuu () {aa$(top -b -n 1 |awk NR3 {printf "%.F",$2$4})if …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
